基于刚度退化和纤维单元的RC构件损伤模型

郭宗明+张耀庭+樊剑+卢杰志+罗敏

摘 要：为了评估钢筋混凝土（RC）构件的损伤状态，在Maltab中建立了基于刚度退化和纤维梁柱单元的损伤模型.首先在OpenSees中建立基于纤维梁柱单元的构件、结构数值分析模型，将分析模型所得到的纤维应力、应变值导入在Matlab中所建立的损伤模型，并计算纤维、截面、构件的损伤值.所建立的损伤模型使用再加载刚度退化定义混凝土纤维的损伤，使用低周疲劳准则定义钢筋纤维的损伤，使用塑性应变定义预应力筋的损伤，并分别使用截面抗弯刚度退化、杆端抗弯刚度退化评估截面、构件的损伤.最后，选取循环荷载作用下的一榀预应力混凝土框架结构试验，对所建立损伤模型的适用性进行验证.结果表明：该损伤模型不仅可以准确地预测构件的损伤状态，而且可通过刚度组装和静力凝聚方法在各层次损伤指数间建立紧密的联系.此外，所建立的损伤模型将来可被嵌入OpenSees，直接实现针对混凝土构件和结构的损伤评估.

关键词：刚度退化；纤维梁柱单元；静力凝聚；损伤指数；钢筋混凝土构件

中图分类号：TU375 文献标志码：A

文章编号：1674-2974（2017）03-0076-12DOI：10.16339/j.cnki.hdxbzkb.2017.03.010

Abstract：To estimate the damage state of reinforced concrete （RC） members， a damage model was established based on stiffness degradation and fiber beam-column elements in Matlab. Firstly， the numerical analysis model of a member or a structure based on fiber beam-column elements was established in OpenSees， and the strains and stresses of fibers outputted by OpenSees were then read into the damage model established by Matlab， which estimated the damage values at fiber， section， and member levels. In the established model， fiber damages of concrete， reinforcing steel， and prestressing tendon were defined by the initial reloading modulus degradation， low-cycle fatigue law， and plastic strain， respectively. The section and member damage states were then evaluated by the degradation of the sectional bending stiffness and rod-end bending stiffness， respectively. The established model was verified by comparison with a structural test results of prestressed concrete frame subjected to cyclic loads. The results indicate that the damage model can determine its damage states accurately， and a close relationship between damage indices at various levels by using the direct stiffness method and static condensation method. Furthermore， the established damage model can be embedded in OpenSees to determine the damage states of RC members and structures directly in the future.

Key words：stiffness degradation； fiber beam-column element； static condensation； damage index； reinforced concrete member

作為基于性能地震工程的重要研究内容之一，结构的损伤评估已成为土木工程领域的热门研究课题.近几十年来，多种适用于钢筋混凝土构件、结构的损伤模型[1-5]相继被提出.损伤模型通常使用损伤指数对损伤程度进行量化，并被表示为某个或多个特定反应参数的函数，这些反应参数包括：应力、位移、延性、刚度、滞回能等.

作为损伤模型常用的参数之一，刚度可以直接描述材料、截面、构件和结构的力学性能.因此，基于刚度退化的损伤模型可用于评估上述各层次的损伤状态.不同的研究者已基于刚度退化提出可用于评估构件、结构损伤状态的损伤模型.Ghobarah等[6]根据地震前后力位移曲线初始斜率的变化评估楼层、结构的损伤； Kunnath等[7]使用割线刚度及加载前的切线刚度建立了适用于构件和结构的损伤模型.目前基于刚度退化的损伤模型大多假设损伤集中在构件的某些特定区域，并通过引入塑性铰或其他类型的铰体现上述假设.但由于地震作用及结构本身具有随机性，造成损伤出现的位置带有一定的随机性.因此，这些损伤模型很难准确地识别出损伤的具体位置及大小，甚至对构件局部的损伤造成误判.与集中损伤假设不同，纤维梁柱单元假设非弹性行为分布于整个单元，因此将纤维梁柱单元引入构件和结构的损伤分析有望解决上述问题.

在基于纤维单元的损伤模型中，纤维损伤指数的定义是该方法的基础，而如何建立各层次损伤指数的联系则是该方法的关键.Tsuchiya等[8]使用断裂系数定义混凝土的损伤，使用截面的平均断裂系数定义截面损伤.Teng等[9]和Li等[10]使用最不利截面的平均损伤指数定义截面损伤.Heo[11]通过混凝土的应力值定义其损伤指数，通过钢筋的低周疲劳寿命定义其损伤指数，之后使用加权系数方法得到了构件、结构的损伤.李忠献等[12]基于刚度退化和自由能退化线性组合评估钢筋混凝土构件的损伤.虽然上述损伤模型都引入了纤维单元计算各层次的损伤，但由于加权系数、平均值等方法的频繁使用，不仅破坏了损伤指数与其物理意义的联系，也在损伤转化过程中引入了更多的不确定性.

为解决现有基于刚度退化的损伤模型和基于纤维单元的损伤模型所存在的不足，本文联合使用刚度退化和纤维单元建立了新的损伤模型.同时，在各层次损伤指数的转化过程中，使用了直接刚度法和静力凝聚法.最后，选取循环荷载作用下的一榀预应力混凝土框架，对所建立的损伤模型进行验证，以确定所建立模型的可靠性并评估其损伤状态.

1 基于刚度退化和纤维单元损伤模型的建立

本文使用Simplified Chang and Mander Concrete模型[2， 13]、Modified Reinforcing Steel模型[14]和Hysteretic模型[14]分别描述混凝土、普通钢筋和预应力筋的力学行为.如图1所示，首先使用OpenSees对结构进行受力分析，使用“recorder”命令输出纤维的应力、应变.使用Matlab的“load”命令读入纤维的应力、应变等数据，并通过在Matlab中建立的损伤模型计算纤维、截面、构件等层次的损伤.其中，混凝土纤维使用再加载刚度的退化定义其损伤指数，钢筋纤维使用低周疲劳准则定义其损伤指数，预应力筋使用塑性应变定义其损伤指数.之后，通过计算包含损伤纤维贡献的截面抗弯刚度的退化定义截面的损伤.然后使用基于力的方法将截面有效刚度矩阵转化为单元有效刚度矩阵，使用直接刚度方法和静力凝聚方法将单元有效刚度矩阵转化为只包含杆端自由度的构件有效刚度矩阵，通过杆端抗弯刚度的退化定义单个构件的损伤指数.

若单根构件只使用一个单元进行模拟，则式（19）经坐标转换后可直接用于描述具有刚体位移模式的杆端力与杆端位移的关系.若单根构件使用若干单元进行模拟，则将所有单元有效刚度矩阵组装成具有刚体位移模式的构件有效刚度矩阵，使用静力凝聚法去除内部节点的自由度.对于上述2种情况（如图5所示），单根构件杆端力Fmember与杆端变形dmember的关系都可以表示为：

2 损伤模型的验证

本文选取由孟少平[24]进行拟静力测试的一榀2层2跨预应力混凝土框架对所建立的损伤模型进行说明和验证.框架编号为PPCF-2，为保证节点不发生剪切破坏，在内节点梁下加腋，其尺寸与配筋如图6所示.测试过程中，恒定竖向荷载80 kN首先加在各梁的跨中，之后水平往复荷载作用在预应力框架的各楼层上.水平荷载由力位移混合方法控制（如图7所示），水平力在第一层、第二层的加载比例为1∶2.2.

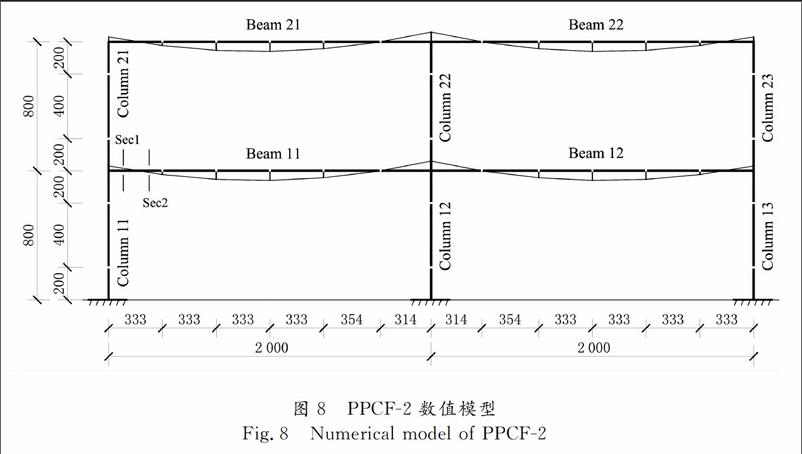
预应力混凝土梁数值分析模型由钢筋混凝土梁、预应力筋和连接键组成.每根钢筋混凝土梁被划分为6个单元，每个梁单元包含4个Gauss-Lobatto积分点.使用6段直线线型拟合预应力筋曲线线型，并使用Hysteretic模型模拟预应力筋的滞回性能，预应力筋的有效预应力值为839 N/ mm2.连接键为刚臂连接，以实现预应力筋结点与钢筋混凝土梁相应结点的自由度耦合.预应力构件的建模细节见文献[25].每根钢筋混凝土柱被划分为3个单元，每个柱单元包含5个Gauss-Lobatto积分点.梁、柱编号如图8所示.钢筋混凝土梁截面被划分为6×10根纤维（图9（a）），钢筋混凝土柱截面被划分为10×10根纤维（图9（b））.混凝土和钢筋的本构被定义在纤维上.选用Concrete07材料模型，即Simplified Chang and Mander模型，模拟约束和非约束混凝土纤维的滞回性能.选用Modified Reinforcing Steel材料模型模拟钢筋的滞回行为.数值仿真模型中，钢筋与混凝土所采用的力学参数见表1.预应力混凝土框架基底剪力顶层位移的实验结果和模拟结果如图10所示，结果表明模拟与实验吻合得较好，因此所建立的纤维分析模型可用于评估预应力混凝土框架的损伤.

使用所建立的损伤模型可以观察到混凝土纤维的损伤发展过程.选取梁Beam 11最左侧单元中的第2个截面Sec1（图8）中的混凝土纤维C1，C2和C3的受压损伤说明这一发展过程（如图11所示）.由于C2更靠近梁的外侧，所以与C1（如图12 （a）所示）相比C2所经受的压应变更大（如图12 （b）所示），C1的损伤指数值要比C2大.对于局部y坐标值相同的C2和C3，由于侧向约束效应的影响，C2的应力应变性能得到改善（如图12 （b）（c）所示），C3的损伤指数值比C2大.

选取梁Beam 11最左侧单元中的第2个截面Sec1和第3个截面Sec2 （图8）中局部坐标相同的钢筋纤维Rs，分别记为Rs1和Rs2，观察其损伤发展过程（图13）.由于Rs1更靠近梁端，所经历的应变幅值更大（图14），所以Rs1的损伤值比Rs2大.

选取梁Beam 11最左侧单元中的第2个截面Sec1 （图8）中的预应力钢筋纤维Pt（记为Pt1）说明其损伤发展过程（图15）.从图16可以看出，预应力筋Pt1经历了塑性應变，其最大应变值为0.012 6（图16），最大损伤值达到0.123 4.

在恒定竖向荷载作用下，预应力混凝土框架PPCF-2经历了31次水平加载循环.选取其中的7个加载点（如图17所示），说明PPCF-2梁柱各截面的损伤发展过程.跨中竖向荷载加载至80 kN后（加载点 A），各层梁的跨中、两端出现23条弯曲裂缝，如图17（a）所示各层梁的跨中、两端出现了明显的损伤.第3个水平加载循环结束后（加载点B），上、下各层梁端均出现竖向弯曲裂缝，如图17（b）所示各层梁两端的损伤发展比较迅速.第5个水平加载循环结束后（加载点C），Beam 11 和 Beam 21左侧出现少量新的正弯曲裂缝、已有裂缝进一步延伸，此时Beam 11 和 Beam 21左侧的损伤有了明显的发展（如图17（c）所示），两根梁截面的最大损伤值分别达到0.581 0和0.615 4.该加载步结束时，Column 22 的两端出现了水平裂缝，Column 23 的顶端出现微裂缝，这些现象与图17（c）相吻合.从第5个加载循环结束至第14个加载循环结束（加载点C→加载点E）的过程中，梁端已有弯曲裂缝不断延伸，Beam 11和Beam 21左端与Beam 12和Beam 22右端的非预应力筋屈服，柱底出现水平裂缝且中柱开始出铰.此过程中，预应力框架的损伤发展与图17（d）（e）一致.之后，梁端与柱端的塑性铰进一步发展，至第25个水平加载循环结束后（加载点F），梁端塑性铰截面保护层混凝土被压碎，底层柱根部混凝土被局部压酥，这些现象与图17（f）相吻合.整个加载结束时，梁端塑性铰已经历较大转动，裂缝开展明显，底层柱根部混凝土局部剥落（如图18所示），最终破坏形态与图17（g）一致.

通过分析各层构件的损伤发展过程（如图19所示），可以发现：整个加载过程中，梁的损伤指数值大于边柱的损伤指数值；加载结束时，一层边柱、中柱的损伤指数值与梁的损伤指数值比较接近，二层中柱的损伤指数值与梁的损伤指数值比较接近，边柱损伤指数值较小.以上结果与预应力框架PPCF-2预期破坏形态相符（如图18所示），也与其“混合耗能”设计准则相符，即：边节点采用“强柱弱梁”设计，内节点采用“强梁弱柱”设计.说明所建立的损伤模型可以准确预测构件的损伤状态，并可用于确定结构的失效路径及预测结构的失效模式.

3 结 论

为了实时、准确地确定钢筋混凝土构件的损伤状态，本文基于刚度退化和纤维单元，利用OpenSees得到的加载过程中材料的应力、应变数值，在Maltab中建立了一个适用于钢筋混凝土构件的损伤模型.将所建立的损伤模型应用于循环荷载作用下的一榀预应力钢筋混凝土框架结构试验的分析，以对该模型进行验证.基于本文研究，可得到如下结论：

1）预应力混凝土框架的损伤计算结果表明，所建立的损伤模型可以准确确定混凝土、钢筋和预应力筋的损伤值，并确定截面、构件的损伤位置、损伤状态，并据此确定结构的失效路径、预测结构的失效模式.

2）由于本文所提出的损伤模型将纤维的刚度退化和有效面积作为计算的基础，在不引入截面、构件层次力位移关系的条件下，即可评估截面、构件的损伤， 因此，所提出的模型可以不引入加权系数，而利用有限元中的方法（直接刚度法、静力凝聚法）准确地确定各层次的损伤，减少了各层次损伤指数在转化过程中的不确定性.

3）静力凝聚法不仅减少了计算自由度、考虑了内部损伤的影响，为直接刚度法的使用提供了便利，也为损伤模型的简便、定量地实验验证提供了理论依据.

该模型完善了OpenSees中针对构件的损伤评估功能，为地震作用下大型结构多层次损伤评估打下了坚实基础.然而，该模型还存在一些局限性.如：没有考虑混凝土受压损伤和受拉损伤之间的相互影响，未考虑纵向钢筋的非弹性屈曲效应，也未考虑预应力筋低周疲劳损伤.除了应优化混凝土、钢筋及预应力筋的损伤模型，未来的研究也应确定楼层、结构的损伤指数及不同损伤等级所对应的损伤指数范围，为所建立的损伤模型应用于构件及结构的损伤评估提供依据.

参考文献

[1] PARK Y， ANG A. Mechanistic seismic damage model for reinforced concrete[J]. Journal of Structural Engineering， 1985， 111（4）： 722-739.

[2] MANDER J B， CHENG C. Renewable hinge detailing for bridge columns [C]//Proceedings of Pacific Conference on Earthquake Engineering. Melbourne， Australia： Australian Earthquake Engineering Society， 1995： 197-206.

[3] GHOBARAH A. Performance-based design in earthquake engineering： state of development[J]. Engineering Structures， 2001， 23（8）： 878-884.

[4] 陈清军，周成杰，楊永胜. 基于环境振动信号的框架结构震后损伤识别[J]. 湖南大学学报：自然科学版， 2014， 41（9）： 20-26.

CHEN Qingjun， ZHOU Chengjie， YANG Yongsheng. Damage identification of frame structure after earthquakes based on environmental vibration records[J].Journal of Hunan University：Natural Sciences， 2014， 41（9）： 20-26. （In Chinese）

[5] YAZGAN U， DAZIO A. Post-earthquake damage assessment using residual displacements[J]. Earthquake Engineering & Structural Dynamics， 2012， 41（8）： 1257-1276.

[6] GHOBARAH A， ABOU-ELFATH H， BIDDAH A. Response-based damage assessment of structures[J]. Earthquake Engineering & Structural Dynamics， 1999， 28（1）： 79-104.

[7] KUNNATH S K， EL-BAHY A， TAYLOR A W， et al. Cumulative seismic damage of reinforced concrete bridge piers[R]. Buffalo， NY： US National Center for Earthquake Engineering Research， 1997： 111-128.

[8] TSUCHIYA S， MAEKAWA K. Cross-sectional damage index for RC beam-column members subjected to multi-axial flexure[J]. Journal of Advanced Concrete Technology， 2006， 4（1）： 179-192.

[9] TENG J， LI Z， OU J， et al. Fiber damage analysis model for RC beam-column based on EEP super-convergent computation[J]. Science China Technological Sciences， 2011， 54（10）： 2542-2548.

[10]LI Z， TENG J， HE X. Seismic damage analysis model for RC structures based on concrete plastic damage model [C]//Proceedings of Structures Congress 2011. Las Vegas， Nevada： American Society of Civil Engineers， 2011： 2768-2779.

[11]HEO Y. Framework for damage-based probabilistic seismic performance evaluation of reinforced concrete frames[D]. Ann Arbor： University of California， Davis， 2009： 92-119.

[12]李忠献，陈宇，李宁. 基于材料损伤的钢筋混凝土构件损伤模型[J]. 工程力学， 2014， 31（6）： 53-59.

LI Zhongxian ， CHEN Yu ， LI Ning. A damage model for reinforced concrete members based on material damage[J]. Engineering Mechanics， 2014，31（6）： 53-59. （In Chinese）

[13]WAUGH J D. Nonlinear analysis of T-shaped concrete walls subjected to multi-directional displacements[D]. Ames， Iowa： Department of Civil， Construction， and Environmental Engineering， Iowa State University， 2011： 36-67.

[14]MAZZONI S， MCKENNA F， SCOTT M H， et al. OpenSees command language manual[R]. Berkeley， California： Pacific Earthquake Engineering Research Center， 2006： 131-147.

[15]KOH S K， STEPHENS R I. Mean stress effects on low cycle fatigue for a high strength steel[J]. Fatigue & Fracture of Engineering Materials & Structures， 1991， 14（4）： 413-428.

[16]MINER M A. Cumulative damage in fatigue[J]. Journal of Applied Mechanics， 1945， 12： A159-A164.

[17]張耀庭，赵璧归，杜晓菊，等. 基于纤维模型的 RC 结构的钢筋本构关系研究[J]. 湖南大学学报：自然科学版， 2015，42（9）： 23-32.

ZHANG Yaoting， ZHAO Bigui， DU Xiaoju， et al. Research on the constitutive model of steel for reinforced concrete structures based on the fiber model[J].Journal of Hunan University： Natural Sciences， 2015，42（9）： 23-32. （In Chinese）

[18]DODD L， RESTREPO-POSADA J. Model for predicting cyclic behavior of reinforcing steel[J]. Journal of Structural Engineering， 1995， 121（3）： 433-445.

[19]MANSOUR M， LEE J， HSU T T. Cyclic stress-strain curves of concrete and steel bars in membrane elements[J]. Journal of Structural Engineering， 2001， 127（12）： 1402-1411.

[20]HSU T T， MO Y. Unified theory of concrete structures[M]. Chichester， United Kingdom： John Wiley & Sons， 2010： 381-410.

[21]VAN PAEPEGEM W， DECHAENE R， DEGRIECK J. Nonlinear correction to the bending stiffness of a damaged composite beam[J]. Composite Structures， 2005， 67（3）： 359-364.

[22]LI S， ZHAI C， XIE L. Evaluation of displacement-based， force-based and plastic hinge elements for structural non-linear static analysis[J]. Advances in Structural Engineering， 2012， 15（3）： 477-488.

[23]WELFERT B D. A note on classical Gauss-Radau and Gauss-Lobatto quadratures[J]. Applied Numerical Mathematics， 2010， 60（6）： 637-644.

[24]孟少平. 預应力混凝土框架结构抗震能力及设计方法的研究[D]. 南京：东南大学土木工程学院， 2000：74-89.

MENG Shaoping. Study on capacity and design approach of prestressed concrete frame structures for seismic resistance [D]. Nanjing： School of Civil Engineering， Southeast University， 2000： 74-89. （In Chinese）

[25]郭宗明，张耀庭，卢杰志，等. 基于纤维单元的预应力混凝土构件非线性有限元分析模型研究[C]//第24届全国结构工程学术会议论文集. 北京： 中国力学学会， 2015： I368-I376.

GUO Zongming， ZHANG Yaoting， LU Jiezhi， et al. A study on the nonlinear finite element analytical model for prestressed concrete members based on OpenSees [C] //Proceeding of the 24th National Conference on Structural Engineering. Beijing： The Chinese Society of Theoretical and Applied Mechanics， 2015： I368-I376.