焊肉位置对连续管冲蚀磨损规律研究*

吴　晗，刘少胡，刘旭辉，周传喜，金　高，魏世忠

(长江大学 机械工程学院，湖北 荆州 434023)

0　引言

在压裂过程中，压裂液以足够高的速率来克服地层中岩石的抗拉强度从而将地层压裂开，同时，还需要持续不断地泵送压裂液来扩展地层裂缝[1]。压裂液在高压高速的泵送过程中，容易引起连续管的冲蚀磨损甚至失效。

目前国内外学者对连续管及冲蚀磨损进行了较为深入的研究。S. N. Shah等[1-2]利用实物试验和CFD仿真研究了流速、泥浆浓度、支撑剂大小和密度以及流体黏度对卷筒上连续管冲蚀磨损速率的敏感度；R.S. Rosine，M. Bailey等[3-5]对比了现场实际数据与CFD的计算结果，验证了CFD技术研究连续管冲蚀的可靠性；鄢标等[6]采用控制变量法分别研究了支撑剂质量浓度、携砂液流量以及支撑剂粒径对螺旋段油管冲蚀磨损率的影响；刘少胡等[7]研究了弯曲连续管与直连续管、质量流量、砂砾粒度、压裂液注入排量及压裂液黏度对连续管外壁冲蚀磨损规律影响；郑华林等[8]研究了连续管在不同弯曲度下连续管内壁的冲蚀特性。

综上，现有研究主要是分析不同因素对连续管冲蚀磨损大小的影响，但是在对连续管进行建模过程中，忽略了连续管焊肉的存在，这将导致数值计算结果偏离实际情况，而针对焊肉对连续管冲蚀磨损影响的研究尚未见报道。基于此，利用CFD技术，结合FLUENT软件研究了直连续管、360°弯曲连续管、正弦弯曲连续管等连续管焊肉对连续管内壁冲蚀磨损，以及焊肉位置对360°弯曲连续管的冲蚀磨损规律。

1　连续管内部焊肉

在连续管焊接过程中，母材被熔化形成焊肉，连续管中的焊肉如图1所示。表征焊肉形状的参数主要有焊宽和余高，如图2所示。焊宽即焊缝2焊趾之间的距离；余高指超出母材表面连线上的那部分焊缝金属的最大高度[9]。以下以内径为30.2 mm、外径为38.1 mm且焊肉形状为椭圆形(焊宽为3 mm，余高为2.5 mm)的连续管为研究对象[1,10]。

图1　 连续管焊肉[11]Fig.1　CT weldment

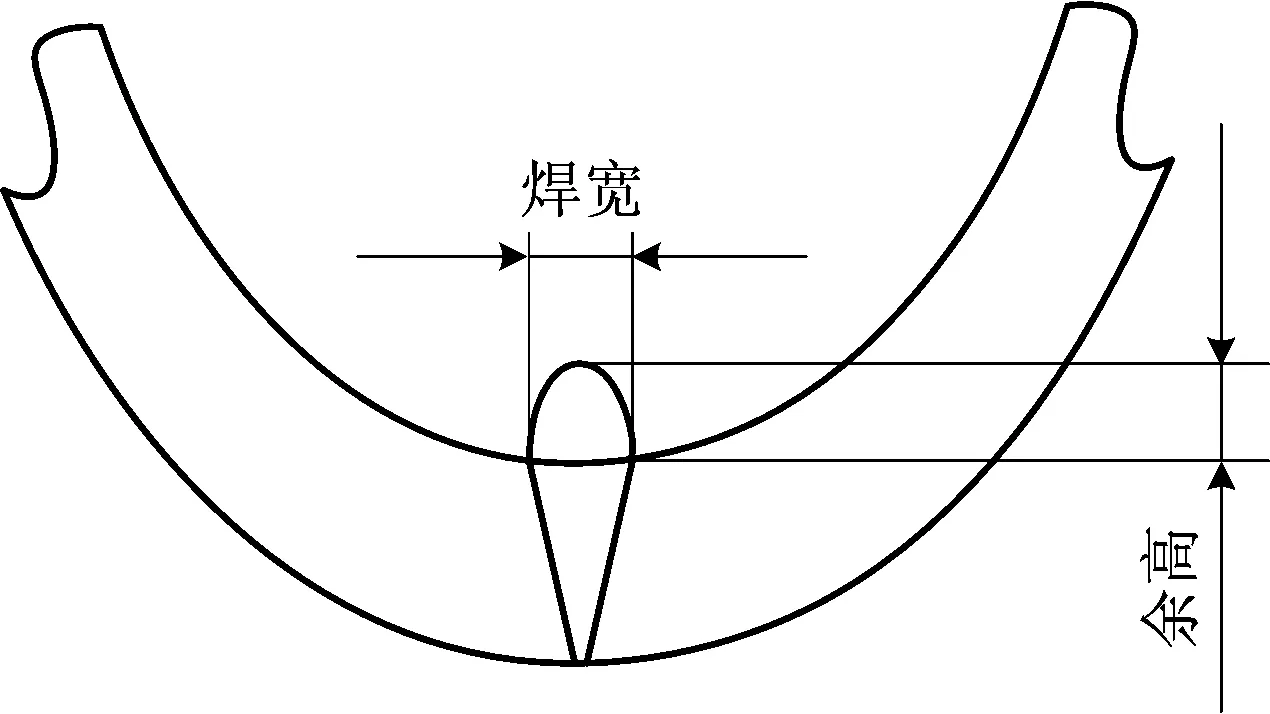
图2　 连续管焊肉形状参数Fig.2　Shape parameters of CT weldment

2　三维紊流流场数值模拟

由于压裂液含有支撑剂颗粒，因此在压裂过程中弯曲连续管作业时内部流体是复杂的液-固两相三维紊流流场。根据离散相模型，连续相为液相，离散相为支撑剂颗粒，在拉格朗日坐标系下求解粒子相的运动方程，离散相轨道模型可以完整的考虑颗粒与液体间的耦合作用。连续管三维紊流流场模拟采用标准k-ε两方程模型使方程组闭合[12]。

2.1　控制方程

1)质量守恒方程

(1)

2)动量守恒方程

(2)

3)标准k-ε两方程模型

(3)

(4)

式中：ρ为密度，kg/m3；u为流体速度矢量，m/s；p为压力，Pa；μt为湍流粘性系数，kg/(m·s)；ε为耗散率，m2/s3；k为湍流动能，m2/s2。

4)离散颗粒的力平衡方程

离散颗粒的力平衡方程为颗粒惯性作用在颗粒上的各种力，可表示为：

(5)

式中：FD(u-up)为颗粒的单位质量曳力。

2.2　连续管内壁冲蚀模型

连续管内壁的冲蚀速率定义为单位时间内由于冲蚀引起材料质量的减少量[13]，即：

(6)

式中：mp为颗粒质量流量，kg/s；f(α)为冲击角α的函数；v0为冲击速度，m/s；n为冲击速度指数；c(dp)为颗粒直径的函数；Aface为冲蚀面积，m2。

2.3　网格划分及边界条件

为了更好地模拟管壁处的冲蚀磨损情况，流道模型采用六面体网格划分，在管壁处进行网格加密处理，对焊肉壁面进行了局部网格细化。

参照文献[6]，连续管进口处设置为速度进口边界，出口设置为自由出口，壁面采用标准壁面函数处理。进口处颗粒速度与液相速度均为13.26 m/s，颗粒直径为0.691 mm，颗粒质量流量[1]为4.550 5 kg/s。动量、能量、湍动能和湍流耗散率的离散均采用二阶迎风格式，压力速度耦合采用Simple算法。

3　影响弯曲连续管内壁冲蚀磨损因素分析

根据连续管的工作特性，连续管的形状主要有竖直状、缠绕在卷筒上的圆周曲线状以及井下作业时的正弦曲线状[14-16]，为了研究连续管在不同形状下的冲蚀磨损情况，下文在考虑焊肉的情况下选取了这3种形状进行对比分析。由于连续管的弯曲变形，焊肉在连续管内部的位置也不同，因此以下结合360°弯曲连续管，研究焊肉在不同位置时对连续管的冲蚀情况。

3.1　弯直连续管冲蚀磨损对比

在直径为1 830 mm的滚筒上缠绕内径为30.2 mm的连续管进行压裂作业，结合以上数据，采用360°弯曲连续管、解析公式为y=30 sin(0.03x)的正弦弯曲连续管以及直连续管进行对比分析，直连续管、360°弯曲连续管以及正弦弯曲连续管的冲蚀云图如图3所示。

图3　 连续管冲蚀速率Fig.3　Contours of DPM erosion rate of CT

对比直管、360°弯曲管以及正弦弯曲管的冲蚀云图，3种情况下的连续管内壁冲蚀规律区别明显。由图4可见，360°弯曲连续管的最大冲蚀速率为7.33×10-4kg·m-2·s-1，较直连续管最大冲蚀速率(3.17×10-5kg·m-2·s-1)增加了近22倍，正弦弯曲连续管的最大冲蚀速率为8.39×10-3kg·m-2·s-1，较直连续管最大冲蚀速率增加了近264倍，因此正弦弯曲连续管的最大冲蚀速率最大，直连续管最大冲蚀速率最小。分析认为：正弦弯曲连续管中进口处拐弯段的曲率半径相对于360°弯曲连续管较小，导致压裂液流动方向急剧改变，在离心力的作用下，离散颗粒主要集中在连续管外侧[17](如图5)，从而导致颗粒对连续管内壁的碰撞加剧，因此冲蚀磨损最为严重；而直连续管中颗粒不受离心力作用，颗粒对连续管管壁碰撞程度较小，因此冲蚀磨损最小。

图4　 连续管冲蚀速率对比Fig.4　A comparison of CT erosion rate

图5　 连续管滑动磨损示意Fig.5　Schematic of sliding erosion in CT

3.2　焊肉位置分布对弯曲连续管冲蚀影响

3.2.1焊肉分布在同一侧时对弯曲连续管冲蚀影响

连续管缠绕在滚筒上时，其内部焊肉的位置会出现多种情况。为了研究焊肉的不同位置对连续管冲蚀的影响，选取了焊肉的4个分布位置，且建立了360°弯曲连续管不同的焊肉位置分布时的三维流道模型，如图6所示。

图6　 不同焊肉位置分布的360°弯曲连续管流道模型Fig.6　Flow field model of CT with weldment in different positions

从图7可知，当焊肉分布在360°弯曲连续管外侧时，连续管所受的最大冲蚀速率最大，为7.33×10-4kg·m-2·s-1，较无焊肉时的最大冲蚀速率(4.68×10-4kg·m-2·s-1)增加了约57%；焊肉分布在内侧、左侧和右侧时，其最大冲蚀速率与无焊肉的最大冲蚀速率基本相同。其原因在于，压裂液在泵送过程中，由于离心力的作用导致压裂液中的离散颗粒集中在弯曲连续管外侧位置，因而外侧所受到的碰撞磨损较大，当焊肉分布在外侧时，使得压裂液沿外侧的流动更为复杂，颗粒碰撞次数增多，所以最大冲蚀速率最大。

图7　无焊肉与不同焊肉位置的冲蚀速率对比Fig.7　A comparison of erosion rate between no-weldment and weldment in different positions

3.2.2焊肉呈螺旋分布时对弯曲连续管冲蚀影响

连续管在使用过程中，经过反复的下放与回收使得连续管发生扭转变形，从而使缠绕在滚筒上的弯曲连续管焊肉不再是沿一侧分布，而是呈螺旋式分布(见图8)，以下结合油田现场连续管的实际使用情况，选取焊肉扭转角度范围为90～360°的360°弯曲连续管进行研究，如图9所示，随着扭转角度的增大，最大冲蚀速率呈递增趋势，由90°时的9.25×10-4kg·m-2·s-1增加了277%，达到360°时的3.49×10-3kg·m-2·s-1，而平均冲蚀速率在2.7～2.3×10-5kg·m-2·s-1之间呈递减趋势。其原因在于，螺旋式分布的弯曲连续管焊肉使得压裂液在流动过程中产生涡流现象，焊肉扭转角度越大，涡流现象越明显，弯曲连续管受固体颗粒的冲蚀磨损越严重。

图8　螺旋式焊肉分布弯曲连续管流场模型Fig.8　Flow field model of CT with auger-type weldment

图9　焊肉不同扭转角度的冲蚀速率规律Fig.9　Rule of erosion rate with weldment in different twist angle

4　结论与建议

1)通过对比研究得出，直连续管、360°弯曲连续管和正弦弯曲连续管等3种连续管中，直连续管冲蚀磨损最小，360°弯曲连续管的最大冲蚀速率较直连续管增加了近22倍，正弦弯曲连续管的最大冲蚀速率较直连续管增加了近264倍，且正弦弯曲连续管的进口段拐弯处的冲蚀最为严重。

2)在360°弯曲连续管中，当焊肉分布在外侧时连续管所受的最大冲蚀速率较无焊肉增加了约57%；焊肉在连续管内的扭转角度由90°增加到360°时，连续管最大冲蚀速率增加了约277%。建议卷筒上缠绕连续管时尽量控制焊肉位于内侧位置，同时控制焊肉的扭转变形以减小冲蚀磨损。

[1]Subhash N. Shah, Samyak Jain. Coiled tubing erosion during hydraulic fracturing slurry flow[J]. Wear, 2008(264):279-290.

[2]S.N. Shah, S. Jain, Y. Zhou. Coiled Tubing Erosion During Hydraulic Fracturing Slurry Flow[R]. SPE 89479, 2004.

[3]M. Bailey, I.L. Blanco, R.S. Rosine. Comparison of Computational Fluid Dynamics of Erosion in Coiled Tubing on Reel-to-Injector Flow Area[R], SPE 121171, 2009.

[4]R.S. Rosine, I.L. Blanco, M. Bailey. Comparison of Computational Fluid Dynamics of Erosion in Coiled Tubing to Field and Test Data[R]. SPE 113619, 2008.

[5]I.L. Blanco, R.S. Rosine, M. Bailey. Comparison of Computational Fluid Dynamics of Slurry Flow in Coiled Tubing to Field Data[R]. SPE 107105, 2007.

[6]鄢标, 夏成宇, 陈敏, 等. 连续管压裂冲蚀磨损性能研究[J]. 石油机械, 2016, 44(4):71-74.

YAN Biao, XIA Chengyu, CHEN Min, et al. Erosion wear characteristic of coiled tubing in fracturing operation[J]. China Petroleum Machinery, 2016, 44(4):71-74.

[7]刘少胡, 张益维, 涂忆柳. 连续管外壁冲蚀磨损规律[J]. 中国粉体技术, 2016,22(6):80-83.

LIU Shaohu, ZHANG Yiwei, TU Yiliu. Erosion wear law of coiled tubing outer wall[J]. China Powder Science and Technology, 2016, 22(6):80-83.

[8]郑华林, 张益维, 刘少胡. 水力压裂冲蚀磨损对连续管剩余寿命影响研究[J]. 中国安全生产科学技术, 2016,12(7):5-10.

ZHENG Hualin, ZHANG Yiwei, LIU Shaohu. Study on effect of erosion wear to residual life of coiled tubing for hydraulic fracturing[J]. Journal of Safety Science and Technology, 2016,12(7):5-10.

[9]王洪光. 实用焊接工艺手册[M]. 北京: 化学工业出版社, 2010:1-21.

[10]张忠厚, 李发跃. 椭圆形焊缝全自动埋弧焊装置的设计[J]. 焊接技术, 1990(4):32-34.

ZHANG Zhonghou, LI Fayue. Design of automatic submerged arc welding device for elliptical weld seam[J]. Welding Technogy, 1990(4):32-34.

[11]J. Boles, R, Burgos, A. Medina. A Field Study of Coiled-Tubing Material Loss and Ovality[R]. SPE 113669, 2008.

[12]祝效华, 刘少胡, 童华. 气体钻井钻杆冲蚀规律研究[J]. 石油学报, 2010, 31(6):1013-1017.

ZHU Xiaohua, LIU Shaohu, TONG Hua. A study on the drill pipe erosion law in gas drilling[J]. Acta Petrolei Sinica, 2010, 31(6):1013-1017.

[13]梁光川, 聂畅, 刘奇, 等. 输气管道中节流阀冲蚀数值模拟[J]. 油气田地面工程, 2013, 32(9):39-40.

LIANG Guangchuan, NIE Chang, LIU Qi, et al. Numerical simulation of throttle erosion in gas pipeline[J]. Oil-Gasfield Surface Engineering, 2013, 32(9):39-40.

[14]王龙庭. 钻井连续管力学特性研究[D]. 青岛:中国石油大学(华东), 2008:67-73.

[15]陈耀华, 覃成锦. 连续管在水平井中的力学行为研究[J]. 西部探矿工程, 2010(7):50-53.

CHEN Yaohua, TAN Chengjin. Research of the mechanical tube in horizontal wells[J]. West-china Exploration Engineering, 2010(7):50-53.

[16]杨高, 罗刚. 连续管缠绕力学研究[J]. 石油矿场机械, 2010, 39(5):10-13.

YANG Gao, LUO Gang. Mechanics research of bending coiled tubing[J]. Oil Field Equipment, 2010, 39(5):10-13.

[17]S. N. Shah, Y. Zhou, Naval Goel. Flow Behavior of Fracturing Slurries in CT [R]. SPE 74811, 2002.