基于情感神经网络的风电功率预测

2017-04-13

电信科学 2017年3期

（玉林师范学院教育技术中心，广西玉林 537000）

基于情感神经网络的风电功率预测

张国玲

（玉林师范学院教育技术中心，广西玉林 537000）

风力发电功率预测对于风能并网具有重要意义。采用一种可用于复杂系统和模式建模的新型神经网络——情感神经网络，对风力发电功率进行预测。为防止ENN在训练时陷入局部最优解，提出采用遗传算法对其进行训练。采用预测误差的均方根和标准差衡量预测准确性、稳定性，对ENN性能进行了检验。结果表明，相比于人工神经网络、支持向量机和自滑动回归模型，ENN能够获得更高的预测准确率和预测可靠性。

情感神经网络；风力发电功率；预测；遗传算法

1 引言

能源问题是当今世界难题，发展风力发电是解决能源问题的有效途径之一。但由于风的不可控性，风电场风电功率也会随机波动。这种波动随着风电的快速发展对电网影响日益增大，导致风电入网后，很难维持电力系统电源和负荷之间的平衡。针对此类问题，亟需研究者对风电功率做出预测，从而保证风电场有功控制模块系统的可靠性、安全性和可控性，帮助电力系统合理调配资源。

针对风力发电功率预测问题，目前已有大量学者对其展开研究，并先后出现基于物理和基于数学统计的预测方法[1,2]。基于物理的预测方法从天气预报数据中计算出风速、风向、气压、气温等指标数值，并综合考虑风电场周围等高线、粗糙度、障碍物、温度分层等信息计算风电机组轮毂高度的风速、风向等数值，然后依据功率曲线得出输出功率。该预测方法虽然具有物理可解释的优点，但受气象服务条件的影响。基于统计的预测方法[3]完全依赖历史统计数据，通过寻找天气状况与风电场功率之间的关系，然后依据实测数据和数值天气预报数据对风力发电功率进行预测，属于时间序列分析的范畴，典型的算法包括：自回归滑动平均[4]、Kalman滤波[5]、人工神经网络（artificial neural network，ANN）[6-8]方法和支持向量机（support vector machine，SVM）[9-11]等方法。然而，风的大小和风向是多种因素综合的结果，具有很强的波动性和不确定性，导致风电功率的时间序列也往往具有很强的动态性和非线性。因此需要一种能够描述更加复杂的非线性系统的模型进行预测。

情感神经网络（emotionalneuralnetwork，ENN）[12]是一种仿照人类情感处理组织设计出的新型神经网络结构，具有反应速度快、非线性能力强等特点，可以成功描述地球磁场[13,14]这一复杂系统。但目前将其应用于风电功率预测研究甚少，因此本文采用ENN对风电功率进行预测。

2 情感神经网络

情感神经网络仿照人脑的边缘系统（limbic system）建立，其实质是一个包含了杏仁核（amygdale）、框额皮层（orbitofrontal cortex）、丘脑（thalamus）、感觉皮层（sensory cortex）的4层神经网络。典型的情感神经网络结构如图1所示。

图 1中的 pj,j=1,…,n+1表示输入特征，vj,j=1,…,n+1和 wj,j=1,…,n+1表示权重，c表示偏移，E、Ea和 Eb表示输出，其计算过程如下。

假设用向量 P=[p1,p2,p3,…,pn]表示整个系统的输入，则特征进入丘脑后，首先计算模糊特征pn+1，并将其作为杏仁核中的神经元的输入之一。模糊特征pn+1用通过求解输入特征的均值得到。

另外，原始输入P经丘脑后还会直接进入感觉皮层，感觉皮层的输入汇同模糊特征作为输入进入杏仁核，杏仁核的输出Ea可以表示为：

其中，f(·)表示激励函数。感觉皮层的输出还会传输到框额皮层，框额皮层的输出Eb可以表示为：

框额皮层用于抑制模糊的判断，则系统最终的输出E是两部分输出之差：

3 基于遗传算法的ENN训练

图1 典型的情感神经网络架构

反向传播（back propagation，BP）算法是最常用的神经网络训练方法，参考文献[15,16]表明采用 BP算法同样可以对ENN进行训练。然而，BP算法从单个初始值迭代求最优解，求解结果依赖于初始权值的选择，因此该算法存在收敛速度缓慢而且容易陷入局部最优解的缺点。遗传算法（genetic algorithm，GA）从串集开始搜索，覆盖面大，利于全局择优。为此本文采用遗传算法对ENN进行训练。

3.1 染色体和适应度函数

当给定一组样本[Pk,Tk]时，对ENN进行训练的实质是，通过调整权重和偏移，使得由ENN计算得到的输出Yk与样本的目标输出Tk之间的误差最小。

遗传算法寻求能够最小化适应度函数的染色体，得到最优解。每个染色体都是对潜在解的编码，而适应度函数则是优化目标。采用遗传算法对ENN进行训练时，采用浮点编码法进行编码，构造出的染色体形式如式（5）所示。

因此当输入特征长度为n时，染色体长度为2n+2，假设给定输入特征Pk，则ENN的输出Yk可以根据式（1）～式（4）计算得到，并且记：

其中，choromn表示当前的染色体，从当前的染色体当中可以解码出 ENN当前的各个权重和偏移值，Ψ(·)表示综合式（1）～式（4）的计算过程。染色体的适应度函数为：

其中，Tk为给定输入特征Pk时对应的目标输出，因此最小化适应度函数就意味着最小化ENN输出与目标输出之间的误差。

3.2 基于GA的训练算法

针对式（7）中适应度函数，遗传算法通过借鉴生物界的进化规律（适者生存、优胜劣汰遗传机制），采用交叉、变异等操作完成使式（7）最小化的随机化搜索，整个训练算法流程给定如下,其中采用轮盘赌算法对染色体种群进行了初始化，图2中的适应度根据式（7）得到。

图2 基于GA的ENN训练算法流程

4 实验结果与性能分析

采用我国东北某风力发电厂的风电功率数据对本文所提方法进行了验证。该数据集以小时为单位对风电发电功率进行了记录，共包含了8 945 h的数据，如图3所示。将这8 945 h的功率数据分为两部分，一部分用于训练神经网络（前 4 000 h数据），另一部分用于测试神经网络（后4 945 h数据）。数据在使用前被归一化到[0,1]区间当中，采用参考文献[17]中的方法确定出采用前18 h的数据去预测第19 h的数据。所提的ENN和基于GA的学习算法均通过MATLAB R2012a进行仿真。采用均方根误差和误差的标准差作为衡量指标，并通过与人工神经网络、支持向量机和自回归滑动平均算法（auto-regressive and moving average model，ARMA）对比给出结果。

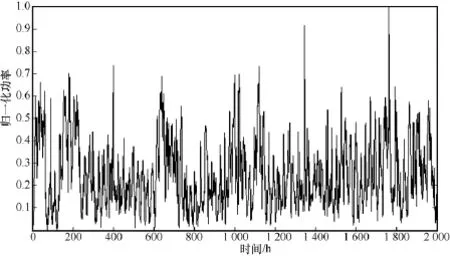
图3 东北某风力发电厂的风电功率

采用人工神经网络算法进行预测时，训练算法选用BP算法，考虑了隐含层层数为5、10、15、20和25的5种情况，并以均方误差和误差的标准差作为衡量指标给出预测，结果见表1。

表1 采用BP人工神经网络的预测结果

从表1中可以看出，隐含层个数为5个时，人工神经网络取得最好的分类效果，因此最终确定人工神经网络结构为18-5-1。

采用支持向量机进行预测时，采用参考文献[11]的方法进行，采用AMRA算法进行预测时，采用参考文献[4]中的方法进行。最终，4种方法的预测结果对比如图4所示。

图4 BP-ANN、GA-ENN、SVM、AMRA 4种方法的风电功率预测结果对比

图4（a）给出了测试数据中52 h的预测结果，图4（b）给出了4种方法预测结果的统计结果。从图4(a)中可以看出，相比于ANN、SVM和AMRA，ENN的预测结果与真实数据的趋势更加相近。从图4(b)可以看出，在ANN、SVM和AMRA3种算法中，采用结构为18-5-1的ANN进行预测时可以获得最高的预测准确性；采用 SVM进行预测时，在进行的23次试验中偏差的标准差为0.005 9，在3种算法中最低，说明SVM算法的预测结果较ANN和AMRA的稳定性更好。而采用ENN对给定数据集进行预测时，预测的均方根误差从0.596 7降低到了0.573 6，准确率提高了3.87%。对得到的误差标准差的进行对比发现，人工神经网络取得0.059的标准差，而ENN的误差标准差仅为0.034，降低42.3%，表明采用ENN对风电功率数据进行预测时，预测偏差波动更小、可靠性更高。综合两个指标可以得出，相比于ANN、SVM和AMRA，采用ENN在对风电功率进行预测时能够预测的准确率和可靠性，具有优势。

5 结束语

由于风的不可控性，导致风力发电功率预测成为一个难题。为揭示风电功率历史数据中存在的复杂的模式，本文采用情感神经网络对风电功率进行了预测。针对BP算法容易陷入局部最小值的缺陷，采用遗传算法ENN进行了训练。以东北某风力发电厂的风力发电数据为例，对本文所提方法进行了验证，结果表明：相比于ANN、SVM和AMRA，ENN能够提高预测准确率和预测可靠性。由于ENN具有更加复杂的结构，因此也具有更强的非线性能力，这可能是导致ENN在对风电功率预测时取得更好的预测效果的原因。但ENN在其他复杂问题当中的应用效果还有待于进一步研究。

[1] 谷兴凯,范高锋,王晓蓉,等.风电功率预测技术综述 [J].电网技术,2007(S2):335-338. GU X K,FAN G F,WANG X R,et al.Summarization of wind power prediction technology [J].Power System Technology, 2007(S2):335-338

[2] 王健,严干贵,宋薇,等.风电功率预测技术综述 [J].东北电力大学学报,2011,31(3):20-24. WANG J,YAN G G,SONG W,et al.Summarization of wind power prediction technology[J].Journal of Northeast Dianli University,2011,31(3):20-24.

[3] 范高锋,裴哲义,辛耀中.风电功率预测的发展现状与展望[J].中国电力,2011,44(6):38-41. FAN G F,PEI Z Y,XIN Y Z.Wind power predictionachievement and prospect[J].Electric Power,2011,44(6): 38-41.

[4]冬雷,王丽婕,郝颖,等.基于自回归滑动平均模型的风力发电容量预测[J].太阳能学报,2011,32(5):617-622. DONG L,WANG L J,HAO Y,et al.Prediction of wind power generation based on auto regressive moving average model[J]. Acta Energiae Solaris Sinica,2011,32(5):617-622.

[5]修春波,任晓,李艳晴,等.基于卡尔曼滤波的风速序列短期预测方法[J].电工技术学报,2014(2):253-259. XIU C B,REN X,LI Y Q,et al.Short-term prediction method of wind speed series based on Kalman filtering fusion [J]. Transactions of China Electrotechnical Society,2014(2):253-259.

[6]CATALAO J P S,POUSINHO H M I,MENDES V M F.An artificial neural network approach for short-term wind power forecasting in portugal[J].International Journal of Engineering Intelligent Systems for Electrical Engineering&Communications, 2009,17(1):1-5.

[7]HANADA K,HAMAJIMA T,TSUDA M,et al.Wind power forecasting using an artificial neural network for ASPCS[J]. Energy&Power Engineering,2013,5(4):414-417.

[8] 范高锋,王伟胜,刘纯,等.基于人工神经网络的风电功率预测[J].中国电机工程学报,2008(34):118-123. FAN G F,WANG W S,LIU C,et al.Wind power prediction based on artificial neural network[J].Proceedings of the CSEE, 2008(34):118-123.

[9]ZENG J,QIAO W.Support vector machine-based short-term wind power forecasting [C]//Power Systems Conference and Exposition March 20-23,2011,Phoenix,AZ,USA.New Jersey: IEEE Press,2011:1-8.

[10]MATHABA T,XIA X,ZHANG J.Short-term wind power prediction using least-square support vector machines[C]//Power Engineering Society Conference and Exposition in Africa,March 20-23,2011,Phoenix,AZ,USA.New Jersty:IEEE Press,2012:1-6.

[11]丁志勇,杨苹,杨曦,等.基于连续时间段聚类的支持向量机风电功率预测方法[J].电力系统自动化,2012,36(14):131-135. DING Z Y,YANG P,YANG X,et al.W ind power prediction method based on sequential time clustering support vector machine[J].Automation of Electric Power Systems,2012,36(14): 131-135.

[12]LOTFI E,AKBARZADEH T M R.Practical emotional neural networks[J].Neural Networks,2014,59(11):61-72.

[13]PAVLOS G P,ILIOPOULOS A C,TSOUTSOURAS V G,et al. First and second order non-equilibrium phase transition and evidence for non-extensive Tsallis statistics in earth’s magnetosphere [J].Physica A Statistical Mechanics& its Applications,2011,390(15):2819-2839.

[14]BABAIE T,KARIMIZANDI R,LUCAS C.Learning based brain emotional intelligence as a new aspect for development of an alarm system [J].Soft Computing-A Fusion of Foundations, Methodologies and Applications,2008,12(9):857-873.

[15]KHASHMAN A.Modeling cognitive and emotional processes:a novel neural network architecture [J].Neural Networks the Official Journal of the International Neural Network Society, 2010,23(10):1155-1163.

[16]KHASHMAN A.A modified backpropagation learning algorithm with added emotional coefficients [J].IEEE Transactions on Neural Networks,2008,19(11):1896-1909.

[17]QUAN H,SRINIVASAN D,KHOSRAVI A.Short-term load and wind power forecasting using neural network-based prediction intervals[J].IEEE Transactions on Neural Networks&Learning Systems,2014,25(2):303-315.

An emotional neural network based approach for wind power prediction

ZHANG Guoling
Center of Education Technology,Yulin Normal University,Yulin 537000,China

Accurate wind power forecasting is vital for the integration of wind power into the grid.Emotional neural network (ENN)——a new type of neural network which could be used to model complex systems and patterns,was used to forecast wind power.To prevent ENN from stucking in locally optimal solution in the process of training, genetic algorithm was proposed to train ENN.The root-mean-square and the standard deviation of the forecast errors were also adopted to measure the accuracy and reliability of the forecast to test the performance of ENN.The results demonstrate that,compared with artificial neural network,ENN can improve the accuracy and reliability of the forecast by 3.8%and 46%respectively.

emotional neural network,wind power,prediction,genetic algorithm

TP183

：A

10.11959/j.issn.1000-0801.2017005