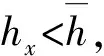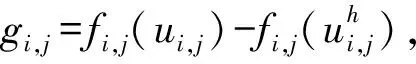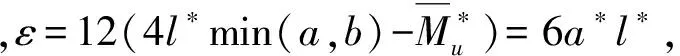一类偏微分方程边值问题的有限差分格式
2017-04-13武文佳
武文佳
(上海电机学院 数理教学部, 上海 201306)
一类偏微分方程边值问题的有限差分格式
武文佳
(上海电机学院 数理教学部, 上海 201306)
对一类二维常系数椭圆型偏微分方程,建立了一种四阶紧有限差分格式。证明了有限差分解的存在性和唯一性,用离散能量分析的方法给出了数值解的L2-范数和H1-范数误差估计。
常系数椭圆边值问题; 紧有限差分格式; 误差估计
偏微分方程在自然科学、工程技术、力学、生物学以及化学等领域都有着广泛的应用。科学和工程中的许多数学模型都可以用偏微分方程来描述[1-3],对偏微分方程的求解在科学研究过程中尤为重要。绝大多数偏微分方程的定解问题都无法给出精确的解析解,因此,微分方程的数值求解引起了学者广泛的关注。
近年来,有限元方法、有限差分及谱方法等已经成为微分方程数值求解的主要方法[4-9]。有限差分方法是用于求解微分方程定解问题最常用的数值逼近方法。本文对一类常系数二维椭圆型偏微分方程,建立了一种四阶紧有限差分方法,并给出了相应的理论分析。
1 四阶有限差分格式的建立
本文主要研究如下二维常系数椭圆边值问题:
(1)
式中,Ω⊂R2为矩形区域的组合;函数f(x,y,u)和φ(x,y)在定义域内充分光滑,函数f(x,y,u)关于u为非线性的;a、b、c、d为不依赖于(x,y)的常数,且a>0,b>0。
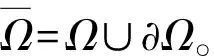
(2)
引入如下中心差分算子:
(3)
用上述算子替换式(1)中的微分算子,得
(4)
式中,τi,j为截断误差,
(5)
(6)
式中,系数
(7)
定义有限差分算子
(8)
设σ=hx/hy为步长比,计算可得
(9)
式中,
(10)
且
(11)
(12)
显然,由式(11)可知,存在正常数h*,使得对所有的hx q(k1,k2)≥0,k1,k2=-1,0,1 (13) 上述性质表明算子Ph为非负的。假设 (14) 同样由式(10)、(11)可知,给定任意非负常数M,存在正常数h(M),使得对所有的hx (15) 在实际计算中,h(M)和h*的精确值可通过计算p(k1,k2)和q(k1,k2)得到[11]。 (16) 定理1表明,算子Lh具有连续算子同样的极值原理。 本文用上、下解的方法研究紧有限差分格式(式(12))解的存在性和唯一性。首先给出差分格式(式(12))的上、下解的定义。 (17) 且引入如下记号: (18) (i,j)∈Ωh 引理1 假设式(14)成立,M为非负常数。若hx (19) 证明 根据式(19),结合文献[13]中260页的定理1可证引理1的结论成立。 由引理1可得到极大解和极小解的存在性结果如定理2所示。 定理 2 假设式(14)成立,如果 证明 取迭代初始值 通过Picard型迭代 (20) (21) (22) 再根据引理1可得 即 同理可证 这就证明了式(21)在m=1时的情形。最后,由数学归纳法可知,对所有的m≥1,式(21)均成立。 由式(21)可知,极限 改革开放初期,上海主要电源点仅有闸北、杨树浦、南市、闵行和吴泾电厂,电力供应特别紧张。经过40年的发展,上海电力供应形成1/3市内和2/3市外的总格局,基本解决了电力供应保障的问题。 (23) 存在且满足 (24) (25) 记 ∂xvi,j=(vi+1,j-vi,j)/hx ∂yvi,j=(vi,j+1-vi,j)/hy 对任意的vi,j∈Vh,引入如下Sobolev范数: (26) 简单计算可知,对任意vi,j,ωi,j∈Vh,有 (27) 及 (28) 引理2 对任意vi,j∈Vh,有以下估计式: (29) 证明 (2) 为了证明式(29)中第2个估计式,注意到 (30) 式中, (31) 则由式(27)、(28),有 (32) 且 (33) 由式(27)可知 (δxv,v)=-(v,δxv) 这说明 同理可得 因此有 (L3v,v)=0 (34) 将式(32)~(34)代入式(30),可得到式(29)中第2个估计式。 (3) 根据式(27)可得 这就证明了式(29)的第3个估计式成立。 下面根据上述引理2,证明有限差分解的唯一性。 定理3 设定理2的条件成立,若 (35) (36) (37) 这表明 因此由引理2可得 再结合式(35)可知 即对所有的(i,j)∈Ωh,有 定理3表明,本文构造的紧有限差分格式(式(12))的解是唯一的。 (38) (39) (40) 式中, (41) 则当hx 故可得 由上述估计和引理2可知式(41)成立。 定理4表明,本文建立的紧有限差分格式具有四阶精度。 [1] LIAO Wenyuan. A fourth-order finite-difference method for solving the system of two-dimensional Burgers’equations [J]. International Journal for Numerical Methods Fluids, 2010,64(5): 565-590. [2] ÖZISIK M N. Boundary Value Problems of Heat Conduction [M]. New York:Dover Publications,1989. [3] GUPTA M M,MANOHAR R P,STEPHENSON J W. High-order difference schemes for two-dimensional elliptic equations [J]. Numerical Methods for Partial Differential Equations,1985(1):71-80. [4] BERIKELASHVILI G, GUPTA M M,MIRIANA-SHVILI M. Convergence of fourth order compact difference schemes for three-dimensional convection-diffusion equations [J]. SIAM Journal on Numerical Analysis,2007,45(1):443-455. [5] GOPAUL A,BHURUTH M. Analysis of a fourth-order scheme for a three-dimensional convection-diff-usion model problem [J]. SIAM Journal on Scientific Computing,2006,28(6):2075-2094. [6] WANG Xuan,YANG Zhifeng,HUANG G,et al. A high-order compact difference scheme for 2D Laplace and Poisson equations in non-uniform grid systems [J]. Communications in Nonlinear Science and Numerical Simulation,2009,14(2):379-398. [7] WANG Jie,ZHONG Weijun,ZHANG Jun. A general meshsize fourth-order compact difference discretization scheme for 3D Poisson equation [J]. Applied Mathematics and Computation,2006,183(2):804-812. [8] ZHANG Jun. Multigrid method and fourth-order compact scheme for 2D Poisson equation with unequal mesh-size discretization [J]. Journal of Computational Physics,2002,179(1):170-179. [9] 张蕾.几类偏微分方程非标准有限差分格式的研究 [D].哈尔滨,哈尔滨工业大学,2014:1-12. [10] SUTMANN G,STEFFEN B. High-order compact solvers for the three-dimensional Poisson equation [J]. Journal of Computation and Applied Mathematics,2006,187(2):142-170. [11] 武文佳.一类二维半线性椭圆边值问题的四阶紧有限差分格式 [J].上海电机学院学报,2013,16(1/2):88-92. [12] 武文佳. 一类椭圆边值问题紧有限差分方法的单调迭代算法 [J].上海电机学院学报,2014,17(5):283-287,310. [13] SAMARSKII A A. The Theory of Difference Schemes [M]. New York:Marcel Dekker, Inc, 2001:260. [14] SUN Z Z. Numerical Methods of Partial Differential Equations [M]. Beijing: Science Press,2005:260. Finite Difference Scheme for a Class of Boundary Value Problems WUWenjia (Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306,China) A fourth-order compact finite difference scheme is proposed for a class of two-dimensional elliptic boundary value problems with the constant coefficients. Existence and uniqueness of finite difference solutions are investigated. Convergence and the fourth-order accuracy of the proposed method are shown with respect to discreteL2-andH1-norm. elliptic boundary value problem with constant coefficients; compact finite difference scheme; error estimation 2016 -11 -13 上海电机学院学科建设项目资助(16JCXK02) 武文佳(1985-),女,讲师,博士,主要研究方向为偏微分方程数值解,E-mail: wuwj@sdju.edu.cn 2095 - 0020(2017)01 -0056 - 07 O 241.82 A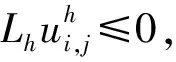
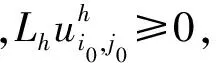
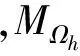
2 有限差分解的存在性
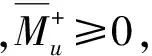
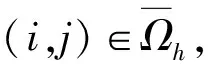
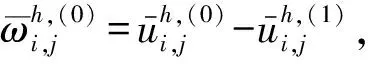
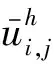
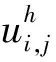
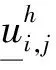
3 有限差分解的唯一性
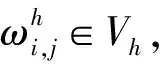
4 有限差分格式的误差分析