B型非交错连接分拆的两个计数结果
2017-04-13崔汉哲
崔汉哲
(上海电机学院 数理教学部,上海 201306)
B型非交错连接分拆的两个计数结果
崔汉哲
(上海电机学院 数理教学部,上海 201306)
连接分拆与非交错连接分拆是组合数学中的一类重要研究对象。对于[±n]的所有B型非交错连接分拆组成的集合NCL(B)(n),分别计算其中包含或不包含零分块的元素个数。找到其满足的递推关系,并得出生成函数的表达式。
B型非交错连接分拆; 零分块; 递推式; 生成函数
组合数学中,连接分拆(linked partitions)与非交错连接分拆(noncrossing linked partitions)作为一类重要的内容被研究。它们最早由Dykema[1]在经典非交换概率论的T—变换研究时引入,之后被广泛应用于非交换概率论的其他方面以及算子代数的研究中[2-7]。同时,不同学者从多角度研究了连接分拆与非交错连接分拆作为组合对象的丰富性质,如代数结构[8]、计数性质、与其他组合对象的联系[10-13]等。
另一方面,文献[14]中从与组合数学有密切联系的Coxeter群的分类角度出发,定义了A、B和D型组合对象。在此基础上,文献[15]中定义了B型非交错连接分拆,研究了它们的基本性质,并与文献[16]共同得到了一些基本的计数结果。具体而言,文献[15]中计算了集合[±n]={1,2,…,n,-1,-2,…,-n}的所有B型非交错连接分拆的个数。本文进一步计算集合[±n]的B型非交错连接分拆中包含或不包含零分块的元素个数。
1 定义与引理
在集合{1,2,…,n,-1,-2,…,-n}上定义全序关系1<2<… 对于a∈Z,定义绝对值映射abs∶Z→N为 对于Z的子集V,定义 若集合π以Z的若干子集为元素,则类似定义 文献[8]中的定义2、3给出了连接分拆与非交错连接分拆的定义,此处不赘。记[n]的所有连接分拆组成的集合为LP(n),[n]的所有非交错连接分拆组成的集合为NCL(n)。为叙述完整,本文先给出B型连接分拆和B型非交错连接分拆的定义。 定义1[15][±n]的一个B型连接分拆(linked partition of type B)是指以[±n]的若干子集为元素的集合π,且满足以下条件: (1) absπ∈LP(n); (2) 由V∈π可得-V∈π; (3)π中至多有一个元素W满足W=-W。此时,称W为π的零分块。 注意:由条件(1)和(2)可知,π中所有元素之并为[±n]。记[±n]的所有B型连接分拆组成的集合为LP(B)(n)。对于π∈LP(B)(n),称π的元素为块或分块。若i,j∈[±n]属于π中的同一分块,则记i~πj(当上、下文意义明确时,可省略下标)。若π中分块彼此非交错,即不存在如下情况:a,b,c,d∈[±n],a、c属于π的某一分块,b、d属于π的另一分块,且在[±n]的全序关系之下有a π|S={V∩S|V∈π,V∩S≠∅} 称其为将π限制到S后所得的连接分拆。最后,将NCL(B)(n)中所有包含零分块的元素组成的集合记为NCLZ(B)(n)。本文目的为计算|NCLZ(B)(n)|和|NCL(B)(n)NCLZ(B)(n)|。 以下B型连接分拆与非交错连接分拆的几个简单性质见文献[15],在本文的证明中将要用到。 性质1 若π∈LP(B)(n),p∈[±n],则p在π中为单覆盖或双重覆盖。且 (1)p在π中为单覆盖⟺-p在π中为单覆盖⟺absp在absπ中为单覆盖; (2)p在π中为双重覆盖⟺-p在π中为双重覆盖⟺absp在absπ中为双重覆盖。 性质2 ±1,±n在π∈LP(B)(n)中均为单覆盖。 性质3 若π∈NCL(B)(n),则absπ∈NCL(n)。 下文的2个引理总结了文献[9]、[15]中关于NCL(n)与NCL(B)(n)的一些计数结果。 则S(x)满足方程 S2(x)+(x-1)S(x)+x=0 (1) 即 (2) sn满足的递推关系为s1=1;当n≥2时, sn=sn-1+s1sn-1+s2sn-2+…+sn-1s1 (3) 注:本文中的生成函数与文献[9]中稍有不同,略去了常数项1。因此,式(1)以及方程的解是改写后的结果。下同。 引理2 设n∈N,记 则 (4) 式中,fn满足的递推关系为f1=2,f2=6;当n≥3时, (5) 定理1 设n∈N,记 则 (6) 式中,hn满足的递推关系:h1=1,h2=3;当n≥3时, (7) 证明 由NCLZ(B)(1)={{{1,-1}}}可知h1=1。 由NCLZ(B)(2)={{{1,-1},{2},{-2}},{{1},{-1}{2,-2}},{{1,2,-1,-2}}}可知h2=3。 设π∈NCLZ(B)(n)且n≥3。将元素-n所在分块记为V,将在[±n]的全序之下的V中最小元记为v。分以下6种情况讨论。 (1)v=-n。此时,V={n}且{n}与{-n}同时为单点块。由性质2可知,n与-n在π中均为单覆盖。于是,π|[±(n-1)]∈NCLZ(B)(n-1),且π|[±(n-1)]可以是NCLZ(B)(n-1)中的任意元素,故π的个数为hn-1。 (2)v=n。此时V={n,-n}恰为π中的零分块。由非交错条件可知,π|[n-1]∈NCL(n-1),且π|[n-1]可以是NCL(n-1)中的任意元素,π的个数为sn-1。 (3)v=-1。此时,n∈-V且V(-V)不为零分块。由非交错条件可知,此时π中没有零分块,即π∉NCLZ(B)(n)。由题设,此情况可略去不计。 (4)v=1。此时,π|[±(n-1)]∈NCLZ(B)(n-1),且π|[±(n-1)]可以是NCLZ(B)(n-1)中的任意元素,故π的个数为hn-1。 (5)v∈{2,3,…,n-1}。此时,由非交错条件可知,π|{1,2,…,v}为NCL(v)中任意元素,而π|{v,v+1,…,n,-v,-v-1,…,-n}为{v,v+1,…,n,-v,-v-1,…,-n}上的一个包含零分块的B型非交错连接分拆,且满足v~-n(-v~n),于是进一步有 π|{v,v+1,…,n -1,- v,- v -1,…,-(n-1)}∈NCLZ(B)(n-v) 且可以是NCLZ(B)(n-v)中的任意元素。 反之,对于{1,2,…,v}的一个非交错连接分拆π1,以及{v,v+1,…,n,-v,-v-1,…,-n}上的一个包含零分块的B型非交错连接分拆π2满足v~π2(-n)(-v~π2n),可以相应得到 π∈NCLZ(B)(n) 且-n所在分块在[±n]的全序之下的最小元为v。具体构造如下: (8) 由此可知,π的个数为s2hn-2+s3hn-3+…+sn-1h1。 (6)v∈{-2,-3,…,1-n}。此时,-v,n∈-V且V(-V)不为零分块。由非交错条件可知, π|{1,2,…,-v,-1,-2,…,v}∈NCLZ(B)(-v) {σ∈NCLZ(B)(-v)|v~σ(-v)} 且可以是该集合中的任意元素。而π|{v,v-1,…,-n}为{v,v-1,…,-n}的非交错连接分拆且满足v~-n,因此,π|{v,v-1,…,-n∈NCL(n+v)。 反之,给定 NCLZ(B)(-v){σ∈NCLZ(B)(-v)|v~σ(-v)} 中元素与集合{v,…,-n}上满足v~-n的非交错连接分拆,类似情况(5)中的构造,可以得到满足情况(6)条件的[±n]上包含零分块的B型非交错分拆。而由对称性、非交错条件以及映射abs,类似情况(2)中的讨论,可知集合 {σ∈NCLZ(B)(-v)|v~σ(-v)}= {σ∈NCL(B)(-v)|v~σ(-v)}≅NCL(-v) 由此可得情况(6)中π的个数为 sn-2(h2-s2)+sn-3(h3-s3)+…+s1(hn-1-sn-1) 综合上述6种情况,可知n≥3时,fn的递推式如下: hn=2hn-1+sn-1+(s2hn-2+s3hn-3+…+sn-1h1)+sn-2(h2-s2)+sn-3(h3-s3)+ …+s1(hn-1-sn-1) (9) 结合s1=1与s2=3,将式(9)改写为 hn=hn-1+sn-1+2(s1hn-1+s2hn-2+…+sn-1h1)-(s1sn-1+s2sn-2+…+sn-1s1) (10) 再由生成函数的定义可将式(10)改写为 (11) 最后,将引理1中S(x)的已知结果代入式(11),整理后即得 (12) 证毕。 由定理1以及引理2可直接计算NCL(B)(n)中不包含零分块的元素个数。 推论1 设n∈N,记 则 (13) 式中,gn满足的递推关系为g1=1,g2=3;当n≥3时, (14) 注记 用定理1证明中推导H(x)的方法也可以直接得到推论1的结果。g1=1、g2=3易得,然后类似定理1的证明,分6种情况讨论。下文只写出每种情况对应的元素个数K,具体过程略去。 (1)K=gn-1; (2)K=0; (3)K=sn-1; (4)K=gn-1; (5)K=s2gn-2+s3gn-3+…+sn-1g1; (6)K=g2sn-2+g3sn-3+…+gn-1s1。 由此,同样可得gn满足的递推关系以及G(x)的表达式。 [1] DYKEMA K J. Multilinear function series and transforms in free probability theory [J].Advances in Mathematics, 2007, 208(1): 351-407. [2] POPA M. Non-crossing linked partitions and multiplication of free random variables [J].arXiv, 2008:0812.2064, . [3] NICA A. Non-crossing linked partitions, the partial order onNC(n), and the S-transform [J].Proceedings of the American Mathematical Society, 2010, 138(4): 1273-1285. [4] POPA M, WANG J C. On multiplicative conditionally free convolution [J].Transactions of the American Mathematical Society, 2011, 363(12): 6309-6335. [5] ARIZMENDI O, VARGAS C. Product of free random variables and k-divisible non-crossing partitions[J].Electronic Communication in Probability, 2012, 17(5):489-500. [6] POPA M. A Fock space model for addition and multiplication of c-free random variables [J].Proceed-ings of the American Mathematical Society, 2014, 142(6): 2001-2012. [7] POPA M, VINNIKOV V, WANG J C. On the multiplication of operator-valued c-free random variables [J].arXiv,2015:1509.08853. [8] 崔汉哲. 非交错连接分拆的等价描述 [J].上海电机学院学报,2012,15(6):409-413. [9] CHEN W Y C, WU S Y J, YAN C H. Linked partitions and linked cycles [J].European Journal of Combinatorics, 2008, 29(6): 1408-1426. [10] CHEN W Y C, WANG C J. Noncrossing linked partitions and large (3, 2)-Motzkin paths [J].Dis-crete Mathematics, 2012, 312(11): 1918-1922. [11] CHEN W Y C, LIU L H, WANG C J. Linked partitions and permutation tableaux[J].arXiv, 2013,1305.5357 [12] CHEN W Y C, GUO P L, PANG S X M. Vacillat-ing Hecke tableaux and linked partitions [J]. Mathematische Zeitschrift, 2015, 281(3): 661-672. [13] YAN S H F, ZHOU R. Refined enumeration of corners in tree-like tableaux[J]. arXiv,2017:1701.07216. [14] REINER V. Non-crossing partitions for classical reflection groups[J]. Discrete Mathematics, 1997, 177(1/3): 195-222. [15] 崔汉哲. B型非交错连接分拆及其计数 [J]. 上海电机学院学报,2015,18(1):42-45. [16] 崔汉哲. B型非交错连接分拆的一个计数结果 [J]. 上海电机学院学报,2016,19(2):121-124. [17] STANLEY R P. Enumerative combinatorics[J]. Cambridge Studies in Advanced Mathematics. 1999,62(2):178,291. [18] SLOANE N J. The on-line encyclopedia of integer sequences (OEIS) [EB/OL]. [2016-08-26].http://oeis.org/search?q=A006138&language=english &go=Search. Two Enumerative Results for Noncrossing Linked Partitions of Type B CUIHanzhe (Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China) Linked partitions and non-crossing linked partitions are both important combinatoric objects. We calculate the cardinal numbers of the sets that consist of non-crossing linked partitions of type B on [±n] with or without zero blocks. Their recurrence formulas and generating functions are obtained. noncrossing linked partitions of type B; zero block; recurrence formula; generating functions 2016 -12 -25 崔汉哲(1980-), 男,讲师,博士,主要研究方向为泛函分析和组合数学,E-mail:cuihz@sdju.edu.cn 2095 - 0020(2017)01 -0052 - 04 O 157.1 A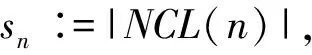
2 定理、推论及其证明
