基于自适应LMS的电路谐波电流检测

徐鹏辉, 胥 飞

(上海电机学院 电气学院，上海 201306)

基于自适应LMS的电路谐波电流检测

徐鹏辉, 胥 飞

(上海电机学院 电气学院，上海 201306)

为滤除电路中的谐波，需要精确地检测出电路中所含的谐波量。研究了自适应最小均方误差(LMS)谐波电流检测算法。用自适应滤波器取代低通滤波器，解决了谐波检测实时性问题。自适应LMS谐波电流检测算法对电网电压畸变、频率波动等电网参数变化具有良好的自适应调节能力，可运用于三相或单相电路，改变算法中的收敛因子，加快了谐波的检测速度。Matlab仿真结果验证了新算法的精确性和实时性。

谐波检测； 自适应滤波器； 最小均方误差； 收敛因子

随着电力电子技术广泛应用于工业领域，电网中的谐波污染问题也越来越严重。谐波的存在会使电气设备出现过热情况，加速了设备老化，降低了使用寿命，甚至引发设备故障或烧毁；另外，谐波也可能引起继电保护和自动装置产生误动作，造成电力系统故障[1]。

为了消除电路中的谐波含量，就要对电路中的谐波量进行精确测量，需要采用一定的测量方法计算出电路中所含的谐波总量。目前，常用的谐波检测方法是瞬时无功功率检测法，由 Akagi 等[2]于1983年提出，即p-q理论，定义了瞬时有功功率p、瞬时无功功率q，该方法计算简单，但误差较大，谐波含量较高。文献[3]中提出了ip-iq理论，即定义瞬时有功电流ip、瞬时无功电流iq，间接求出p、q,该方法计算简单，但只适用于三相电路，不适合于单相电路，且无法检测出谐波中的任意次谐波。文献[4]中研究的d-q谐波和无功功率检测法，谐波检测量较高，但在三相不对称电路中，因检测电路复杂，降低了检测精度。文献[5]中研究的d-q-0谐波电流检测法运算速度快，但是对电流、电压的同步采样要求较高，无法满足实时性要求。文献[6-7]中提出的自适应谐波检测法，检测精度高，但是结构中含有的滤波器器件较多，结构复杂，计算繁琐。文献[8-9]中提出的基于神经元的自适应算法，控制和计算精度较高，但是计算过程复杂，运算速度较慢，不适用于实时变化的谐波电路。

本文提出的自适应最小均方误差(Least Mean Square, LMS)谐波电流检测法，是在自适应噪声对消技术[10]及自适应滤波器[11]基础上发展起来的电流检测算法，主要针对不确定对象，尤其是时变、非线性和随机系统,不仅可以精确检测三相电路、单相电路中的谐波量，而且可以检测非对称电路中的谐波量。该方法自适应能力强，所需模块少，计算简单，动态性高。

1 自适应LMS滤波器

自适应LMS谐波检测法是在自适应噪声对消技术的基础上，由含有1个90°移相因子的二阶陷波[12](交流输入电流从一相切换到另一相时产生的周期性电压扰动)滤波器的闭环连续系统组成。

图1 自适应LMS滤波器结构图

假设电源电压为标准的正弦信号us(t)=usin(lt)，其中，u为电压幅值，l为周期，记流过非线性负载周期性、非线性电流为iL(t)，其傅氏级数展开式[14]为

iL(t) =I1cos(ψ1)sin(lt)+I1sin(ψ1)cos(lt)+

i1p(t)+i1q(t)+ih(t)=i1p(t)+if(t),

k=2,3,…，n,n∈N

(1)

同理，以采样间隔Ts对iL(t)进行采样，则

(2)

2 自适应LMS电流谐波检测算法

本文研究的自适应LMS电流谐波检测算法，用代价函数中对权值系数的瞬时梯度来代替最速下降算法[15]中的统计梯度。

由图1知，权矢量为w1(n)和w2(n),输入向量为x1(n)和x2(n),可得

y(n)=x1(n)w1(n)+x2(n)w2(n)

(3)

式(3)满足输入量与输出量之间的线性组合关系。

设输入向量X=(x1,x2,…,xk)T，则有k个权矢量W=(w1,w2,…,wk)T，由式(3)可得

y(n)=XT(n)W(n)=WT(n)X(n)

(4)

图2给出了自适应LMS算法的结构图。其中，I为单位矩阵，Z-1I为延时一段时间的矩阵，它属于一个闭环控制系统,由两部分组成:一部分是滤波过程，由输入信号u(n)和权矢量w(n)计算出输出信号y(n)，与期望信号d(n)相比较后得到误差值e(n)；另一部分是自适应校正过程，将输出e(n)与梯度矢量自动更新的权矢量w(n)反馈到输入侧得到w(n+1),重新计算输出值，使之接近于期望信号，得到最佳权矢量。

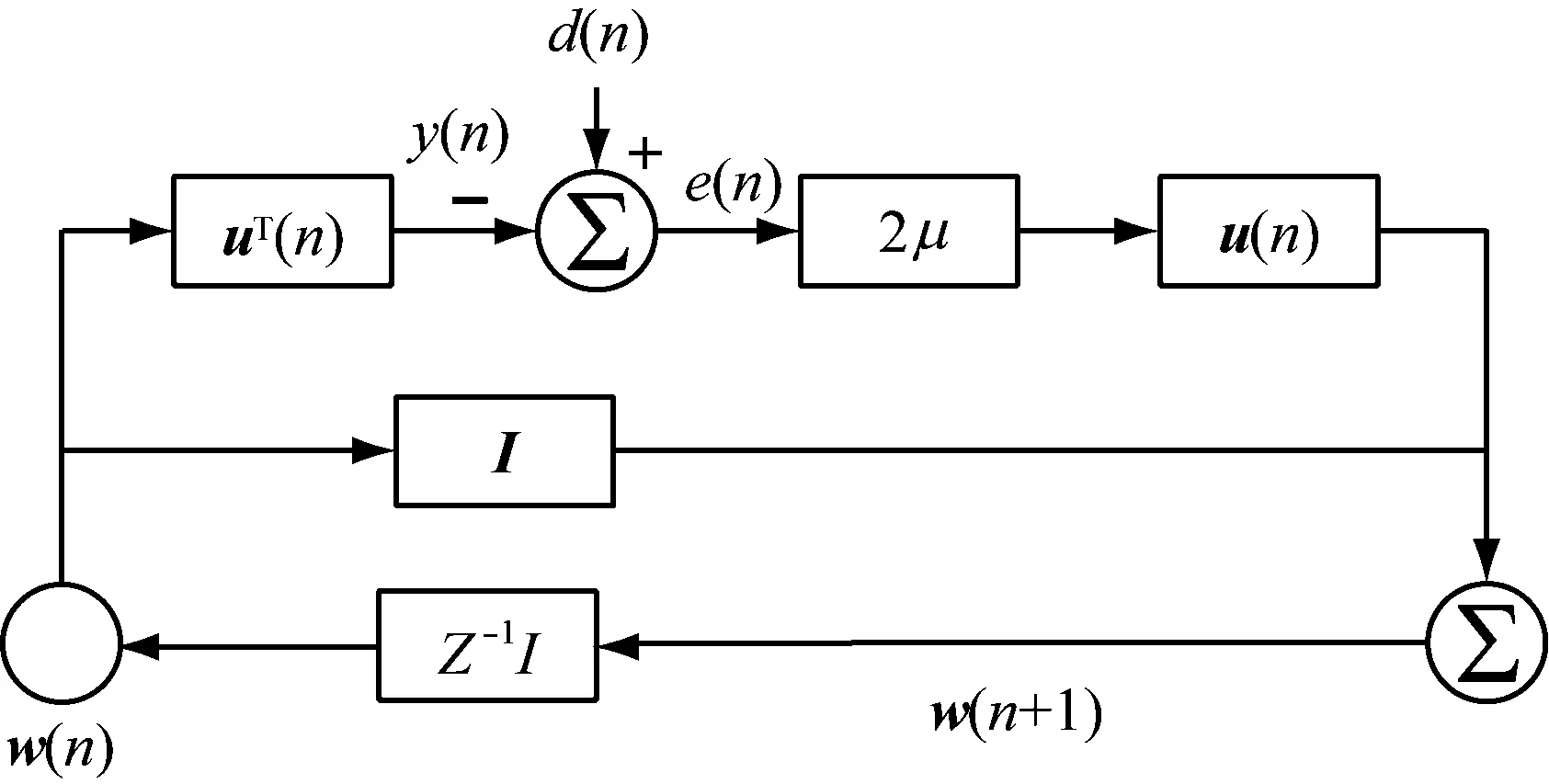
图2 自适应LMS算法结构图

由图2可知，误差

e(n)=d(n)-y(n)

将式(4)代入后得

e(n)=d(n)-WT(n)X(n)

(5)

则

e2(n)=d2(n)-2d(n)WT(n)X(n)+
WT(n)X(n)XT(n)W(n)

(6)

对其取数学期望后得

E[e2(n)]=E[d2(n)]-2E[d(n)XT(n)]WT(n)+
WT(n)E[X(n)XT(n)]W(n)

(7)

式中，E[d2(n)]、E[X(n)XT(n)]均为常数。

令WT(n)为变量x，则满足

E[e2(n)] =E[d2(n)]-2E[d(n)XT(n)]x+
E[X(n)XT(n)]x2(8)

式(8)为二阶函数，且为开口向上的抛物线曲线，函数存在最小值，故只需求出最小误差值就可以得到近乎所有的谐波含量。

只需对式(8)中的变量x进行一阶求导，得

时，最小误差值为

(9)

令ε(n)=E[e2(n)],由最速下降公式[15]

w(n+1)=w(n)-Kz(n)

其中，K为误差系数，z(n)为第n次时的误差，可得自适应LMS谐波检测算法的权值为

(10)

(11)

将式(5)代入式(11)，得

(12)

为了计算简便，可令ε(n)=e2(n)，则得到瞬时梯度的估计量为

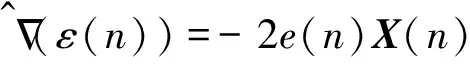
故有

w(n+1)=w(n)+2μe(n)X(n)

(13)

式中,μ控制着自适应LMS谐波检测算法的收敛速度和稳态误差，μ越大，收敛速度越大，且误差越大。

由图2可知，自适应LMS算法的权矢量w(n)只与输入数据u(n)有关，故当u(n)独立时，w(n)也是独立的。为获取μ的取值范围，计算LMS算法梯度估计的数学期望为

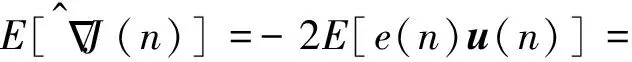
-2E[d(n)u(n)-u(n)uT(n)w(n)]=

(14)

式中，R为滤波器输入向量的相关矩阵；P为滤波器的输入与期望响应互相关向量

E[w(n)]-μ{RE[w(n)]-P}=

(I-μR)E[w(n)]-μP

(15)

由矩阵定义得，收敛因子的收敛范围满足

0<μ<1/tr(R)

(16)

式中,tr(R)为矩阵R的迹，即等于矩阵中主对角线元素之和。

3 仿真分析

为了验证本文方法具有更高的精确性与更好的实时性，本文利用MATLAB软件对自适应LMS谐波电流检测法与传统的瞬时无功功率p-q谐波电流检测法进行仿真比较。

(1)p-q谐波电流检测。瞬时无功功率中的p-q谐波检测法因其结构简单，动态响应快的特点而被广泛应用[16]。该方法可以将电路中的电流分解为有功和无功电流，便于对谐波电流进行计算。图3给出了利用p-q谐波电流检测法检测出的结果。

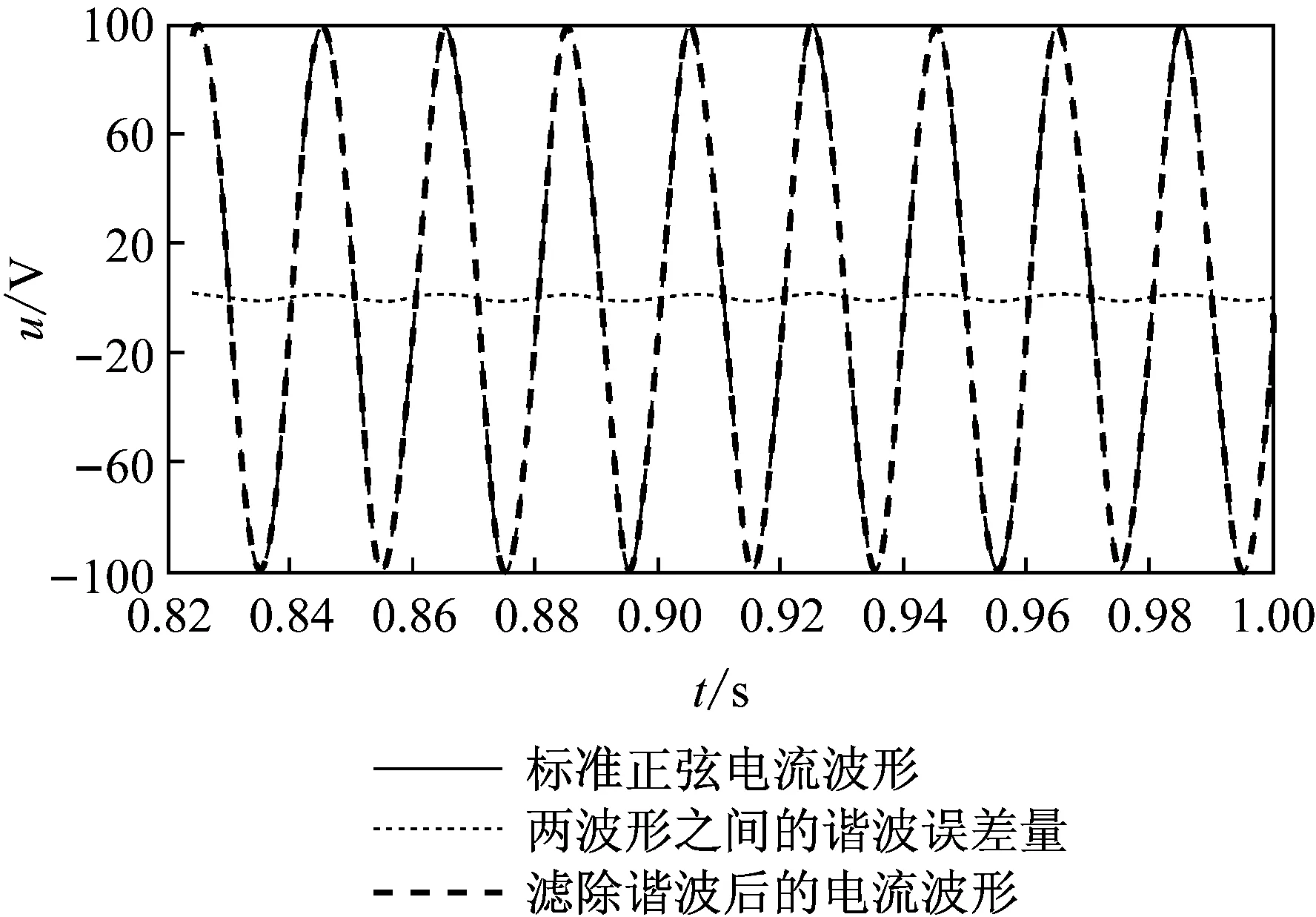
图3 p-q法谐波电流检测结果

由图3可见，利用p-q法滤除电流中的谐波含量后，与标准正弦电流信号相比，电流中仍然含有较多的谐波量，误差较大。可见，p-q法对误差无法进行自行调整，而且随着电路负载的变化，谐波量也会相应变化，无法精确地检测出电路中的实际谐波量。

(2) 自适应LMS谐波检测法。为验证本文中自适应LMS谐波检测法的效果，在标准正弦信号中加入随机噪声，形成含谐波的待检测电流信号；再使用本文方法检测并滤除该合成电流信号中的谐波,将滤除谐波后的信号与标准正弦信号对比较，即可得知检测的谐波是否完整。自适应LMS谐波检测算法流程如图4所示。

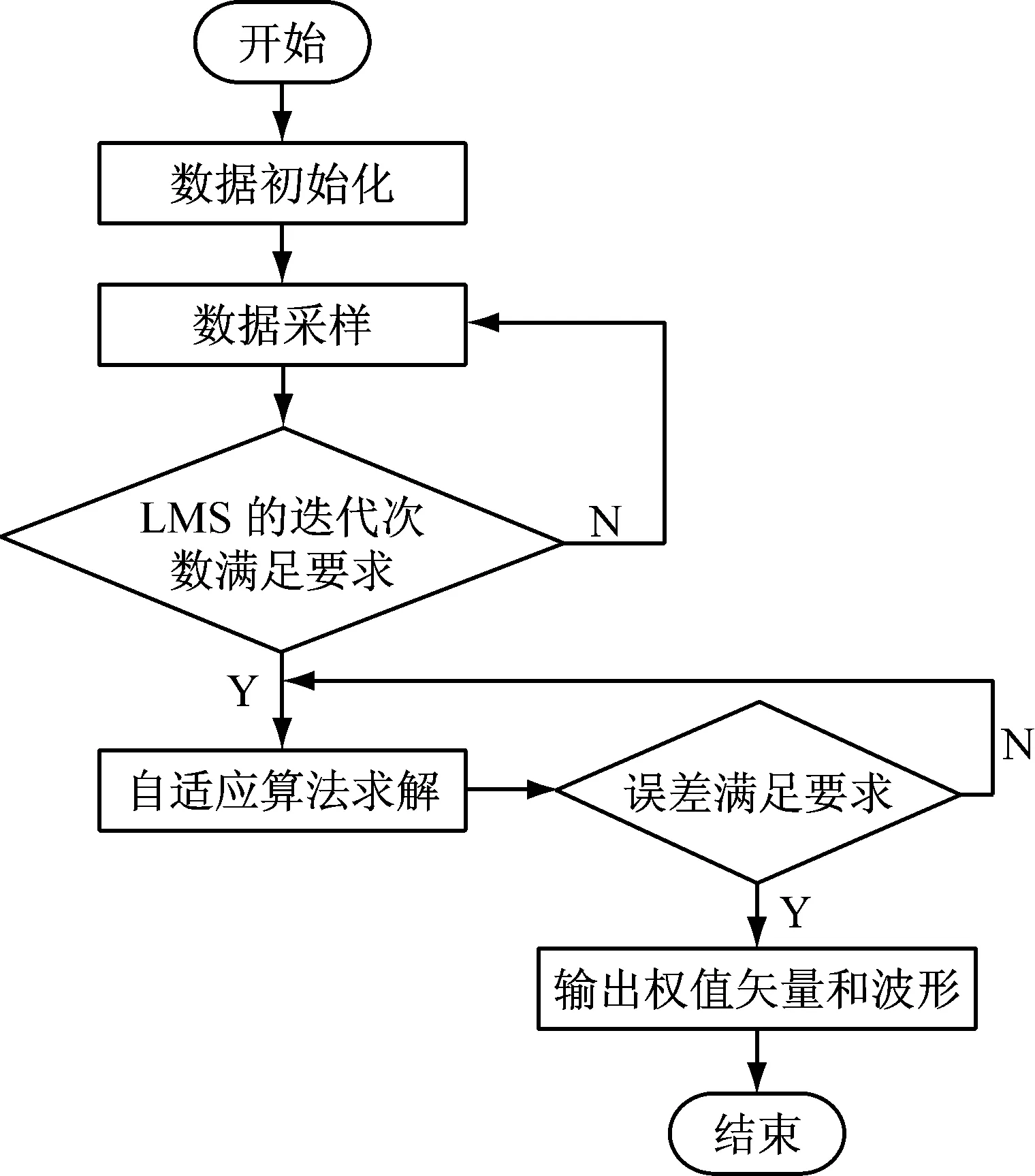
图4 自适应LMS谐波电流检测算法流程图

图5所示为用MATLAB软件产生的100s随机噪声信号，用来模拟电网或其他电力系统中的电流谐波成分，然后将随机噪声信号与标准正弦周期信号叠加，生成电路中包含谐波成分的待检测电流。

图5 噪声波形

图6给出了利用自适应LMS谐波电流检测法对待检测电流检测的结果。由图6可见，经过自适应滤波器滤除谐波后的电流信号不断地逼近滤除谐波后的电流波形；两波形之间的误差也在不断减小，误差逐渐地接近于一条直线，这间接地说明，检测出的谐波量也更接近于实际电路中的谐波量，谐波检测率高。可见，与传统的瞬时无功功率p-q谐波电流检测法相比，自适应LMS谐波电流检测法谐波检测的精确性更高。

图6 自适应LMS谐波电流检测结果

为分析收敛因子μ对滤波器性能的影响。图7给出了μ=10-3和μ=10-4时自适应LMS电流信号输出与滤除谐波后电流信号输出的误差。由图可见，信号的收敛速度与收敛因子μ的取值有关，不同的收敛因子对滤波器的性能有很大影响。图7(a)中，开始时滤波器的初始参数具有任意性，自适应LMS输出信号与滤除谐波后输出信号相差较大，但经过不断修正，当n=1 000时，自适应LMS滤波器电流信号输出已经实现了对滤除谐波后电流信号输出的精确逼近；图7(b)中,当n=8 000时，自适应LMS输出信号才接近谐波电流信号，自适应谐波检测速度慢，无法快速地在短时间内完成收敛。

图8给出了μ=10-3时自适应LMS谐波电流检测结果。与图6比较后发现，保持误差量e(n)和输入矢量X(n)不变，仅增大收敛因子μ的值，可使自适应LMS的谐波检测速度明显提高，也快速地达到了谐波的最佳状态，并在此状态下继续进行检测，最终使误差值不断趋向于零。

综上所述，分别对瞬时无功功率理论中p-q法和自适应LMS谐波检测法进行仿真，两者比较后发现，p-q法对于不断变化的负载电流的检测能力较差，无法对误差进行不断自我调整，误差大；自适应LMS谐波算法的检测结果更加逼近于电路的实际谐波电流量，而且增加收敛因子值后，检测速度更快，精度更高。

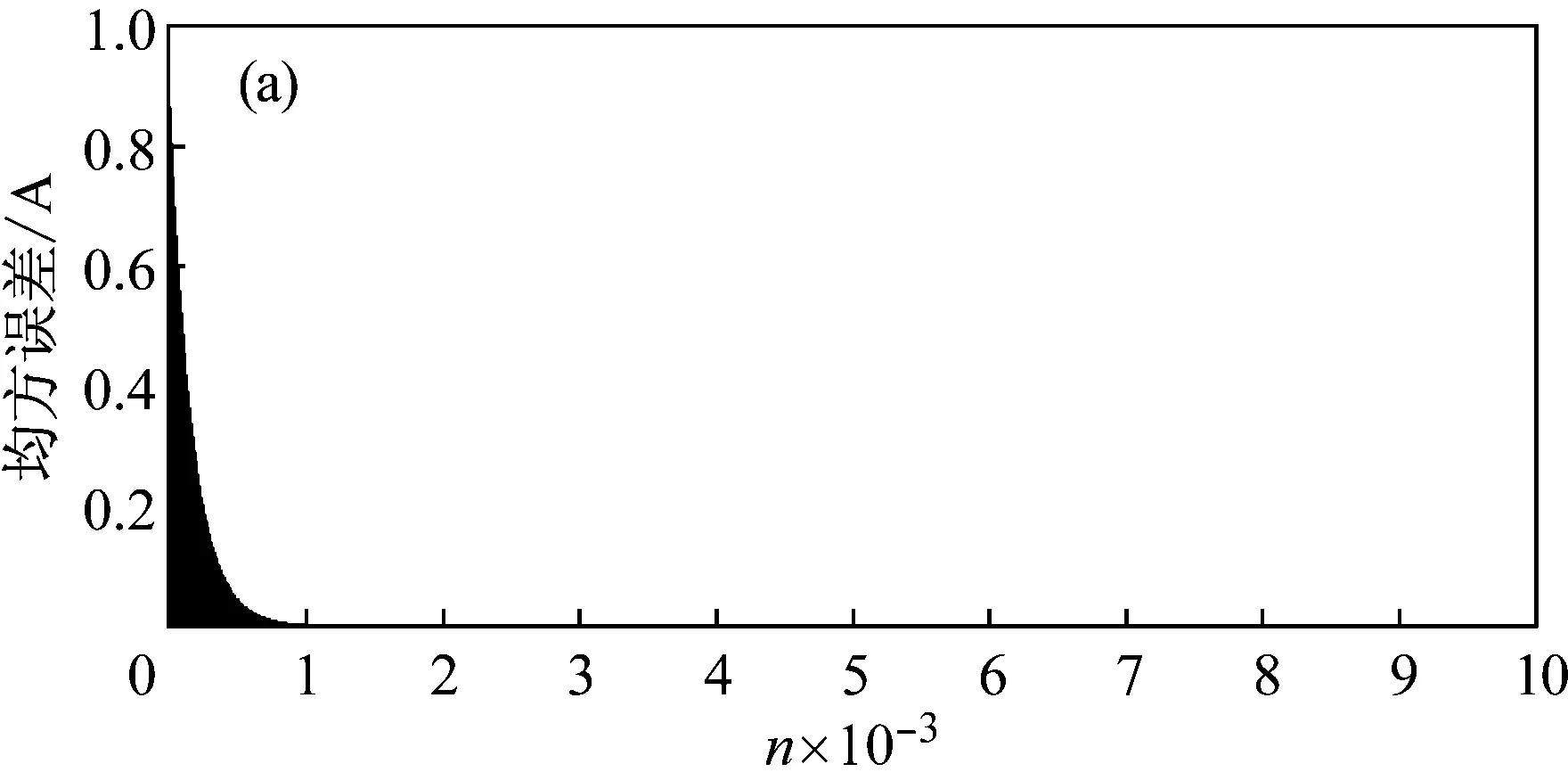
图7 μ=10-3和μ=10-4时，自适应LMS电流信号输出与滤除谐波后电流信号输出的误差

图8 μ=10-3时，自适应LMS谐波电流检测结果

4 结 语

谐波检测是有源滤波器中必不可少的一部分，谐波检测方法决定着电力系统和电力电子设备的滤波效果。本文研究了一种自适应LMS谐波检测法，它由程序中的循环部分不断地对参数进行修正，使之逼近主电路中实际所含的谐波量；同时，由于收敛因子μ决定着信号收敛速度和稳定性，通过调整收敛因子加快了算法的收敛速度，缩短计算时间，及时消除谐波。最后用MATLAB仿真验证了自适应LMS谐波检测算法的精确性和实时性。

[1] 罗皓文.有源电力滤波器指定次谐波检测与抑制技术研究 [D].武汉： 湖北工业大学，2013： 2-5.

[2] AKAGI H,KANAZAWA Y,NABAE A.Generalized theroy of the instantaneous reactive power in three-phase circuits [J].IPEC,1983： 1375-1386.

[3] 何英杰,刘进军,王兆安,等.一种基于瞬时无功功率理论的数字谐波检测 [J].电工技术学报，2010，25(8)： 185-192.

[4] 杨浩,叶明佳.d-q坐标变换的改进型谐波和无功电流检测法 [J].电源技术，2014，38(1)： 103-105，115.

[5] 吉晓青.有源电力滤波器的谐波检测及控制算法的研究 [D].保定： 河北大学，2015： 13-20.

[6] 盘洪斌,罗安,唐杰，等.一种改进的基于最小二乘法的自适应谐波检测方法 [J].中国电机工程学报,2008，28(13)： 144-151.

[7] 牛俊萍.基于自适应算法的电力系统谐波检测分析[D].徐州： 中国矿业大学，2014： 25-30.

[8] 王群,吴宁,谢品芳.一种基于神经元的自适应谐波电流检测法 [J].电力系统自动化，1997,21(10)： 13-16.

[9] PEREIA R R,da SILVA C H,Da SILVA L E B,et al.Improving the convergence time of adaptive notch filters to harmonic detection [C]∥36th Annual Conference on IEEE Industrial Electronics Society.[S.l.]： IEEE,2010： 521-525.

[10] 曹斌芳.自适应噪声抵消技术的研究 [D].长沙： 湖南大学，2007： 22-41.

[11] 孟小猛.自适应滤波算法研究及应用 [D].北京： 北京邮电大学,2010.

[12] 殷桂梁,郭磊,李相男.基于自适应陷波器单相电路无功功率测量新方法 [J].南方电网技术，2013,7(3):85-88.

[13] 陈艳,朱勇,易克初.一种改进的自适应滤波器的原理与FPGA实现 [J].电子工程师，2004,30(7):47-49，60.

[14] 喻翌,赵海全,何正友.基于ANCT和Adaline两种自适应谐波电流检测模型的分析 [J].电力系统保护和控制,2013，41(16)： 71-77.

[15] 宗荣芳,李丰林.最速下降与共轭梯度在数字波束形成中的研究 [J].计算机工程与应用，2010,46(19)： 151-153.

[16] 王兆安,李民,卓放.三相电路瞬时无功功率理论的研究 [J].电工技术学报,1992(3)： 55-59.

Harmonic Current Detection for Active Power Filter

XUPenghui,XUFei

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306)

To filter out harmonics in a circuit, harmonic components in the circuit should be detected accurately. This paper proposes an adaptive least mean square (LMS) harmonic current detection algorithm. A low-pass filter is replaced with an adaptive filter to solve the problem of real-time harmonic detection. The adaptive LMS harmonic current detection algorithm is used for grid voltage distortion. As frequency fluctuation of power parameters has good adaptive ability, it can be applied to three-phase or single-phase circuits. To change convergence factor of the algorithm, detection speed of harmonic can be accelerated. With MATLAB simulation, accuracy and real-time performance of the proposed algorithm is verified.

harmonic detection; self-adapting filter; least mean square; convergence factor

2016 -09 -26

徐鹏辉(1991-)，男，硕士生，主要研究方向为电力电子技术及其应用，E-mail： 1311697578@qq.com

2095 - 0020(2017)01 -0046 - 06

TM 933.1

A