基于K-means算法的RBF神经网络预测光伏电站短期出力

邵堃侠， 郭卫民， 杨 宁， 王 亮

(1.上海电力学院 自动化工程学院，上海 200090; 2. 国网河南省电力公司电力科学研究院，郑州 450052)

基于K-means算法的RBF神经网络预测光伏电站短期出力

邵堃侠1， 郭卫民2， 杨 宁1， 王 亮1

(1.上海电力学院 自动化工程学院，上海 200090; 2. 国网河南省电力公司电力科学研究院，郑州 450052)

对K-means算法加以改进，使用减法聚类确定聚类中心数量；以相距最远的两个样本作为聚类中心的边界，改进的K-means算法将K个初始中心分散到含有输入样本点的各个区域中，使其能够反映样本之间的关系和分布特征；初始中心确定后，使用点对称距离方法调整聚类中心。利用改进的K-means算法将历史日聚类分成4种天气类型，取相似日作为训练样本，对4种天气类型分别建立基于改进K-means算法的RBF神经网络功率预测模型。采用上海某光伏电站实测数据验证，结果表明提出的的预测方法精度提高，实用性较强。

功率预测； 径向基神经网络； K-means算法； 减法聚类； 点对称距离

近年来日益严重的环境问题使得越来越多的国家开始鼓励实施能源政策，促使可再生能源在能源市场所占比例日益攀升[1]。在众多电力系统中，光伏发电因其经济效益和环境效益受到高度重视。由于光伏电池成本逐渐下降以及相关技术日趋成熟[2]。2015年，全球范围内光伏装机容量新增近50 GW，与2014年同比增长25%，累计装机容量近230 GW；中国、日本和美国继续占据着最大市场，占新增装机容量的2/3[3]。

能源互联网是能源与互联网相互融合的产物，它的建立将大力推进可再生能源的消纳，促进光伏产业的发展。然而，并网光伏发电装机容量迅速壮大，其发电波动对电力系统造成的冲击直接影响电网运行的可靠性与稳定性[4]，使得新增发电量无法通过现有电网消纳，由此引发的“弃光限电”现象制约了光伏电站的建设。为降低光伏发电对电力系统的冲击，需对光伏出力进行短期预测。光伏发电系统短期功率预测是指利用一种或几种有效的方法，对光伏发电系统的有功功率进行1～2 d的预测[5]。高效的出力预测对有效利用光伏发电、提高清洁能源的利用率必不可少。

光伏发电功率预测方法可分为间接预测和直接预测两类[6]。直接预测是直接对光伏电站的输出功率进行预测；间接预测则先对地表辐照强度进行预测,然后根据光伏电站出力模型得到光伏电站的输出功率[7]。文献[8]中将专业天气预报的33种天气类型分为4类广义天气类型，利用支持向量机完成天气类型识别，实现了缺失天气类型信息的历史数据的辨识恢复，确保了其完整性和可用性。总结各类气象因素对光伏出力的影响，文献[9-10]中建立了基于神经网络的光伏系统短期出力预测模型，具有较好的实用性和可行性。

由于在具有相似气象条件的情况下，光伏阵列的输出功率曲线具有一定的相似度，故可以通过选取相似日进行功率预测[11]。本文将相同天气类型的相似日作为训练样本，建立基于K-means算法的径向基(Radical Basis Function, RBF)神经网络预测模型，利用上海某光伏电站历史数据及当地天气预报数据进行验证，预测结果表明本文提出的预测模型性能较高。

1 RBF神经网络

RBF神经网络结构简单、学习能力快，被广泛应用于函数逼近、模式分类与识别中。其可以任意精度逼近任意的非线性函数，具有全局逼近能力，从根本上解决了BP神经网络的局部最优问题，且拓扑结构紧凑，结构参数可实现分离学习，收敛速度快[12]。

RBF神经网络由输入层、隐含层和输出层组成，其结构如图1所示。其中，网络的输入矩阵X=(x1,x2,…,xN)，N为样本总数，p=1，2，…，N；wkm为隐含层第k个节点到输出层第m个节点间的连接权值，k=1,2,…,K，K为隐含层节点数，m=1,2,…,M，M为输出层节点数；ym为与输入样本对应的第m个输出层的实际输出；Y=(y1,y2,…,yM)T为网络的输出。

RBF神经网络中，隐含层神经元的输出常由高斯函数产生[12]：

(1)

由图1所示的RBF神经网络的结构可以得到网络输出为

(2)

设d为样本的期望输出值，基函数的方差为

(3)

RBF神经网络的学习过程如下:确定隐含层基函数中心与方差，为无导师学习阶段，即根据输入大量的数据，总结提炼找到规律和模式，自动调整拓扑结构和权值，经过不断调节使其结构具有适应需求的特性；计算隐含层与输出层的连接权值，为有导师学习阶段，即将一组训练集送入网络，根据网络的实际输出与期望输出间的差别来调整连接权。通常，利用K-means算法调整中心向量，学习算法具体步骤如下[12]：

(1) 基于传统K-means算法求取基函数中心ck。K-means是一种无监督聚类算法，由MacQueen[13]在1967年提出，主要用于分析和观测数据。该算法先随机选择K个输入样本作为初始聚类中心，K即隐含层的节点数，计算样本xp与ck间的欧氏距离，并将该样本分配到最邻近的聚类集合γk中，取γk中各样本的平均值作为新的中心。重复上述过程，直至相邻两次计算中聚类中心没有发生改变，则ck为RBF神经网络基函数中心。

(2) 求解方差

(4)

式中，dc_max为聚类中心之间的最大距离。

(3) 用最小二乘法调节隐含层与输出层之间的连接权，

(5)

2 改进的K-means算法

本文利用K-means算法确定RBF神经网络隐含层中心。K-means算法具有以下特点[14]：① 对于大数据集处理，效率高且相对可伸缩；② 易陷入局部最优解；③ 一般只能发现球状簇；④ 聚类个数K需预先给定，且对预先指定的初始簇的选择很敏感。本文利用减法聚类确定K，定义两个相距最远的输入样本为初始聚类中心的边界条件，并给出确定初始聚类中心的方法；K-means算法利用欧氏距离作为相似性度量，难以发现非凸形状的簇或差异较大的簇，故本文利用点对称距离更新聚类中心。

2.1 减法聚类

减法聚类是一种简单、有效的聚类算法[15]，它将各样本点当作可能的聚类中心，按照样本点的密度指标确定聚类中心。该算法可以自动确定聚类数，并且能有效反映数据的分布情况。减法聚类的过程如下[16]：

(1) 已知N个处于N0维空间内的数据样本，则每个数据点密度为

(6)

式中，p和p′分别为第p个和第p′个数据样本；γa为常数。若该点密度较大，则与该点相邻的样本点较多。

(2) 按照式(6)计算各样本点的密度，密度最高的点定义为第1个聚类中心c1，其密度指标为Dc1；此时，k=1，更新各样本点的密度指标，即

(7)

式中，ck为第k个聚类中心；Dck为第k个聚类中心的密度指标；γb为参数。

对于减法聚类中的参数γa和γb，文献[15]中提出了一种确定方法[17]，即取

(8)

此处γa、γb表示处于样本集合最中间的样本到距离它最远的样本之间距离的1/2。

(3) 按照式(7)修正各样本点的密度指标，确定Dmax=max(Dp)，选定下一个聚类中心c2。若满足

Dmax/Dc1<δ

(9)

则迭代结束，聚类个数K=k；否则，K=k+1，并将密度指标最高的样本点作为第k个聚类中心，重新计算式(7)，确定新的Dmax。其中，δ<1为给定的参数，当δ≥0.5时会取得较好效果[18]，本文取δ=0.5。

2.2 点对称距离

传统的K-means算法使用欧氏距离定义样本之间的相似性，欧氏距离可以检测到球形簇，但是不能检测到主轴附近的集群。为克服上述缺点，本文采用文献[19]中提出的“点对称距离”定义样本之间的相似性，具体如下：给定N个样本，参考点c(这里指一个聚类中心)，样本被分配到点对称距离最小的聚类中，样本sq与参考点c之间的点对称的距离为

(10)

2.3 改进的K-means算法

本文对K-means算法的改进分为两步：

(1) 确定聚类中心数K。利用上文所述的减法聚类确定K，即RBF神经网络的隐含层中心点数K。

(2) 确定初始聚类中心，利用点对称距离计算聚类中心。

选出输入样本中欧氏距离最大的两个样本xmax_p和xmax_p′，将两者之间欧氏距离dmax平均分为(K-1)个子区间，则每个间距为

d=dmax/(K-1)

假设在所有输入样本中，有n1个样本到xmax_p的距离小于等于d/2 ，取C1为这n1个输入样本的平均值，即

(11)

假设在所有输入样本中，有nK个样本到xmax_p′的距离小于等于d/2 ，取CK为这nK个输入样本的平均值，即

(12)

为把聚类中心分配到输入样本所在的各区域中，设两个相邻中心之间的最小距离dc=1.5d。

设ds(xp,Ck)为xp和Ck之间的点对称距离，其取最小值时的k为xp所属的聚类簇；H(k)为k类样本的数目,取Ck所在的簇内所有样本的平均值为xavg，相邻两次迭代中聚类中心的总均方误差为Mse。图2给出了聚类中心的计算流程图。

初始中心确定后，使用点对称距离方法调整聚类中心，当相邻两次迭代的聚类中心没有发生明显改变时，迭代终止，得到最终的聚类中心。

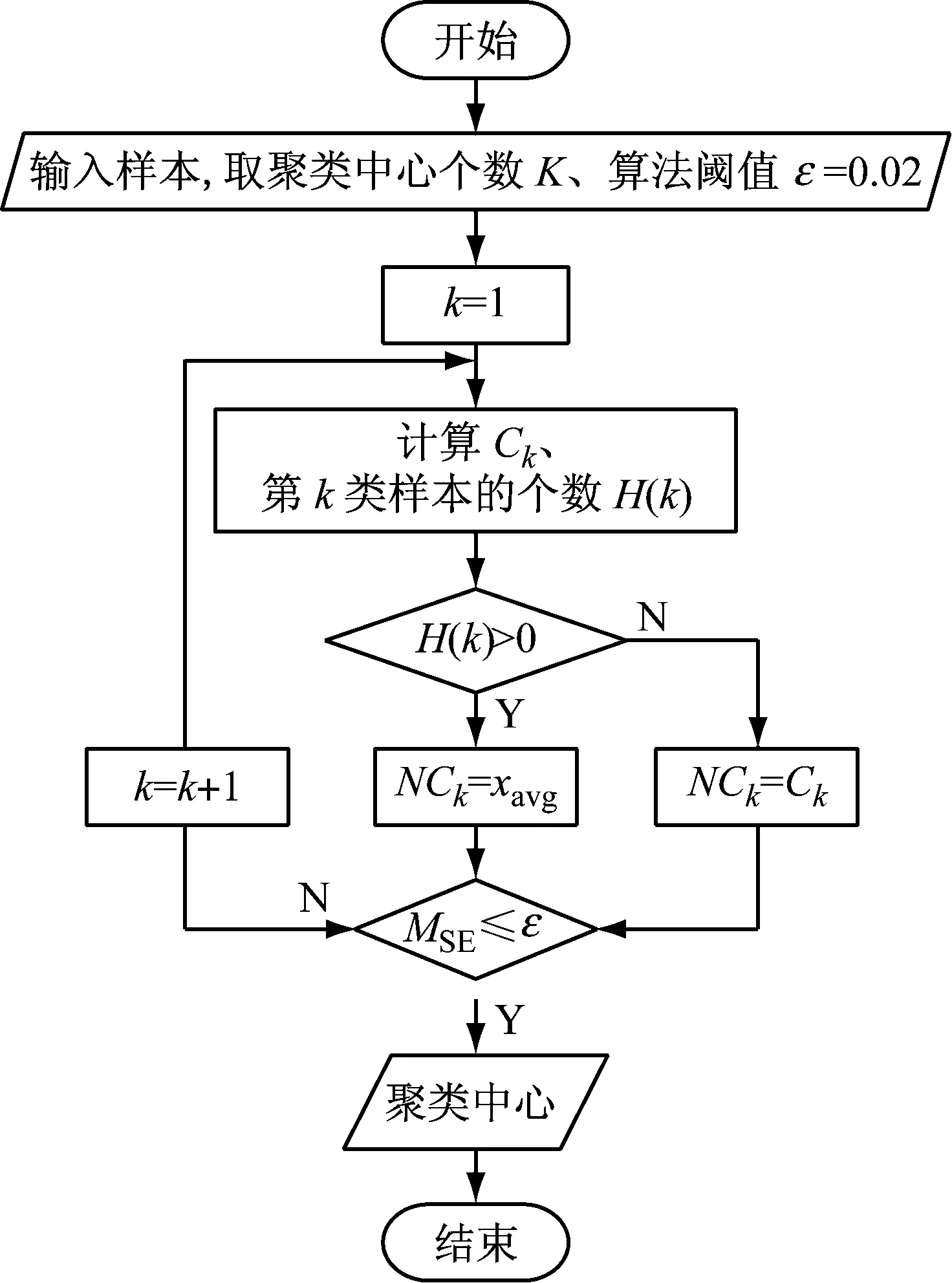
图2 聚类中心的计算流程图

Fig.2 Flow chart of cluster center

3 预测模型设计

3.1 影响光伏发电功率的主要因素分析

光伏发电出力主要取决于太阳辐射总量对光伏面板的影响[20]，同时，温度、湿度等气象因素也不能忽视。实际工程中，可粗略估计光伏发电系统的输出功率为[21]

P=ηSI[1-0.005(t0+25)]

(13)

式中，η为光电转换效率，%；S为光伏阵列总面积，m2；I为接收到的太阳光照强度，kW/m2；t0为大气温度，℃。

由式(13)可知，影响光伏出力的主要因素为太阳光照强度、大气温度、光伏阵列的总面积和转换效率等。对于确定的光伏电站，S、η都已包含在光伏阵列的历史发电序列中，但是，不同天气类型下太阳辐射的波动和气温的变化对光伏出力的影响也不可忽视。因此，本文取天气类型、大气温度和光照强度作为影响光伏出力的主要因素。

3.2 相似日选取原理

考虑到光伏电站每天6:00—17:59 可能有功率输出，定义6:00—17:59 各整点为基值点，故输入变量为12个基值点对应的温度值，输出为预测日各基值点光伏阵列的输出功率。RBF神经网络是单隐含层结构，隐含层节点数根据实际情况增减。本文中，传统的K-means算法的隐含层节点数K根据经验法确定；改进的K-means算法中，使用减法聚类确定K值。

光伏发电出力受不同天气类型下太阳光照强度的影响，利用历史天气数据将历史日分为文献[8]中所述的A、B、C、D 4类广义天气类型(见表1)。为了体现光照强度对发电量的影响，利用改进的K-means算法，按照光照强度将历史日的专业气象天气类型重新按表1中的4类广义天气类型进行分类，然后，针对不同的天气类型建立各自对应的预测模型。

表1 广义天气类型对应表

选择预测日前30 d中与预测日天气类型相同的历史数据集Q1，分别计算Q1中历史日与预测日温度的欧氏距离diT，取diT较小的6 d作为该预测模型的相似日集Q2，即

(14)

式中，TiTnT为第iT个历史日第nT个温度值；TnT为预测日的第nT个温度值；NT为温度值个数。

3.3 RBF神经网络的训练

确定预测模型的结构后，将相似日集Q2作为训练样本，并根据预测误差调整网络参数；利用预测日的样本作为测试集，测试网络的预测效果，并对预测模型进行改进和优化。RBF神经网络的训练步骤如下：

(1) 对输入数据进行预处理。筛选历史日样本，剔除奇异数据；为防止神经元出现饱和现象，对样本数据归一化处理，使其介于[0，1]之间，即

(15)

式中，vi为归一化后的样本点；Vi为第i个样本点；Vmin和Vmax分别为对应历史数据的最小值和最大值。

预测值y为归一化后通过RBF神经网络模型得到的预测数据，是介于[0，1]的值，需对y进行反归一化，转化为实际预测值Y，即

Y=y(Ymax-Ymin)+Ymin

(16)

式中，Ymin和Ymax分别为历史数据中发电功率的最小值和最大值。

(2) 进行预测时，相似日集D2作为预测模型的训练样本。

4 实验分析

本文以上海某光伏电站2015年3—5月历史发电数据及当地同时间的气象数据为例，使用Matlab 2013a进行仿真。选取与A、B、C、D类4种广义天气类型相对应的5月22日、5月26日、5月17日、5月30日作为预测日。为验证本文方法的有效性，利用传统K-means算法建立了RBF神经网络功率预测模型，记为模型1；利用本文提出的改进K-means算法建立了RBF神经网络功率预测模型，记为模型2；利用本文提出的改进K-means算法按照光照强度对历史数据分类，再建立的RBF神经网络功率预测模型，记为模型3，分别进行光伏电站发电功率预测。

图3给出了预测结果与实际发电功率的比较图。由图3可知，对于A类天气，3种模型的预测值与实际值都比较接近，预测效果较好，发电功率变化比较有规律；对于B类天气，某些时段的预测误差较大，这是由于阴云天气使一天中云层的厚薄和位置变化难以预测，云层造成的阴影对光伏电池阵列的输出影响较大，使得预测结果误差增大；对于C、D类天气，由于天气变化情况比较复杂，导致某些时段预测结果误差较大，但从结果可见，本文提出的方法预测结果更好。

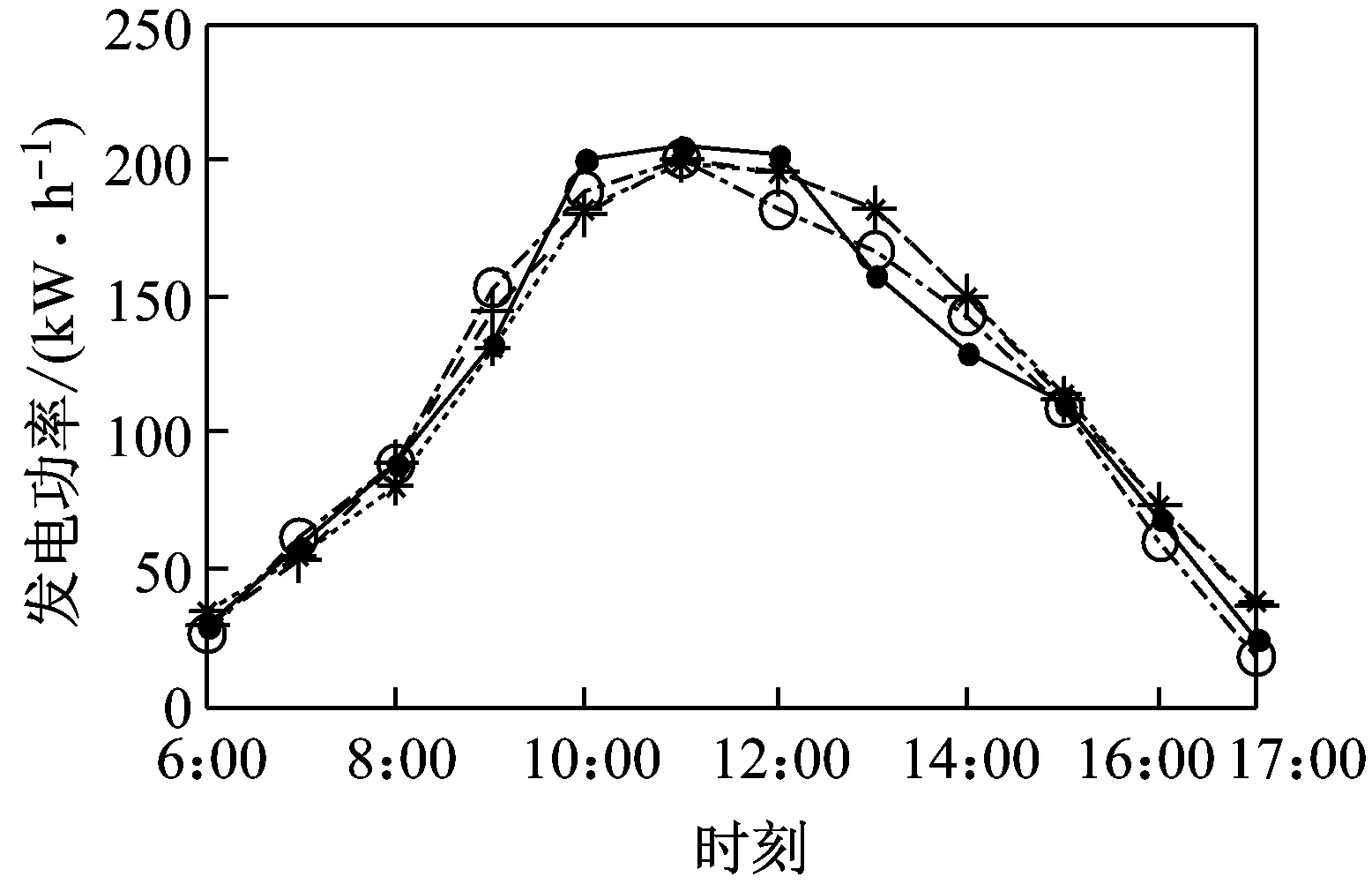
(a) A类天气(2015-05-22)

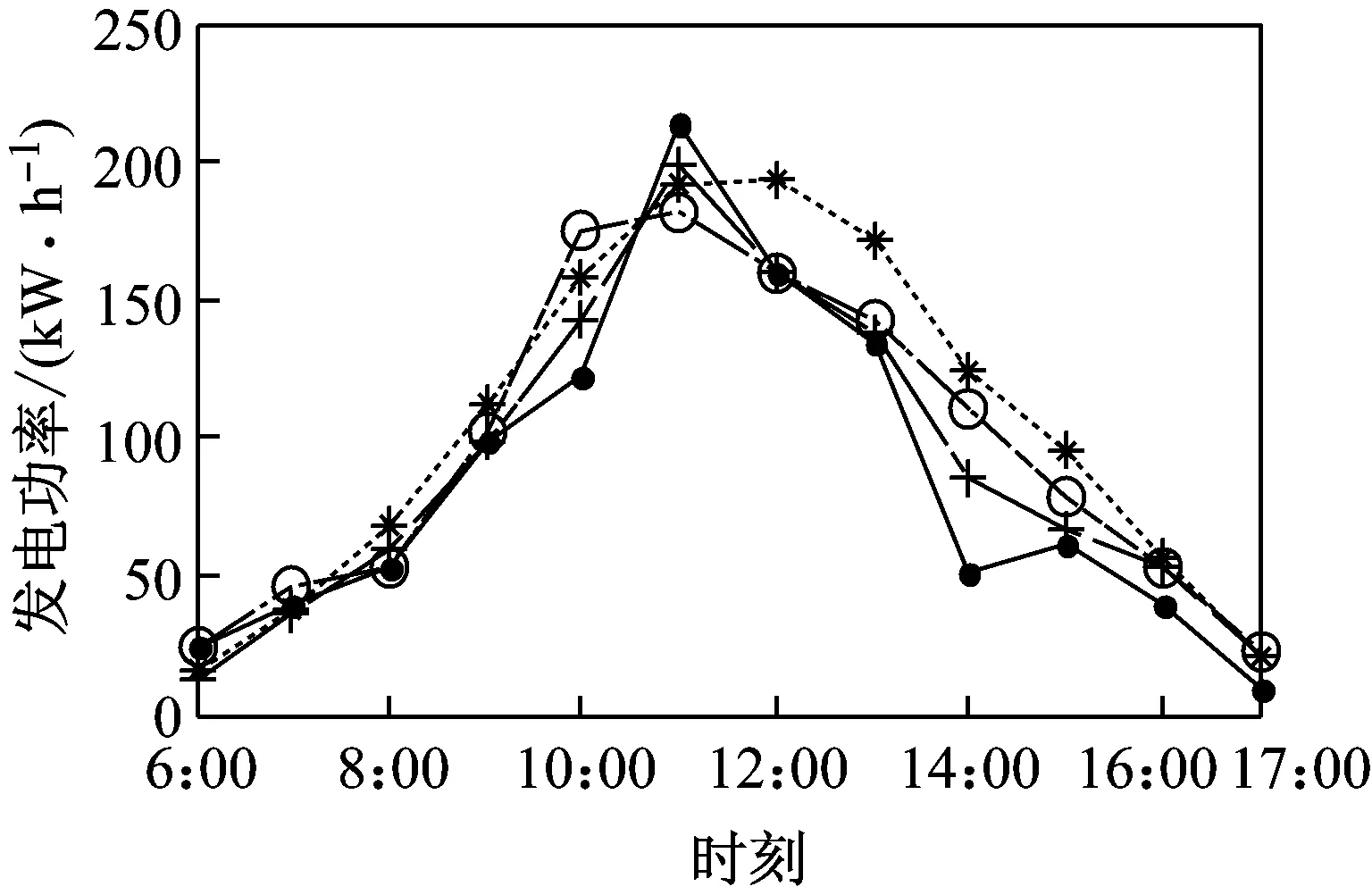
(b) B类天气(2015-05-26)

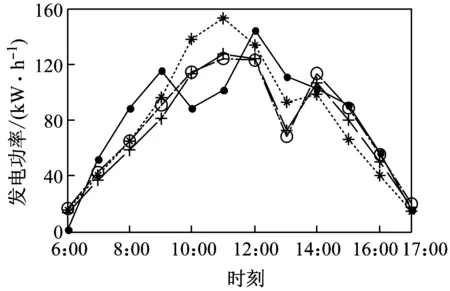
(c) C类天气(2015-05-17)

(d) D类天气(2015-05-30)

由于预测结果与实测值之间存在误差，需要对发电功率预测模型做出评估。本文采用平均绝对百分比误差[18](Mean Absolute Percentage Error，MAPE)和均方根误差[18](Root Mean Square Error，RMSE)作为预测模型的综合评价指标，如果误差值越低，说明预测模型的精度越高。

(17)

(18)

式中，PMi为第i个基值点实际功率；PPi为第i个基值点的预测功率；Cap为日平均开机容量，kW；M0为输出样本个数。

预测结果评估如表2所示。通过对比表中各模型的RMSE和MAPE值可知：模型3较模型1、2的预测精度都要高。 因此，本文提出的模型3可有效预测光伏系统输出功率，从而满足可再生能源系统的有效规划。

表2 各模型的预测结果评估

5 结 语

本文提出了一种确定RBF神经网络隐含层中心的算法：利用减法聚类自动确定隐含层中心数目，确定能够反映输入样本分布的初始聚类中心，最后利用点对称算法更新初始中心。利用本文提出的改进K-means算法将历史日按光照强度聚类分成4种类型，取相似日作为训练样本，建立基于K-means算法的RBF神经网络功率预测模型，并利用改进的K-means算法优化RBF神经网络预测模型。比较3个模型的预测结果可知，本文提出的预测模型性能较高，但是对于C和D类天气类型，预测精度还有待提高，这是由于这两类天气变化情况较复杂，某些时段可能出现较为明显的天气变化，导致预测结果误差较大。针对这种情况，可将这两类天气的数据划分时段，选取与预测日天气预报各时段天气类型分别相同的历史数据组成相似日作为训练样本。本文利用历史数据直接预测光伏发电功率，不需要复杂的建模和计算，适当增加训练样本数目并结合本文提出的预测模型3，可提高光伏电站发电功率的预测精度。

[1] RAZA M Q, NADARAJAH M, EKANAYAKE C. On recent advances in PV output power forecast [J]. Solar Energy, 2016, 136:125-144.

[2] CANDELISE C, WINSKEL M, GROSS R J K. The dynamics of solar PV costs and prices as a challenge for technology forecasting [J]. Renewable Sustainable Energy Reviews, 2013, 26: 96-107.

[3] International Energy Association Photovoltaic Power Systems Programme (IEA PVPS)．IEA PVPS annual report 2015 [EB/OL]. (2016-05-13)[2016-08-26].http://iea-pvps.org/index.php?id=6&eID=_frontend push & docID=3195.

[4] 陈炜,艾欣,吴涛,等.光伏并网发电系统对电网的影响研究综述 [J].电力自动化设备，2013,33(2):26-32，39.

[5] 杨德全. 基于神经网络的光伏发电系统发电功率预测 [D].北京: 华北电力大学, 2014：1.

[6] 丁明,王磊,毕锐.基于改进BP神经网络的光伏发电系统输出功率短期预测模型 [J].电力系统保护与控制，2012,40(11):93-99，148.

[7] 卢静,翟海青,刘纯,等.光伏发电功率预测统计方法研究 [J].华东电力，2010,38(4):563-567.

[8] 王飞. 并网型光伏电站发电功率预测方法与系统 [D].北京: 华北电力大学,2013.

[9] 张岚,张艳霞,郭嫦敏,等.基于神经网络的光伏系统发电功率预测 [J].中国电力，2010,43(9):75-78.

[10] MELLIT A, PAVAN A M. Performance prediction of 20 kWp grid-connected photovoltaic plant at Trieste(Italy) using artificial neural network [J]. Energy Conversion and Management, 2010,51(12): 2431-2441.

[11] 白俊良, 梅华威.改进相似度的模糊聚类算法在光伏阵列短期功率预测中的应用 [J].电力系统保护与控制, 2014，42(6):84-90.

[12] 周品. MATLAB神经网络设计与应用 [M].北京: 清华大学出版社,2013：232-237.

[13] MACQUEEN J. Some methods for classification and analysis of multivariate observations [C]// Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, Califor-nia: University of California Press, 1967,1: 281-297.

[14] VISALAKSHI N K, SUGUNA J. K-means clustering using Max-min distance measure [C]//2009 Annual Meeting of the North American Fuzzy Information Processing Society. Cincinnati, Ohio, USA: Nafips, 2009:1-6.

[15] 王洪斌,杨香兰,王洪瑞.一种改进的RBF神经网络学习算法 [J].系统工程与电子技术，2002,24(6):103-105.

[16] CHIU S L. Fuzzy model identification based on cluster estimation [J].Journal of Intelligent & Fuzzy Systems, 1994, 2(3):267-278.

[17] 裴继红,范九伦,谢维信.聚类中心的初始化方法[J].电子科学学刊，1999,21(3):320-325.

[18] PAL N R, CHAKRABORTY D. Mountain and subtractive clustering method: Improvements and generalizations [J].International Journal of Intelligent Systems,2000,15(4):329-341.

[19] SU Muchun, CHOU C H. A modified version of the K-means algorithm with a distance based on cluster symmetry [J].IEEE Transactions on Pattern Analysis & Machine Intelligence, 2001, 23(6):674-680.

[20] ANTONANZAS J, OSORIO N, ESCOBAR R, et al. Review of photovoltaic power forecasting[J]. Solar Energy, 2016, 136:78-111.

[21] YONA A, SENJYU T, FUNABASHI T. Application of recurrent neural network to short-term-ahead generating power forecasting for photovoltaic system[C]//IEEE Power Engineering Society General Mee-ting.Tampa, FL, USA: IEEE,2007: 1-6.

Short-term Forecasting for PV Power Generation Using RBF Neural Network Based on Improved K-means Algorithm

SHAOKunxia1，GUOWeimin2，YANGNing1，WANGLiang1

(1.College of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090， China; 2. Electric Power Research Institute of State Grid Henan Electric Power Company, Zhengzhou 450052, China)

This paper proposes an improved K-means algorithm. The number of clustering centers is determined by subtractive clustering. The farthest two samples are taken as the boundary of cluster centers. The improved algorithm aims to distribute theKinitial centers in each region of the input space to reflect the relationship and distribution characteristics of samples. A point symmetry distance measure is used to update the initial cluster centers. Historical data are divided into four types of weather using the improved K-means algorithm, and the data of similar days are used as training samples. Four prediction models are established based on the improved K-means algorithm. The results show that the proposed method has high performance and practicability, verified by the measured data of a PV power station in Shanghai.

power prediction; radical basis function (RBF) neural network; K-means algorithm; subtractive clustering; point symmetry distance

2016 -11 -21

上海市科委地方院校能力建设项目资助(15160500800)；分布式试验检验系统数据处理平台(H2015-159)

邵堃侠(1990-)，女，硕士生，主要研究方向为光伏发电功率预测，E-mail：shaokunxia@163.com

2095 - 0020(2017)01 -0027 - 07

TM 615

A