基于新型趋近律的船舶微网直流变换器控制策略

古龙瑞, 岑建军, 张勤进, 郭昊昊

(1.大连海事大学 轮机工程学院, 辽宁 大连 116026;2.中国铝业股份有限公司连城分公司, 兰州 730000)

基于新型趋近律的船舶微网直流变换器控制策略

古龙瑞1, 岑建军2, 张勤进1, 郭昊昊1

(1.大连海事大学 轮机工程学院, 辽宁 大连 116026;2.中国铝业股份有限公司连城分公司, 兰州 730000)

船舶微网中母线电压的稳定控制、功率负荷分配等问题一直是研究的热点。针对船舶直流变换器中等速趋近律控制方法趋近时间长、抖振严重的问题，提出了一种新型趋近律方法，用于改善系统的趋近状态和稳定性能。同时，将功率-电压下垂控制方法和新型趋近律控制器相结合，实现了船舶微网中直流变换器功率合理分配。仿真实验表明了所提控制策略的有效性。

船舶微电网； 新型趋近律； 直流变换器； 下垂控制； 鲁棒性

随着能源危机和环境污染等问题的加剧，分布式微电网技术的研究取得了丰富成果[1-3]。微电网主要分为交流微电网和直流微电网。与交流微电网相比，直流微电网由于结构简单、能源利用效率高、控制简单等特点在船舶领域等得到了广泛应用[3-5]。

直流微电网系统中，可再生能源输出的不稳定性会降低了系统动态性能，对供电质量产生较大的影响。目前，针对微电网中直流变换器的控制策略研究已有不少进展[1-12]。文献[6]中考虑了寄生电阻和电感电流纹波对系统动态性能的影响，基于峰值电流模式控制建立了直流变换器小信号交流模型，保证了系统稳态工作性能。但是，小信号模型无法全面揭示变换器在整个工作区内的稳定信息，在大信号扰动时系统会不稳定。为了寻求精确的控制器设计方案，一些学者将滑模控制引入到直流变换器的控制中。文献[7]中针对新能源发电中输入、输出端存在的大扰动问题，基于Super-Twisting 高阶滑模控制算法设计了Buck-Boost变换器的滑模控制器，有效地削弱了传统滑模固有的抖振现象，提高了系统大扰动时的动态系统。但是，高阶滑模控制算法参数较多，设计控制器十分复杂。文献[8-9]中将滑模控制器应用于直流变换器，获得了良好的稳定性和鲁棒性。上述研究都针对单个直流变换器稳定性策略研究，并未对并联均流控制策略进行分析。文献[10-11]中提出了一种基于阻性虚拟阻抗加补偿虚拟阻抗的下垂控制策略，用于实现多个直流变换器并联时功率分配的问题，其中阻性虚拟阻抗实现直流微电网稳态时的功率分配，补偿虚拟阻抗提升其动态性能。但是，补偿虚拟阻抗并不能完全补偿由于下垂特性引起的母线电压跌落问题。

本文针对船舶直流变换器中等速趋近律控制方法趋近时间长、抖振严重的问题，提出了一种新型趋近律，用于提高系统在趋近运动阶段的趋近速度以及抑制滑模运动阶段的抖振现象，并与等速趋近律进行了对比分析。经分析可知，提出的趋近律趋近时间短，且能有效抑制滑模控制固有的抖振问题。以输出电压误差和电压误差变化量作为系统状态变量，得到直流变换器的动态模型。在此基础上，基于新型趋近律设计了直流变换器的控制器，并将功率-电压下垂原理和新型滑模控制器相结合，对直流变换器的并联均流进行了研究。仿真结果表明了理论分析的正确性。

1 直流变换器数学模型

以船舶直流微电网中常用的Buck变换器(降压变换器)为例进行详细分析，其分析过程同样适用于其他类型直流变换器。

图1为Buck变换器的拓扑结构图，它是由输入电压Ug、功率开关器件S、二极管D、储能电感L、滤波电容C以及负载R组成；U0为母线电压。

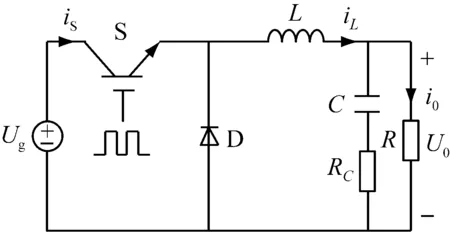
图1 Buck变换器拓扑结构图

Buck变换器通过功率开关器件S的快速通断，以维持输出电压的稳定。调节功率开关器件S的通断周期，即可调整输出电流和电压的大小。假设负载为阻性负载，以电感电流iL与电容电压uC为状态变量，忽略电感和电容的寄生参数，可得Buck变换器的状态空间方程为

(1)

式中,ui为输入电压瞬态值;us为状态变量,us=1时,功率开关器件S导通；us=0时,功率开关器件S关断。

2 等速趋近律和新型趋近律的对比

文献[13]中利用趋近律概念来降低切换函数在滑模面附近的变化率，实现变结构的快速切换，从而有效地抑制了抖振水平。

2.1 等速趋近律趋紧时间与抖振分析

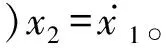
(2)

选择线性滑模切换面为

s(x)=ax1+x2

(3)

式中，α为滑模面参数。

利用等速趋近律设计Buck变换器滑模控制器，其趋近律为

(4)

式中,k1为常数，表示趋近切换面s时的速率。

通过调整k1可调整趋近速度，当k1增大时，趋近滑模平面的速度越大；减小k1，则趋近滑模平面的速度相应减小。

结合式(2)～(4)，可以得到等速趋近律下控制器的输出函数为

(5)

由式(5)可知，其包含不连续项k1b-1sgn(s);该不连续项是导致滑模抖振问题的本质原因,且抖振水平与k1直接相关。

通过对式(4)两边同时积分可推导出,在等速趋近律作用下趋近滑模切换面所需时间为

(6)

根据式(6)可知，等速趋近律的趋近时间t1可以通过k1进行调节。当k1增大时，则趋近速度增加,系统的趋近时间缩短。然而，由式(5)可知，k1增加，将导致控制器的输出抖振水平也相应增大。因此，对于等速趋近律而言，趋近速度与抖振水平是相互矛盾的；为了解决这一本质上的矛盾，在等速趋近律的基础上给出一种新型趋近律。

2.2 新型趋近律的提出与分析

本文提出的新型趋近律的具体形式为

(7)

式中,k>0;0<ε<1;η>1;δ>0;x1为系统状态变量;eq(·)为函数。

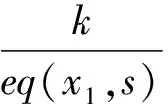
对式(7)进行整理，有

-ksgn(s)

(8)

对式(8)两边从0～t进行积分，则该新型趋近律趋近滑模切换面所需要的时间为

(9)

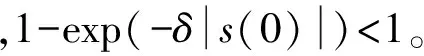
t<ε|s(0)|/k

(10)

式(10)为新型趋近律趋近滑模切换面需要的时间。假设两种趋近律的参数相同，即k=k1，将式(6)和不等式(10)比较可知：

(11)

简化后可得：

(12)

由于

|s(0)|/k>0， 0<ε<1

即ε-1<0，故t-t1<0。因此,可得到如下结论：当两种趋近律参数相同，即k=k1时，新型趋近律的趋近速度快于等速趋近律。

另外，当选取的两种趋近律算法的趋紧时间相同时，即t=t1时，可以得到

(13)

由不等式(13)可知，提出的新型趋近律滑模增益要小于等速趋近律滑模增益。因此，新型趋近律和等速趋近律在相同的趋近速度下，相对等速趋近律而言，新型趋近律可以有效减小滑模的抖振问题。

3 并联均流控制策略研究

3.1 下垂法原理

图2给出了2个直流变换器并联的简化系统模型。

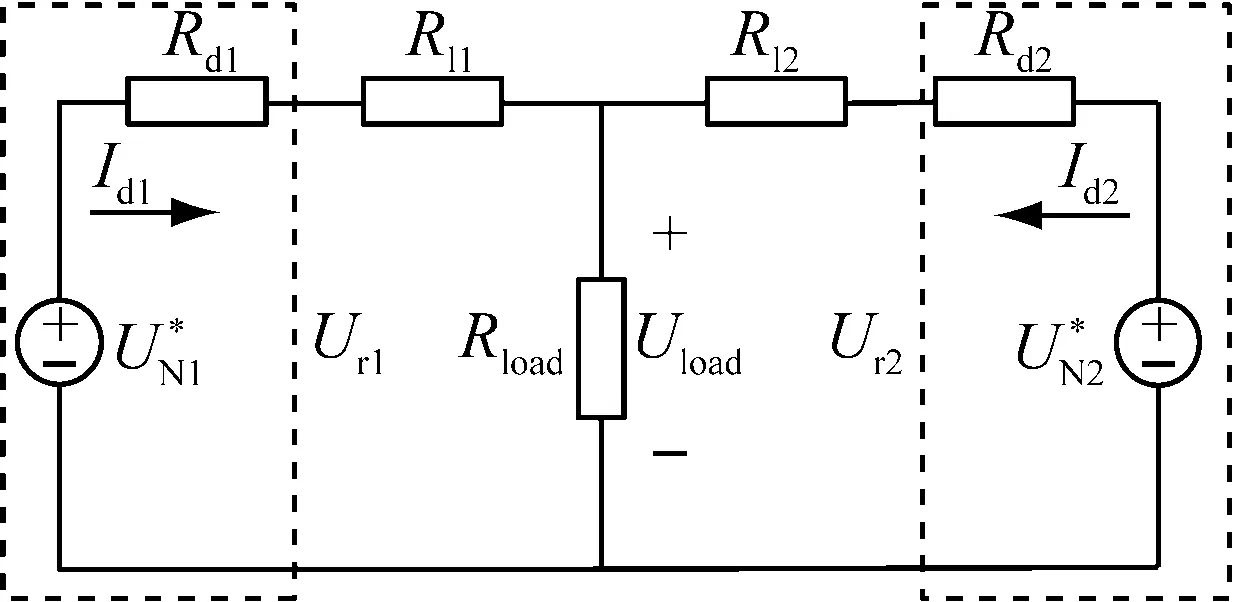
图2 并联系统的简化模型

图中，Ur1、Ur2为变换器的实际输出电压；Id1、Id2为输出电流；Rd1、Rd2为虚拟阻抗；Rl1、Rl2为线路阻抗；Rload为负载；Uload为负载电压。由图可知，每个直流变换器的实际输出电压为

(14)

通过调节变换器的阻抗系数调整变换器的外特性曲线，来实现各个模块的均流。

3.2 直流微电网系统控制策略

下垂原理通过调整输出电压的给定值来实现母线电压的稳定和负荷分配[11]。滑模控制则基于误差(电压给定值和实际电压的误差)和误差的积分作为系统输入，本文将下垂控制得到的值作为滑模控制的误差给定，对直流变换器的并联均流进行控制，图3给出了直流微网的控制框图。

本文采用下垂控制方法的变换器是在滑模控制基础上增加电流反馈环节得到的，因此,下垂控制器参数设计时应先确保滑模控制器的稳定性。为了确保新型趋近律的稳定性，选取Lyapunov函数V=s2/2进行验证。根据Lyapunov稳定性理论可知，当

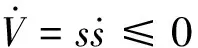
(15)

成立,即可保证新型趋近律稳定性。

由式(7)可得

(16)

式中,eq(x1,s)>0，故

(17)

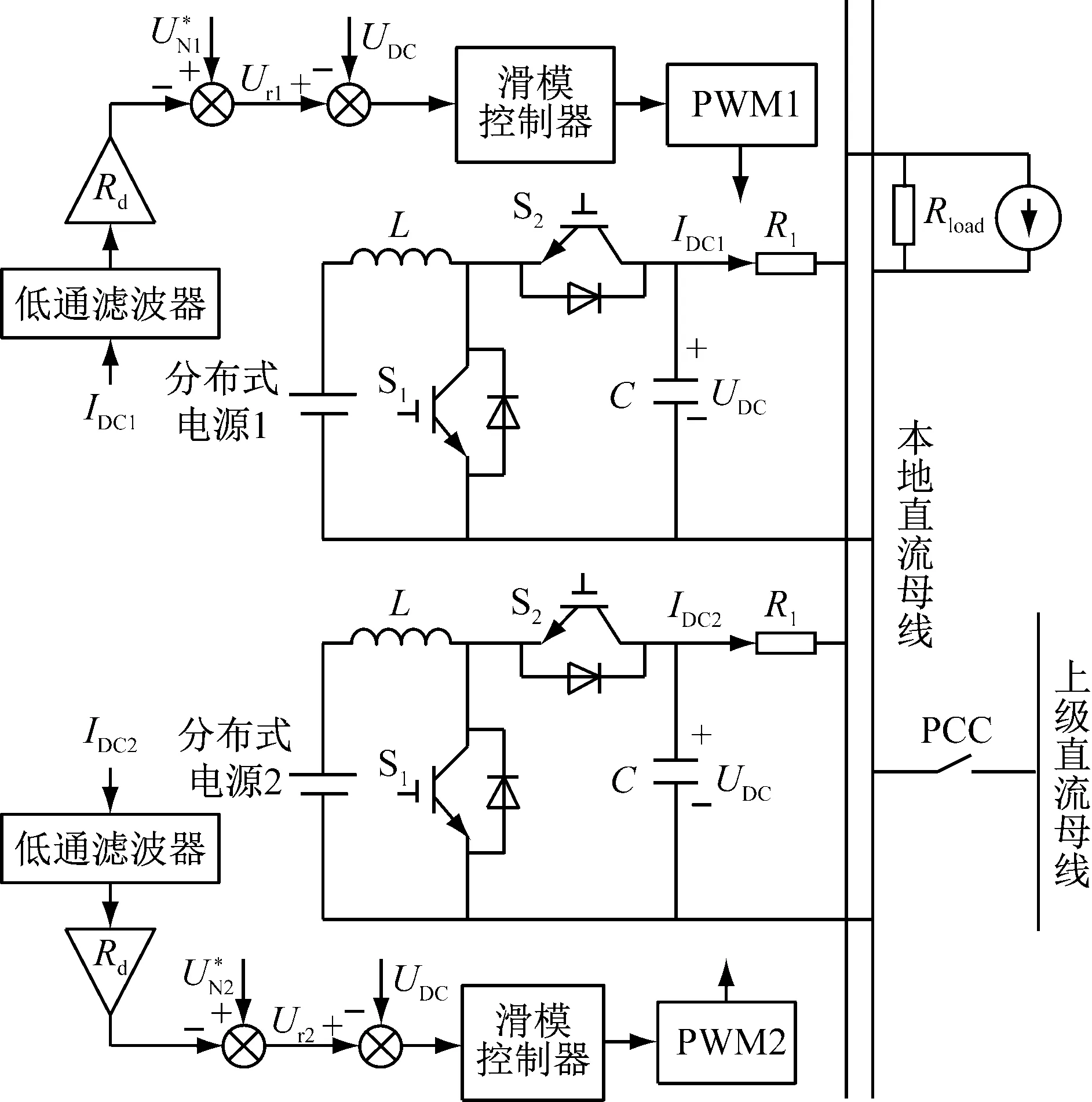
图3 直流微电网控制框图

式(17)表明所提出的新型趋近律可以满足滑模到达条件，能够保证系统稳定性。

4 仿真分析

为了验证算法的有效性，建立了单个直流变换器和2个变换器并联运行的MATLAB仿真模型，仿真部分参数如表1所示。

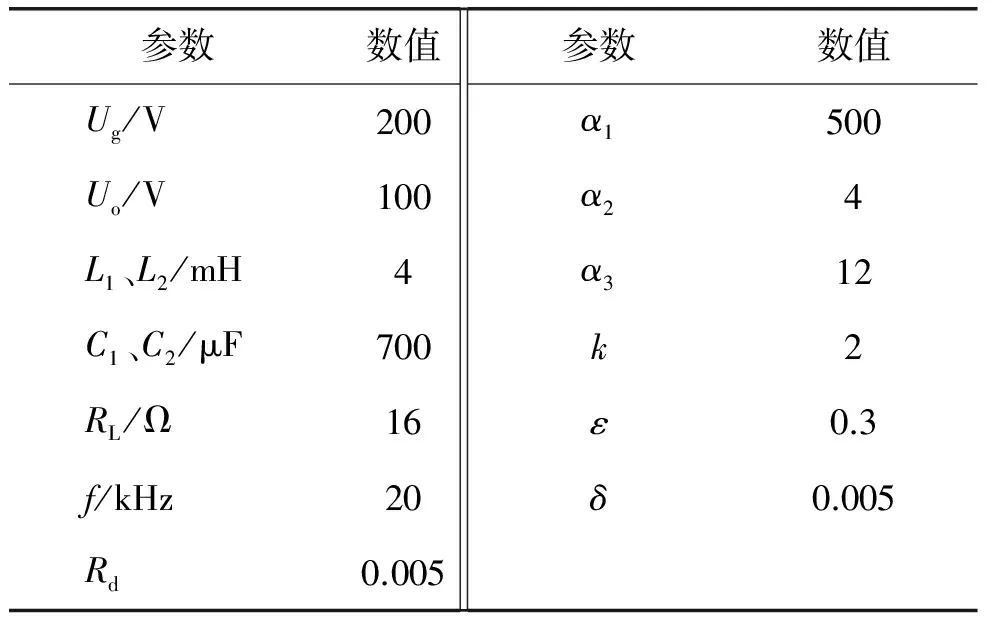
表1 仿真参数

图4给出了直流变换器独立运行时新型趋近律和等速趋近律的输出电压、输出电流。由图可知，新型趋近律在启动时间、负载扰动时的性能都明显优越于等速趋近律，Buck变换器的稳定性、动态性能以及鲁棒性明显提升。

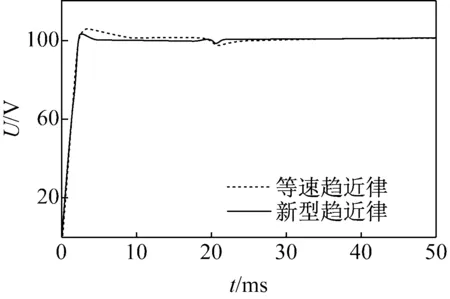
(a) 输出电压

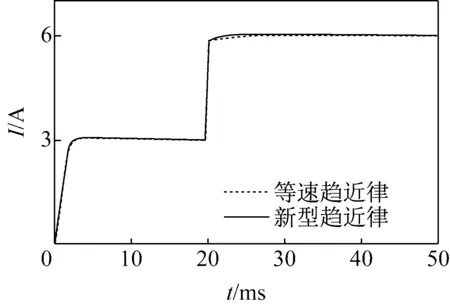
(b) 输出电流

图5给出了直流变换器并联运行时2个Buck变换器的输出电流和直流母线电压。

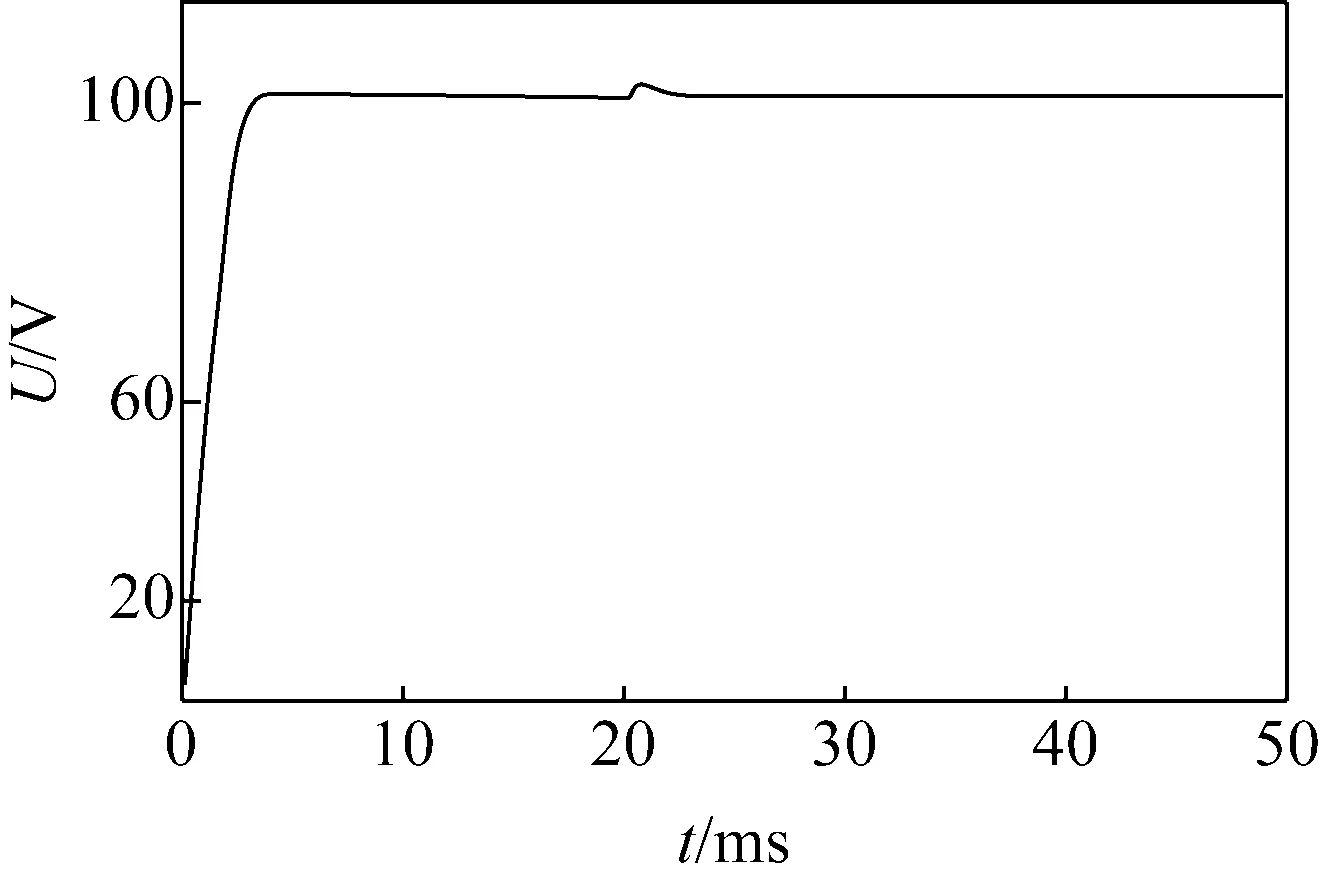
(a) 输出电压

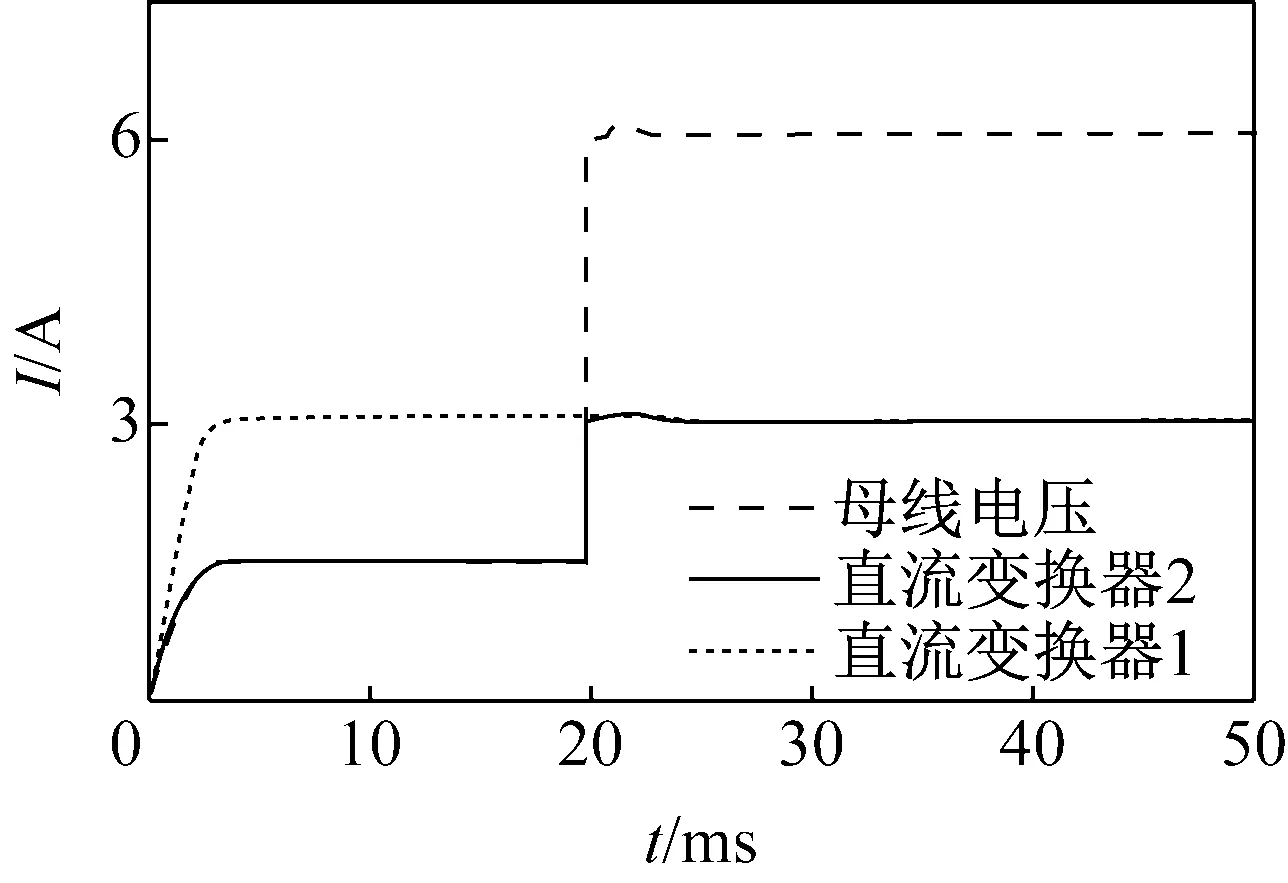
(b) 输出电流

由图5可见,母线电压能够稳定在给定值，且在20 ms负载大幅度变化时,控制策略能够对功率进行快速地重新分配，保证了系统的动态响应速度以及系统的稳定性。

5 结 语

本文对传统等速趋近律趋近时间、抖振问题进行了分析，提出了一种可以有效抑制抖振并且提高系统趋近速度的新型趋近律。利用该趋近律对直流变换器的控制系统进行了设计，同时，结合下垂控制原理，对直流变换器并联运行实验。通过仿真结果可知，本文提出的算法具有良好的稳定性和鲁棒性。

[1] 张学,裴玮,邓卫,等.多源/多负荷直流微电网的能量管理和协调控制方法 [J].中国电机工程学报,2014,34(31): 5553-5562．

[2] 陆晓楠,孙凯,GUERRERO J,等. 适用于交直流混合微电网的直流分层控制系统 [J]. 电工技术学报,2013,28(4): 35-42.

[3] 吕振宇,吴在军,窦晓波. 自治直流微电网分布式经济下垂控制策略 [J]. 中国电机工程学报,2016,36(4): 900-910.

[4] LIU Jinkun, SUN Fuchun. Global sliding mode control with adaptive fuzzy chattering free method for nonlinear system [C]∥IMACS Multi-Conference on Computational Engineering in Systems Applications. Beijing, China: IEEE, 2006:541-546.

[5] GUERRERO J M, HANG L, UCEDA J.Control of distributed uninterruptible power supply systems[J]. EEE Transactions on Industry Electronic, 2008, 55(8):2845-2859.

[6] 解光军,徐慧芳. 峰值电流模式控制非理想 Buck 变换器系统建模 [J].中国电机工程学报, 2012,32(24): 52-58.

[7] 吴宇,皇甫宜耿,张琳,等.大扰动Buck-Boost变换器的鲁棒高阶滑模控制 [J].中国电机工程学报,2015,35(7): 1740-1748.

[8] LING Rui,MAKSIMOVIC D,LEYVA R. Second-order sliding-mode controlled synchronous buck DC-DC converter [J]. IEEE Transactions on Power Electronics, 2015,31(3): 2539-2549.

[9] 张黎,丘水生. 滑模控制逆变器的分析与实验研究[J]. 中国电机工程学报, 2006, 26(3): 59-63．

[10] 支娜,张辉,肖曦.提高直流微电网动态特性的改进下垂控制策略研究 [J].电工技术学报,2016,31(3): 31-39.

[11] 陆晓楠,孙凯,黄立培,等. 直流微电网储能系统中带有母线电压跌落补偿功能的负荷功率动态分配方法 [J].中国电机工程学报,2013,33(16): 37-46.

[12] 帅定新,谢运祥,王晓刚,等. Boost变换器非线性电流控制方法 [J]. 中国电机工程学报,2009,29(15):15-21.

[13] 高为炳. 变结构控制的理论及设计方法 [M]. 北京: 科学出版社, 1996: 241-254.

[13] SHAFIEE Q，GUERRERO J M，VASQUEZ J C．Distributed secondary control for islanded microgrids-a novel approach[J]．IEEE Transactions on Power Electronics，2014，29(2)：1018-1031.

[14] JIN Chi, WANG Peng, XIAO Jianfang, et al. Implementation of hierarchical control in DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8): 4032-4042.

Control of DC Converter in Ship’s Micro-grid Based on a New Approach Law

GULongrui1,CHENJianjun2,ZHANGQinjin1,GUOHaohao1

(1. Marine Engineering College, Dalian Maritime University, Dalian 116026, China; 2. Lianchen Branch of CHALCO, Lanzhou 730000, China)

Control of bus voltage stability and load power allocation is a hot research topic. With constant speed approach controlling, time for approach is long, and chattering is serious in a ship DC converter. To solve the problem, this paper proposes an approaching law aiming to improve the approaching state and make the system performance stable. By combining the theory of power-voltage droop control with a sliding mode controller, a parallel current sharing technique in the DC micro-grid is implemented. Simulation experiments show effectiveness of the proposed method.

ship’s micro-grid; approaching law; DC converter; droop control; robustness

2017 -01 -10

古龙瑞(1990-)，男，硕士生，主要研究方向为船舶直流微电网，E-mail：gulong28@dlmu.edu.cn

2095 - 0020(2017)01 -0022 - 05

U 665.12

A