基于改进滑模观测器的风机降阶系统速度传感器的故障检测

李东亮, 文传博

(上海电机学院 电气学院，上海 201306)

基于改进滑模观测器的风机降阶系统速度传感器的故障检测

李东亮, 文传博

(上海电机学院 电气学院，上海 201306)

针对风力发电机常见的速度传感器故障，建立了传动系统的降阶模型，研究了改进滑模观测器(SMO)的故障检测方法。采用饱和函数削弱抖振对滑模动态的影响，将发电机转速测量差值引入滑模输入信号的设计中，使滑模增益自动调节；同时，利用线性矩阵不等式(LMI)可行性问题设计反馈矩阵。通过对比观测器输出值计算残差估计值，结合最大似然比确定的阈值实现系统故障的有效检测。仿真结果表明所提出的方法能有效检测出风力发电机速度传感器故障。

风力发电机； 滑模观测器； 饱和函数； 线性矩阵不等式； 极大似然比； 故障检测

近年来，随着人们对清洁、可再生能源的需求不断增大，风能在能源市场发挥了重要作用[1]。风力发电机将风能转化为电能，很大程度上满足了人们对清洁能源的需求。与传统能源相比，风力发电成本较高，后期维护投入也较大。因此，开发先进的故障检测和隔离技术，确保风力发电系统可用性，提高可靠性，降低维护成本显得尤为迫切[2-3]。

目前，针对风力发电机系统故障诊断的研究有许多，也提出了一些新技术，包括油分析[4]、应变测量[5]、振动分析[6]等。近年来，基于模型的故障诊断方法得到了广泛关注,文献[7]中提出一种基于未知输入观测器的风力发电机传动和变流器子系统传感器故障检测方法。文献[8]中采用双Kalman滤波器进行传感器故障检测。文献[9]中将Kalman滤波器与观测器相结合，并将其应用于风力发电机故障检测。

由于滑模变结构对模型的不确定性和干扰具有固有的鲁棒性，因此，在故障诊断和其他领域关于滑模观测器(Slide Mode Observer, SMO)的研究较多[10-12]。而采用SMO进行风力发电机故障诊断的研究很少。本文针对风力发电机传动系统常见的转速传感器故障，提出了一种改进SMO的故障检测和隔离方法。在系统故障和不确定性的条件下，所建立的SMO能够估计系统的状态和输出值，通过比较测量值与估计输出值，结合最大似然比阈值的确定，可有效地实现故障的检测。

图1 风力发电机传动系统原理图

1 风机传动系统降阶模型

风力发电机传动系统如图1所示。传动系统中，由速度传感器测量低速轴转速ωr和发电机转子转速ωg，其测量值分别为ωr1、ωr2、ωg1和ωg2。当控制系统速度传感器发生故障时，采用双传感器冗余的方法可实现故障定位与隔离。图中，τg为发电机部分扭矩，τg_ref为发电机转矩参考值。

传动系统模型[13]可表示为

(1)

式中，θΔ为传动系统扭矩角；Br、Bg分别为低速轴和高速轴的黏滞摩擦；Jr和Jg分别为低速轴和高速轴的转动惯性；τr为低速轴扭矩；Kdt为抗扭劲度；Bdt为扭转阻尼系数；Ng为传动比；ηdt为传动系统的效率。

由于传动系统的ωr主要由τr决定，而τr是未知的，估计计算较为困难，考虑到τr仅仅对ωr有直接影响，故可得上述传动系统的降阶模型为

(2)

式中,Ad、B1、B2、Cd、zd均为系数矩阵，即传动系统的模型参数，

ωgm为发电机转速的测量值，本文取平均值，即ωgm=(ωg1+ωg2)/2;发电机转速传感器因故障而产生测量误差Δωg1、Δωg2; Δωgm为转速传感器故障测量误差的平均值，即Δωgm=(Δωg1+Δωg2)/2。

根据式(2)，定义新的状态变量为

则传动系统的降阶模型可进一步表示为

(3)

2 SMO的改进设计

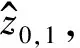
(4)

SMO在滑模变结构输入信号的作用下,将产生一种特殊的滑模运动方式。为了削弱符号函数的不连续特性对系统造成抖振的影响，并消除其带来的高频干扰，本文选用饱和函数作为滑模变结构的输入信号，以降低在滑动模态快速切换时产生的抖振[14-15]，故定义

v1=

(6)

v2=

(7)

定义状态估计误差为

则状态估计误差的动态过程可表示为

定理1 若存在矩阵P0>0，L0满足

(A0-L0C0)TP0+P0(A0-L0C0)<0

(9)

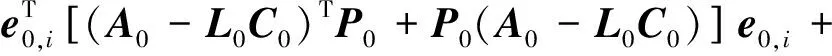
(10)

当且仅当ωr-ωri→0，即低速轴速度传感器无故障时，式(10)可化简为

(11)

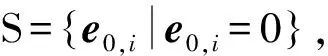
通常,由滑模稳定性条件得出λ>max(Δωg1,Δωg2)，只是指出滑模增益与低速轴转速测量值有关，并没有给出进一步的关系。λ的取值能保证SMO收敛到滑模平面，并决定了收敛速度，一般都取1个正定值;若λ太大，将使状态变量的高频切换作用放大，抖振加剧，并使抖振的噪声增大。本文将λ与2个发电机转子转速传感器的测量差值结合起来，构造如下等式：

(12)

式中，a为实数。

证毕。

引理1[16]假设P0具有对角结构，

(13)

式中，P1和P2均为对称正定矩阵。则式(9)可以转化成线性矩阵不等式(Linear Matrix Inequality, LMI)可行性问题，即存在矩阵P1>0，P2>0，Y>0，满足：

(14)

式中，Y=P2L01。若此LMI是可行的，则可分别通过L01=P2-1Y和F0=P2计算L01、F0。

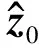
3 故障隔离逻辑

发电机实际转速ωg的估计值为[13]

(15)

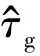
(16)

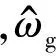
αg、α分别为发电机和变流器模型参数；yc为发电机转矩实际输出值。在风力发电机传动系统中不会受任何其他故障的影响，故可用作隔离方法。设‖，r2=‖‖，r3=‖‖，r4=‖‖，利用最大似然比[17]对上述残差信号进行评估，选定误报率Pf=0.000 5，根据χ2分布表得到判断故障发生的阈值Jth=11.047，因此，故障隔离逻辑策略如表1所示。其中，R1～R4分别为r1～r4的最大似然估计。

4 仿真分析

本文以4.8MW水平轴双馈风力发电机为例[13]，其传动系统相关对应参数如下：Ng=95,ηdt=0.97,Bdt=9.45N·ms/rad,Kdt=2.7 GN·m/rad,Jg=390N·m·s2,Jr=55 MN·m·s2,α=0.1，并依据此风力发电机系统分析选取δ=0.01,a=2。通过建立的SMO及模型参数对其进行仿真分析。当系统发生速度传感器故障时，通过将残差估计值与阈值对比，实现对应故障的诊断。

将上述参数代入式(3)，得

考虑到传动系统常见传感器故障，在系统仿真中使用表2所示的故障信号。

表2 仿真故障信号

(a) 普通SMO

(b) 改进SMO

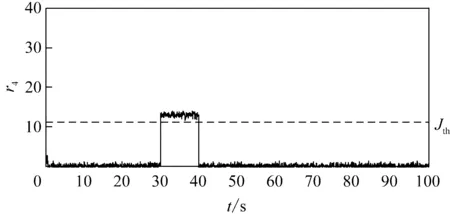
当转速传感器在40～50s出现故障F1、在30s～40s出现故障F2和F3时，仿真结果如3、4所示。

由图3、4可见，在30～40s时间段，r2和r4估计明显偏离零点，且大于阈值Jth，而r1和r3保持在零点附近，由表1所示决策逻辑可得到如下结论： 在30～40s内，低速轴速度传感器2和发电机速度传感器2发生故障；同理，在40～50s内，r1估计明显偏离零点，且大于阈值Jth，低速轴速度传感器1发生故障。

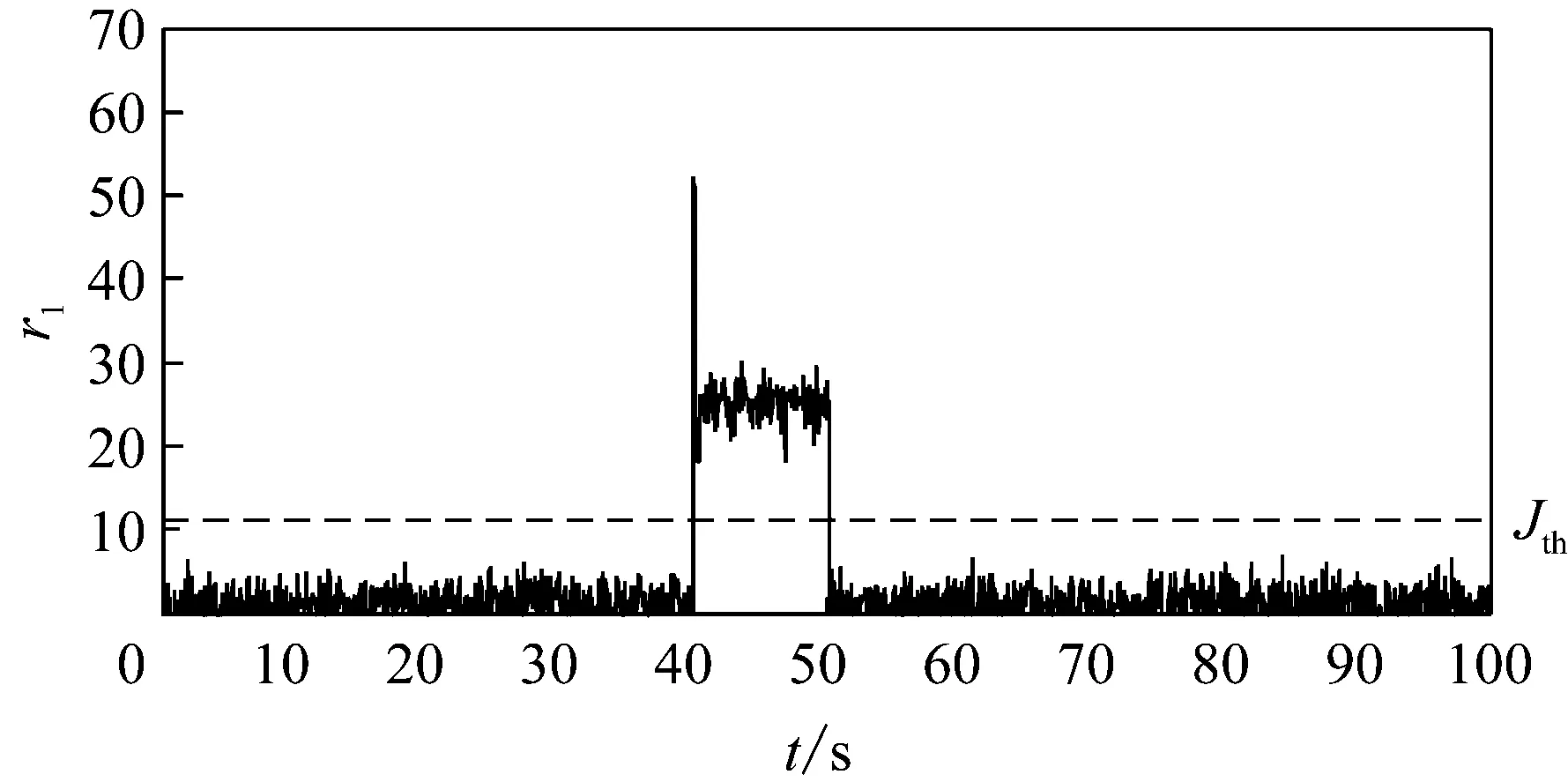
(a)r1估计与阈值对比

(b) r2估计与阈值对比

(a) r1估计与阈值对比

(b) r2估计与阈值对比

5 结 语

本文在风力发电机传动系统模型的基础上提出的降阶模型，降低了系统复杂的程度。在进行SMO设计时，采用饱和函数削弱系统抖振，利用发电机转子转速测量差值设计滑模增益，将反馈矩阵的配置问题转化为LMI求解问题，并结合最大似然比估计残差确定了阈值，仿真结果证明基于改进SMO的降阶模型方法能有效地检测出风力发电机速度传感器故障。

[1] 宋恒东,董学育.风力发电技术现状及发展趋势 [J].电工电气,2015(1)： 1-4.

[2] 刘吉臻,王海东,李明扬.含风电的电力系统机组组合问题研究综述 [J].电力建设,2014,35(12)： 38-45.

[3] SUN Shengpeng, LIU Fengliang, XUE Song, et al. Review on wind power development in China： Current situation and improvement strategies to realize future development [J]. Renewable & Sustainable Energy Reviews,2015,45： 589-599.

[4] 徐明辉,李泽滔,陶金. 三相对称故障下双馈风力发电机控制策略 [J].电力建设,2014,35(8)： 130-133.

[5] HAMEED Z,HONG Y S,CHO Y M,et al.Condition monitoring and fault detection of wind turbines and related algorithms： A review [J]. Renewable and Sustainable Energy Reviews,2009,13(1)： 1-39.

[6] LU Bin,LI Yaoyu,WU Xin,et al.A review of recent advances in wind turbine condition monitoring and fault diagnosis [C]∥Proceedings of IEEE Power Electronics and Machines in Wind Aplications.[S.l.]:IEEE,2009:1-7.

[7] ODGAARD P F, STOUSLRUP J, NIELSEN R,et al.Observer based detection of sensor faults in wind turbines [EB/OL].[2016-01-20].http：∥proceedings.ewea.org/ewec2009/allfilesz/34_EWEC2009_presentation.pdf.

[8] WEI Xiukun,VERHAEGEN M,van ENGELEN T.Sensor fault detection and isolation for wind turbines based on subspace identification and Kalman filter techniques [J]. International Journal of Adaptive Control and Signal Processing,2010,24(8)： 687-707.

[9] CHEN Wei,DING S X,HAGHANI A S,et al.Observer-based FDI schemes for wind turbine benchmark [C]∥Proceedings of the 18th IFAC World Congress.Milano, Italy： IFAC, 2011： 7073-7078.

[10] EDWARDS C,SPURGEON S K,PATTON R J.Sliding mode observers for fault detection and isolation [J].Automatica, 2000,36(4)： 541-553.

[11] YAN Xinggang,EDWARDS C.Nonlinear robust fault reconstruction and estimation using a sliding mode observer [J].Automatica,2007,43(9)： 1605-1614.

[12] ZHANG J,SWAIN A K,NGUANG S K.Detection and isolation of incipient sensor faults for a class of uncertain non-linear systems [J]. IET Control Theory & Applications,2012,6(12)： 1870-1880.

[13] ODGAARD P F, STOUSTRUP J, KINNAERT M. Fault-tolerant control of wind turbines： A benchmark model [J]. IEEE Transactions on Control Systems Technology,2013,21(4)： 1168-1182.

[14] 朱明东,黄科元,黄守道,等.基于新型滑模观测器的永磁直驱风机控制 [J].电源技术,2016,40(3)： 672-674，679.

[15] ZHANG Jian,BENNOUNA O,SWAIN A K,et al,Detection and isolation of sensor faults of wind turbines using sliding mode observers [C]∥2013 International Renewable and Sustainable Energy Conference.Ouarzazate, Morocco： IEEE,2013： 234-239.

[16] 高金凤,俞立,王春平.线性矩阵不等式及其在控制工程中的应用 [J].控制工程,2003,10(2)： 145-148，189.

[17] 赵军圣,庄光明,王增桂.极大似然估计方法介绍 [J].长春理工大学学报(自然科学版),2010，5(6)： 53-54.

Detection of Speed Sensor Faults of Reduced System in a Wind Turbine Using Sliding Mode Observer

LIDongliang，WENChuanbo

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)

To detect speed sensor faults in a wind turbine, this paper establishes a reduced order model of the drive system, and proposes an improved fault detection method with a sliding mode observer (SMO). The SMO design takes advantages of saturation function to weaken the influence of chattering of sliding mode dynamic, and introduces wind rotor speed difference to realize automatic gain adjustment. Feedback matrix is designed based on the linear matrix inequality (LMI) feasibility problem. By comparing the output value of the observer and the estimated value, the threshold value of maximum likelihood ratio is determined to detect the system failure. Simulation results show that the proposed method can detect faults in a wind turbine speed sensor effectively.

wind turbine; sliding mode observer (SMO); saturation function; linear matrix inequality (LMI); maximum likelihood ratio; fault detection

2016 -10 -24

李东亮(1992-)，男，硕士生，主要研究方向为风力发电机故障诊断，E-mail： 1278451173@qq.com

指导老师： 文传博(1981-)，男，讲师，博士，主要研究方向为风电机组故障诊断、目标跟踪与状态估计、多源信息融合， E-mail： chuanbowen@163.com

2095 - 0020(2017)01 -0016 - 06

TM 614; TP 277.3

A