基于多重分形维数的改进信号特征提取算法

李靖超， 陈志敏

(上海电机学院 电子信息学院，上海 201306)

基于多重分形维数的改进信号特征提取算法

李靖超， 陈志敏

(上海电机学院 电子信息学院，上海 201306)

针对复杂环境下，辐射源个体细微特征难于提取的问题，提出了一种改进多重分形维数辐射源个体特征提取算法。该算法对传统的多重分形维数算法进行了简化，取消了对传统多维特征进行求和的步骤，所得到的新的多重分形维数特征，对于辐射源个体特征的提取更具有针对性。仿真结果表明，提取到的多重分形维数特征可以较好地刻画辐射源个体特征，进而为后续分类器的设计打下良好的基础。

信号识别； 多重分形维数； 特征提取

早期的辐射源个体识别(Specific Emitter Identification, SEI)[1-3]针对的大多是雷达辐射源信号。近年来，通信电台个体特征分析逐渐成为电子战研究领域的一个热门课题。这种电台的细微特征个体识别属于非协作通信范畴，在接收方不具有发射信号的任何信息或只具有少量信息的情况下，利用专业的电子侦查装备对辐射源发出的无线电信号进行搜索、截获、识别、定位和分析。由于通信信号相对于雷达信号其技术参数差异较小，因而研究难度相对更大。

随着电子器件的工艺水平不断提高，同型电台之间的细微差异逐渐减小；在恶劣的通信环境下，信号的这种细微特征很容易被噪声湮没，对其特征的检测与提取成为很多人关注的问题。传统的辐射源个体识别算法已经得到了比较广泛的应用。基于高阶累积量[4-6]特征参数对信号星座图的平移、尺度和相位旋转具有不变性，在个体信号识别中已得到较好的应用，但是，在数据长度有限和噪声不平稳的情况下，将难以区分待识别个体信号。基于信号功率谱[7-8]和高次方谱[9-10]的特征参数，较时域统计参量[11-13]具有更好的抗噪声性能，但是，信号的非线性变换会破坏特征的有效性，使提取特征的可分离度降低。

分形维数[14-16]是分形理论中的重要参数, 它有多种定义和计算方法, 常用的有Hausdorff维数[17]、盒维数[18]、信息维数[19]、相似维数[20]、关联维数[21]和广义维数[22]等。Hausdorff 维数是分形理论中一种最基本的分形维数, 但在实际应用中, Hausdorff 维数的计算较困难,因此，采用盒维数描述分形信号的几何尺度信息，采用信息维数描述分形信号在平面空间上的分布信息；而多重分形维数[23]可以从更精细的角度刻画辐射源信号不同层次的信息。本文提出了基于多重分形维数的通信信号识别算法，并对多重分形维数进行了改进。仿真结果表明，改进算法具有更好的规律性与可测性。

1 改进多重分形维数算法

Mandelbrot在1975年提出了分形理论，建立了一种描述自然界复杂性的新的科学方法[24]。近几年来，分形维数受到了广泛关注，已成功地应用到自然科学和社会科学的许多领域，为描述客观世界提供了一个新工具。分形是由一些与其整体以某种方式相似的部分所组成的形体, 它具有精细结构和在近似或统计意义下的某种自相似性。分形维数可以度量信号波形的复杂度和不规则性, 因此，把通信信号作为一种时间序列, 可用分形维数来对其进行刻画。

分形维数是度量信号不规则性、探索事物复杂度的重要指标，目前，已在图像分析、振动信号故障诊断、动力学分析中得到了广泛应用。对于简单信号，一维分形维数——盒维数就可以描述其特征；而对于复杂信号，则需要用多个分形参量来描述不同层次的局域特征。为了进一步了解信号的局部分形特性，提取其不同层次的复杂度特征，引入了多重分形的概念；多重分形理论的提出，使对电台辐射源细微特征的提取成为可能。

在多重分形维数的定义中，把研究对象(取其线度为1)分为N个小区域，设第i个区域的线度大小为εi，则第i个区域的密度分布函数Pi用不同的标度指数αi描述为[23]

(1)

式中，αi为非整数，一般称为奇异指数。

定义函数Xq(ε)为各个区域的概率加权求和[23]，即

(2)

式中，q为各个区域的概率加权指数。

由此进一步定义广义分形维数为[23]

(3)

从多重分形维数的定义中可见，在对信号的各个区域进行分形维数刻画时，采用的是累加的方式进行总体特征求和；这种求和方式累积了各个区域的信号特征。由于要提取的是辐射源个体的细微特征，而细微特征的存在只是在辐射源个体信号的一部分时间段中才出现，因此，累加的过程反而弱化了细微特征的存在。针对这个特点，本文提出了基于多重分形维数的辐射源个体局部特征提取算法，提取辐射源信号各个部分的细微特征，保留各个相加项，取消累加的过程，进而达到对局部细微特征进行识别的目的。

算法的改进中，取消了对函数Xq(ε)的计算，直接计算各个局部特征的分形维数，即定义

(4)

这样，既简化了算法，又更为精确地捕捉辐射源电台的细微特征变化，从而达到更精确识别电台的目的。

2 仿真结果与分析

根据理论分析，多重分形维数可以描述信号的多重复杂度特征，因此，以幅度调制信号(AM)为例，信号幅度A=1，载波频率fz=0.27 GHz，采样频率fs=4.32 GHz，基带信号频率fm=100 kHz，调制指数a=0.8，利用式(4)求取信号的多重分形维数特征，探讨信号的多重分形维数特征的特性。本文在MATLAB平台上，得到AM调制信号的多重分形曲线如图1所示。

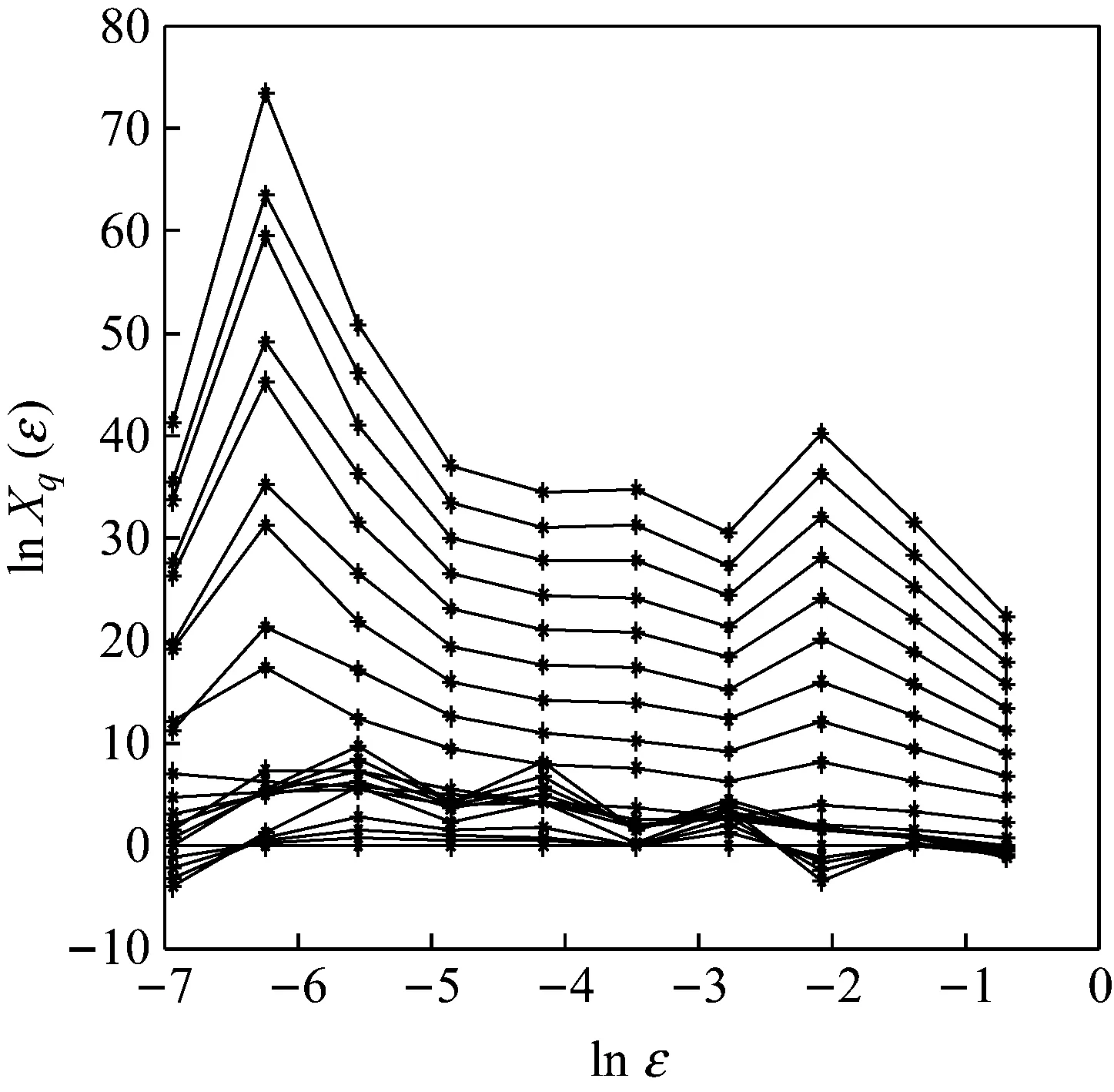
图1 AM调制信号的多重分形曲线图

图中，10个lnε值对应了21条q值(-10≤q≤10)曲线。由图1可见，重构相空间的数目对最终的多重分形结果会产生影响，每组相空间元素的个数太多时(对应图中右侧曲线)或太少时(对应图中左侧曲线)，得到的最终分形曲线并不稳定，只有当lnε-1在-5～-3时多重分形曲线才比较稳定，因此，相空间重构的维数选在23～25较为合适，可以达到更好的特征提取效果。

以2种不同的色噪声(高斯色噪声和粉红噪声)为例，其中，高斯色噪声均值E1=0.2，方差σ1=0.7，粉红色噪声均值E2=0.9，方差σ2=3.2。图2给出了2种不同分布色噪声的随机序列图。由图可见，2种噪声存在着细微分布的不同，可近似地认为，将该噪声同时附加在相同电台发射信号上的微小噪声也不同。

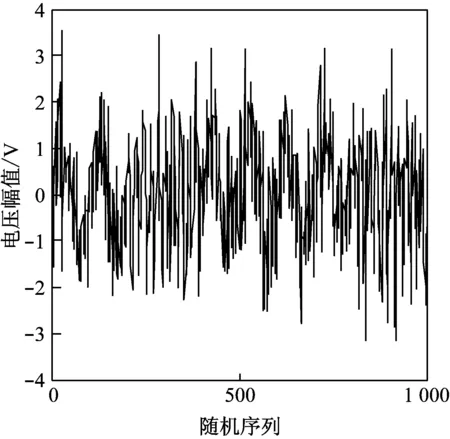
(a) 高斯色噪声

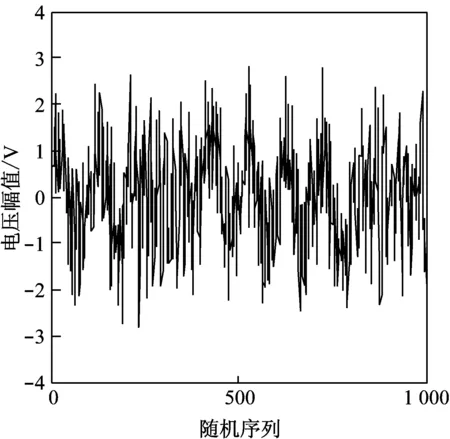
(b) 粉红色噪声

为验证多重分形维数对电台的识别效果，分别将上述2种信号附加在频移键控(Frequency-Shift Keying，FSK)信号上进行噪声识别，特征提取结果如图3所示。

由图3的仿真结果可见，附加不同分布噪声的FSK信号具有不同的分形维数特征，如果选择合理的分类器，可以达到对辐射源个体进行识别的目的。利用文献[25]中提出灰色关联分类器算法对提取到的特征结果进行验证，在上述仿真条件下，可以达到100%的识别率。

利用改进的多重分形维数算法对模拟的2种电台内部噪声进行特征提取，提取到的多重分形维数特征如图4所示。

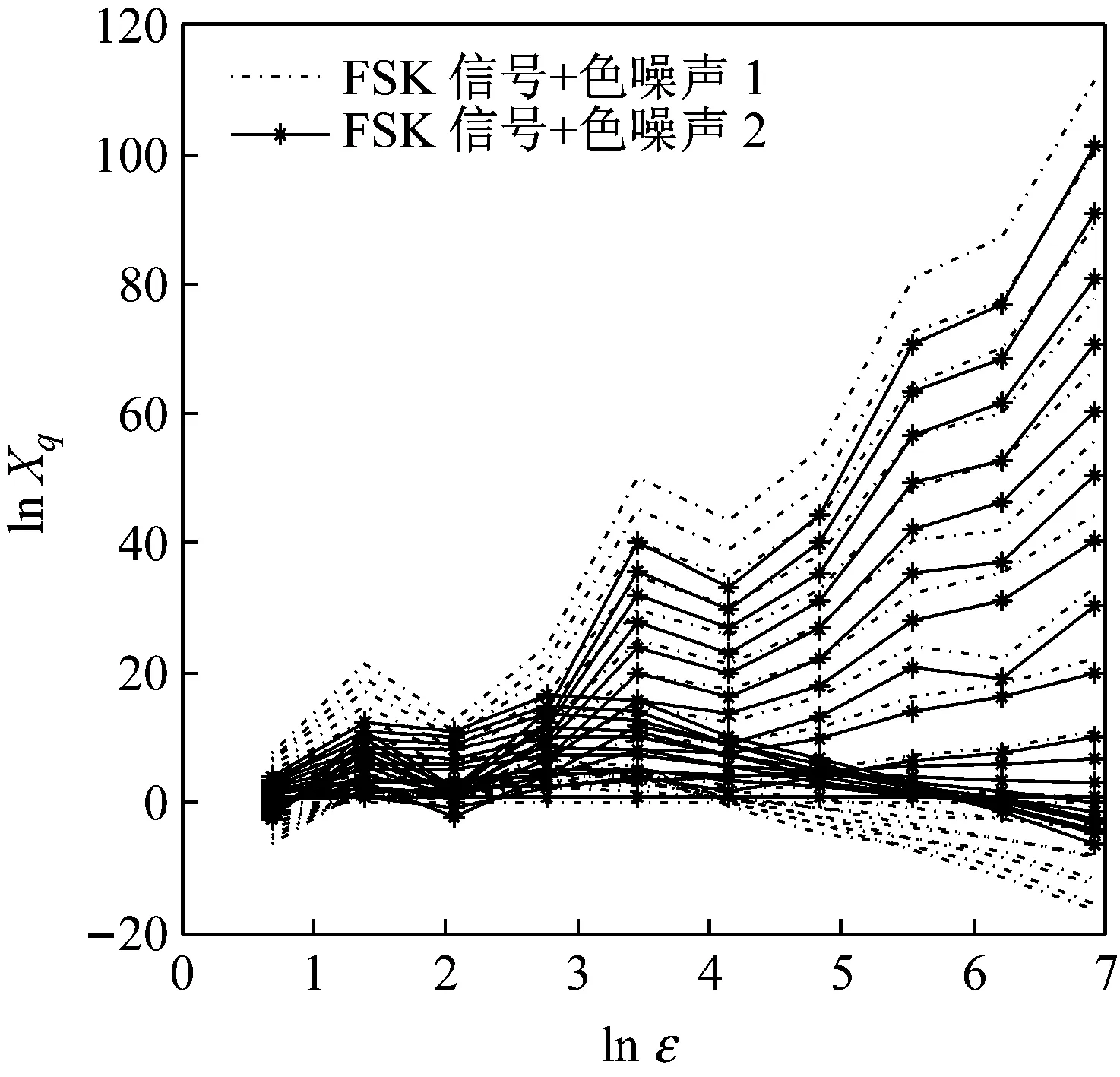
图3 附加不同分布色噪声的FSK信号的多重分形维数特征

图4 附加不同分布色噪声的FSK信号的改进多重分形维数特征

Fig.4 Improved multi-fractal dimension characteristics of FSK signals with noise of different color spectra

由图4可见，附加不同分布色噪声的FSK信号的改进多重分形维数特征具有更好的规律性和可分离度。由于提取到的多重分形维数的每一维特征代表的并不是信号的整体特征，而是代表信号的每一部分的细微特征，这样，对有细微变化的电台信号具有更好的特征提取效果，因此，分离度相应增大，为后续的分类器设计做了更好的铺垫。同理，利用文献[25]中提出的灰色关联分类器算法对提取到的特征结果进行验证，在上述仿真条件下，仍可以达到100%的识别率。

3 结 语

目前，分形维数的研究主要表现在对信号的仿真建模广泛地应用到多个领域。本文针对基于多重分形维数的通信辐射源个体特征提取算法，在MATLAB平台上，以色噪声模拟电台内部细微噪声，并根据辐射源个体识别的特点，对多重分形维数算法进行了改进，取消了多重分形传统算法中的多维特征求和的累加过程，进行了简化计算，得到的多重分形维数值是信号的某一维特征的刻画。该改进算法在简化传统算法的同时，使提取的特征更具有针对性。仿真结果表明，改进的多重分形维数算法计算相对简单，且对辐射源个体识别具有更好的规律性和可控性，具有更大的应用价值。

[1] 史亚, 姬红兵, 朱明哲, 等. 多核融合框架下的雷达辐射源个体识别 [J]. 电子与信息学报, 2014, 36(10): 2484-2490.

[2] JIANG Haiqing， GUAN Wenshuo, AI Lan. Specific radar emitter identification based on a digital channelized receiver[C]// 2012 5th International Congress on Image and Signal Processing (CISP). Chongqing: IEEE, 2012:1855-1860.

[3] 蔡忠伟, 李建东. 基于双谱的通信辐射源个体识别 [J]. 通信学报, 2007, 28(2): 75-79.

[4] LI Peihua, ZHANG Hongxin, WANG Xuying, et al. Modulation recognition of communication signals based on high order cumulants and support vector machine [J]. Journal of China Universities of Posts and Telecommunications, 2012,19(1): 61-65.

[5] HAO Siyuan, WANG Wei, YAN Yan, et al. Class-wise dictionary learning for hyperspectral image classification [J]. Neurocomputing,2017, 220:121-129.

[6] 陆凤波, 黄知涛, 易辉荣, 等. 一种基于高阶累积量的数字调相信号识别方法 [J]. 系统工程与电子技术, 2008, 30(9): 1611-1615.

[7] LI Jingchao. A new robust signal recognition approach based on holder cloud features under varying SNR environment [J]. KSII Transactions on Internet and Information Systems, 2015, 9(12):4934-4949.

[8] YING Yulong, CAO Yunpeng, LI Shuying, et al. Study on gas turbine engine fault diagnostic approach with a hybrid of gray relation theory and gas-path analysis [J]. Advances in Mechanical Engineering, 2016,8(1):1-14.

[9] BIANCHI A M, MAINARDI L, PETRUCCI E, et al. Time-variant power spectrum analysis for the detection of transient episodes in HRV signal [J]. IEEE Transactions on Biomedical Engineering, 1993,40(2):136-144.

[10] WOESTE L. Femtosecond white-light filaments: A new tool in atmospheric research[C]// The 17th Annual Meeting of the IEEE Lasers and Electro-Optics Society. [S.l.]: IEEE, 2004:623-624.

[11] 朱雷, 程汉文, 吴乐南. 利用循环谱和参数统计的数字调制信号识别 [J]. 应用科学学报, 2009, 27(2): 137-143.

[12] 吴月娴, 葛临东, 许志勇. 常用数字调制信号识别的一种新方法 [J]. 电子学报, 2007, 35(4): 782-785.

[13] KIM C , KHAWAND C, STERN R M. Two-microphone source separation algorithm based on statistical modeling of angle distributions[C]// 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Kyoto, Japan: IEEE, 2012:4629-4632.

[14] 叶菲, 罗景青, 海磊. 基于分形维数的雷达信号脉内调制方式识别 [J]. 计算机工程与应用, 2008, 44(15): 155-157.

[15] 李兵, 张培林, 米双山, 等. 齿轮故障信号多重分形维数的形态学计算方法 [J]. 振动、测试与诊断, 2011, 31(4): 450-453.

[16] Di MARTINO G, IODICE A, RICCIO D, et al. Angle independence properties of fractal dimension maps estimated from SAR data [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013,6(3):1242-1253.

[17] 王冰, 李洪儒, 许葆华. 基于数学形态学分段分形维数的电机滚动轴承故障模式识别 [J]. 振动与冲击, 2013, 32(19): 28-31,92.

[18] LIU Xiaobo, SHEN Liangni. Fault diagnosis in cracked rotor based on fractal box counting dimension [C]// 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering (CMCE). [S.l.]: IEEE, 2010 : 356-360.

[19] 吕铁军, 郭双冰, 肖先赐. 调制信号的分形特征研究 [J]. 中国科学 E辑: 技术科学, 2001, 31(6): 508-513.

[20] ANKERST M, BERCHTOLD S, KEIM D A. Similarity clustering of dimensions for an enhanced visualization of multidimensional data [C]// IEEE Symposium on Information Visualization. [S.l.]: IEEE, 1998:52-60,153.

[21] 姬翠翠, 朱华, 江炜. 混沌时间序列关联维数计算中无标度区间识别的新方法 [J]. 科学通报, 2010，55(31): 3069-3076.

[22] 徐玉秀, 钟建军, 闻邦椿. 旋转机械动态特性的分形特征及故障诊断 [J]. 机械工程学报, 2005, 41(12): 186-189.

[23] CHAKRABORTY B, HARIS K, LATHA G, et al. Multifractal approach for seafloor characterization [J]. IEEE Geoscience and Remote Sensing Letters, 2014,11(1):54-58.

[24] 孙洪军,赵丽红. 分形理论的产生及其应用 [J]. 辽宁工学院学报, 2005, 25(2):113-117.

[25] LI Yibing, LI Jingchao, KANG Jian. Classifier design algorithms aimed at overlapping characteristics [J]. Information Technology Journal, 2012, 11(8): 1091-1096.

Signal Feature Extraction Based on Improved Multi-fractal Dimension

LIJingchao,CHENZhimin

(School of Electronic Information, Shanghai Dianji University, Shanghai 201306, China)

As subtle characteristics of radiation sources are difficult to extract in a complex environment, a feature extraction algorithm based on improved multi-fractal dimension is proposed. Compared with traditional multi-fractal dimension algorithms, the steps for summing up multi-dimensional features are eliminated for simplification and for being specific to characteristics extraction from individual signals. Simulation results show that the extracted multi-fractal dimension features can well characterize the radiation source, and therefore lay a good foundation for the subsequent design of classifiers.

signal recognition; multi-fractal dimension; feature extraction

2017 -01 -25

国家自然科学基金青年基金项目资助(61603239，61601281)

李靖超(1986-)，女，讲师，博士，主要研究方向为信号处理、辐射源识别，E-mail：lijc@sdju.edu.cn

2095 - 0020(2017)01 -0006 - 05

TN 911.72

A