模糊综合评价法在水资源承载力中的应用
2017-04-13周丽
周 丽
(温州大学数学与信息学院,浙江 温州 325035)
模糊综合评价法在水资源承载力中的应用
周 丽
(温州大学数学与信息学院,浙江 温州 325035)
在简述模糊综合评价法的基础上,选取了9个评价指标和3个分级指标,建立了水资源承载力的模糊综合评价模型。以温州市为例,运用模糊综合评价法,对温州市2007 — 2011年的水资源承载力进行综合评价。结果表明,温州市水资源承载力状况良好,都是适载或轻载,无超载现象;年降水量指标对水资源承载力的评价结果影响较大。最后提出若干措施和建议。
水资源承载力;模糊综合评价;温州市
水资源承载力是水资源领域中的承载力概念,始于1989年新疆水资源软科学课题组对新疆的水资源承载力和开发战略对策进行研究[1]。目前水资源承载力没有统一定义,典型代表如夏军等认为水资源承载力是指在一定的水资源开发利用阶段,满足生态需求的可利用水量能够维系有限发展目标的最大的社会—经济规模[2]。水资源承载力是可持续发展研究和水资源安全战略研究中的一项基础课题,也是当前水资源科学研究中的热点问题。水资源承载力研究方法主要有常规趋势法、模糊评价分析法、系统动力学方法、多目标决策分析法、主成分分析法等[3-6]。由于水资源具有不确定性和模糊性,故用模糊综合评价法能够较好地对水资源承载力进行多因素综合评定,全面地反映区域水资源承载力状况。张晓鹏[7]等(2009年)基于模糊综合评价法对区域水资源承载力进行研究,并对榆林市水资源承载力展开了综合评价;董小曼[8]等(2010年)运用模糊综合评价法对山东省聊城市的水资源承载力做出了评价。目前以温州市作为研究对象的水资源承载力的研究尚属空白,进行温州市水资源承载力模糊综合评价研究具有现实意义。
1 模型方法
1.1 模糊综合评价法简介
1965年,美国加州大学的控制论专家扎德发表了1篇题为《Fuzzy Sets》的论文,标志着模糊数学诞生。模糊数学将数学的应用范围从精确现象扩大到模糊现象。对于一个具有多个模糊性特征的事物,在进行评价时需借助于模糊数学的处理方法,以做出合理的评价。模糊综合评价法是以模糊数学为基础,应用模糊关系合成的原理,将一些边界不清或定性的因素定量化,从多个因素对被评价事物隶属等级状况进行综合性评价的一种方法。
模糊综合评价法的建模步骤:
(1)确定评价因素集。对于评价对象,首先需要明确表征该对象的因素有哪些,根据评价的目的,筛选出反映评价对象的主要因素,用相应指标进行度量,形成评价因素集。设反映被评价对象的主要因素有m个,分别用u1、u2、…、um表示,则有评价因素集记为U = {u1、u2、…、um}。
(2)确定评价等级集。对于每个因素,可以确定若干个等级。如果划分的等级有n个,分别用ν1、ν2、…、νn表示,则有评价因素集记为V ={ν1、ν2、…、νn}。
(3)建立评价矩阵。对于评价因素集中的每个因素ui(i = 1,2,…,m),分析其对于评价等级νj(j = 1,2,…,n)的隶属度rij,得出第i个因素的单因素评价结果ri= (ri1、ri2、…、rin)。将ri作为第i行,形成一个综合了m个因素n个评价等级的模糊评价矩阵R:

(4)确定权重向量。权重向量是衡量各评价因素对被评价对象的贡献程度的,分为主观赋权法和客观赋权法。如果评价因素ui的权重为wi,则相应于因素集U的权重向量可以表示为W={w1、w2、…、wm},要求wi≥0,且 Σwi=1。
(5)模糊合成。在模糊评判矩阵R和权重向量W已经确定的基础上,用权重向量W对矩阵R进行模糊运算,即可得到从总体上看被评价对象对各评价等级的隶属程度,即为模糊综合评价的结果向量B ={b1、b2、…、bn},要求i=1。用模糊算子表示为:

式中:o为模糊算子符号。算子符号不同,相应的模糊综合评价模型亦不同,常用的算子有Zadeh算子、加权平均算子、取大乘积算子等。
(6)做出决策。 模糊综合评价结果向量B ={b1、b2、…、bn},bj表示被评价对象隶属于评价等级νj的程,其中最大的bj对应的等级νj表示评价对象最适合于该等级,可以用该等级作为被评价对象的评价结果,即按照最大隶属度原
这里要求则做出决策。
1.2 水资源承载力的模糊综合评价模型
1.2.1 指标体系的建立
影响水资源承载力最主要的因素涉及经济、社会、环境等。按照科学性、代表性、可行性的选取原则,并参照全国水资源供需平衡分析中的指标体系,选取了以下10个指标构成评价体系:
(1)水资源方面:u1年降水量(mm),u2水资源利用率(75%保证率的供水量与可利用的水资源总量之比,%),u3人均拥有水资源量(75%保证率可供水资源量与总人口数之比,m3);
(2)生态方面:u4有效灌溉面积(khm2),u5环境用水率(用生态环境用水量占总用水量比例表示,%);
(3)社会经济方面:u6城市化水平(用非农人口占总人口比例表示,%),u7万元工业增加值用水量(m3),u8人均GDP(万元),u9居民生活人均日用水量(m3)。
1.2.2 分级指标的建立
按照上述9个评价因素对区域水资源承载力的影响程度,将其划分为V1、V2和V3三个等级,每个因素各等级的数量指标见表1。 等级V1级代表水资源承载力是轻载的,水资源利用情况良好,意味着该地区的水资源还有一个较大的承载能力。等级V3表示水资源承载力是超载的,水资源状况较差,水资源承载力已到达一定极限,进一步开发利用潜力不大,强行开发会导致生态环境恶化。等级V2的情况是介于以上两者之间,水资源承载力是适载,意味着该地区水资源开发利用已有相当规模,但是还有一定的开发利用潜力。为了更好地反映水资源承载力的每一类情况,给V1、V2和V3这3个等级进行0 ~ 1之间评分,a1= 0.95,a2= 0.50,a3= 0.05,分值越高,表明水资源开发潜力越大。

表1 各评判因素分级值表
1.2.3 评判矩阵的建立
评判矩阵R中rij可以通过评价因素的实际数值对照各因素的分级指标来计算。为了使隶属函数可以在各等级之间平滑过渡,需对其进行模糊化处理。V2级是中间范围,所以令其落在中间点的隶属度为1.0,两侧边缘点的隶属度为0.5,中点向两侧按线性递减处理。对于V1、V3两侧区间,使其距临界值越远属两侧区间的隶属度越大,在临界值上则属于两侧等级的隶属度各位0.5。记V1和V2级的临界值为k1,V2和V3级的临界值为k3,V2等级区间中点值为k2,k2= (k1+ k3) / 2。负向指标(如评价因素u2、u4、u6、u7、u9)的隶属函数公式如下:
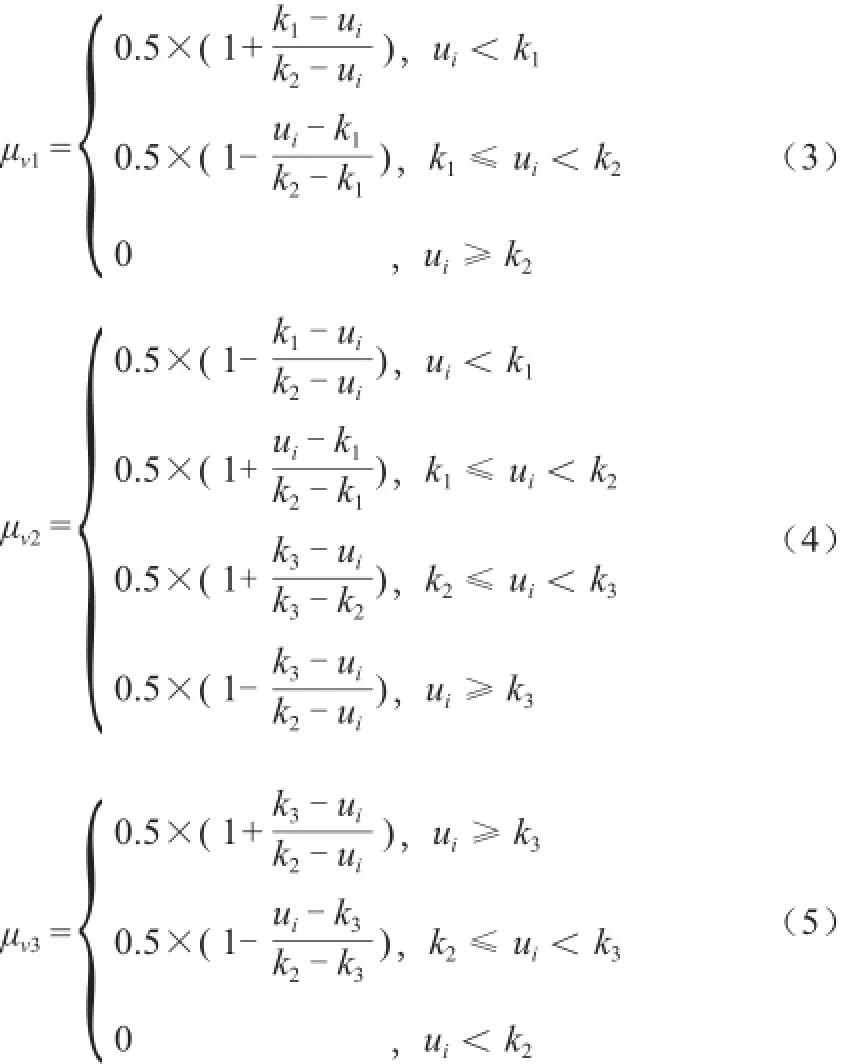
正向指标(如评判因素u1、u3、u5、u8)的相对隶属函数公式只需将上述公式的右边ui区间号“≥”改为“≤”以及“<”改为“>”,本文就不再详细列出。判断矩阵R的第i行的第1列、第2列和第3列元素对应为ri1= μν1(ui),ri2= μν2(ui),ri3= μν3(ui)。
1.2.4 模糊综合评价法
首先,根据各评判因素对水资源承载力影响程度的大小确定权重向量W;然后,采用加权平均算子(·,+)进行模糊合成,即根据权重向量W和R矩阵,将B = WR按普通矩阵计算规则即可求得水资源承载力的最终评判的结果向量;最后,根据V1、V2、V3分级指标对应的评分值a1、a2、a3,按下述公式(6)求得区域水资源承载力综合评分值a:

为了突出占优势等级作用,用bj的k次幂作为权重加权平均求结果,一般k值取为1[8]。
2 实证分析
以温州市为例,应用模糊综合评价方法进行水资源承载力的综合评价。
2.1 指标数据
查询已公布的温州市统计年鉴、温州市水资源公报以及温州大学图书馆的统计数据库等数据资源。可得以上9个指标从2007 — 2011年的原始数据,具体数据见表2。
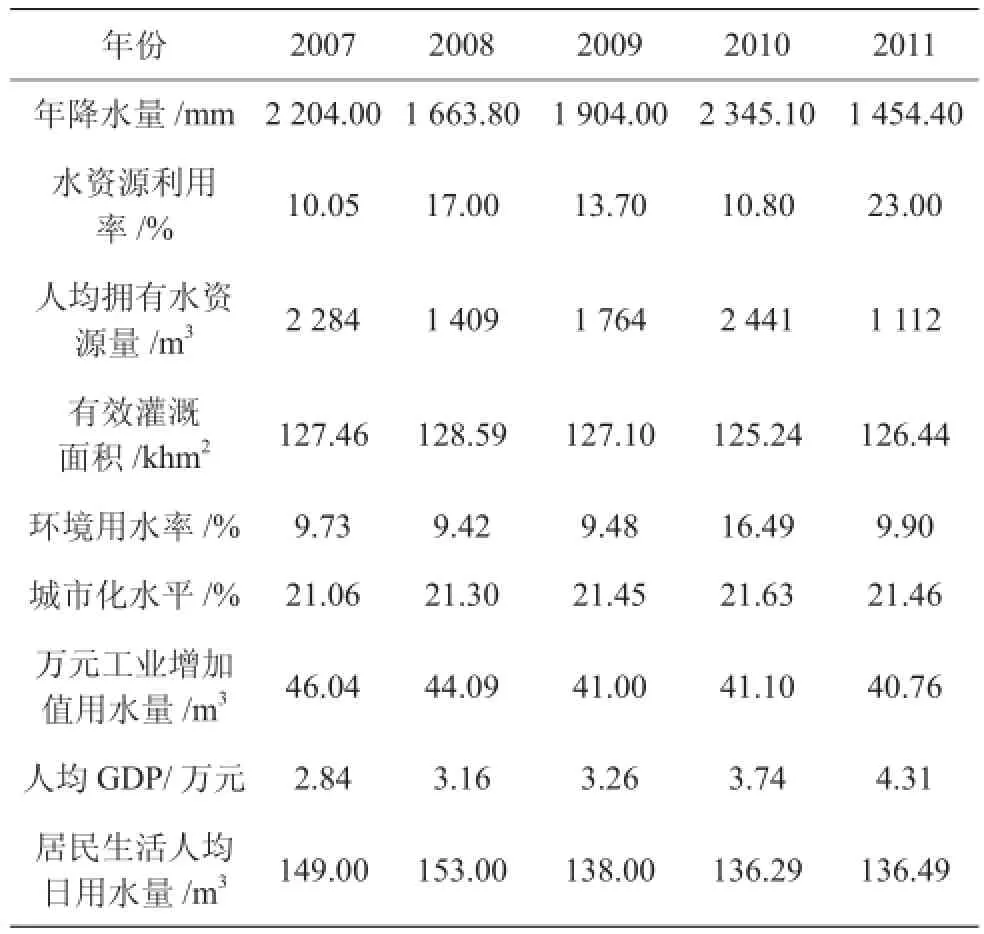
表2 各评判因素的原始数据表
2.2 结果分析
根据各评判因素对水资源承载力影响程度的大小,并借鉴相关水资源的评价标准以及一些专家学者的研究成果,本文给出各评判因素的 权重向量为W =(0.11,0.11,0.11,0.11,0.11,0.11,0.11,0.11,0.11)。利用1.2节中所述的水资源承载力模糊综合评价模型,采用Matlab软件进行编程计算,评价结果见表3。
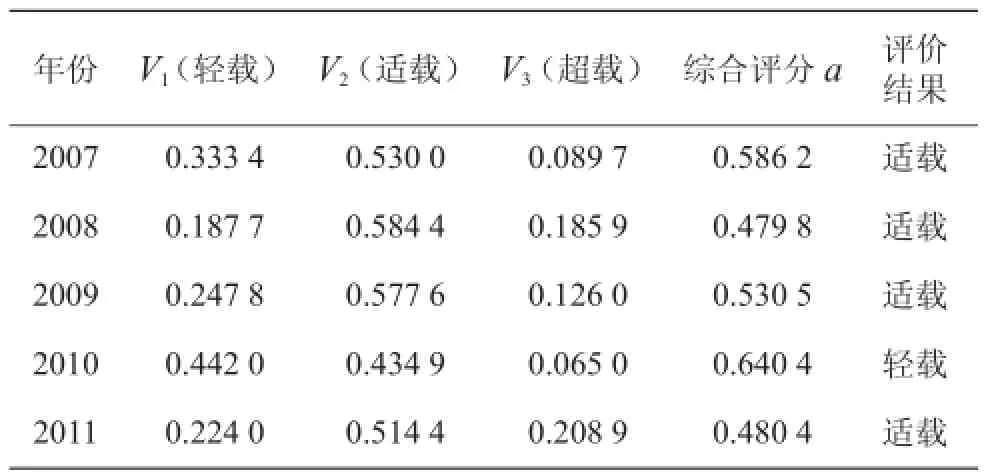
表3 温州市水资源承载力综合评价结果表
从表3可知,2007年的评价结果向量B =(0.330 4,0.530 0,0.089 7),所以2007年的水资源承载力是属于适载的,几乎无超载现象。当年的综合评价分值为0.586 2。同理,可以判断2008年温州市的水资源承载力是适载的,水资源开发利用已达一定规模,还有一定的开发利用的潜力。2009年的水资源承载力也是适载的,但是相比2008年,水资源承载力情况有所改善,综合评分值从2008年的0.479 8上升到0.530 5。2010年温州市的水资源承载力是这5 a中最好的,综合评分值高达0.640 4,对V1级的隶属度为0.442 0,大于V2、V3的隶属度0.434 9和0.065 0,究其原因发现2010年温州市的年降水量为2 341.5 mm,远高于其它年份。温州市2011年的水资源承载力对V2等级的隶属度为0.514 4,大于其余2个等级的隶属度,综合评分值0.480 4。
3 结论与建议
通过运用模糊综合评价法对温州市的水资源承载力现状及其动态趋势进行了分析。依据评价结果与分析,可以看出温州市2007 — 2011年水资源承载力状况良好,都是适载或者轻载的,无超载现象。从指标的角度出发,可以发现指标年降水量对水资源承载力的评价结果影响较大。所以,为了温州市能更好地应对自然气候的变化,减小干旱天气等对温州市水资源承载力的影响,维护温州市生态社会经济的可持续发展。
针对温州市的水资源状况特别提出以下几个建议:加强水体污染防治措施,改善水质;转变现有的粗放型经济增长方式,构建合理健康的社会生产关系;建设雨水集流工程和水源涵养区,缓解水资源供需矛盾等有效加强水资源承载力的建议。
通过运用模糊综合评价法对温州市的水资源承载力进行实证分析,发现评价指标选取的合理性以及模糊评判方法的确定(隶属度函数以及权重)对最终评价结果都有较大的影响。选取的指标要涉及水质和非常规水、评价结果要突出超载现象,这些都是值得今后进一步深入研究的问题。
[1] 1989年新疆水资源软科学课题研究组.新疆水资源及其承载力的开发战略对策[J].水利水电技术,1989(6):2 - 9.
[2] 夏军,朱一中.水资源安全的度量:水资源承载力的研究与挑战[J].自然资源学报,2002,17(3):262 - 269.
[3] 郭旋,冯利华.义乌市水资源承载力模糊综合评价[J].安徽农业科学,2008,36(8):3348 - 3349.
[4] 惠泱河,蒋晓辉,黄强,等.二元模式下水资源承载力系统动态仿真模型研究[J].地理研究,2001,20(2):191 - 198.
[5] 方国华,胡玉贵,徐瑶,等.区域水资源承载能力多目标分析评价模型及应用[J].水资源保护,2006,22(6):9 - 13.
[6] 周丽.基于多元统计分析的浙江省水资源承载力综合评价[J].浙江水利科技,2016(1):48 - 52.
[7] 张晓鹏,张鑫.基于模糊综合评价法的区域水资源承载力研究[J].中国农村水利水电,2009(7):18 - 21.
[8] 董小曼.基于模糊综合评判方法评价聊城市水资源承载力[J].水资源与水工程学报,2010,21(1):137 - 140.
[9] 何逢标.综合评价方法的MATLAB实现[M].北京:中国社会科学出版社,2010.
(责任编辑 郎忘忧)
Application of Fuzzy Comprehensive Evaluation in the Water Resources Carrying Capacity
ZHOU Li
(School of Mathematics & Information Science,Wenzhou University,Wenzhou 325035,Zhejiang,China)
Based on the introduction of fuzzy comprehensive evaluation,this paper selected 9 evaluation indexes and 3 classifi cation indexes,and built a fuzzy comprehensive evaluation model of the water resources carrying capacity.Taking Wenzhou city as an example,by using the fuzzy comprehensive evaluation method,the water resources carrying capacity of 2007 — 2011 in Wenzhou city was evaluated comprehensively.The results show that the water resources carrying capacity in Wenzhou city is in good condition,reaching the suitable load level or light load level,no over load level.The annual precipitation index has more infl uence on the evaluation results of water resources carrying capacity.Finally,some measures and suggestions were put forward to provide a scientifi c decision - making basis for eco - social - economic sustainable development in Wenzhou city.
water resources carrying capacity;fuzzy comprehensive evaluation;Wenzhou City
TV213
A
1008 - 701X(2017)02 - 0016 - 04
10.13641/j.cnki.33 - 1162/tv.2017.02.005
2016-10-03
浙江省科技厅软科学研究计划项目(2014C35079);浙江省统计局2014年度统计研究课题(编号23);浙江省教育厅高校科研计划项目(Y201120738)。
周 丽(1977 - ),女,讲师,硕士,主要从事水资源系统分析和应用统计等方面的研究。
