基于GM（1，1）模型的飞机故障数量预测方法

孙海霞，赵培仲，戚佳睿，夏毅锐

（海军航空工程学院青岛校区，山东青岛266041）

基于GM（1，1）模型的飞机故障数量预测方法

孙海霞，赵培仲，戚佳睿，夏毅锐

（海军航空工程学院青岛校区，山东青岛266041）

基于某型飞机年度故障数量的历史数据，运用灰色系统理论建立了GM（1，1）模型，对该飞机年度故障数量进行预测，并对模型精确度进行了验证。结果表明，所建的模型准确、有效，可以为飞机未来几年的故障数量预测提高有效的参考。

灰色GM（1，1）模型；预测；故障数量

0 引言

飞机的维修保障费用在其寿命周期费用中居主要地位，对军用飞机来说，使用维修费通常占寿命周期费用65%～80%。而飞机的年故障数量是决定年度维修费用的最主要因素，也是得出飞机维修保障需求规律的重要参数，精确预测其数量是提高装备维修效益和保障精确化水平的重要前提。由于飞机在服役年限内发生的故障数量具有很大的不确定性，且相关的数据信息较少，针对这一特点建模时以灰色理论为依据。

灰色系统建模，是在削弱原始信息随机性，建立灰色“模块”的基础上，应用微分拟合法直接将时间序列转化为微分方程的，建立的是抽象系统发展变化的动态模型。运用这种模型对系统进行分析，可以反映出系统内部机制变化过程的本质，可用以预测控制。灰色系统模型的一般形式为GM（h，n），它是h阶n个变量的微分方程，不同的h和n的GM模型，有不同的意义和用途。常用的预测模型为GM（h，1），即只有一个变量的GM模型。由于h越大，计算越复杂，且精度也不一定就高，因此h一般在3阶以下。本文选用h=1的GM（1，1）模型，即单序列一阶线形动态模型来估算飞机年度故障数量。

1 灰色GM（1，1）预测模型

1.1 模型的建立

GM（1，1）模型的实质是对原始数据做一次累加生成1-AGO，使生成的数据序列呈一定的规律性，再作一次累减生成，还原求出模拟值，并进行预测。其构建步骤如下：

（1）输入原始数列X（0）（非负序列），X（0）＝（x（0）（1），x（0）（2），…，x（0）（n））。

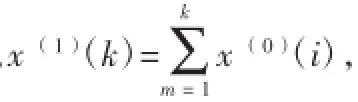
（3）Z（1）为X（1）的紧邻均值生成序列，Z（1）＝（z（1）（2），z（1）（3），…，z（1）（n）），式中，z（1）（k）=0.5x（1）（k）+0.5x（1）（k-1），k= 2，3，…，n。

（5）灰色微分方程为z（0）（k）+az（1）（k）=b。

（6）灰色微分方程的最小二乘估计满足a^=（BTB）-1BTY。

（9）检验误差。

1.2 模型的精度检验及预测值精度评估方法

为确保所建立的GM（1，1）模型的预测精度，还需要进行模型精度检验，模型精度检验常用的方法有残差检验、关联度检验和后验差检验等方法。本文选用残差检验和后验差检验方法进行检验，方法步骤如下。

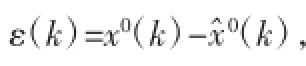
（3）预测值精度评估方法。上述两种检验方法中，相对误差和均方差比值越小越好，小误差概率越大越好。常用的精度等级评估参照表1。

2 基于GM（1，1）模型的某型飞机年度故障数量预测

2.1 GM（1，1）模型的建立

某型飞机2008～2013年的年故障总数量数据如表2所示。将以上数据输入灰色系统理论建模软件中，计算过程和结果如下。

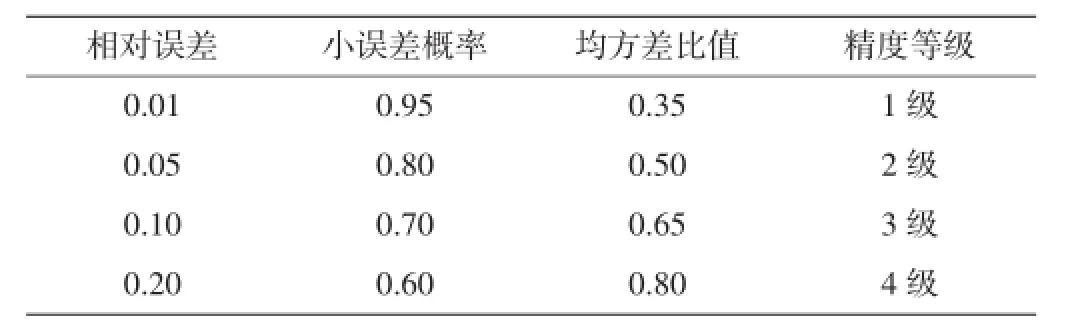
表1 GM（1，1）模型精度检验等级参照表

表2 某型飞机2008～2013年的年实际故障总数量

——Start——

第［1］步，原始序列的初始化

初始化后的序列：125，131，141，146，153，158

第［2］步，原始序列的1-AGO

1-AGO序列：125.00，256.00，397.00，543.00，696.00，854.00，

第［3］步，1-AGO的紧邻均值生成

紧邻均值生成序列：190.50，326.50，470.00，619.50，775.00

第［4］步，发展系数和灰色作用量的计算

第［5］步，模拟值的计算

125.00 ，132.96，139.08，145.48，152.18，159.18，

第［6］步，计算残差

残差=9.87

——End——

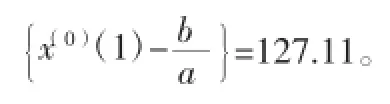
表3 该飞机年故障总数量预测值

2.2 模型精度检验（表4）

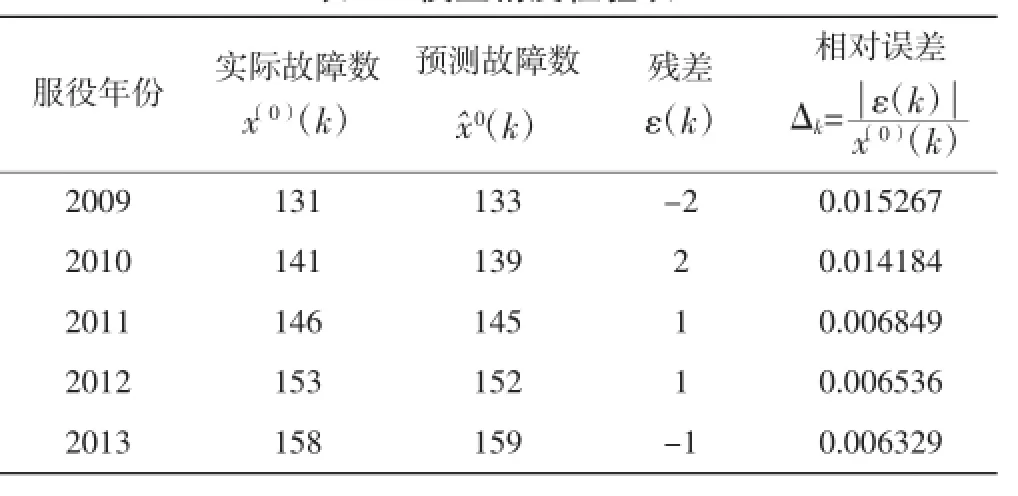
表4 模型精度检验表

对照表1可知，本模型的预测模拟精度等级为“一级”，满足精度要求。预测值与实际值的对比情况如表5所示，通过对比可以看出预测值与实际值相差很小，也说明模型的精度较高，能较好的预测未来几年发生的故障数量。

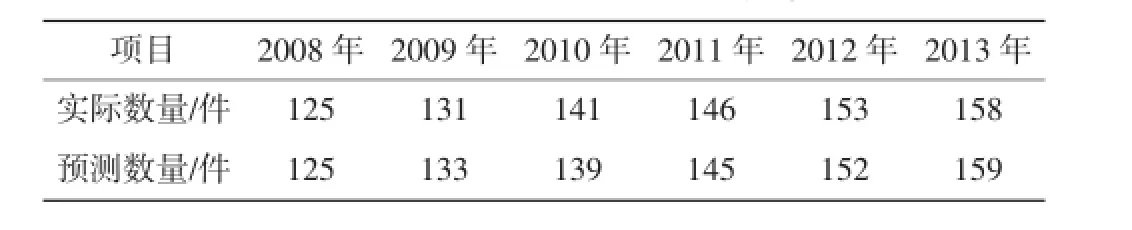
表5 某型飞机2008～2013年的年故障总数量

2.3 部件故障数量建模

在统计故障中，飞机的某些部件的故障较多。采用相同的原理和方法，亦可将故障数较多的部件进行建模分析预测。比如，发动机的年故障数量数据如表6所示。

表6 2008～2013年发动机部件的年故障数量

根据以上建立的预测模型，可以计算出发动机在2008～2013发生的年故障数（表7），还可以预测发动机在未来几年发生的故障数量，例如2014～2018年的故障总数分别为34，39，46，53。

表7 2008～2013年发动机部件的年故障总数量

通过对比预测值与实际值，可以看出预测值与实际值相差很小，亦说明模型的精度较高，能较好的预测未来几年发动机发生的故障数量。

3 结语

通过建立GM（1，1）模型，根据2008～2013年的故障统计数据，分别对年度飞机总的故障数和发动机部件的故障数进行了建模预测。通过精度检验及实际值与预测值的对比，可以看出本研究建立的预测模型具有较高的预测精度，符合实际的预测需求。

随着、装备服役年限的增加，真实的故障数据会不断增加。所以，根据新的数据，还可以采取新陈代谢的方法，进一步改进模型，提高预测的准确性。因为在实际中，装备自身的情况和日常的维护情况都会影响到装备的故障情况。装备和日常维护工作的情况都会随时间有不同的变化，因此，及时考虑新的数据是十分必要的。

［1］张恒喜，刘晓东，郭基联.飞机全寿命费用预测模型（ALCCE-2）研究报告［R］.西安：空军工程大学工程学院，1994.

［2］孙德全.飞机维修品质与维修性设计［M］.北京：中国人民解放军总后勤部司令部，1987.

［3］邓聚龙.灰色理论基础［M］.武汉：华中科技大学出版社，2002.

［4］徐凤建.GM（1，1）模型在装备维修保障成本预测中的应用［J］.电子产品可靠性与环境试验，2010，28（6）：14-17.

［5］陈郁红，刘军.灰色预测在无人机维修费用估算中的应用［J］.北京航空航天大学学报，2004，30（3）：214-216.

［6］刘建.航天型号使用维修费用的GM模型估算方法研究［J］.航天工业管理，2004（11）：17-20.

［7］陈勇.民用飞机维修成本分析与评估［D］.南京：南京航空航天大学，2006．

［8］范红军.军用飞机维修保障费用的GM（1，1）预测［J］.微计算机信息，2011，27（5）：126-127.

［9］白暴力，杨琳.飞机维修费用估算的分析［J］.空军工程大学学报（自然科学版），2005，6（5）：8-10.

［10］刘慕霄.改进GM（1，1）模型在舰船维修费用预测中的应用［J］.舰船电子工程，2010，30（12）：151-154.

〔编辑 凌瑞〕

E953

B

10.16621/j.cnki.issn1001-0599.2017.03.53