基于凸优化的图像隐藏信息重构方法

赵震震， 杨晓飞， 黄 俊， 刘书朋

(1.中国科学院 上海高等研究院 公共安全中心，上海 201210；2.上海大学 通信与信息工程学院，上海 200444)

基于凸优化的图像隐藏信息重构方法

赵震震1,2， 杨晓飞1， 黄 俊1， 刘书朋2

(1.中国科学院 上海高等研究院 公共安全中心，上海 201210；2.上海大学 通信与信息工程学院，上海 200444)

针对图像信息隐藏最不重要位(LSB)算法抗攻击性弱的缺点，提出了一种将凸优化的矩阵重建理论运用于所提取的隐密图像中的重建方法。对所提取的隐密图像作离散余弦变换(DCT)，使变换后的数据稀疏化，利用奇异值迭代算法重构数据，通过逆运算得到精度较高的隐秘图像，实验结果验证了方法的可行性。

最不重要位； 凸优化； 矩阵重建； 稀疏； 离散余弦变换

0 引 言

为了保证含有载体信息的图片信息能够在不可感知的情况下有效地传输[1～4]，研究在变换域中对信息隐藏和提取[5],通过置乱原始信息达到加密的目的。然而，在变换域下的图片信息隐藏虽然具有一定的鲁棒性，但是在嵌入位置的选择上具有先天的局限性，因此，可嵌入的信息量很少，且经过置乱的信息在传输过程中受到干扰，为隐密信息的提取带来更大的麻烦。此外，图片在变换域变换的同时，本身会缺少一部分信息，也为图片信息的隐藏带来不必要的信息缺失。

经典的最不重要位(least significant bits,LSB)算法相比于变换域的算法具有嵌入量大的优点，但是在传输过程中容易受到噪声等信息的干扰而导致提取的信息不精确。本文针对LSB的缺点，充分利用图片相邻像素点的相关性，依靠从压缩感知发展而来的凸优化的矩阵重建理论[6]，对提取到的二维图片信息进行稀疏化处理，利用凸优化的思想对二维图片信息进行重构，最终得到精度更高的传输结果。

1 空域下的LSB算法

对于256灰度的图像，每个像素值的灰度值ρ∈{0,1,2,…,255}，每一个像素值都可以用8 bit的二进制来表示。因此，灰度图像可以按照比特位分解为从高到低依次排列的βτ个位面，βτ∈{7,6,…,0}。对于一幅自然图像而言，相邻的灰度值具有很强的相关性，位面越高，对灰度值的贡献就越大，相邻比特位的相关性也就越强，而最低位面则表现类似于随机噪声，即最不重要比特位，为信息的隐藏提供了空间。

待嵌入的秘密消息比特序列为m={m1,m2,…,mL}，其中，L为比特序列的长度。载体图像像素集合c={c1,c2,…,cN}，其中N为像素个数。从集合c中选取L大小的一个子集cσ={cσ1,cσ2,…,cσL}(L≤N,1≤σk≤N,1≤k≤L)，并对子集中的所有元素做替换运算LSB(ck)=mk(1≤k≤L)，其中LSB(x)，表示x为最低有效位。

2 凸优化的矩阵填充理论

矩阵填充针对的问题是当矩阵中只有一小部分的数据值可知，而且可能含有噪声或者误差的情况下，如何准确合理地重建出整个矩阵。在文献[7]中，Candès在压缩感知的基础上，详细证明了什么样的矩阵可以重建以及在一定条件下的重建概率。假设待填充的矩阵是有信息冗余即低秩的，即其数据可以用一个低位的线性子空间表示[8]。矩阵填充的问题可以表示为

minrank(x)

subjecttoXij=Mij,(i,j)∈Ω

(1)

式中M为只观测到一部分元素的矩阵，X为待重建的矩阵，Ω为观测到的已知元素的下标的集合。这个数学公式的意义在于：将矩阵缺失的元素填充后，使得矩阵的整体结构尽可能好，即矩阵的秩尽可能低。然而，这是一个NP难问题，无法得到数学上的最优解[7]。由于一个矩阵的秩r与它非奇异值的个数相同，因此用矩阵的奇异值的和，即核范数，来近似代替矩阵的秩，于是式(1)可以优化为

min‖X‖*

subjecttoXij=Mij,(i,j)∈Ω

(2)

3 算法描述

3.1 离散余弦变换

离散余弦变换(DCT)属于正交变换，它将空间域变换到频域，将信号的能量集中到为数不多的中低频系数上。具体公式为：

DCT正变换

(3)

式中 0≤μ≤M-1,0≤v≤N-1,c(μ)和c(v)的表达式为

(4)

DCT反变换

(5)

式中A(i,j)为对应图像像素点的灰度值，Q(μ,v)为变换到DCT域后形成的矩阵的对应元素值。

3.2 奇异值分解

奇异值分解(SVD)是矩阵分解中非常重要的方法。通过奇异值分解，将一个非常复杂的矩阵用更小更简单的几个子矩阵相乘来表示，分解后的奇异值越大，代表这个元素越重要[11]。奇异值分解可以描述为

(6)

即A=UHVT，其中U为左奇异向量组成的矩阵，V为右奇异向量组成的矩阵，U和V中的向量均相互正交。其中,H除了对角线上的奇异值外，其它均为0，可表示为H=diag(σ1,σ2,σ3,…,σr)，r为矩阵A的秩。

3.3 算法设计

输入：图片载体矩阵EM×N待隐藏的图片矩阵CP×Q

1)将矩阵CP×Q转换为一维的向量W→。

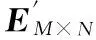
3)根据密钥，在X中找出嵌入隐藏信息的像素点，并提取出隐藏的信息，并最终生成C′P×Q，对该矩阵进行稀疏化处理，得到C″P×Q，并使Y0=0。

4)计算如下式子

Xk=Dτ(Yk-1),Yk=Yk-1+δkPΩ(E′-Xk)

当X=UHVT时，Dτ(X)=USτ(H)VT。δk为迭代步长，PΩ为投影算子，Sτ为收缩算子。

6)结束循环后，得到X，做DCT的逆变换和二值化处理，得到最终的隐藏信息X′。

4 实验结果与分析

文中采用经典的Lena图像作为载体图像，二值化图像作为待隐藏的信息。同时，模拟图像在传输过程中可能会受到的高斯噪声、椒盐噪声等的攻击，对重构图像的衡量标准为归一化相关系数(normalizedcoefficients,NC)和均方根误差(root-mean-squareerror,RMSE)。其中NC的公式定义如下

(7)

RMSE公式为

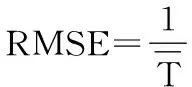
(8)

实验结果如图1。

图1 实验结果图

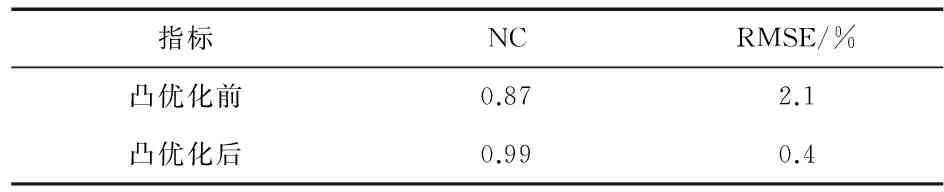
指标NCRMSE/%凸优化前0.872.1凸优化后0.990.4

从图1可以看出，由于嵌入隐藏信息的图像受到噪声的攻击，使得原有的图像含有很多不准确的像素点，以至于提取到的水印图像相比于原水印图像有很大误差。经过凸优化处理后，隐藏图像不精确的像素点大大减少。从表1可以看出，图片的NC从0.87提高到0.99，RMSE从2.1 %降低到0.4 %。实验结果达到了预期目标，验证了凸优化算法的可行性。

5 结 论

经过仿真实验验证：本文算法在加密图像受到噪声干扰的情况下，依旧能够较为精确地重构出原始隐密图像，相比于原始方法提高了提取图像与原始隐密图像的相似度，为图像信息隐藏提供了新的方法和思路。

[1] Kang H,Iwamura K.Information hiding method using best DCT and wavelet coefficients and its watermark competition[J].Entropy,2015,17(3):1218-1235.

[2] Abed F S,Mustafa N A A.A proposed technique for information hiding based on DCT[J].International Journal of Advancements in Computing Technology,2010,2:140-152.

[3] Yang J.Algorithm of image information hiding based on new anti-Arnold transform and blending in DCT domain[C]∥2010 12th IEEE International Conference on Communication Technology(ICCT),IEEE,2010:312-315.

[4] Wong K S,Ong S,Tanaka K, et al. Bitstream size suppression for DCT-based information hiding method[C]∥2011 Inter-national Symposium on Intelligent Signal Processing and Communications Systems(ISPACS),IEEE,2011:1-5.

[5] 张 健,任洪娥,陈 宇.基于均匀置乱与可逆隐藏的双重图像保密算法[J].传感器与微系统,2010,29(6):71-74.

[6] 彭义刚,索津莉,戴琼海,等.从压缩传感到低秩矩阵恢复: 理论与应用[J].自动化学报,2013,39(7):981-994.

[7] Candes E J,Recht B.Exact matrix completion via convex optimization[J].Foundations of Computational Mathematics,2009,9(6):717-772.

[8] 李 超.Toplitz矩阵重建的算法及实现[D].太原：太原理工大学,2015.

[9] Recht B.A simpler approach to matrix completion[J].Journal of Machine Learning Research,2009,12(4):3413-3430.

[10] Cai J F,Candes E J.A singular value thresholding algorithm for matrix completion[J].Siam Journal on Optimization,2010,20(4):1956-1982.

Image hiding information reconstructing method based on convex optimization

ZHAO Zhen-zhen1,2, YANG Xiao-fei1, HUANG Jun1, LIU Shu-peng2

(1.Public Security Center, Shanghai Advanced Research Institute,Chinese Academy of Sciences,Shangha,201210,China; 2.School of Communication and Information Engineering,Shanghai University,Shanghai 200444,China)

Aiming at shortcomings of weak attack resistance of image information hiding least significant bits(LSB)algorithm,a reconstructing method which applies matrix reconstructing theory based on convex optimization to extracted hiding image is proposed.The method makes discrete cosine transform(DCT)on extracted hiding image,to make transformed data spare,singular value iteration algorithm is used to reconstruct data and hiding image is obtained through inverse operation,feasibility of the method is verified by experimental result.

least significant bits(LSB); convex optimization; matrix reconstruction; spare; discrete cosine transform(DCT)

10.13873/J.1000—9787(2017)04—0054—03

2016—06—21

TP 391

A

1000—9787(2017)04—0054—03

赵震震(1990-)，男，硕士研究生，主要研究方向为图像处理。

杨晓飞(1975-)，男，通讯作者,博士，高级工程师，博士生导师，主要从事图像处理方面研究工作，E—mail:yxf@sari.ac.cn。