基于回归分析和小波变换的边坡变形组合预测研究

杨振兴,陈飞飞,马还援,李忠艳

(青海省水文地质工程地质环境地质调查院 青海省水文地质及地热地质重点实验室，西宁 810008)

基于回归分析和小波变换的边坡变形组合预测研究

杨振兴,陈飞飞,马还援,李忠艳

(青海省水文地质工程地质环境地质调查院 青海省水文地质及地热地质重点实验室，西宁 810008)

为有效地判断边坡变形的发展趋势,基于边坡变形的现场数据，首先利用回归分析和小波变换分解边坡变形数据的趋势项和误差项，并选取若干最优的分解数据进行组合确定边坡变形数据的趋势项和误差项，再利用BP和RBF神经网络对趋势项和误差项序列进行预测，得到单项预测的结果，最后研究分析了定权组合预测和非定权组合预测的效果。结果表明：在趋势项和误差项的分离过程中，不同分离方法的分离结果具有一定的差异，以6次多项式回归、5次及7次傅里叶回归和sym2小波变换的结果较好；同时，在单项预测中，分项预测的效果要优于传统的单项预测，验证了分项预测的有效性，并由组合预测的结果可知，2种组合预测的效果均较好，均很大程度上提高了预测精度，且非定权组合的预测精度要优于定权组合预测的精度。上述研究为边坡的变形预测提供一种新的思路。

边坡变形；回归分析；小波变换；组合预测；趋势项

1 研究背景

三峡工程是我国最重要的水利工程之一，由于施工条件的限制，使得在船闸修建的过程中，两侧采用了较陡的边坡形式，而边坡的变形是边坡稳定性的直接表现。所以，通过边坡的变形预测来判断边坡未来的变形趋势具有重要的研究价值。

在边坡的变形数据中，难免会包含有一定的误差信息，对变形预测具有一定的影响，有必要对其变形数据进行分离。已有相关学者在这方面进行了研究，如曹洋兵等[1]采用灰色系统模型分离了趋势项和误差项，并建立GM-ENN预测模型，实例验证其效果较好；许霄霄等[2]利用回归分析求解趋势项和误差项，并建立曲线回归-BP神经网络预测模型；杨哲峰等[3]利用小波去噪分解了基坑变形的趋势项和误差项，取得了良好的效果。同时，考虑到单项预测精度及其稳定性的不足，也有许多学者对组合预测进行研究，如黄惠峰等[4]利用方差倒数加权和误差倒数加权，对铁路的沉降变形进行组合预测，实例验证其效果较好；杨腾飞等[5]则利用2种赋权法对路基沉降变形进行预测，实例验证该方法也具有较好的效果；肖海平等[6]对某高边坡的变形进行了组合预测；董辉等[7]利用支持向量机对滑坡变形进行组合预测，验证了该方法的有效性。但是上述研究中，缺少对边坡变形的趋势项及误差项的分离研究，且未对多种趋势项的组合提取，也未对组合预测进行充分的研究分析。

因此，本文首先探讨多种回归分析及小波变换提取趋势项的效果，并创新性地以熵值为指标来评价趋势项提取的效果，且选取若干效果较好的趋势项及误差项的分离结果，以其熵值为基础，组合分解边坡变形的趋势项和误差项；同时，利用BP和RBF神经网络对趋势项和误差项进行预测，并对比本文分项预测结果和传统神经网络的预测结果；另外，探讨研究多种定权组合预测和非定权组合预测的效果；最后，对比分析不同预测方法的预测效果，为边坡变形的预测提供一定思路。

2 基本原理

2.1 论文思路

根据时间序列的基本原理，边坡的变形时间序列可分解为趋势项和误差项，其表达式为

Yt=Ut+Vt。

(1)

式中：Yt为边坡的变形时间序列;Ut为边坡位移趋势项;Vt为边坡位移误差项。

边坡的趋势项主要是受坡体岩性、边界条件及其力学性质等的影响，而误差项则主要受水力条件、局部外荷载及人为误差等因素的影响。因此，本文先构建回归分析和小波变换模型，分解边坡位移变形的趋势项和误差项，并利用变形数据的熵值来评价时序分解的效果，选取若干较优的时序分解方式，再以熵值为基础，组合确定最优的趋势项和误差项的分解，旨在提取最优的时序分解。

同时，在基于趋势项和误差项分解的基础上，构建BP神经网络及RBF神经网络的时间序列的预测模型，并利用定权及非定权2种方式对预测数据进行组合预测分析，旨在探讨不同组合预测模型的效果，进而选取最优预测模型。

2.2 趋势项提取模型

在边坡位移数据的处理过程中，选取回归分析和小波变换对边坡变形时序进行分解。回归分析以Matlab的Cftool工具箱为基础，采用最小二乘法进行回归，共选取4种回归模型，21种回归方法，即多项式回归模型、傅里叶回归模型、幂逼近回归模型及指数逼近回归模型，详见表1。

表1 回归分析函数Table 1 Functions of regression analysis models

在小波变换的应用过程中，处理过程具有离散特点，因此将小波变换的过程分解为如下步骤：

(1) 小波分解。基于小波函数构造的变换矩阵及分解层数，将原始时序进行分解。

(2) 阈值处理。根据不同的时序特点和小波分解特点，选取合适阈值及其选取方法，对各层小波变换进行阈值处理，最大程度保留原始信号。

(3) 小波重构。将经阈值处理后的各层小波频数进行重构，得到去噪后的变形时序，得到精度较高的边坡变形数据。

基于文献[3]的研究可知，在阈值的选取方法以硬阈值较好，阈值选取标准以启发式阈值更好，分解层数以7层较好，且Sym小波系的综合去噪效果要优于Db小波系的综合去噪效果。因此，本文小波变换过程中，采用上述参数进行小波变换。

在趋势项提取效果评价中，本文创新性地提出以熵值来作为提取效果评价的指标，即利用熵值法求解各趋势项提取方法的误差项熵值，熵值越大说明误差序列的无序性越高，进而反映出趋势项提取的效果较好。同时，基于不同趋势项提取方法的结果，选取若干较优的提取方法，以熵值为基础，求解各方法的相应权重，并将两者结合，最终求得综合性较强的趋势项和误差项。

2.3 组合预测模型

基于前文对边坡变形数据的分解，利用BP神经网络和RBF神经网络对各时序进行预测，对比分解前后不同的预测结果，旨在探讨分解趋势项预测对预测精度的提高程度。同时，进一步利用组合预测来克服单项预测精度及稳定性的不足，减小预测的系统误差[8]。

若单项预测结果为Yx=(y1x,y2x,y3x,…,ynx)，其中x代表预测方法的编号，n为预测节点的数目，且相应组合预测模型的权重向量P=[p1,p2,p3,…,pn],则组合模型的预测结果如式(2)所示，即

Y′=p1y1x+p2y2x+…+pnynx。

(2)

另外，本文的组合预测模型主要有2种类型，即定权组合预测和非定权组合预测，其中定权预测包含了特尔斐法[9]、CRITIC法及变异系数法，而非定权组合预测则是利用误差平方和倒数法、BP和RBF神经网络确定各非定权权值[10-11]。

图1 边坡位移变形Fig.1 Cumulative deformation curve of slope

图2 累计变形曲线斜率分布Fig.2 Slope distribution of cumulative deformation curve

3 实例分析

3.1 数据来源

基于前文的基本原理，本文以文献[12]中三峡永久船闸的高边坡位移监测数据为本文的数据来源，以验证本文思路的有效性。本文的边坡位移数据来源于三峡工程第三闸首位置，其监测数据详见图1。

同时，对各监测时间对应位置进行求导，得出边坡位移变形曲线的斜率分布，详见图2。由图2可知，变形曲线的斜率分布较为有规律，近似分为3个增长区间和2个减小区间，其中最大的增长斜率为2.48mm/月，而最小的减小斜率为-0.69mm/月。

3.2 趋势项提取

基于前文趋势项提取的相应原理，本文采用回归分析及小波去噪提取趋势项，对比不同的趋势项提取方法，为后文预测提供有效的基础数据。

3.2.1 回归分析趋势项提取

本文共采取4种回归模型，21种回归方法对边坡的变形监测数据进行趋势项分解，其相关计算结果详见表2。

表2 回归分析成果Table 2 Results of regression analysis

由表2可知，对比4种不同的回归模型，得出多项式回归、傅里叶回归及幂逼近回归的熵值期望相差不大，其中以傅里叶回归的效果为最优，而指数逼近回归的熵值期望最小，说明其趋势项提取的效果也最差，且4个回归模型的方差值均相差不大，幂逼近和指数逼近的回归效果要略优于多项式和傅里叶回归，这与各回归模型具有不同的回归方法数有关系，但各回归模型的稳定性均较好。同时，在多项式回归中，熵值随多项式次数的增加表现为先增加后减小的规律，其最大熵值为0.957 6，最小熵值为0.935 1；在傅里叶回归中，熵值分布的规律性不明显，其最大熵值为0.963 6，最小熵值为0.934 8；而幂逼近及指数回归的最值详见表2。综合上述回归分析的结果，选取6次多项式回归、5次及7次傅里叶回归的结果作为回归提取趋势项的结果。

3.2.2 小波变换趋势项提取

本文采用Sym小波系，共8个小波函数，对边坡的位移监测数据进行小波变换，相关变换参数已在前文进行设定，其相关计算结果详见表3。

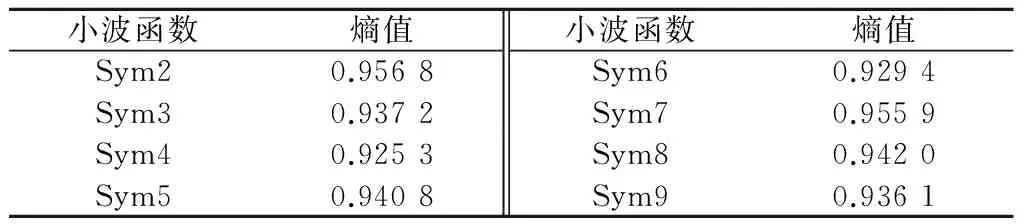
表3 小波变换成果Table 3 Results of wavelet transform

由表3可知，不同小波函数的信号变换结果具有一定的差异，也说明对不同小波变换结果进行讨论的必要性，其中以Sym2小波函数的小波变换效果最好，其熵值为0.956 8，Sym4小波函数的小波变换效果相对最差，其熵值为0.925 3，因此本文选取Sym2小波函数的小波变换的结果作为小波变换的最优提取趋势项的结果。

3.2.3 趋势项的组合确定

基于前文的趋势项提取探讨，本文选取6次多项式回归、5次及7次傅里叶回归、Sym2小波函数变换的结果作为本文趋势项提取的基础，以上述4种提取方法的熵值为基础，求解各方法的相对权重，经计算其权重依次为0.249 4,0.250 4,0.251 0,0.249 2，结合前文各分解方法的结果及其相应权重，求得综合趋势项及误差项，如表4所示。

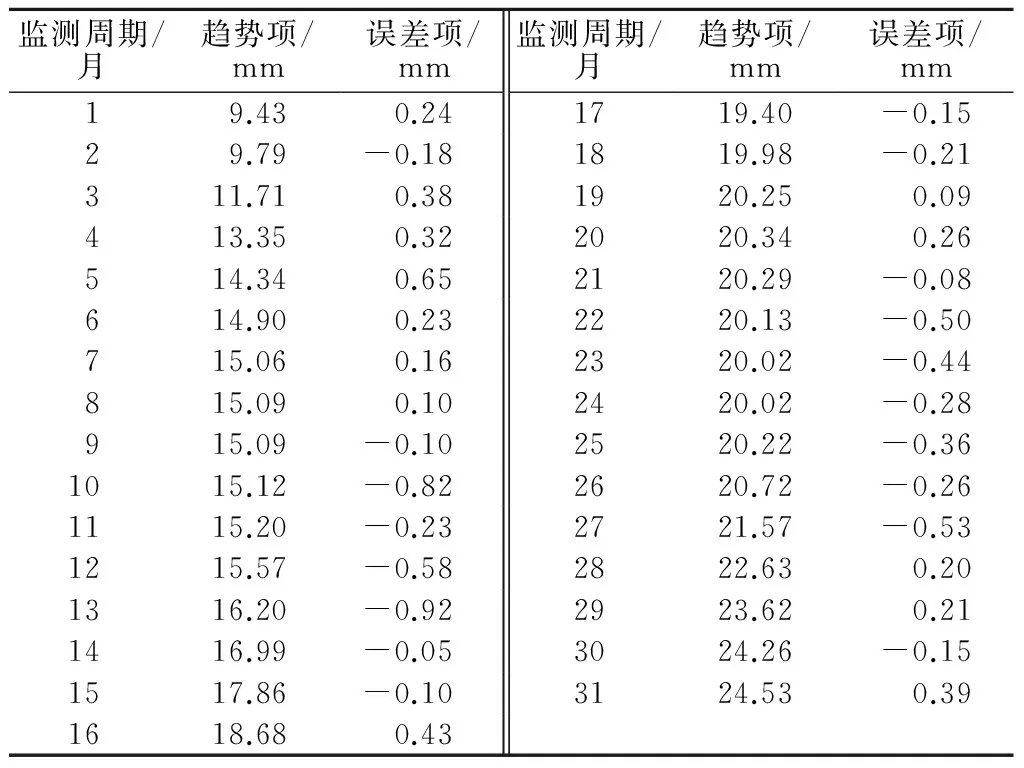
表4 时序分解成果Table 4 Results of time series decomposition

综合上述分析，得出在边坡位移趋势项及误差项分离过程中，不同的分离方法具有不同的效果，体现了对最优提取方法探讨的必要性；同时，本文创新性地提出以误差项熵值作为分离效果的评价标准，为后期分离的理论研究提供了一种思路。

3.3 边坡位移的组合预测

3.3.1 单项预测分析

基于前文回归分析及小波去噪对趋势项及误差项的分离研究，再采用BP神经网络和RBF神经网络对各时序进行预测，其预测结果详见表5。

由表5可知，本文分项预测相对误差精度的绝对值均在2%以内，而传统预测的相对误差多数集中在2%～3%之间，得出本文分项预测的精度较传统预测的精度提高了近一倍；同时，BP神经网络与RBF神经网络之间也具有一定的差异，表现为BP神经网络的预测精度要略高于RBF神经网络的预

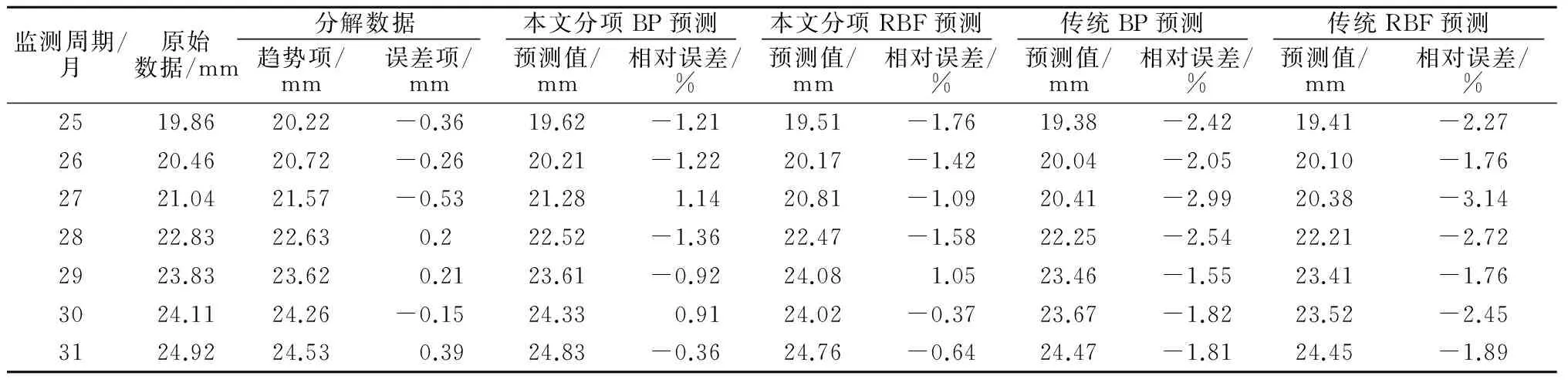
表5 单一预测结果Table 5 Prediction results of single term

测精度。综合各预测结果可知，预测精度均较高，这为此后进行的组合预测及趋势判断奠定了可靠的数据基础，也从侧面反映出本文预测方法的适用性和有效性。

表8 不同方法的残差平方和对比Table 8 Comparison of residual sum of squares in different methods

3.3.2 定权组合预测

采用特尔斐法、CRITIC法和变异系数法进行定权组合预测，并利用期望及方差评价组合预测的效果，结果详见表6。

表6 定权组合预测结果分析
Table 6 Analysis of the forecast result of fixed weight combination

权值方法统计值本文定权组合预测传统定权组合预测误差/mm相对误差/%误差/mm相对误差/%特尔斐法CRITIC法变异系数法期望0.1270.5970.4932.216方差0.0250.5420.0080.207期望0.1330.6230.4972.232方差0.0240.5240.0080.209期望0.1200.5620.4972.230方差0.0270.5870.0080.209

由表6可知，3种定权组合预测结果的期望和方差差异不大，说明3种定权组合预测在本文实例应用中的效果基本一致，其中变异系数法的预测结果最好，其次是特尔斐法的预测结果，最后是CRITIC法的预测结果；而在传统定权组合预测中，以特尔斐法的预测结果最好，其余2种组合预测具有相同的预测结果。对比本文定权组合预测和传统定权组合预测的结果可知，在预测结果的期望方面，传统预测的期望值要比本文预测的期望值大3倍左右，说明本文定权组合预测较传统定权组合预测对预测精度具有较高的提高；在预测结果的方差方面，传统定权组合预测的方差值要小于本文定权组合预测的方差值，说明传统定权组合预测结果的稳定性要优于本文定权组合预测结果的稳定性。

3.3.3 非定权组合预测

同时，本文再采用误差平方和倒数法、BP和RBF神经网络法求解单项预测的非定权权重，也利用预测结果的期望及方差评价预测结果，结果详见表7。

表7 非定权组合预测结果分析
Table 7 Analysis of the forecast result of non-fixed weight combination

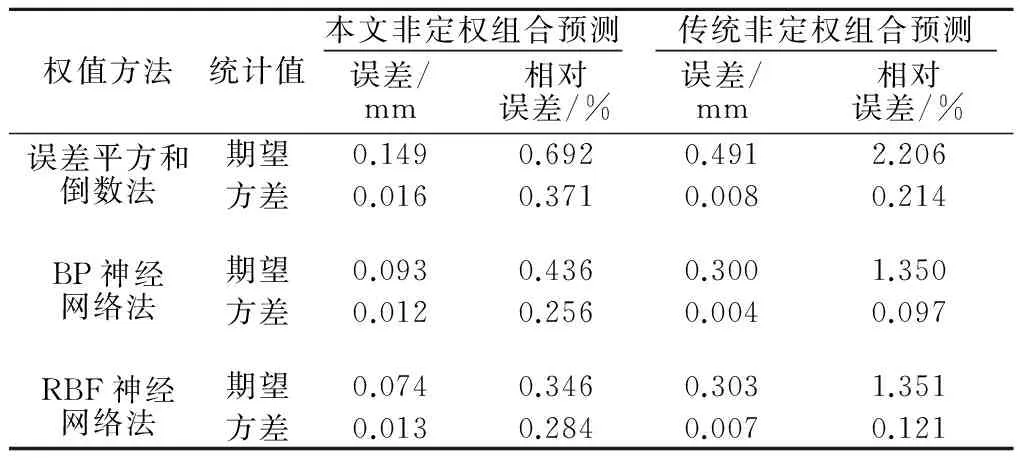
权值方法统计值本文非定权组合预测传统非定权组合预测误差/mm相对误差/%误差/mm相对误差/%误差平方和倒数法BP神经网络法RBF神经网络法期望0.1490.6920.4912.206方差0.0160.3710.0080.214期望0.0930.4360.3001.350方差0.0120.2560.0040.097期望0.0740.3460.3031.351方差0.0130.2840.0070.121

由表7可知，对比不同非定权的组合预测结果，得出2种神经网络法的预测结果要优于误差平方和倒数法的预测结果，且2种神经网络方法的预测结果差异不大，说明运用神经网络的非定权组合预测具有较好的效果；同时，对比本文非定权组合预测和传统非定权组合预测的结果可知，在预测结果的期望方面，传统预测的期望值要比本文预测的期望值大3倍左右，说明本文非定权组合预测较传统非定权组合预测对预测精度也具有较高的提高；在预测结果的方差方面，传统非定权组合预测结果的稳定性要优于本文非定权组合预测结果的稳定性。

3.3.5 预测结果对比分析

以残差平方和为评价指标，对比分析各预测方法的特点，相关计算结果详见表8。由表8可知，在单项预测中，本文的分项预测结果要明显优于传统的预测结果，且BP神经网络的预测精度要高于RBF神经网络的预测精度；同时，在定权组合预测中，本文分项定权组合预测的精度较单项预测均有较大的提高，且3种定权组合预测结果之间的差异不大，而传统定权组合预测的精度则介于2种单项传统预测之间；另外，在非定权组合预测中，3种非定权组合预测精度均优于定权组合预测的精度，其中误差平方和倒数法对误差精度的提高不明显，而2种神经网络非定权组合预测方法对误差精度的提高较显著。综合上述，得出组合预测均很大程度上提高了预测精度，且非定权组合预测的效果要优于定权组合预测。

4 结 论

(1) 在趋势项和误差项的分离过程中，不同提取方法的差异性较大，说明在趋势项的提取过程中，有必要对趋势项的提取效果进行评价。

(2) 对比单项预测的结果，得出本文分项预测的精度较传统预测的精度提高了近一倍，验证了本文预测方法的有效性。

(3) 定权组合预测比单项预测的精度高，说明定权组合预测的效果较好，且本文定权组合预测精度也高于传统定权组合预测精度，进一步说明本文预测方法的有效性。

(4) 非定权组合的预测精度高于定权组合预测的精度，说明非定权组合预测能提高预测精度。

(5) 综合对比各预测结果，得出本文预测模型对提高预测的精度和稳定性具有较好的效果。

[1] 曹洋兵,晏鄂川,谢良甫. 考虑环境变量作用的滑坡变形动态灰色-进化神经网络预测研究[J]. 岩土力学,2012,33(3):848-852.

[2] 许霄霄,牛瑞卿,叶润青,等. 基于外因响应的滑坡位移预测模型研究[J]. 长江科学院院报,2013,30(7):42-47.

[3] 杨哲峰,罗 林,贾东彦,等. 基于小波去噪的深基坑变形预测研究[J]. 人民长江,2014,45(19):41-46.

[4] 黄惠峰,张献州. 高速铁路沉降变形的组合预测方法[J]. 测绘工程,2014,23(9):48-51.

[5] 杨腾飞,施 昆,汪奇生. 两种客观赋权法及其在确定组合预测权重中的应用[J]. 测绘工程,2014,23(7):59-61.

[6] 肖海平,杨旺生,肖 岚,等. 基于组合预测模型的露天矿高陡边坡滑坡变形研究[J]. 金属矿山,2014,49(4):169-171.

[7] 董 辉,傅鹤林,冷伍明. 滑坡变形的支持向量机非线性组合预测[J]. 铁道学报,2007,29(1):132-136.

[8]曹成度. 高速铁路线下工程沉降变形组合预测探讨[J]. 铁道勘察,2012,38(4):1-3,16.

[9] 罗晓霞,王玉婷,郭 岚. 基于组合赋权法的土地资源定级因素因子权值的确定[J]. 西安科技大学学报,2015,35(1):115-119.

[10]俞俊平, 陈志坚, 武立军,等. 基于蚁群算法优化支持向量机的边坡位移预测[J]. 长江科学院院报, 2015，32(4):22-27.

[11]郭海庆, 张 敏, 黄 涛,等. 基于时移小波-灰色理论的边坡位移预测模型研究[J]. 长江科学院院报, 2015, 32(9):146-152.

[12]刘湘平,谢学斌,罗一忠. 边坡非线性位移预测的动力系统自记忆模型[J]. 岩土工程学报,2010,32(10):1535-1542.

(编辑：占学军)

Combinatorial Forecasting of Slope Deformation Based onRegression Analysis and Wavelet Transform

YANG Zhen-xing,CHEN Fei-fei,MA Huan-yuan,LI Zhong-yan

(Hydrogeological and Geothermal Geological Key Laboratory of Qinghai Province, Hydro Geology and Engineering Geology and Environmental Geology Survey Institute of Qinghai Province, Xining 810008，China)

In order to effectively estimate the variation trend of slope deformation, we employed regression analysis and wavelet transform to decompose the trend term and error term of slope deformation. In subsequence we selected data of optimal decomposition and predicted series of trend term and error term by using BP and RBF neural network. Then, we obtained the forecast results of single term and analyzed the forecast results of fixed weight combination and non-fixed weight combination. Results showed that the results of decomposing trend term and error term by different methods are different.Among the methods, polynomial regression with power of six. Fourier regressionwith power of five and seven and wavelet transform of sym2 have better results. Moreover, partial prediction is prior to conventional prediction of single term, which verifies the effectiveness of partial prediction in the present research. According to combinatorial forecasting results, fixed weight and non-fixed weight both obviously improved prediction accuracy, and the prediction accuracy of the latter is better than that of the former.

slope deformation; regression analysis; wavelet transform; combination forecasting; trend term

2016-02-01；

2016-03-28

杨振兴(1981-)，男，河北承德人，工程师，研究方向为地质灾害防治工程勘察设计及地质灾害防治技术，(电话)13519784119 (电子信箱) 89173786@qq.com。

10.11988/ckyyb.20160101

2017,34(4):38-42,51

TU45

A

1001-5485(2017)04-0038-05