具有交叉感染的2种菌株对逼近模型分析

秦文惠，张菊平

(中北大学理学院，山西太原 030051)

具有交叉感染的2种菌株对逼近模型分析

秦文惠，张菊平

(中北大学理学院，山西太原 030051)

为了研究具有一般接触率和用于治疗的SIS对逼近模型及其动力学性质，针对2种菌株是否可以独立生存，建立了一个在规则网络上2种菌株有交叉感染的SIS对逼近传染病模型。根据二项分布，利用节点的状态相关系数得到一个12维系统，计算出模型的基本再生数，得出无病平衡点的局部稳定性，进而获得了无病平衡点不稳定的阀值。通过理论分析和数值模拟得出模型的无病平衡点无条件存在，即不稳定。在研究了2种菌株独立存在以及共同生存的条件后，可以看出2种菌株可以独立生存，也可以相互感染。高维(12维)系统的引入，使得对逼近模型既能模拟疾病的传播机制又能捕捉到疾病传播所在种群的网络结构，因此将对逼近模型应用到多菌株疾病的传播中具有一定价值。

稳定性理论；交叉感染；对逼近；阈值；稳定性

引起传染病的病原体的表现形式有许多种，引起同一种传染病的病原体的不同表现形式称为不同的菌株，如已测得的引起细菌性肺炎的肺炎球菌有60多种形式[1]。然而在处理方程时，会出现不封闭的情况。因此，通常情况下对所出现的三元组方程用相应的对逼近的方法进行封闭处理[2]，对逼近模型不仅考虑个体相关性和其差异，而且也体现个体特征。在过去的几十年里，对逼近模型已经得到了广泛研究。例如：MATSUDA等[3-4]使用空间相关性对逼近计算的方法，研究了静止状态下关于出生、死亡和迁移率的晶格生态模型；BAUCH等[5-7]建立了susceptible-infected-susceptible(SIS)流行病的对逼近模型,而且根据此模型进一步给出了基本再生数。THOMSON等[8-9]在不考虑出生和死亡的情况下，在空间异构晶格的网络中建立了SIS传染病模型的逼近有效性评估空间。然而，KEELING[10]建立的对逼近模型没有考虑出生和死亡,而是考虑了相关的种群, 在研究群体水平的传染病模型时，由于不同的个体往往处于不同的状态，为了刻画网络节点状态之间的相关性，KEELING在文献[10]中提出了刻画节点状态相关性的相关系数以及同配系数CAB并获得基本的繁殖数量。

本研究在规则网络下应用稳定性理论探讨SIS传染病的对逼近模型，基于假设感染邻居个体的数量满足二项分布[11]，并将这个理论引入到两菌株对逼近模型中。目前已经引用了大量的对逼近模型来分析像天花、风疹、乙型肝炎等由一种菌株引起的流行病问题。纵观以上的传染病动力学方面的研究工作[3,7-12]，还有许多传染病的病原体是由多种菌株交叉感染共同作用引起的，如肺结核、艾滋病、登革热、肺炎链球菌等。已测得的引起艾滋病HIV的病毒有很多种，而且每年还有新的病毒被发现。对具有多菌株的病原体所引起的传染病来说，研究相应的控制方法很困难，即使接种疫苗，效果也不见好转[9-15]。因此，多菌株传染病动力学的数学建模与研究引起许多科研人员的兴趣，但是这方面的研究

还相对较少。对上述假设，很好地获得了一个12维系统的对逼近模型[2]，并进一步讨论无病平衡点的稳定性及边界平衡点的存在性。

1 模型的建立

将总人口(N)分为4类: 易感者(S), 被第1种菌株感染的染病者(I1), 被第2种菌株感染的染病者(I2), 同时被第1种和第2种菌株交叉感染的染病者(I12), 其在t时刻的数量分别用[S],[I1],[I2],[I12] 表示。假设βi表示第i种菌株感染的染病者Ii与易感者接触的传染率(i=1,2)，γi表示每类染病者的恢复率(i=1,2,3)，τ1表示被第1种菌株感染的染病者I1与被第2种菌株感染的染病者I2接触的传染率，τ2表示被第2种菌株感染的染病者I2与被第1种菌株感染的染病者I1接触的传染率，建立具有交叉感染的两菌株对逼近动力学模型，如图1所示。

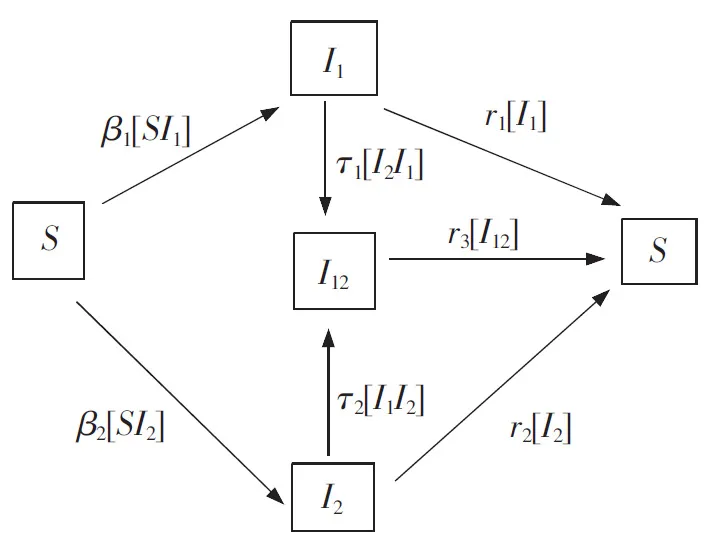
图1 交叉感染的两菌株对逼近模型流程图Fig.1 Flow chart of approximation model of two strains of cross infection

(1)

由于N(t)=[S(t)]+[I1(t)]+[I2(t)]+[I12(t)]=0,所以总人口始终保持一个常数，令[S(t)]+[I1(t)]+[I2(t)]+[I12(t)]=N,考虑无聚类节点的规则网络, 假设每个节点的邻居数为n, 节点的染病者邻居满足二项分布, 参考文献[11]可得：

A,B,C∈{S,I1,I2,I12}。

其他类似。

利用网络的总规模不变及规则网络的平衡条件：

[I12I12]+[SS]+[I1I1]+[I2I2]+2[SI1]+2[SI2]+2[SI12]+2[I1I2]+2[I1I12]+2[I2I12]=nN,

将系统(1)转化为系统(2):

(2)

为了研究模型(2)的性态, 引入刻画网络节点状态之间的相关性, 由文献[12]可得：

则有：

因此, 系统(2)转化为系统(3):

(3)

显然, 系统(3)的正向不变集为

0≤[I1]+[I2]+[I12]≤N,

2 平衡点的稳定性分析

系统(3)总存在无病平衡点E0=(0,0,0,0,0,0,0,0,0,0,0,0), 则在无病平衡点E0处的雅可比矩阵为

其中，a44=(n-2)β1,a55=(n-2)β2。

该矩阵对应的特征方程为

(λ+γ1)(λ+γ2)(λ+γ3)(λ-a44)×

(λ-a55)(λ+γ3)(λ+(τ1+τ2))×

(λ+γ1)(λ+γ2)(λ+2γ3)(λ+γ3)=0。

假设n>2，则n-2>0，所以(n-2)β2>0，且(n-2)β1>0。故特征方程的特征根中具有2个非负实部的根, 从而无病平衡点E0不稳定。

定理1 系统(3)的无病平衡点E0无条件存在，并且是不稳定的。

下面讨论边界平衡点的存在性。

i)当a>0,b<0,c>0时，系统(3)存在第1种菌株的一个边界平衡点；

ii)当a<0,b<0,c>0时，系统(3)存在第1种菌株的一个边界平衡点。

证明 令[I2]=0,[I1]≠0,则[I12]=0。可得：

则系统(3)满足：

(4)

解得：

(5)

(6)

将式(5)和式(6)代入式(4)中的第2个式子, 整理得：

a([I1])2+b[I1]+c=0。

其中：

下面对参数a,b和c的符号分别进行讨论。

i)当a>0,b<0,c>0时，a，b，c的符号如下：

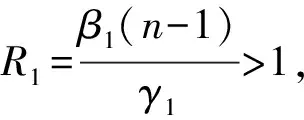
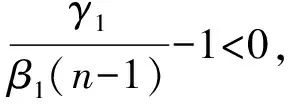
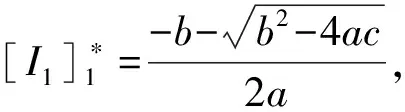
ii)当a<0,b<0,c>0时，a，b，c的符号如下：

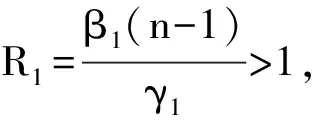
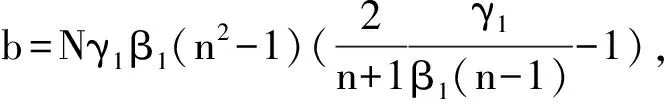
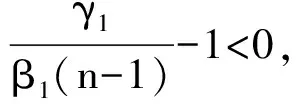
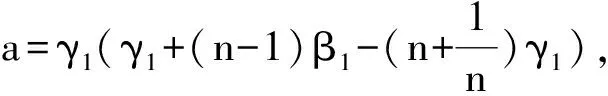
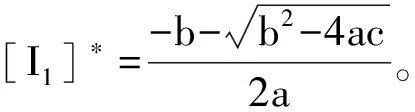
综上所述, 可概括为表1。

表1 根的情形

i)当a>0,b<0,c>0时，系统(3)存在第2种菌株的一个边界平衡点；

ii)当a<0,b<0,c>0时，系统(3)存在第2种菌株的一个边界平衡点。

该定理的证明类似于定理2, 即与第1种菌株边界平衡点存在性的证明对称，这里不再说明。

定理4 当R1>1,R2>1时，系统(3)存在正平衡点。

3 数值模拟

在理论上讨论系统(3)的无病平衡点和边界平衡点的存在性的基础上，本节将分析系统(3)以β1,β2,γ1,γ2,n为参数时平衡点的个数及类型[16-17]。

例1 当R1>1时, 系统(3)的模拟结果如图2所示，固定参数如下。

图2 a)中：n=3,γ1=0.01,β1=0.05,N=700,β2=0.05,γ2=0.1,τ1=0.05,τ2=0.05,γ3=0.15。

图2 b)中：n=3,N=700,γ1=1.167,β1=0.9,β2=0.5,γ2=1.167,τ1=0.05,τ2=0.05,γ3=0.08。

图2 当R1>1时，系统(3)的仿真结果Fig.2 Simulation results of the system (3) when R1>1

例2 当R1>1且R2>1时，系统(3)存在正平衡点的模拟结果如图3所示。固定参数如下。

图3 a)中：n=3，γ1=0.01，β1=0.05，β2=0.2，γ2=0.1，N=700，τ1=0.5，τ2=0.05，γ3=0.15。

图3 b)为图3 a)的放大图，表明地方病平衡点在R1>1且R2>1时是稳定的。

图3 当R1>1且R2>1时，系统(3)的仿真结果Fig.3 Simulation results of system (3) when R1>,R2>1

4 结 语

本文建立了一个考虑2种菌株具有交叉感染的对逼近传染病模型，模型中节点的染病者邻居遵循二项分布。通过分析对逼近传染病模型获得了一个12维方程组，由该系统(3)得到了基本再生数R0及无病平衡点E0的存在性。模型的无病平衡点E0无条件存在，并且是不稳定的，当R1>1,R2>1时，系统可能出现正平衡点。因此，基本再生数R0不再是模型的一个阈值。通过数值模拟证实了分析结果。从定理以及数值模拟的结果来看，两种菌株可以独立生存，且交叉感染后不会影响各自的性态。

/References:

[1] AHMED E, EL-SAKA H.On multi-strain model for Hepatitis C[J]. Nonlinear Biomedical Physics ,2011,5(1)：1-3.

[2] KEELING M J , EAMES K T. Networks and epidemic models[J]. Journal of the Royal Society Interface, 2005,2 (4):295-307.

[3] MATSUDA H, OGITA N, SASAKI A, et al. Statistical mechanics of population the lattice Lotka-Volterra model[J]. Progress of Theoretical Physics,1992, 88 (6):1035-1049.

[4] WU Qingchu, SMALL M, LIU Huaxiang,et al.Superinfection behaviors on scale-free networks with competing strains[J]. Journal of Nonlinear Science, 2013,23(1):113-127.

[5] BAUCH C T. The spread of infectious diseases in spatially structured populations: An invasory pair approximation[J]. Mathematical Biosciences,2006,198 (2):217-237.

[6] ZOU Shaofen, WU Jianhong, CHEN Yuming. Multiple epidemic waves in delayed susceptible-infected-recovered models on complex networks[J]. Physical Review E, 2011,83(5Pt2):056121.

[7] JIN Zhen, SUN Guiquan .Epidemic models for complex networks with demographics[J]. Mathematical Biosciences and Engineering Mbe,2014,11(6):1295-1317.

[8] THOMSON N A, ELLNER S P. Pair-edge approximation for heterogeneous lattice population models[J]. Theoretical Population Biology,2003,64 (3):271-280.

[9] PICCARDI C, COLOMBO A, CASAGRANDI R. Connecti-vity interplays with age in shaping contagion over networks with vital dynamics[J]. Phys Rev E Stat Nonlin Soft Matter Phys,2015,91(2):22809.

[10]KEELING M J.The effects of local spatial structure on epidemiological invasions[J]. Proc Biol Sci, 1999,266(1421):859-867.

[11]Morris J A. Representing spatial interactions in simple ecolo-gical models[J]. University of Warwick, 1997.

[12]ZHANG X, SUN G Q, ZHU Y X,et al. Epidemic dynamics on semi-directed complex networks[J]. Mathematical Biosciences, 2013,246(2):242-251.

[13]董亚丽，乔志琴.两种基因类型的丙肝传染病混合模型的动力学分析[J].河北工业科技，2017，34(1)：1-6. DONG Yali,QIAO Zhiqin.Dynamic analysis of mixture model about Hepatitis C Virus two genetic types[J].Hebei Journal of Industrial Science and Technology,2017,34(1):1-6.

[14]王娟,周学勤,李学志.一类具有接种疫苗和再次感染的传染病模型分析[J].数学的实践与认识, 2011,41(14):223-228. WANG Juan,ZHOU Xueqin, LI Xuezhi.Analysis for an epidemic model with vaccination and re-infection[J].Mathematics in Practice and Theory, 2011,41(14):223-228.

[15]李梁晨，徐瑞.一类具有细胞感染年龄和一般饱和和感染率的病毒感染动力学模型的稳定性分析[J].河北科技大学学报，2016,37(4):349-356. LI Liangchen, XU Rui. Stability analysis of a viral infection dynamics model with infection age of cells and general satu-rated infection rate[J].Journal of Hebei University of Science and Technology, 2016,37(4):349-356.

[16]BRITTON F C N F. On the dynamics of a two-strain influenza model with isolation[J]. Mathematical Modelling of Natural Phenomena, 2012,7(3):49-61.

[17]XIAO Yanyu, ZOU Xingfu. Can multiple malaria species co-persist[J]. Siam Journal on Applied Mathematics,2013,73(1):351-373.

Analysis of pair approximation model of two strains with the cross infection

QIN Wenhui, ZHANG Juping

(School of Science, North University of China, Taiyuan, Shanxi 030051, China)

To study the dynamics of pair approximation SIS model with general comtact rate and treatment.The pair approximation SIS model with a cross infection two strains are established in this paper in view of the two strains could live independently. We got a 12d system using the node status correlation coefficient based on the binomial distribution. In addition, we concluded that the local stability of the disease-free equilibrium by calauating the model of the basic reproductive number, and then, the unstable threshold of disease-free equilibrium is found. Finally, model of the disease-free equilibrium existenced unconditionally and it namely is not stable through theoretical analysis and numerical simulation. The conditions of two strains exist independently and the common survival are studied in this paper, and then, we concluded that two strains can live independently, and also be infected with each other. The high dimensionality (12) system is studied. The approximation model not only simulate the spread of disease mechanism but also capture the spread of disease in populations of network structure. So it has a certain value that applying the approximation model to many strains of the spread of disease.

stability theory; cross infection; pair approximations; threshold; stability

1008-1534(2017)02-0103-07

2016-12-12;

2017-02-12；责任编辑：张 军

国家自然科学基金(11301491)；山西省青年科学基金(2011021001-2)

秦文惠(1989—)，女，山西忻州人，硕士研究生，主要从事生物数学方面的研究。

张菊平副教授。E-mail:zhangjuping@nuc.edu.cn

O175.1

A

10.7535/hbgykj.2017yx02005

秦文惠，张菊平.具有交叉感染的2种菌株对逼近模型分析 [J].河北工业科技,2017,34(2):103-109. QIN Wenhui, ZHANG Juping.Analysis of pair approximation model of two strains with the cross infection[J].Hebei Journal of Industrial Science and Technology,2017,34(2):103-109.