装甲钢温度-组织-应力耦合本构模型的建立及在焊接模拟中的应用

孙玉杰， 崔青春， 韩璇璇， 石春明

(西北机电工程研究所, 陕西 咸阳 712099)

装甲钢温度-组织-应力耦合本构模型的建立及在焊接模拟中的应用

孙玉杰， 崔青春， 韩璇璇， 石春明

(西北机电工程研究所, 陕西 咸阳 712099)

装甲钢焊接热循环过程中固态相变对焊接残余应力的演变及大小有着重要影响，而现有的有限元软件本构模型无法考虑固态相变的作用。在传热学、固态相变理论和连续介质力学的基础上，建立了温度- 组织- 应力耦合的本构模型，本构模型中综合考虑了固态相变引起的体积变化、力学性能变化和相变塑性对焊接残余应力的影响，采用ABAQUS子程序UMAT通过二次开发将该本构模型嵌入通用有限元软件中，对装甲钢平板对接焊进行研究，获得了装甲钢焊接热循环过程中温度、组织及残余应力变化规律。研究结果表明：装甲钢平板中断面表面宽度方向，在纵向残余应力表征上，耦合本构模型的模拟结果与X射线衍射测量结果具有较好的一致性，验证了耦合本构模型的正确性，并表明相变塑性对相变区的残余应力存在一定的松弛作用；对于装甲钢近缝区纵向残余应力大小：完全相变区<部分相变区<未发生相变区。

兵器科学与技术； 装甲钢； 耦合本构模型； 有限元； 焊接残余应力； 组织

0 引言

装甲钢是一种用于作战装备的保护性合金材料，焊接是装甲钢结构的主要连接方式。由于熔焊时焊接热输入集中性，造成焊缝及热影响区附近高温度梯度，必然会导致焊缝附近冶金组织大梯度，这样焊缝和热影响区有较大的热应力及组织应力；应力作用下的相变，存在相变诱导塑性现象，即所施加的应力小于弱项的屈服强度，在相变过程中仍然会发生较大的塑性变形。由于合金元素的添加，增大了装甲钢过冷奥氏体在铁素体、珠光体转变区的稳定性，装甲钢过冷奥氏体在较低温度下发生相变，大量的研究和实验证明低温相变对焊接残余应力的演变和最终分布具有显著影响[1]。残余应力的大小和分布状态对焊接结构的脆性破坏、疲劳破坏、应力腐蚀开裂以及其他各种破坏都有显著的影响。采用实验测定焊件表面及其内部的残余应力分布，不仅费时费力，增加成本，而且在实际的工程应用当中，还会受到一定的制约。

随着计算机软硬件技术的发展和非线性有限元理论的日臻完善，计算焊接力学已经建立[2]，并且在模拟复杂的焊接现象中发挥越来越大的作用。为了准确预测装甲钢焊接接头及热影响区的残余应力分布，需要在传统热弹塑性有限元分析的基础上考虑固态组织转变的影响，即从温度- 组织- 应力三者耦合的角度对装甲钢焊接过程进行分析。Oddy等对焊接应变场进行了有限元分析，在总应变率中计入了相变应变率[3-4]。Leblond等就相变对低合金钢塑性行为的影响进了研究，采用理论与数值模拟相结合，导出了一系列基本关系式[5-8]，并在此基础上发展了SYSWELD软件，该模型在近年来数值模拟研究中得到广泛的应用。Inoue等研究伴有相变的温度变化过程中，温度、相变、热应力三者之间的耦合效应，并提出了在考虑耦合效应的条件下本构方程的一般形式，并且开发出数值模拟软件HEARTS[9]。Ronda等用统一的方法推导了相变规律和相变塑性，建立了相容的TMM模型，并形成了系统理论[10]。国内对此的研究工作开展的较少，刘俊龑等以FEPG软件作为开发平台，针对9Cr1Mo钢Satoh实验，采用相变动力学考虑马氏体组织转变，将相变诱导塑性应变增量引入到总应变增量的分解式中，考虑相变过程对残余应力的影响[11]；根据所建立的温度- 组织- 应力耦合模型，针对9Cr1Mo钢管道环焊进行了数值模拟，当考虑固态相变对焊接残余应力得影响时，三维有限元计算的结果均与实际测量结果吻合的较好[12]。邓德安等基于JWRIAN焊接数值模拟软件，开发了考虑固态相变的热- 冶金- 力学耦合的数值计算方法来模拟低温相变钢的焊接残余应力，结果表明，相变引起的体积变化和屈服强度变化对最终的焊接残余应力分布和大小有显著影响，相变塑性与前二者相比较影响相对较小[13]；基于SYSWELD软件开发了考虑材料固态相变的热- 冶金- 力学耦合的有限元计算方法，探讨了固态相变引起的体积变化、屈服强度变化和相变塑性对焊接残余应力形成过程及最终残余应力分布的影响[14]。Ma等采用迭代子结构法和JWRIAN软件研究了U71Mn钢轨闪光对接焊残余应力，数值模拟结果和实验结果表明固态相变对焊接残余应力的形成有重要影响[15]。

本文针对某装甲钢CO2气体保护焊(MAG)焊接过程进行研究，根据传热学、固态相变理论和连续介质力学，建立温度- 组织- 应力耦合的本构模型，本构模型中综合考虑了固态相变引起的体积变化、力学性能变化和相变塑性。通过二次开发将该本构模型嵌入通用有限元软件中，并对装甲钢平板对接焊进行了研究；获得了装甲钢焊接热循环过程中温度、组织及残余应力变化规律，重点研究了相变塑性对纵向残余应力的影响。

1 多场耦合宏观唯象模型

采用多场耦合宏观唯象模型对装甲钢焊接进行研究。该宏观唯象模型采用传热、相变和变形这3类基本方程来构建基本的理论模型框架，且在这些基本方程中引入相互的耦合项，以体现基本物理过程之间的耦合作用。图1为焊接过程中多物理场耦合关系示意图。

图1 多物理场耦合关系示意图Fig.1 Schematic diagram of multi-physical fields coupling

从图1中可以看出，各物理场耦合关系如下：温度场对应力的影响表现为产生热应力；应力对温度场的影响：淬火、焊接等热加工过程，考虑到工件的实际变形量不超过2%～3%，塑性功耗散可忽略不计；组织转变对温度场的影响：由于相变产生组织的热焓值不同，相变过程伴随潜热的释放与吸收进而影响温度场；温度对组织转变的作用：温度是影响相变开始和过程的主要因素；组织转变对应力的影响：在相变过程中，各组成相的比容差异将造成相变应力以及应力作用下相变过程产生的相变塑性应变，同时由于材料的绝大多数参数除了依赖于温度，实际上也依赖于相态，因此，相变也会对引起材料参数的变化，进而影响材料的力学行为。图1中实线代表在本文中考虑的耦合效应，虚线代表其耦合效应在本文中未考虑。

由于一般有限元软件没有能够实现上述耦合的求解策略，本文根据温度场、组织场及应力应变场耦合的原理提出了考虑耦合效应条件下本构方程的一般形式，利用用户子程序UMAT对ABAQUS商用有限元软件进行了二次开发，构建了焊接过程多物理场耦合数值模拟平台。

2 装甲钢平板对接焊研究

焊件为600 mm×200 mm×5 mm装甲钢板。坡口型式为Y型坡口，坡口角度为90°，钝边高度为2 mm，焊缝根部间隙为1 mm. 焊接工艺为MAG，焊接工艺参数：电弧电压U=25 V，焊接电流I=210 A，焊接速度v=5 mm/s. 填充材料为奥氏体不锈钢焊丝。为了节省计算时间和提高计算精度，在温度梯度大的焊缝及热影响区域采用较密网格，而离焊缝较远、温度梯度小的区域采用粗大网格。

2.1 温度场求解

在温度场求解中，本文考虑材料热物性随温度变化，忽略相变潜热、塑性耗散对温度场的影响。在加热过程中，相对于焊接热源输入，固态相变潜热可以忽略。在冷却过程中，过冷奥氏体向马氏体转变，释放的固态相变潜热降低了相变区的冷却速度，对温度场的计算结果有一定的影响，固态相变潜热的影响在下一步的工作中进行完善。根据Fourier定律和能量守恒定律，获得焊件内热传导方程如(1)式所示：

(1)

结合焊接过程的初始条件和边界条件可获得焊接过程中焊件内部温度场。其中：采用移动热源来模拟焊接热输入，热源内热流的分布采用Gloadk等提出的双椭球分布[16]。采用牛顿冷却公式来考虑焊接外表面与空气的对流换热，采用Steffen-Boltzmann方程来考虑辐射换热。此外模型中考虑了融化凝固潜热效应。求解每一个增量步结束时焊件内各节点温度的平衡收敛值，并存储于数据文件，在组织场和应力应变场的求解中将温度场结果作为体载荷按照对应时间读入模型进行分析计算。

2.2 组织场求解

某装甲钢初始组织为回火索氏体组织。焊接热循环过程中，依赖于材料积分点在热循环过程中所经历的峰值温度，当峰值温度超过奥氏体化开始温度TAs，发生初始组织(体心立方晶格)向奥氏体组织(面心立方晶格)转变，由于奥氏体比容较大，材料发生收缩。在冷却过程中，当温度低于马氏体转变开始温度TMs，过冷奥氏体(面心立方晶格)向马氏体(体心四面体晶格)转变，材料体积膨胀。

2.2.1 奥氏体化动力学

加热时奥氏体的形成过程是一个形核和长大的过程。其奥氏体化过程可简单地分为：奥氏体晶核形成、奥氏体晶核长大、残余渗碳体溶解以及奥氏体成分均匀化。对于连续加热过程的奥氏体化计算，有杠杆法、基于Johnson-Mehl-Avrami模型方法和INOUE奥氏体化相变动力学模型[17]。INOUE奥氏体化相变动力学模型是介于前二者之间的一种模型，如(2)式所示。本文采用此奥氏体化相变动力学模型。

(2)

式中：fA为奥氏体体积分数；TAf为奥氏体化结束温度；CA和CD为与材料相关的系数。

2.2.2 过冷奥氏体非扩散型相变

过冷奥氏体向马氏体转变也是一个形核和长大的过程，只是由于马氏体形成速度极快，瞬间形核，瞬间长大。转变过程中铁和碳原子都不发生扩散。马氏体的转变量仅取决于温度，与时间无关。当温度低于马氏体转变温度TMs，过冷奥氏体开始向马氏体转变；当温度低于马氏体转变终了温度TMf时，马氏体转变结束。马氏体的转变量可以用Koistinen-Marburger公式计算[18]：

fM=1-exp (-CC(TMs-T)),

(3)

式中：fM为马氏体体积分数；CC为随化学成分而变的常数，它反映了马氏体的转变速率。

孙朝阳对某型号装甲钢马氏体转变进行了实验研究，采用Koistinen-Marburger公式对实验数据进行回归，得到CC值为0.028[19]，不同于一般高碳合金钢的值0.011，可见钢中碳含量对CC的影响很大。

组织转变具体实现步骤如图2所示。

图2 组织转变程序流程图Fig.2 Flowchart of microstructure transformation process

2.3 应力应变场求解

2.3.1 材料力学性能的确定

1) 单相力学性能。对于每一相的力学性能有如下假定：每一相的力学性能依赖于温度，如杨氏模量、屈服强度、塑性模量和线弹性系数等；材料的弹性区符合广义胡克定律；塑性区符合Mises屈服准则、关联流动法则和等向硬化准则。模拟所用到的各相力学性能参数参考文献[19]中通过对装甲钢物理模拟所得到的数据。由于文献[19]所给的数据为淬火过程数值模拟，温度范围有限，在焊接过程数值模拟中，本文对高温相(奥氏体组织)材料性能做了一定的外推。

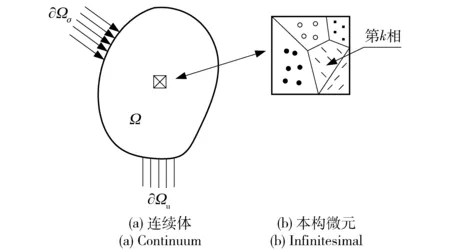
图3 多相材料的局部- 均匀化处理示意图Fig.3 Schematic diagram of local homogenization of multi-phase material

2)多相混合力学性能。由于焊接过程中工件内各点温度进程不同，各点的相变可能不同步。对于图3(a)所示的这种具有力和位移边界多相混合非均匀连续体的行为，其中Ω为求解域，∂Ωσ为力边界条件，∂Ωu为位移边界条件。本文模型中采用局部- 均匀化的方法从微观- 宏观两个尺度加以描述，即首先通过局部化处理，从微观角度对材料中的单一组织的行为进行描述。在此基础上，利用均匀化的方法实现对材料宏观力学行为的表征，图3(b)为多相混合非均匀连续体一本构微元。利用该方法，实现了在对材料宏观行为的描述中考虑到每一个组成相自身力学行为特点[20]。此时材料宏观力学性能不仅依赖于温度且随相变变化，采用混合法则来求解材料宏观力学性能。

(4)

2.3.2 温度- 组织- 应力本构方程的建立及数值实现

综合考虑温度场、应力应变场及组织场相互耦合关系，首先根据连续介质力学，将总的应变率可加性分解为弹性应变率张量、经典塑性应变率张量、热应变率张量、相变应变率张量和相变诱导塑性应变率张量。相对于传统的热弹塑性本构方程多出两项，即相变应变率张量和相变诱导塑性应变率张量。

(5)

弹性应变率和热应变率可以采用广义胡克定律和线膨胀定理分别定义。对于经典塑性应变率采用等塑性应变的假设[8]，即认为在组成相中的平均微观塑性应变与多相混合材料的宏观塑性应变相等。

相变应变率张量可表示为

(6)

相变塑性是在组织转变过程中施加外力小于弱项的弹性极限而观察到的一种不可逆塑性变形。通常有两种机理被提出用来解释相变塑性：Magee机理和Greenwood-Johnson机理。对于外加载荷(应力)较小的情况，现有相变塑性的模型都是基于Greenwood-Johnson的机理来进行的，Magee效应可以忽略。对于焊接和热处理过程，应力水平较低，本文采用Greenwood-Johnson机理。

相变塑性应变率张量可表示为

(7)

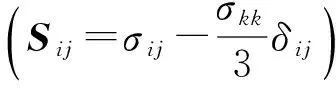
根据g(fk)的不同，有表1所列的3种模型。

表1 相变塑性演化函数Tab.1 Evolution functions of transformation induced plasticity

由于Desalos模型形式简单，并可扩展到多轴应力状态，本文采用了此模型。

采用向后欧拉法对率本构方程进行积分，将率本构方程变换为增量本构方程。

在弹性区域内，应变增量可以表示为

(8)

在塑性区域内，应变增量可以表示为

(9)

图4为多物理场耦合弹塑性增量本构关系在材料子程序UMAT实现流程图。采用增量迭代的方法，每一个增量步的求解流程为：1)求解温度场，然后根据相变计算模块获得各相组织体积分数和其体积分数增量，结合物理模拟得到的各相力学性能，采用混合法则获得多相混合组织的力学性能；2)采用径向返回算法得到应力应变增量的计算，并计算得到Jacobian矩阵，完成迭代；3)将体积分数、各应变分量等作为状态变量存储，增量步结束。各种耦合关系的计算是通过对各参数矩阵和载荷向量的定制加以实现的，而非线性问题的解决，则充分利用了通用有限元软件的强大非线性迭代算法。

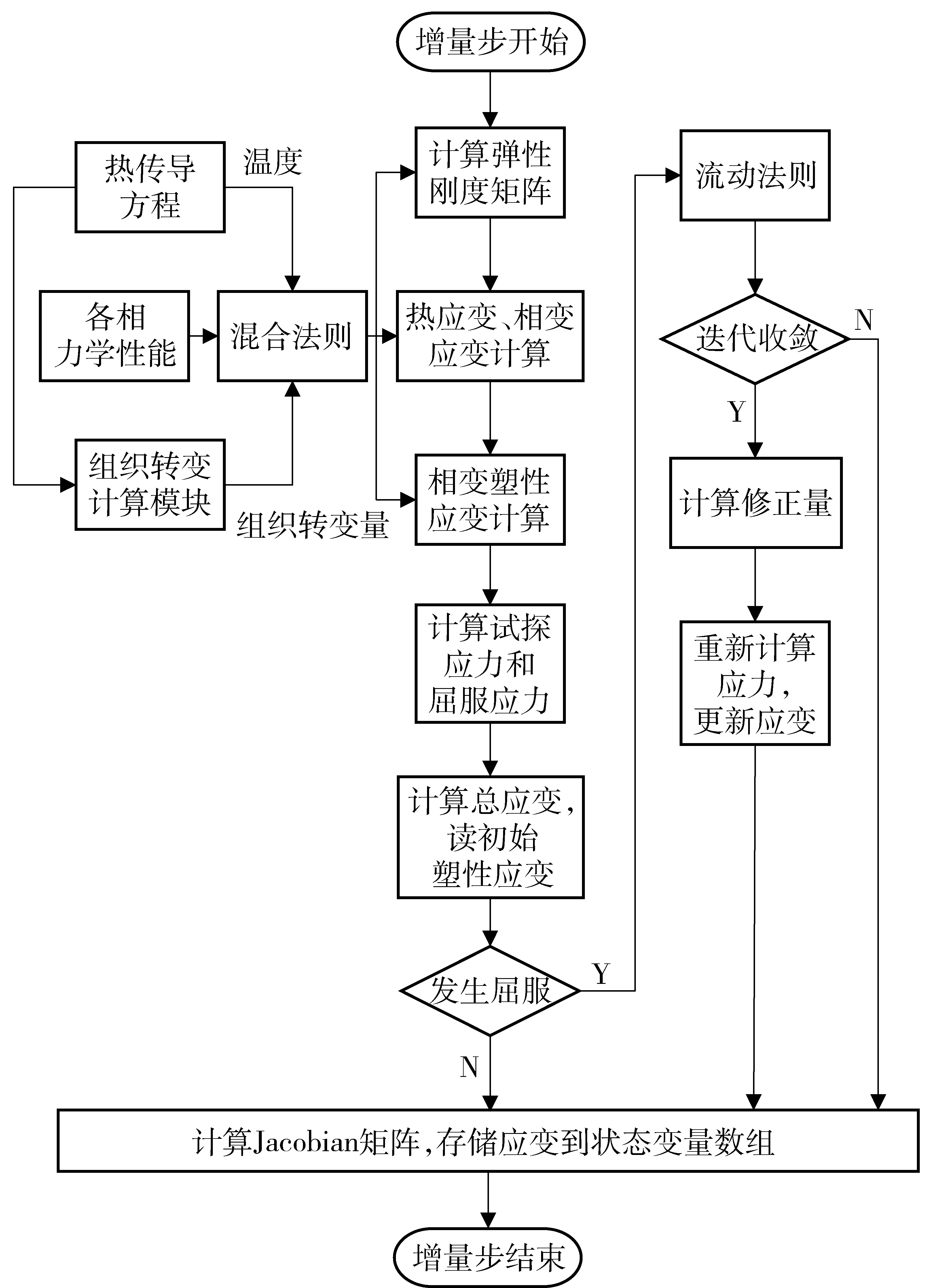
图4 多物理场耦合弹塑性增量本构关系的数值实现Fig.4 Numerical implementation of coupling elasto-plastic incremental constitutive relationship of multi-physical fields

3 数值计算结果验证与分析

3.1 温度场验证

装甲钢焊接温度场分布云图如图5所示，其符合典型弧焊温度场分布特征，前端温度梯度较大，后端温度梯度较小。采用K型热电偶测温的方法测量焊件上表面距离焊缝中心线10.5 mm、15.5 mm和20.5 mm 3个位置的焊接热循环，在有限元模型中取出对应这3个对应位置的热循环(对应A、B和C点)，计算值和实验测量值的比较如图6所示。从图6中可以看出, 不论是各点的峰值温度还是温度曲线都与实验结果比较吻合，二者在温度数值上稍有误差。温度场计算结果为组织场和应力应变场的计算提供了输入。

图5 装甲钢焊接温度场云图Fig.5 Contour of welding temperature field of armour steel

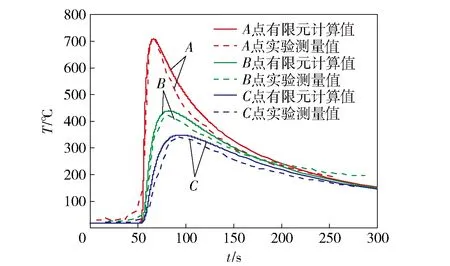
图6 焊接温度计算值和实验值比较Fig.6 Comparison of simulated and experimental results of welding temperatures

3.2 残余应力场验证

图7为焊后装甲钢中断面上纵向残余应力σz分布云图，图8为焊后装甲钢中断面上表面宽度方向考虑相变塑性、未考虑相变塑性和X射线衍射测量的纵向残余应力对比。由此可见，在焊缝和热影响区，耦合本构模型分析结果与X射线衍射测试结果吻合较好，而远离焊缝和热影响区，具有一定的差异，原因为耦合本构模型分析没有考虑装甲钢平板焊接前各种加工制造产生的残余应力。从图8中可以看出是否考虑相变塑性对纵向残余应力有显著影响，考虑相变塑性时，纵向残余应力绝对值要小于未考虑相变塑性的纵向残余应力的绝对值，也就是相变塑性在一定程度上降低了纵向残余应力，这与文献[23-24]结论一致。

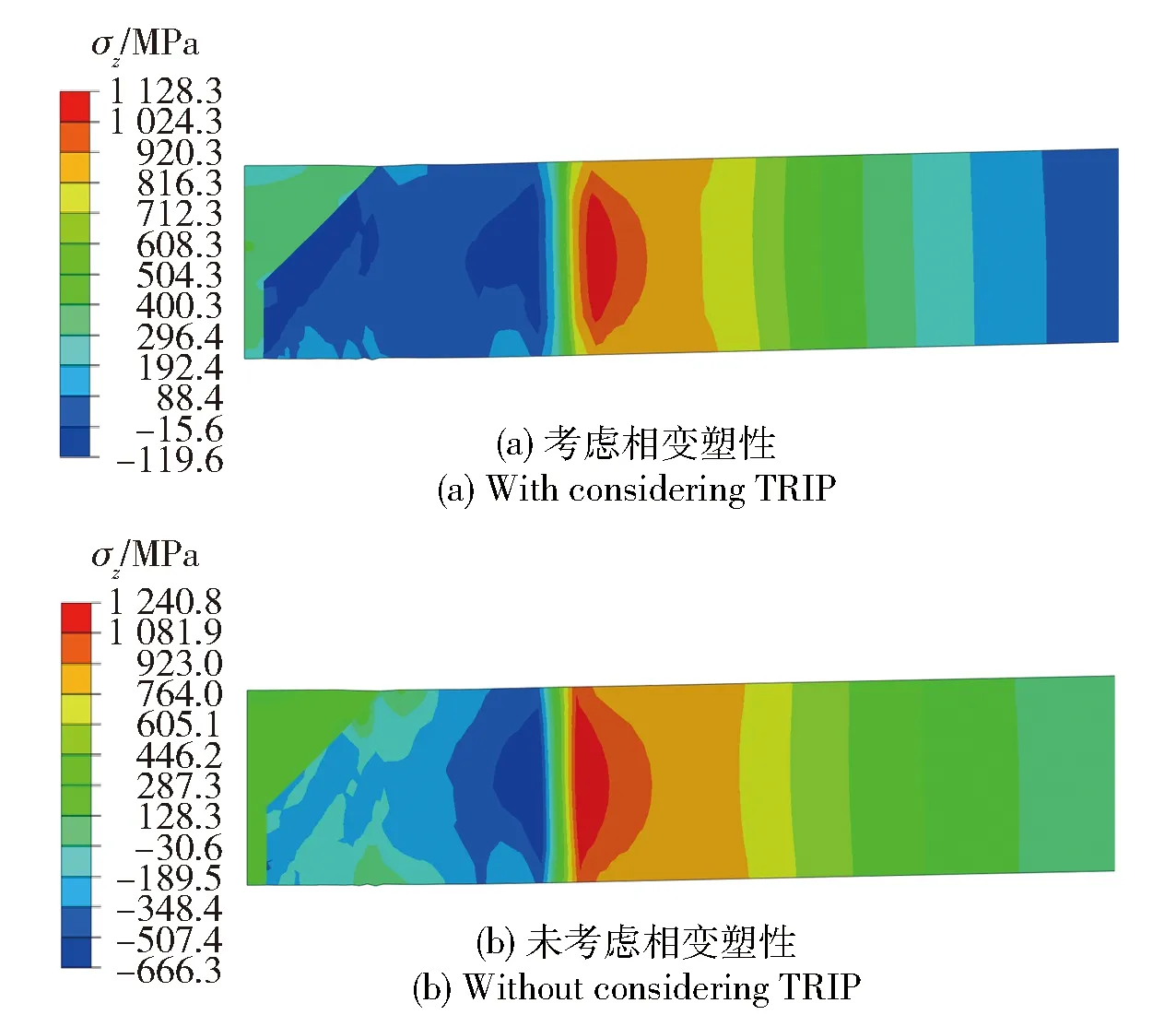
图7 装甲钢中断面纵向残余应力分布云图Fig.7 Contours of longitudinal residual stresses of armour steel across mid-section

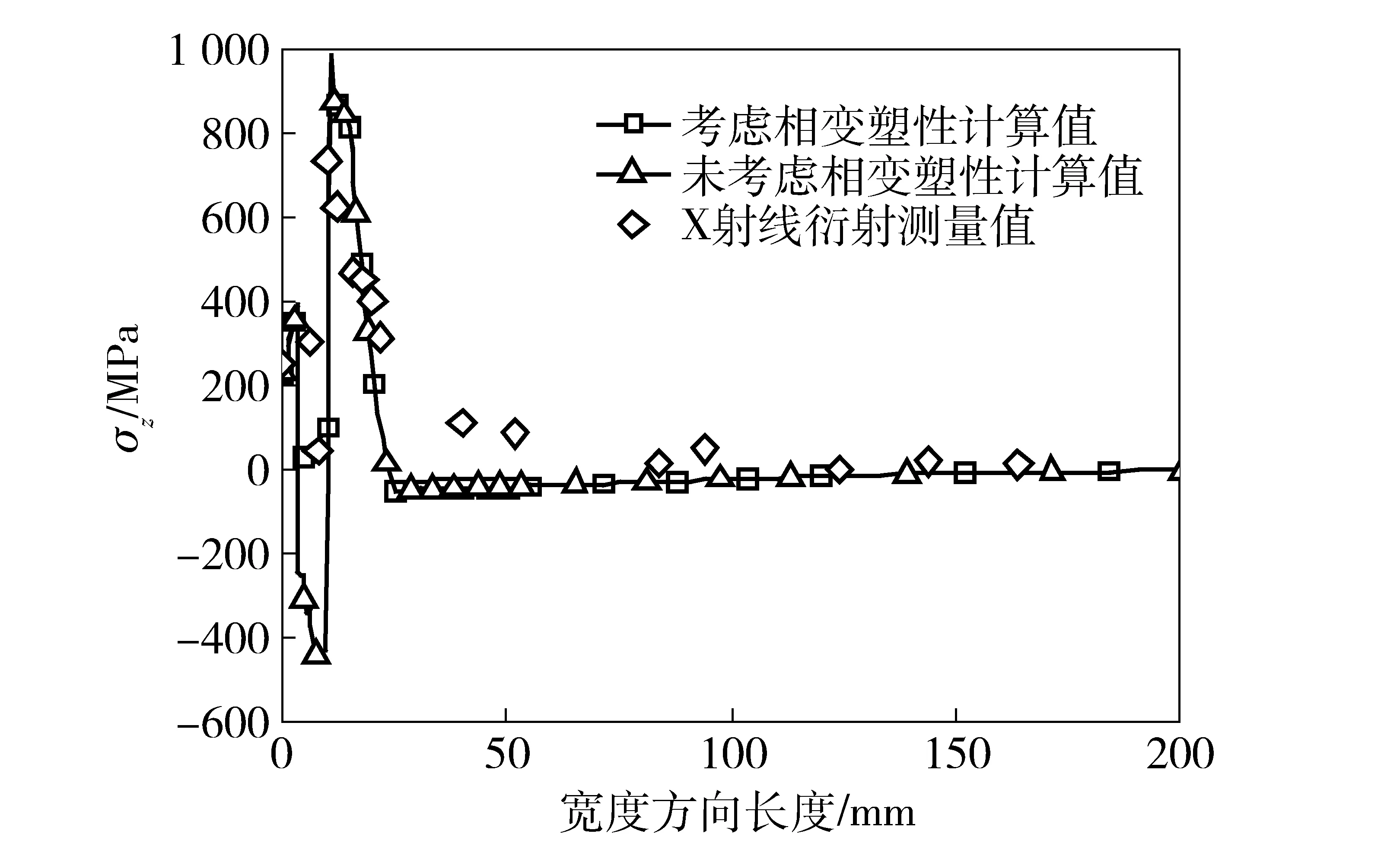
图8 装甲钢平板表面宽度方向纵向残余应力Fig.8 Longitudinal residual stresses along width direction on the upper surface of armour steel plate

3.3 残余应力场分析

从图8还可以看出，纵向残余应力分布呈双峰分布，一个峰值在奥氏体焊丝填充的焊缝处，另一个峰值在近缝区，且近缝区有很高的残余拉应力，两个峰值之间纵向残余应力值很小。奥氏体焊丝在热循环过程中不发生组织转变，其纵向残余应力为拉应力状态。由于奥氏体焊丝较母材承受塑性变形能力强，焊接过程中产生的塑性变形基本上由奥氏体焊丝承担，因此奥氏体焊丝加工硬化现象明显，在数值模拟中同时考虑了奥氏体的加工硬化，所以其纵向残余应力值超过了奥氏体焊丝常温时的屈服极限(278 MPa)。

取装甲钢平板上表面距焊缝中心线7.75 mm处一点，称为P1点。从图9可以看出，由于P1点热循环峰值温度大于TAf，f表示相体积分数，其值介于0和1之间。焊接热循环加热过程中，初始组织完全转变为奥氏体组织，随后冷却过程中，奥氏体完全转变为马氏体。最后为均一的马氏体组织。

图9 P1点焊接热循环过程中各相体积分数随温度变化Fig.9 Evolution of volume fraction of each phase with temperature at P1 point during welding thermal cycle

取P1点纵向残余应力在整个焊接热循环过程中演变，如图10所示。从图10可以看出，当热源接近，焊缝附近金属受热膨胀，由于受到周围金属的约束，产生压缩应力，压缩应力随着温度升高而增加。当温度进一步升高，由于初始屈服极限的降低，P1点将发生塑性变形，且屈服极限随温度的升高而降低，所以纵向残余应力绝对值随温度增加变小。当温度升高到初始组织向奥氏体组织转变温度，由于奥氏体比容相对于初始组织小，试样将发生体积收缩，由于整体约束作用，P1点应力转向为拉应力。当初始组织向奥氏体组织转变结束，温度继续升高，由于热膨胀，该点又为压应力状态，由于此时材料处于高温，屈服强度很低，压应力绝对值很小。随着热源的离去，P1点温度降低，由于热收缩作用，P1点为拉伸应力状态，且随着温度的降低逐渐增加，一直到奥氏体组织向马氏体组织转变温度开始，由于马氏体组织比容较奥氏体组织大，试样将发生体积膨胀。这样应力状态将由拉应力向压应力转变，当奥氏体向马氏体转变结束，随着温度继续降低，由于热收缩，压应力绝对值又减小。这也解释了完全奥氏体化区域最终纵向残余应力绝对值较小的原因。

图10 P1点焊接热循环过程中纵向残余应力演变Fig.10 Evolution of longitudinal residual stresses with temperature at P1 point during welding thermal cycle

取装甲钢平板上表面距焊缝中心线10.25 mm处一点，称为P2点。从图11可以看出，由于P2点峰值温度位于奥氏体化温度区间，焊接热循环加热过程中初始组织没有完全转变为奥氏体组织。随后冷却过程中，奥氏体完全转变为马氏体。最后的组织为初始组织和马氏体组织两相混合物。

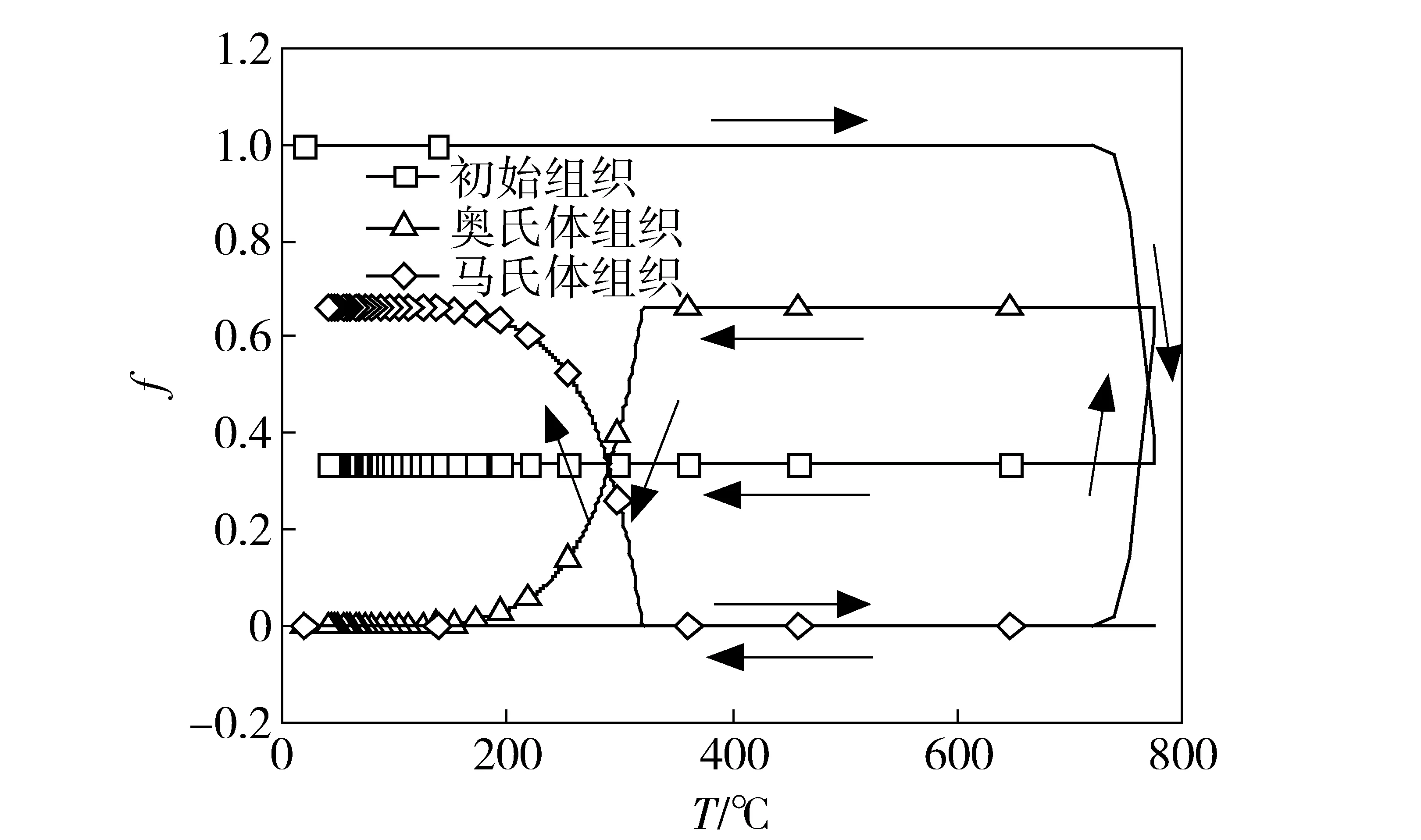
图11 P2点焊接热循环过程中各相体积分数随温度变化Fig.11 Evolution of volume fraction of each phase with temperature at P2 point during welding thermal cycle

图12为P2点纵向残余应力随温度的演变。纵向残余应力演变类似于图 10中完全奥氏体化区域纵向残余向应力随温度的演变，且部分奥氏体化区域最终残余应力大小高于完全奥氏体化区域的纵向残余应力。

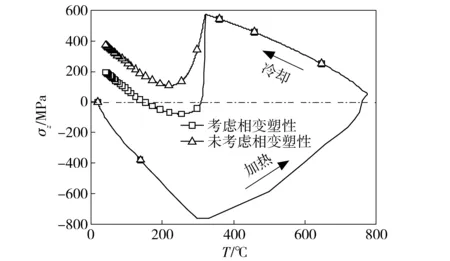
图12 P2点焊接热循环过程中纵向残余应力演变Fig.12 Evolution of longitudinal residual stresses with temperature at P2 point during welding thermal cycle

取装甲钢平板上表面距焊缝中心线11.75 mm处一点，称为P3点。从图13可以看出，由于P3点峰值温度小于TAs，焊接热循环加热过程中初始组织没有转变为奥氏体组织。随后冷却过程中，没有发生奥氏体向马氏体转变。最后为均一的初始组织。

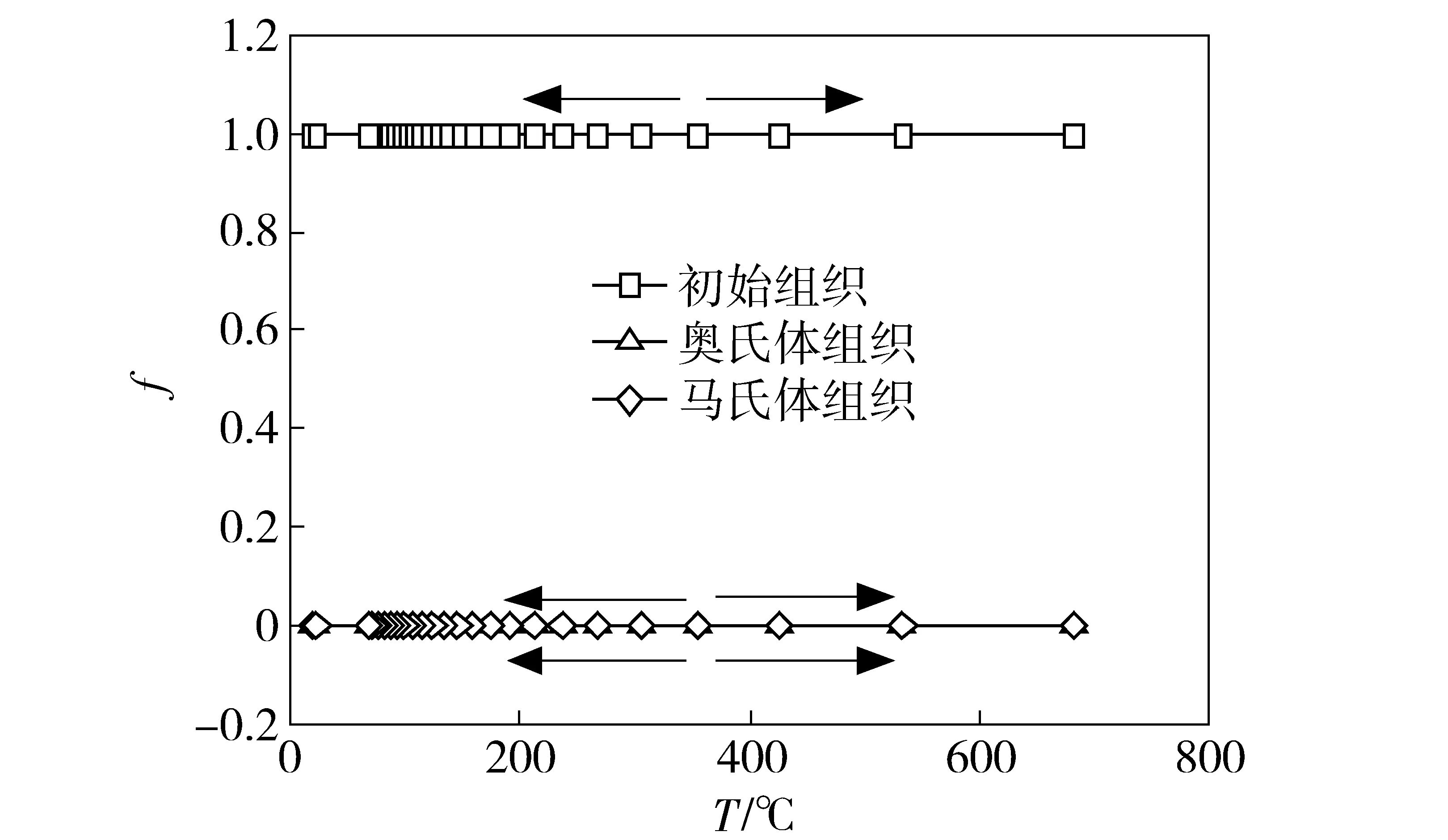
图13 P3点焊接热循环过程中各相体积分数随温度变化Fig.13 Evolution of volume fraction of each phase with temperature at P3 point during welding thermal cycle

图14为P3点纵向残余应力随温度的演变。整个焊接热循环过程未发生组织转变，且该点经受的峰值温度较高，所以最终的纵向残余应力较大，这也解释了近缝区出现较高纵向残余应力峰值的原因。随着距焊缝中心线距离的增加，焊接热循环过程中峰值温度的降低，纵向残余应力逐渐减小。

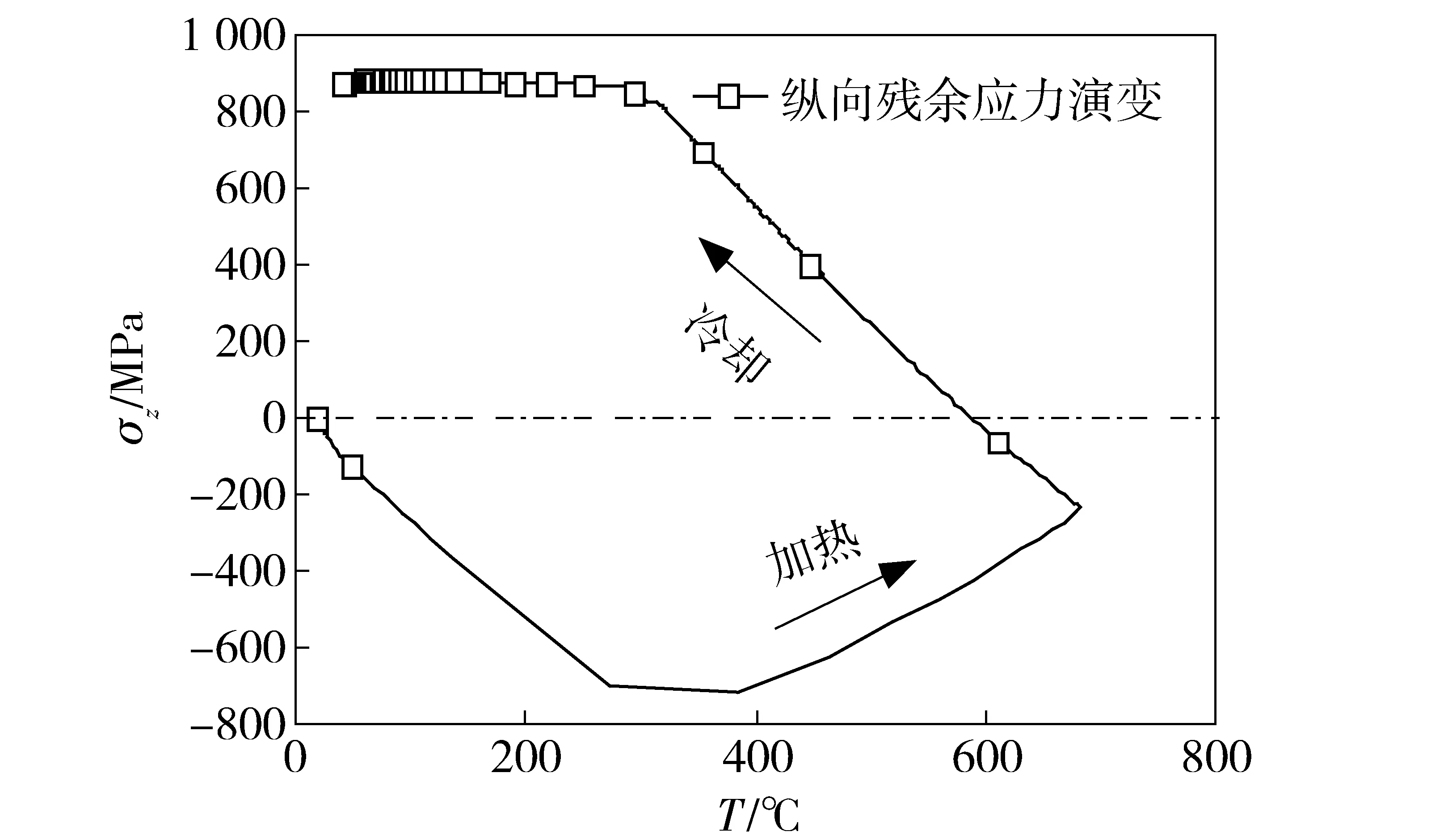
图14 P3点焊接热循环过程中纵向残余应力演变Fig.14 Evolution of longitudinal residual stresses with temperature at P3 point during welding thermal cycle

4 结论

1)在纵向残余应力表征上，温度- 组织- 应力耦合本构模型的有限元分析结果与X射线衍射测量结果具有较好的一致性，验证了所建立耦合本构模型的正确性。

2)相变塑性对相变区残余应力有一定的松弛作用，也就是在一定程度上降低了残余应力的水平。纵向残余应力在完全相变区考虑相变塑性降低了460 MPa，在不完全相变区降低了170 MPa. 相变塑性对残余应力的演变和最终大小的影响不可忽视。

3)在装甲钢平板中断面上表面宽度方向，纵向残余应力分布呈双峰分布。奥氏体焊丝填充的焊缝处峰值产生的原因为：奥氏体焊丝在热循环过程中不发生组织转变，且焊接过程中产生的塑性变形基本上由奥氏体焊丝承担，同时数值模拟中考虑了奥气体焊丝的加工硬化，该处的纵向残余应力值超过了奥氏体焊丝常温时的屈服极限。

4)近缝区峰值产生的原因为：马氏体相变引起的3个因素变化对纵向残余应力影响，体积膨胀降低拉应力的水平、屈服强度增加提高了应力水平及相变塑性对残余应力水平的降低。三者同时作用，完全相变区体积膨胀大，纵向残余应力由拉应力转变为压应力状态，加上相变塑性进一步降低应力水平。部分相变区分析同上。未发生相变区只有热循环导致的残余拉应力，由于装甲钢屈服强度较高，故其应力较大。对于装甲钢近缝区纵向残余应力大小：完全相变区<部分相变区<未发生相变区。

References)

[1] Deng D A, Tong Y G, Ma N, et al． Prediction of the residual welding stress in 2.25Cr-1Mo steel by taking into account the effect of solid-state phase transformation[J]. Acta Metallurgica Sinica: English Letters, 2013, 26(3): 333-339.

[2] Lindgren L E．Computational welding mechanics[M]. London: Woodhead Publishing, 2007.

[3] Oddy A S, McDill J M J, Goldak J A. Consistent strain fields in 3D finite element analysis of welds[J]. Journal of Pressure Vessel Technology, 1990, 112(8): 309-311.

[4] Oddy A S, Goldak J A, McDill J M J. Numerical analysis of transformation plasticity in 3D finite element analysis of welds[J]. European Journal of Mechanics, A/Solids, 1990, 9(3): 253-263.

[5] Leblond J B, Mottet G, Devaux J C. A theoretical and numerical approach to the plastic behaviour of steels during phase transformations—I. Derivation of general relations[J]. Journal of the Mechanics & Physics of Solids, 1986, 34(4):395-409.

[6] Leblond J B, Mottet G, Devaux J C. A theoretical and numerical approach to the plastic behavior of steels during phase transformations, II. Study of classical plasticity for ideal-plastic phases[J]. Journal of the Mechanics & Physics of Solids, 1986, 34(4): 411-432.

[7] Leblond J B, Devaux J, Devaux J C. Mathematical modeling of transformation plasticity in steels, I: case of ideal-plastic phases[J]. International Journal of Plasticity, 1989, 5(6): 511-572.

[8] Leblond, J B. Mathematical modeling of transformation plasticity in steels II: coupling with strain hardening phenomena[J]. International Journal of Plasticity, 1989, 5(6): 573-591.

[9] Inoue T, Wang Z G. Coupling between stress, temperature, and metallic structures during processes involving phase transformations[J]. Materials Science and Technology, 1984, 1(10): 845-850.

[10] Ronda J, Oliver G J. Consistent thermo-mechano-metallurgical model of welded steel with unified approach to derivation of phase evolution laws and transformation-induced plasticity[J].Computer Methods in Applied Mechanics and Engineering, 2000, 189(2): 361-417.

[11] 刘俊龑, 陆皓, 陈俊梅,等. 基于相变诱导塑性Satoh试验的有限元模拟[J]. 焊接学报, 2008, 29(3): 105-108. LIU Jun-yan, LU Hao, CHEN Jun-mei,et al.Finite element simulation of Satoh test taking into account transformation induced plasticity[J]. Transaction of The China Welding Institution, 2008, 29(3): 105-108.(in Chinese)

[12] 刘俊龑,陆皓,陈俊梅,等. 焊接残余应力的温度- 组织- 应力耦合分析[J]. 焊接学报, 2009, 30(2): 95-98. LIU Jun-yan, LU Hao, CHEN Jun-mei, et al.Thermal-mechano-metallurgical coupled analysis of welding residual stress[J]. Transaction of The China Welding Institution, 2009, 30(2): 95-98.(in Chinese)

[13] 邓德安,村川英一,麻宁绪. 相变塑性对低温相变钢焊接接头残余应力计算精度的影响[J]. 焊接学报,2014, 35(8): 9-12. DENG De-an, Murakawa Hidekazu, MA Ning-xu. Influence of TRIP on calculated results of residual stress in a low temperature transformation steel joint[J]. Transaction of The China Welding Institution, 2014, 35(8): 9-12.(in Chinese)

[14] 邓德安,张彦斌,李索,等. 固态相变对P92钢焊接接头残余应力的影响[J]. 金属学报, 2016, 52(4): 394-402. DENG De-an, ZHANG Yan-bin, LI Suo,et al．Influence of solid-state phase transformation on residual stress in P92 steel welded joint[J]. Acta Metallurgica Sinica, 2016, 52(4): 394-402. (in Chinese)

[15] Ma N, Cai Z, Huang H, et al. Investigation of welding residual stress in flash-butt joint of U71Mn rail steel by numerical simulation and experiment[J]. Materials & Design, 2015, 88:1296-1309.

[16] Goldak J, Chakravarti A, Bibby M. A new finite element model for welding heat sources[J]. Metallurgical and Materials Transactions B, 1984, 15(2):299-305.

[17] Inoue T, Arimoto K. Development and implementation of CAE system ‘HEARTS’ for heat treatment simulation based on metallo-thermo-mechanics[J]. Journal of Materials Engineering and Performance, 1997, 6(1): 51-60.

[18] Kosistinen D P, Marburger R E. A general equation prescribing extent of austenite-martensite transformation in pure Fe-C alloys and plain carbon steel[J]. Acta Metallurgica, 1959, 7(1): 59-60.

[19] 孙朝阳. 装甲钢马氏体相变本构行为研究及在淬火模拟中的应用[D].北京:清华大学, 2008:21-33. SU Chao-yang. Constitutive behavior of martensitic transformation forarmour steel and its applications in quench modeling[D]. Beijing: Tsinghua University, 2008:21-33.(in Chinese)

[20] Coret M, Combescure A. A mesomodel for the numerical simulation of the multiphasic behavior of materials under anisothermal loading (application to two low-carbon steels)[J]. International Journal of Mechanical Sciences, 2002, 44(9): 1947-1963.

[21] Denis S, Gautier E, Sjostrom S, et al. Influence of stresses on the kinetics of pearlitic transformation during continuous cooling[J]. Acta Metallurgica, 1987, 35(7): 1621-1632.

[22] Desalos Y, Giusti J, Gunsberg F. Deformations et contraintes lors du traitement termique de pieces enacier[R]. Saint-Germainen-Laye: Institut de Recherches de la Siderurgie Francaise, 1982.

[23] Borjesson L, Lindgren L E. Simulation of multipass welding with simultaneous computation of material properties[J]. Journal of Engineering Materials & Technology, 2001, 123(1):106-111.

[24] Vincent Y, Jullien J F, Gilles P. Thermo-mechanical consequences of phase transformations in the heat-affected zone using a cyclic uniaxial test[J]. International Journal of Solids & Structures, 2005, 42(14):4077-4098.

Establishment of Thermo-metallurgical-mechanical Coupling Constitutive Model for Armour Steel and Its Application in Welding Numerical Simulation

SUN Yu-jie， CUI Qing-chun， HAN Xuan-xuan， SHI Chun-ming

(Northwest Institute of Mechanical & Electrical Engineering, Xianyang 712099, Shaanxi, China)

Solid-state phase transformation has significant effect on the evolution and magnitude of welding residual stress for armour steel during welding thermal cycle, while the current constitutive model can not take solid-state phase transformation into account. Based on heat transfer theory, solid-state phase transformation theory and continuum mechanics, a thermo-metallurgical-mechanical coupling constitutive model in which the effects of volumetric change, yield strength change and transformation induced plasticity(TRIP) on residual stresses due to solid-state phase transformation on welding residual stress are considered is established. The constitutive model is inserted into a general purpose implicit finite element program via user material subroutine UMAT. The change rules of temperature, microstructure and residual stresses are obtained for a butt welding of armour steel plates. The research results show that longitudinal residual stresses obtained from the coupling constitutive model are in good agreement with experimental results measured by X-ray diffraction perpendicular to weld centerline on the upper surface of the weldment. The correctness of developed computational method is confirmed, and TRIP has certain effects on the evolution of longitudinal residual stresses. For the magnitude of longitudinal residual stresses in the vicinity of weld zone, the fully-transformed region is less than partially-transformed region, and the partially-transformed region is less than untransformed region.

ordnance science and technology; armour steel; coupling constitute model; finite element method; welding residual stresses; microstructure

2016-05-17

孙玉杰(1981—)，男，高级工程师。E-mail:sunyujiegood@eyou.com

TG404

A

1000-1093(2017)03-0540-09

10.3969/j.issn.1000-1093.2017.03.017