基于快速抛光技术的光学元件材料去除模型研究
2017-04-11林涛杨炜王健
林涛, 杨炜, 王健
(1.厦门大学 航空航天学院, 福建 厦门 361005; 2.中国工程物理研究院 激光聚变研究中心, 四川 绵阳 621900)
基于快速抛光技术的光学元件材料去除模型研究
林涛1, 杨炜1, 王健2
(1.厦门大学 航空航天学院, 福建 厦门 361005; 2.中国工程物理研究院 激光聚变研究中心, 四川 绵阳 621900)
为精确控制抛光阶段材料去除,实现光学元件的确定性抛光加工,在分析快速抛光原理和快速抛光材料去除机制基础上,从单颗磨粒受力和抛光垫峰点捕获的磨粒数出发,获得量化的单颗磨粒瞬时切除体积和抛光接触区参与有效磨粒数,从而建立一种光学元件快速抛光材料去除模型。研究结果表明:以材料去除量为实验对象,在不同抛光液、抛光垫和光学元件实验条件下,材料去除模型的理论预测结果与实验结果较为吻合,材料去除量误差可以控制在9%以内。验证了该模型对于光学元件快速抛光技术的适用性,从而可以确定性的控制快速抛光时间和效率。
机械制造工艺与设备; 光学元件; 快速抛光; 材料去除模型
0 引言
针对激光核聚变研究,我国相关部门已建成神光Ⅰ、神光Ⅱ高功率激光装置,现在进行的神光Ⅲ装置的建设和研究更是一项庞大而又复杂的巨型工程,其中使用了大量的光学元件,光学元件超精密加工表面质量控制问题已经成为惯性约束聚变研究中重点关注的问题,直接影响着强激光系统的使用性能[1-3]。目前,我国高精密光学元件加工水平和世界上技术先进国家相比还有一定的差距,提高光学元件高效批量化加工,是摆在我国光学制造领域的一个重要课题。
传统平面光学元件在抛光加工过程中,需要经过粗抛、环形抛光和精抛才能提高元件表面面型精度,降低表面粗糙度和亚表面缺陷[4],整个抛光流程耗时长,不能满足大型光学工程的需求。快速抛光技术以其相对较高的材料去除率,已经全面取代了初抛,部分取代了环形抛光。因此,研究快速抛光技术的材料去除机制和模型,实现确定性的抛光技术尤为重要。
国内外学者对抛光技术的材料去除机制已经开展了广泛的研究,近年来也提出了一些相应的材料去除模型。例如:Luo等[5]基于磨粒磨损机制,针对硅片化学机械抛光(CMP)提出了材料微观去除模型,并建立了材料去除公式;Runnels等[6]提出了流体润滑模型,采用流体动力学方程建立了芯片表面抛光液流动模型;Christopher等[7]基于化学作用机制,应用化学动力学理论,提出抛光过程中的五步去除机制;Zhao等[8]基于原子/分子去除机制,认为抛光是表面的最外层原子或分子不断氧化和磨损的动态平衡过程。目前材料去除机理和去除模型的研究非常多而深入,几乎没有一个模型具有普遍适用性,但不同的运用场合可以有改进和补充的空间。
本文从磨粒磨损机制出发,建立一种光学元件快速抛光材料去除模型,验证了在不同类型光学元件、不同类型抛光垫和不同类型抛光液条件下,模型能够适应光学元件的快速抛光,实现确定性抛光技术,材料去除误差可以控制在合理的范围之内。
1 光学元件快速抛光技术
1.1 快速抛光原理及材料去除机制
快速抛光原理如图1所示,将光学元件置于运动控制轴下端,将抛光垫贴在旋转抛光盘上;元件在运动控制轴的控制下可以独立旋转,运动控制轴可以上下移动,以此对元件施加不同的压力;抛光液通过喷管喷射到抛光垫表面,并通过抛光盘的旋转均匀散布到元件和抛光垫表面;元件相对于抛光垫运动,在机械磨削与化学侵蚀两种材料去除机制的交互作用下完成快速抛光加工。传统环形抛光只是靠元件重力,且元件是被动运动,快速抛光与初抛和环形抛光的区别之处在于有了加压装置,而且元件是主动运动,元件具有运动的独立性和快速性,且外界可对元件施加较大的压力[9]。
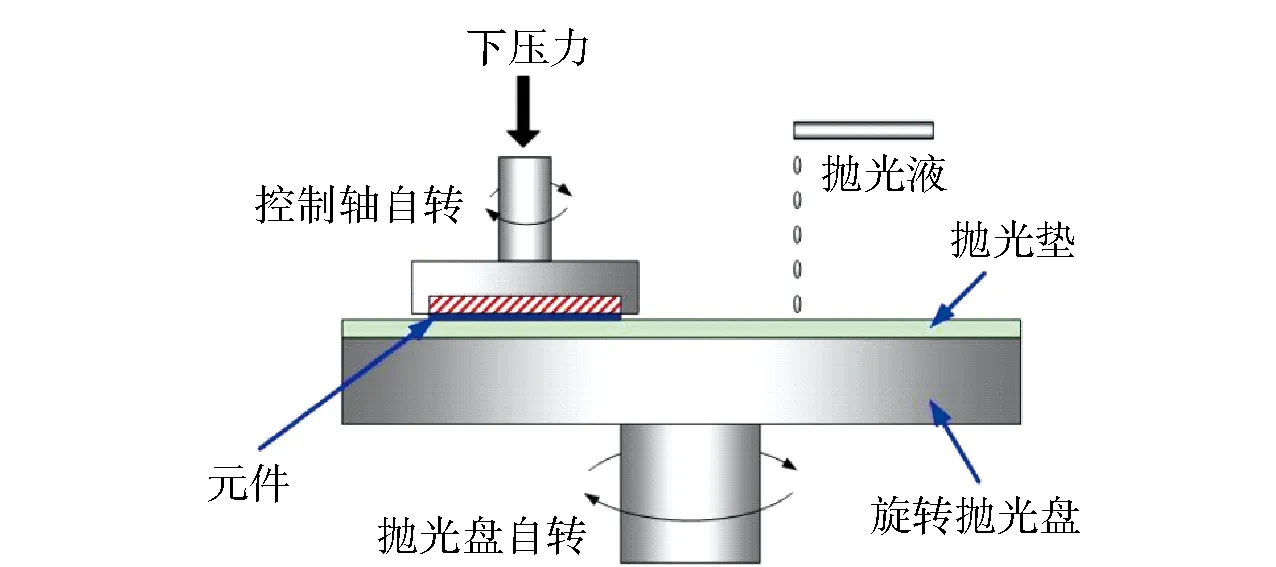
图1 快速抛光原理Fig.1 Fast polishing principle
对于快速抛光材料去除机制的研究首先要关注光学元件和抛光垫的接触状态。在抛光加工过程中,根据抛光盘和元件的接触状态及抛光液的润滑状态,元件和抛光盘之间的接触状态主要有3种:完全接触状态、部分接触状态、不接触状态 (流体润滑状态)。根据上述3种接触状态,可以将材料去除机理主要扩展为4种:磨粒磨损机制、流体润滑机制、原子/分子去除机制和化学作用机制。光学元件快速抛光技术一个显著特点就是拥有较高的材料去除率,其是基于较大的加工压力和较大的相对速度来实现的,光学元件和抛光垫的接触属于完全接触[10-11]。据此,快速抛光与CMP不同之处在于CMP更多考虑了化学因素,而在光学元件的快速抛光过程中,基于磨粒磨损机制的机械磨削作用在材料去除中占据主导地位,流体润滑和化学作用相对较小。
1.2 快速抛光材料去除模型
Luo等[5]基于磨粒磨损机制,认为元件和抛光垫直接接触且达到稳定接触状态,并进一步研究元件和抛光垫的实际接触面积、单颗参与去除材料有效磨粒受力、材料去除的有效磨粒数和单颗有效磨粒切除体积等因素,提出建立抛光材料去除模型所需3个前提条件:规律性分布的抛光垫表面峰点,抛光颗粒粒度正态分布,抛光颗粒、元件、抛光垫之间的塑性形变。通过对这3个前提条件验证,从而建立抛光材料去除模型[5,12]:
(1)
式中:MRR是材料去除量;ρw是元件的密度;ΔV是单颗有效磨粒瞬时切除体积;N是接触区内有效磨粒数;xavg,a是接触区有效磨粒的平均粒径;F是单颗有效磨粒的受力;Hw是元件的硬度;v是元件相对于抛光垫的相对速度;n是抛光垫峰点捕获的磨粒数;Φ(z)是正态分布函数。
基于磨粒磨损机制的材料去除模型不足之处在于:1)忽略了填充在抛光垫中的磨粒数与抛光垫材质的软硬条件有关,在其他加工条件不变的情况下,填充在软质抛光垫的磨粒数明显要高于填充在硬质抛光垫的磨粒数[13];2)忽略了接触区抛光垫峰点捕获的磨粒数与外界下压压力有关,当压力较大时,抛光垫峰点接触面积增大,捕获的磨粒数也相应增加。这两点不足导致了材料去除模型在建立过程中,一些假设条件的考虑出现了不完整性,从而导致了单颗有效磨粒的受力、参与磨削的有效磨粒数等因素计算出现了偏差。
针对以上的不足,从两个方面对材料去除模型进行改进:单颗有效磨粒的受力、接触区抛光垫峰点捕获的磨粒数。从磨粒填充角度出发,引入磨粒的抛光垫表面填充因子kc,则单颗有效磨粒的受力F[14-15]可表示为
(2)
式中:p是接触区的压力。
根据弹性力学接触模型[5,16]可得
(3)
(4)
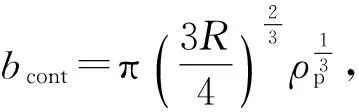
根据元件在加工中处于动态的平衡可得接触区压力为
(5)
图2是抛光颗粒嵌入抛光垫和划擦元件的放大示意图,hw为抛光颗粒嵌入元件的深度,hp为抛光颗粒嵌入抛光垫的深度,2xw为抛光颗粒同元件接触区域的直径,2xp为抛光颗粒同抛光垫接触区域的直径。根据维氏硬度计算公式,
(6)
式中:Hp是抛光垫的硬度。
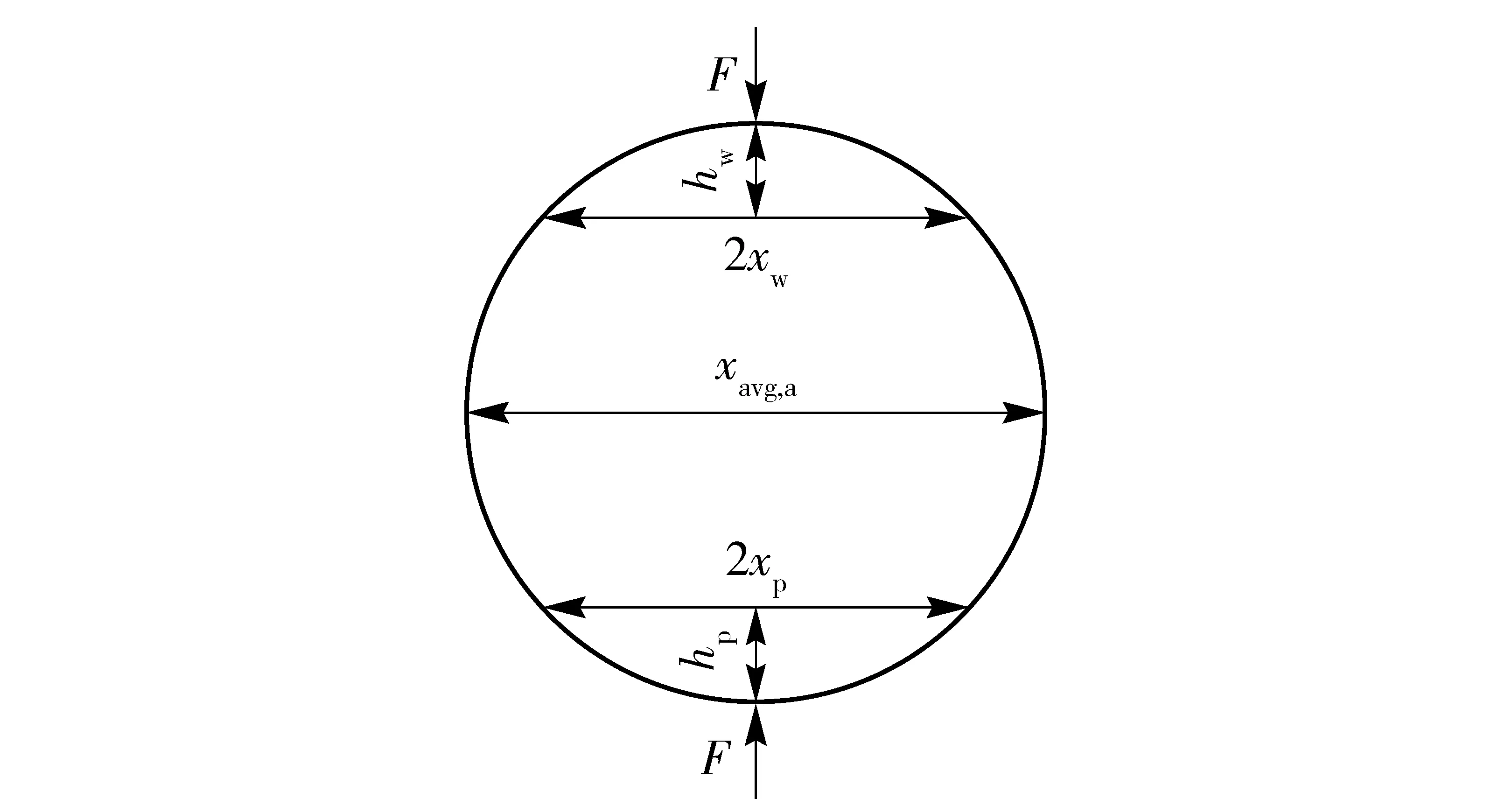
图2 单颗有效抛光颗粒嵌入抛光垫和划擦元件示意图Fig.2 Model of single effective polishing particles embedded in polishing pad and element

(7)
根据(6)式和(7)式,可以计算出单颗有效磨粒对元件表面的瞬时切除体积,如图3所示。
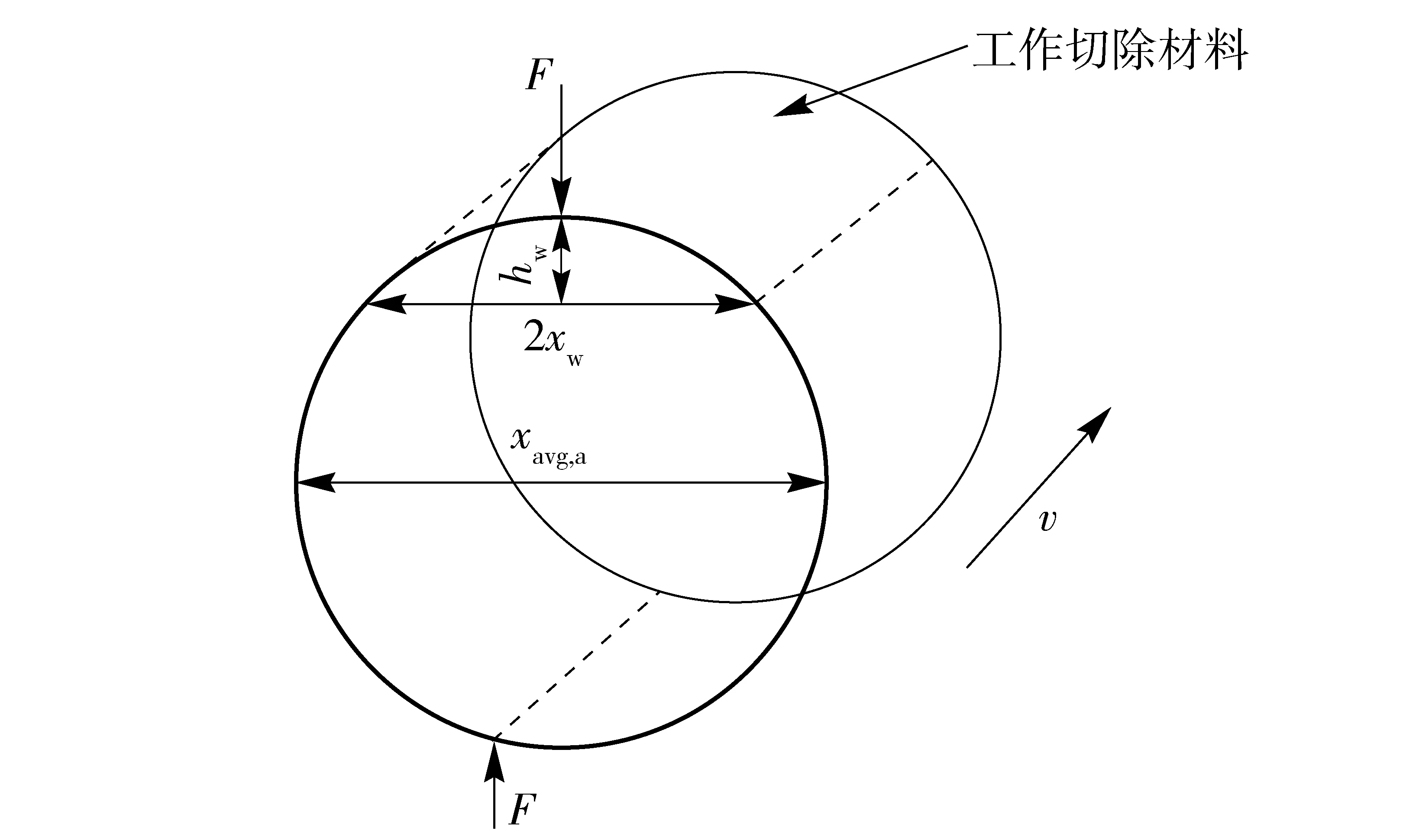
图3 单颗有效抛光颗粒瞬时切除元件材料示意图Fig.3 Model of material removed by single effective polishing particles
因此,单颗有效磨粒瞬时切除体积ΔV,
(8)
可以看出:单颗磨粒瞬时切除体积随着抛光磨粒的粒径,抛光垫弹性模量,外界所施加的压力,以及相对速度的变大而变大;单颗磨粒瞬时切除体积随着元件硬度的变小而变大。
在3个假设条件下:磨粒均匀分布在抛光液中;所有的抛光颗粒在外形上是球形的,且直径为xavg,a;镶嵌在抛光垫上的磨粒密度和在抛光液中的密度一致,计算出抛光垫峰点捕获的磨粒数n为
(9)
式中:q是面密度;χ是体积密度;Ca是抛光液中磨粒的质量分数;ρf是抛光液的密度;ρs是磨粒的密度。
当元件受到外界压力后,首先和抛光垫接触,抛光垫峰点产生弹性形变,最先嵌入抛光垫峰点的是粒径最大的磨粒(粒径为xmax),hmax是最大磨粒嵌入元件深度和嵌入抛光垫深度之和,在元件和抛光垫之间存在一个由最大粒径磨粒产生的间隔g=xmax-hmax. 随着接触状态向稳态接触过度,粒径大于g的抛光颗粒开始逐渐嵌入到抛光垫中,由于元件和抛光垫有强烈的直接接触趋势,而且抛光颗粒倾向于紧密排列,最终达到稳态接触状态。在这个过程中,间隔g始终保持不变,元件和抛光垫接触区去除元件材料的有效磨粒就是粒径大于间隔g的磨粒。
抛光颗粒粒径分布符合正态分布,概率密度函数为
(10)
式中:xavg为抛光颗粒的平均粒径;σ是粒径的标准偏差。
由此可得粒径正态分布函数Q(x)为
(11)
由正态分布的性质和快速抛光中有效磨粒的定义可得,接触区内有效磨粒数N为
(12)
(13)
有效磨粒的平均尺寸随着正向压力的变化而变化。但是,当标准偏差σ很小时,有效磨粒平均尺寸随着正向压力的改变很小。因此,有效磨粒的平均尺寸xavg,a可以认为是恒量kxavg.
将(9)式代入(12)式,并结合(8)式得到材料去除模型:
(14)
(14)式可以简化为
(15)
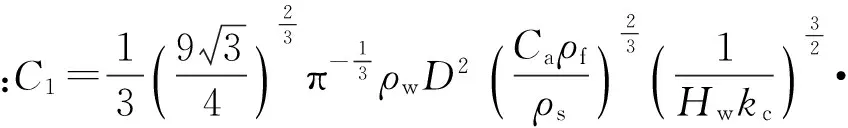
2 快速抛光材料去除模型验证
2.1 验证流程
图4所示为材料去除模型验证流程,首先将压力p1与p2下通过实验获得的材料去除量MRR1与MRR2分别代入模型,两者相除并利用数学运算软件MathCAD,结合标准正态分布的性质,计算可得C2值。将其他实验压力值及计算得到的C2值代入模型得到理论材料去除量,将实际测到的材料去除量与理论计算的材料去除量作对比,求得误差,同理求出不同实验压力下的材料去除量及误差,继而验证模型的正确性。
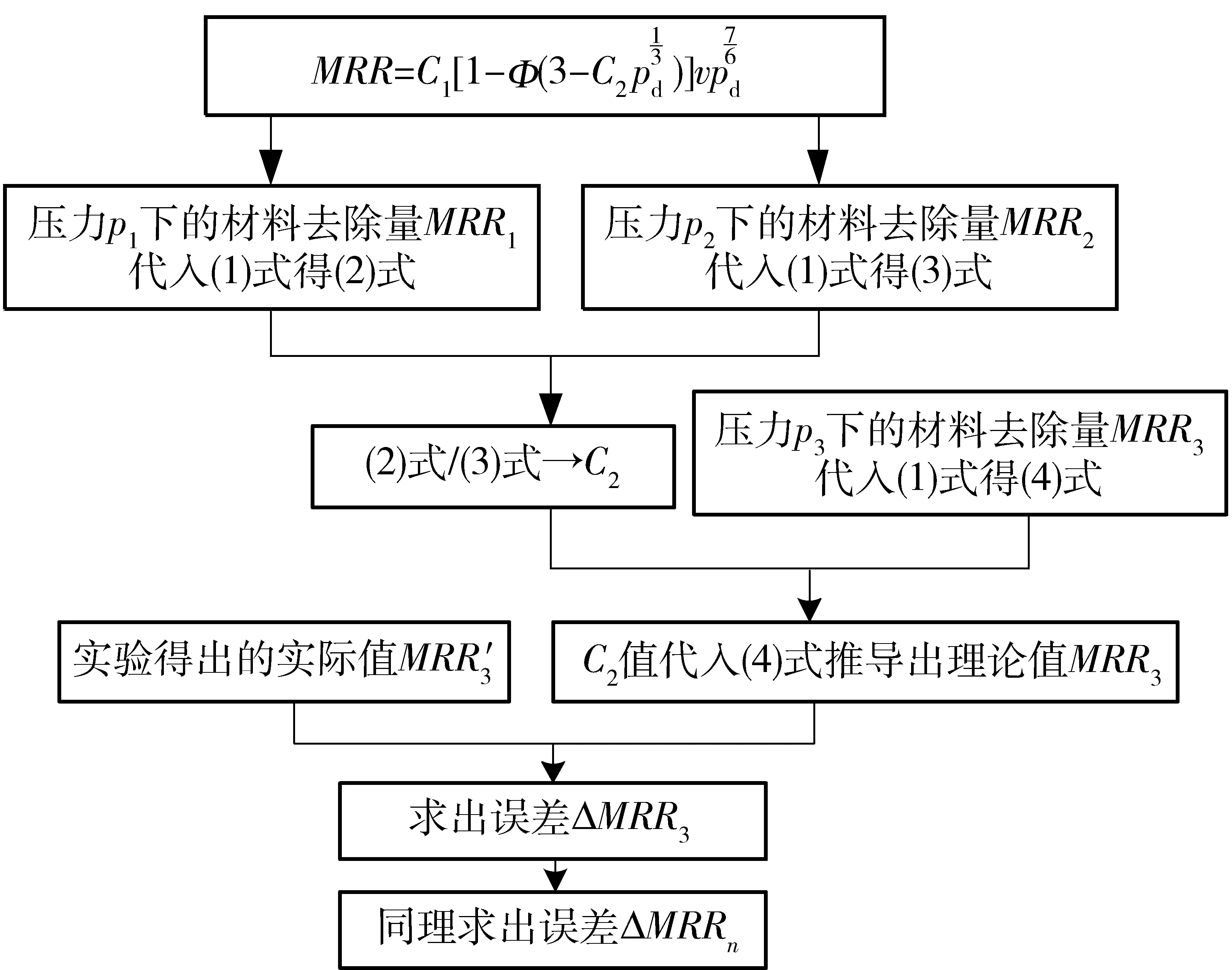
图4 MRR模型验证流程Fig.4 Verification process of MRR formula
2.2 实验样品制备
实验使用福建省三明机床有限公司产PKD330快速抛光机,采用正交实验进行材料去除模型的验证。从推导出的模型可以看出,影响材料去除的因素主要有抛光垫、抛光液、元件、相对速度和施加压力。由于在模型的验证计算过程中相对速度被约掉,而施加压力作为实验条件,所以影响因素只剩3个,即抛光垫、抛光液和元件。3个因素各选择3个水平,各因素的水平选择见表1. 对于抛光垫,考虑到抛光垫对于捕获磨粒数的影响,因此抛光垫性能特别是密度和肖氏硬度有一定差别;对于光学元件,选择了神光Ⅲ装置中最常用的熔石英和K9玻璃,与微晶陶瓷玻璃一起作为实验元件;对于抛光液,考虑到初抛和精抛等不同阶段使用的粒径不一样,因此也根据实际的工程应用加以选择。
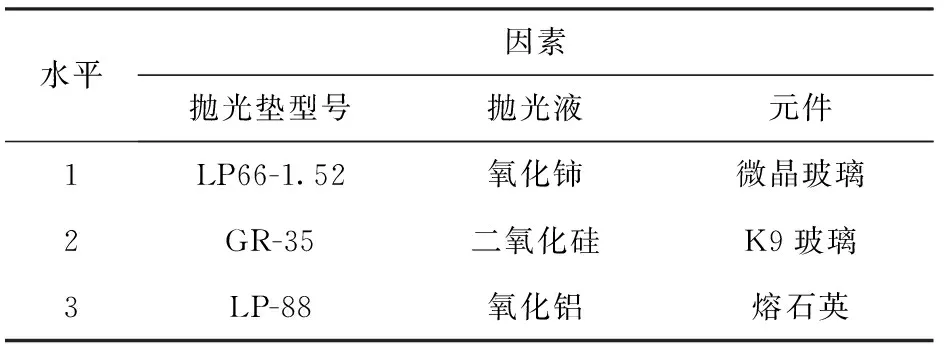
表1 水平因素编码Tab.1 Level factor coding
实验所用抛光垫的参数如表2所示。由表2可知,LP66-1.52、LP-88 和GR-35抛光垫在填充物、密度、肖氏硬度和开槽条件方面都有区别,3种抛光垫的表面微观形貌扫描电子显微镜(SEM)图如图5所示,由日本日立公司产SU70场发射SEM测得。从SEM图上可以看到,抛光垫表面上分布着气孔,气孔与气孔之间的峰点在表面呈现规律性分布。实验所用抛光颗粒粒径均由珠海欧美克仪器有限公司产LS603激光粒度分析仪测得。Al2O3抛光颗粒平均粒径为20 μm,如图6所示,CeO2抛光颗粒平均粒径为1 μm,SiO2抛光颗粒平均粒径为40 μm,3种抛光液浓度均为20%. 实验所用的微晶玻璃、熔石英玻璃和K9玻璃尺寸均为30 mm×30 mm×5 mm.
选用L9(34)作为实验的正交表,具体正交实验方案如表3所示。

表2 抛光垫参数Tab.2 Polishing pad parameters
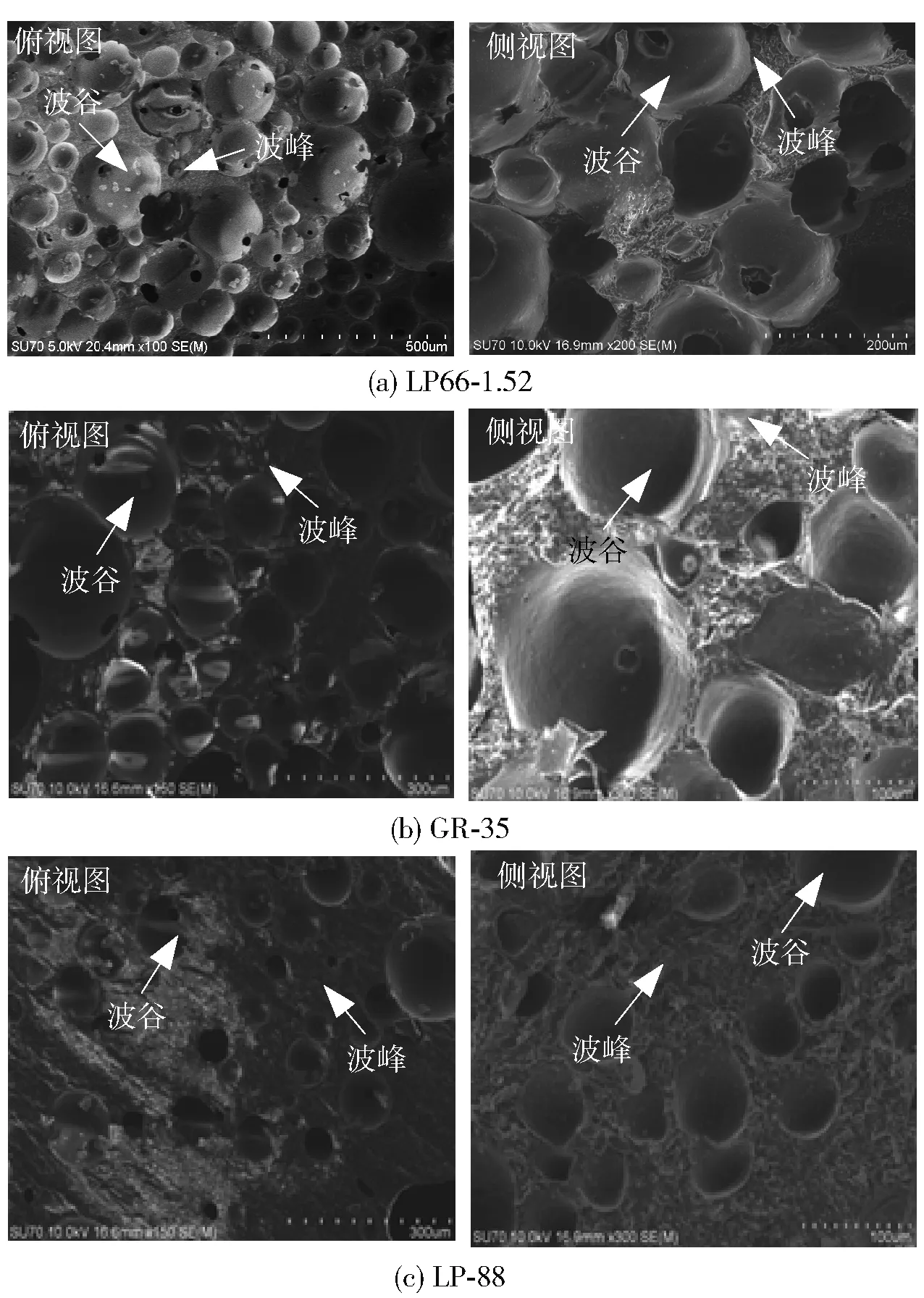
图5 抛光垫的表面微观形貌Fig.5 Surface microstructure of polishing pad
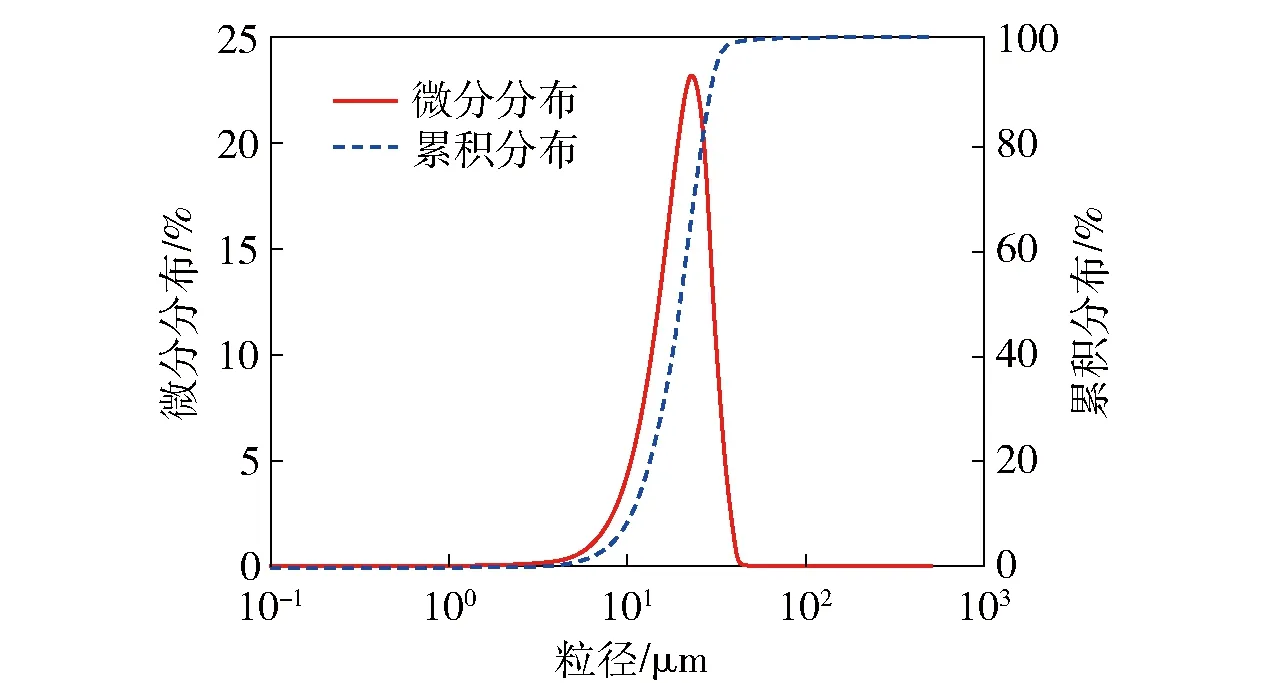
图6 粒度分布图Fig.6 Particle size distribution
每组实验在9 N、12 N、15 N和18 N不同压力条件下进行,加工时间均为1 h,元件和抛光盘转速均为100 r/min. 抛光前后使用精密天平测量每块光学元件的质量,用于计算材料去除。

表3 实验方案Tab.3 Experimental schemes
2.3 实验数据分析
经过36组实验,使用精密天平测得每块光学元件抛光前后的质量,得到每块光学元件的材料去除量,获得实验数据如表4所示。

表4 MRR 实验数据Tab.4 Experimental data of MRR mg
从表4中可以看到,抛光垫的材料性能(包括密度、肖氏硬度和开槽条件等)、元件的种类和抛光颗粒的粒径都对材料去除量有影响。例如K9玻璃的3组实验,实验7所使用的LP-88抛光垫相比较实验6所使用的GR-35抛光垫肖氏硬度要大,填充在抛光垫上的抛光颗粒较少,获得的材料去除量理论上应该较低,但是前者抛光垫密度较大,抛光垫峰点数较多,且使用的Al2O3抛光颗粒粒径也大于后者所使用的CeO2抛光颗粒,从表4中可以看出,实际的前者材料去除量较大。因此,材料去除量是几种因素共同作用的结果。
为了不失一般性,在表中的每组实验中任选两个材料去除量作为原始数据代入到模型中计算理论材料去除量,计算后得到的理论数据以及相对误差如表5所示。

表5 理论数据及相对误差Tab.5 Theoretical data and relative errors
注:表中数据为MRR(mg)/ΔMRR(%);每组实验中两处N/A代表该组实验中用于计算理论MRR的两个原始数据。
从表5中可以看到,18组材料去除量误差都在9%以内,最大的达到8.88%,最小的达到1.12%. 考虑到实验中机床的运动误差、对刀误差以及天平测量误差等误差因素,通过材料去除模型计算出来的材料去除量同实际实验得到材料去除量较为吻合,从而验证建立的光学元件快速抛光材料去除模型的正确性。需要指出的是,实验中所使用3种玻璃元件尺寸较小,质量比较轻,因此材料去除量误差的敏感度也比较大。在相同元件和其他加工条件相同的实验条件下,快速抛光依靠其自主运动性和外界施加压力,抛光效率大约是传统环形抛光的5~10倍左右。控制元件的运动路径、施加压力以及其他加工条件,400 mm直径的圆形光学元件面型精度可以达到0.5个波长,表面粗糙度可以达到1 nm以内,这些内容将在以后的论文中专门发表。
3 结论
1)针对Luo等基于磨粒磨损机制所建立的材料去除模型的不足,从单颗磨粒受力和抛光垫峰点捕获的磨粒数出发,获得量化的单颗磨粒瞬时切除体积和抛光接触区参与有效磨粒数,从而建立一种光学元件快速抛光材料去除模型。
2)通过正交实验,验证了在不同类型光学元件、抛光垫和抛光液条件下,理论预测值与实验值相比误差控制在9%以内,抛光实验的结果与理论预测的结果比较吻合,从而验证了本文所建立的光学元件快速抛光材料去除模型的正确性。
3)以本文建立的去除模型为基础,可以根据预测的研磨阶段亚表面缺陷深度,在抛光阶段严格控制加工参数,避免盲目加工,极大缩短加工时间,从而提高加工效率,满足光学元件批量生产的目标。
References)
[1] 赵东峰, 邬融, 林尊琪, 等. 超声波辅助酸蚀提高熔石英损伤阈值[J]. 强激光与粒子束, 2015, 27(1):105-110. ZHAO Dong-feng, WU Rong, LIN Zun-qi,et al.Acid etching combined with ultrasonic for improving laser damage threshold of fused silica[J]. High Power Laser and Particle Beams, 2015, 27(1):105-110.(in Chinese)
[2] 王洪祥, 朱本温, 陈贤华, 等. 抛光工艺参数对熔石英元件低频面形精度的影响[J]. 强激光与粒子束, 2015, 27(4):042001-1-042001-5. WANG Hong-xiang, ZHU Ben-wen, CHEN Xian-hua, et al. Impact of polishing process parameters on the low frequency surface accuracy of fused silica optics[J]. High Power Laser and Particle Beams, 2015, 27(4):042001-1-042001-5.(in Chinese)
[3] Mu Y, Zhuang Y, Sampurno Y,et al. Effect of pad groove width on slurry mean residence time and slurry utilization efficiency in CMP[J]. Microelectronic Engineering, 2016, 157:60-63.
[4] Suratwala T I, Wong L L, Miller P E, et al. Sub-surface mechanical damage distribution during grinding of fused silica[J]. Journal of Non-Crystalline Solids, 2006, 352: 5601-5617.
[5] Luo J F, Dornfeld D A. Material removal mechanism in chemical mechanical polishing: theory and modeling[J]. IEEE Transactions on Semiconductor Manufacturing, 2001, 14(2):112-133.
[6] Runnels S R, Eyman L M. Tribology analysis of chemical mechanical polishing[J].Journal of Electrochemical Society, 1994, 141(6):1698-1701.
[7] Borst C L, Thakurta D G, Gill W N, et al. Surface kinetics model for SiLK chemical mechanical polishing[J]. Journal of Electrochemical Society, 2002, 149(2):118-127.
[8] Zhao Y W,Chang L, Kim S H. A mathematical model for chemical mechanical polishing based on formation and removal of weakly bonded molecular species[J]. Wear, 2003, 254(3/4):332-339.
[9] Zhao Y W,Chang L. A micro-contact and wear model for chemical-mechanical polishing of silicon wafers[J]. Wear, 2002, 252(3/4):220-226.
[10] Moon Y. Mechanical aspects of the material removal mechanism in chemical mechanism polishing (CMP)[D]. Berkeley: University of California at Berkeley, 1999.
[11] Jiun Y L. Mechanics, mechanisms, and modeling of the chemical mechanical polishing process[D]. Massachusetts: Massachusetts Institute of Technology, 2001.
[12] Yang W, Guo Y B, Li Y G, et al. Pressure and velocity dependence of the material removal rate in the fast polishing process[J]. Applied Optics, 2007, 47(33):6236-6242.
[13] Marquez J J, Perez J M, Rios J, et al. Process modeling for robotic polishing[J]. Journal of Materials Processing Technology, 2005, 159(1):69-82.
[14] Cook L M. Chemical processes in glass polishing[J]. Journal of Non-Crystalline Solids, 1990, 120(1/2/3):152-171.
[15] Zhang F. Submicron particle adhension and removal in chemical-mechanical polishing and wafer cleaning process[D]. Potsdam: Clarksom University, 2002.
[16] Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1966, 295(1442): 300-319, 1996.
Research on Material Removal Model of Optical Elements Based on Fast Polishing Technology
LIN Tao1, YANG Wei1, WANG Jian2
(1.School of Aerospace Engineering, Xiamen University, Xiamen 361005, Fujian, China; 2.Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, Sichuan, China)
In order to accurately control the material removal in polishing stage, and achieve the deterministic polishing processing of toptical element, the quantitative mean volume removed by a single particles per unit time and the number of the active particles on the wafer-pad interface are obtained from the force applied on an abrasive particle and the number of all particles on the wafer-pad contact area. An optical element fast polishing material removal model is established based on the analysis of fast polishing principle and fast polishing material removal mechanism. Research shows that, under the experimental conditions of different polishing liquids, polishing pads and optical elements, the theoretically predicted results of the material removal model are well coincident with the experimental results, and the error of material removal can be controlled within 9%. The proposed model is verified to be suitable for the optical element fast polishing technology, thus deterministically controling the fast polishing time and efficiency.
manufacturing technology and equipment; optical element; fast polishing; material removal model
2016-04-22
国家自然科学基金项目(51675453);福建省高等学校创新能力提升计划项目(2013年)
林涛(1989—),男,硕士研究生。E-mail: 519023733@qq.com
杨炜(1981—),男,助理教授,硕士生导师。E-mail:oncefly@126.com
TN205
A
1000-1093(2017)03-0527-07
10.3969/j.issn.1000-1093.2017.03.015
