基于凸优化的水下载体定位研究

曹俊， 郑翠娥， 孙大军， 张殿伦

(1.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001; 2.哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001)

基于凸优化的水下载体定位研究

曹俊1,2， 郑翠娥1,2， 孙大军1,2， 张殿伦1,2

(1.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001; 2.哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001)

基于单信标测距的定位方法，是水声定位技术一个新的研究方向，具有重要应用价值。针对单信标测距定位问题最小二乘结构，对高度非凸的测距定位方程首次提出了基于凸优化的解算方法。对带有误差的测距量测方程添加不等式约束条件，将其改写为有约束的解算方程；对目标函数和约束条件进行放射近似，将其进行凸化处理；引入松弛变量和罚函数，降低对迭代初值的敏感度。仿真结果表明：对于不同量级的初值误差，定位结果的差别在厘米量级，所提算法不需要可靠的初值即能迭代收敛得到高精度的定位结果；信标与圆形航迹的圆心距离越近，定位精度越高。通过湖上试验，进一步验证了所提算法的有效性。

信息处理技术； 单信标测距； 虚拟信标； 凸优化； 约束条件； 罚函数

0 引言

随着海洋开发活动进程的加快，水下载体定位的重要性越来越强。基于单信标距离测量的定位方式只需要一个海底声信标，占用资源少，具有重要的应用价值[1-4]，最近吸引了越来越多专家学者的研究兴趣。基于单信标距离测量的定位解算方法中，文献[5]最早提出使用最小二乘法解算出无人水下潜航器(UUV)的水平初始位置，通过直接降阶的方式将定位方程两两相减消除二次项，构成线性方程组，从而实现对UUV位置的求解。文献[6]通过松弛最小二乘模型为半定规划问题，但是经过这样处理的定位方案在最小二乘意义上不再是最优估计。文献[7]提出了基于距离平方的最小二乘定位方案，但这个方法只是近似最大似然估计，所以得到的定位结果仍然是次优的。基于最小二乘法的定位方法是一种重要的解决方案，它不仅能够提供低复杂度的解决过程，还能够得到可靠的定位估计精度。众所周知，最小二乘法是凸优化问题的一种特殊形式，尽管关于最小二乘问题的求解技术已经有比较成熟的技术，但是带有测量误差的最小二乘测距定位方程是高度非凸的。如果能将非凸定位方程函数凸化，转化成凸优化的问题，就能有效地进行求解[8]。

本文针对单信标测距定位问题，首次针对定位问题中的最小二乘结构提出了基于凸优化的解算方法。首先，根据最小二乘理论推导出定位解算的目标函数，将目标函数经过公式推导和形式转换，使之与凸优化理论中的凸差(DC)结构形式相符合，并根据测距误差情况添加约束条件。DC结构问题可以利用凹凸处理(CCP)算法，通过目标函数凸化将DC问题转化成凸优化问题求解，进而达到利用凸优化的方法解决定位方程的目的。其次，针对CCP算法对初值要求比较高(初值必须在可行域内)的缺点，引入序列无约束极小化的罚函数，放宽对初始点要求的优点，引入罚函数，放宽CCP算法对初值的要求，增强算法的适应性。最后，对提出的基于凸优化理论的定位解算方法进行了仿真分析和湖试数据分析，进一步验证了所提算法的有效性。

1 基于凸优化的单信标测距定位原理

单信标测距定位系统主要由海底声信标和安装在水下载体上的测距仪组成。海底声信标的位置事先标定得到，利用声信号传播的往返时间可以确定被定位载体与海底声信标之间的距离[9-10]。原理上，单次距离测量不能确定水下载体的具体位置，所以需要结合水下载体工作时的运动参数如速度和姿态来实时解算出水下载体的位置，如图1所示。其中VT1、VT2直到VTn-1不是真实存在的，它们是根据水下载体两个测距周期之间的载体位移虚拟出来的，故也可称之为虚拟信标。例如Xb(n-1)至Xbn的位移为ΔXb(n-1),bn=vb(n-1),bnT，则虚拟信标VTn-1的位置为VTn+ΔXb(n-1),bn，v为大地坐标系下的水下载体运动速度，T为测距周期。解算第n个测量点需要利用测量点1～n的测距信息和载体运动参数，解算第n+1个测量点需要利用测量点2～n+1的测距信息和载体运动参数，依此类推基于单信标测距完成对水下载体的跟踪定位[11]。

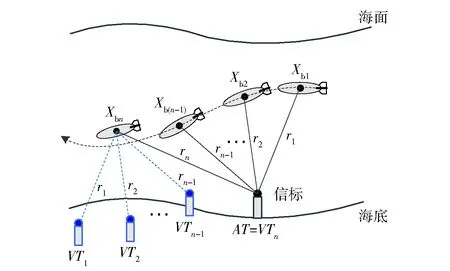
图1 单信标测距定位原理Fig.1 Single beacon ranging and positioning principle

定位方程中，水下载体与信标之间存在噪声干扰，则第i个测量点对应的距离测量方程满足

ri=‖x-xti‖+εi,i=1,2,…,n，

(1)

式中：虚拟信标VTi的坐标为xti；水下载体要定位的位置Xbn的坐标为x；ri为水下载体与第i个虚拟信标之间的距离；εi表示水下载体与第i个虚拟信标进行距离测量时存在的未知噪声干扰，该未知噪声干扰由测时误差和声速误差共同决定。

单信标测距定位问题最初的形式是一个非凸的优化问题，可以描述为根据有噪声干扰的测距信息估计水下载体位置的问题，定位问题就是基于距离的最小二乘估计问题：

(2)

为了对定位问题进行分析，本文首先介绍DC问题的标准形式：

(3)

式中：x∈Rn，并且fi和gi都是凸函数。

在CCP优化过程中，通过将DC问题中的gi(i=0,…,n)仿射近似，可以利用迭代方法进行最优值求解。转化后的形式为

(4)

式中：xk为第k次迭代时的水下载体位置迭代量。

首先找到一个可行域内的初值x0，通过迭代过程，求解CCP结构方程，从而得到DC问题的最优解。

根据DC问题和CCP优化的定义，本文对单标定位最小二乘估计的目标函数展开去除常数项后得到

(5)

对展开后的目标函数，对照DC结构的标准形式有如下定义：

(6)

则目标函数可以表示为F(x)=f(x)-g(x)的形式，因为其中的f(x)和g(x)都是凸函数，所以目标函数满足DC结构的形式。

g(x)在xk处的估计值可以表示为

(7)

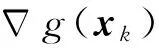
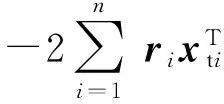
得到目标函数的凸化之后的形式为

(8)

(9)

不等式展开后形成两个新的不等式，‖xk-xti‖-ri-δi≤0和ri-δi≤‖xk-xti‖.

第1个不等式的fi(x)=‖xk-xti‖-ri-δi，gi(x)=0，满足凸优化的约束条件fi(x)-gi(x)≤0；第2个不等式的fi(x)=ri-δi，gi(x)=‖xk-xti‖. 对gi(x)=‖xk-xti‖在xk处进行线性化处理得到i(x,xk)=‖xk-xti‖+∂‖xk-xti‖T(x-xk)，则第2个不等式可以写为-‖xk-xti‖-∂‖xk-xti‖T(x-xk)+ri-δi≤0，满足于凸优化的约束条件fi(x)-i(x,xk)≤0. 所以，第k次迭代的时候，凸优化问题可以描述为

(10)

CCP算法中要求初值必须是可行域内的值，为了降低初值的限制，引入非负的松弛变量si≥0和i≥0，用它们来代替约束条件右侧的0来提升上界，这就形成了新的有约束条件的凸优化问题：

(11)

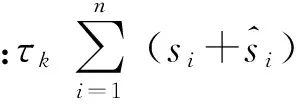
若xk是可行域内的值，则松弛变量满足si=0和i=0，且新的凸优化问题与原来的凸优化问题是一样的。若xk不是可行域内的值，则松弛变量满足si>0和i>0，且0，新的凸优化问题与原来的凸优化问题相比多了).之所以被称为惩罚项，是因为随着迭代次数的增加，τk不是一个确定的参数，而是递增的，这便具有了惩罚的含意。当xk不是可行域内值的时候，目标函数被逐渐增大，求极小值又期望将xk拉回到可行域内，最终xk会被拉到不可行域和可行域的边界处，松弛变量si和i也会相应地减小直至为0，进而在可行域内求得xk的最优解。所以，松弛变量si和i的引入会放宽初值限制，在约束条件中引入单调递增的惩罚因子τk，算法的松弛变量能够减小得更快，当松弛变量减小到特别小的时候，迭代过程能很快变得可行。

综上分析，本文提出的基于凸优化单信标测距定位算法详细流程如表1所示。

表1 基于凸优化的定位算法流程Tab.1 Positioning algorithm based on convex optimization

表1中，测距误差边界δ的值选择为信标测距精度的3倍；初始罚因子τ0=1；惩罚因子增长因子μ在5～10之间选择；迭代次数最大值选择为50次。

综上分析，只要是基于信标测距的定位导航系统，都能够使用本文提出的基于凸优化的解算方法。并且本文算法具有两方面优点：一方面，对于存在噪声干扰的测距量测量，根据统计得到的测距精度对测距方程添加测距误差边界条件；另一方面，当不知道载体比较准确的初始位置时，也能够迭代解算得到载体位置，放宽了对初始位置的要求。

2 计算机仿真分析

本节中，在Matlab环境中对基于凸优化的单信标测距定位算法进行仿真分析，验证所提出的算法的有效性，并对相关仿真结果进行分析。仿真参数为：海底布放的单只声信标的坐标为AT=(0 m,0 m,100 m)。水下载体在恒定深度为100 m的深度作环形机动，前向运动速度恒定为1 m/s. 对布放的单只信标的测距周期为10 s. 添加呈高斯分布的随机测距误差N=(0 m,1.52m)。水下载体按圆形航迹机动完成后，根据测距信息和虚拟信标的位置实现对水下载体终点位置的定位。

为了分析本文算法对定位精度的提高，将本文算法与最小二乘法进行比对。接收信标信号的信噪比高的时候，相应的测距误差小；接收信标信号的信噪比低的时候，相应的测距误差大。本文算法与最小二乘法的对比见表2，采用蒙特卡洛法进行1 000次实验。从表2中可知，对于不同量级的测距误差，本文算法的定位精度都高于最小二乘法的定位精度；测距误差越大，本文算法对定位精度的提高与最小二乘法定位精度的比值越高。

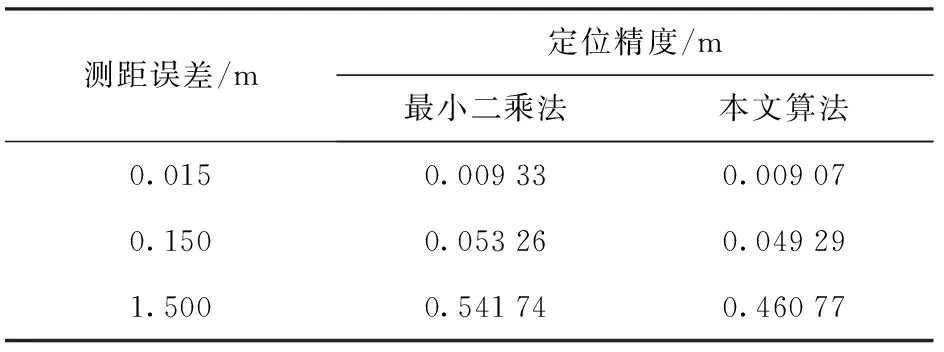
表2 本文算法与最小二乘法对比Tab.2 Comparison between the algorithm proposed in this paper and the least square method

为了验证迭代初值对定位结果的影响，对水下载体的迭代初值添加几十米量级和几百米量级的初值误差。图2为使用本文提出的算法得到的圆形航迹终点的定位结果。图2(a)对水下载体的迭代初值添加东向20 m和北向30 m的初值误差，本文算法对圆形航迹终点定位结果的根均方误差为0.684 55 m. 图2(b)对水下载体的迭代初值添加东向200 m和北向300 m的初值误差，本文算法对圆形航迹终点定位结果的根均方误差为0.664 52 m. 对于航位推算的定位结果，在不存在其他误差的情况下，定位误差的大小与初始位置误差大小相同。比对两幅图可以看出，对于不同量级的初值误差，定位结果的根均方误差的差别在厘米量级，本文算法不需要可靠的初值即能迭代收敛得到高精度的定位结果。

图2 迭代初值误差对定位结果影响Fig.2 Influence of iterative initial value error on positioning results

为了验证信标位置与圆形航迹圆心距离对定位结果的影响，信标与圆形航迹圆心分别相距0 m和35 m. 图3为使用本文提出的算法得到的圆形航迹终点的定位结果。图3(a)信标与圆形航迹圆心相距0 m，本文算法对圆形航迹终点定位结果的根均方误差为0.383 21 m. 图3(b)信标与圆形航迹圆心相距35 m，本文算法对圆形航迹终点定位结果的根均方误差为0.421 86 m. 图2(a)信标与圆形航迹圆心相距70 m. 比对图3(a)、图3(b)和图2(a)可以看出，信标与圆形航迹的圆心距离越近，定位精度越高。

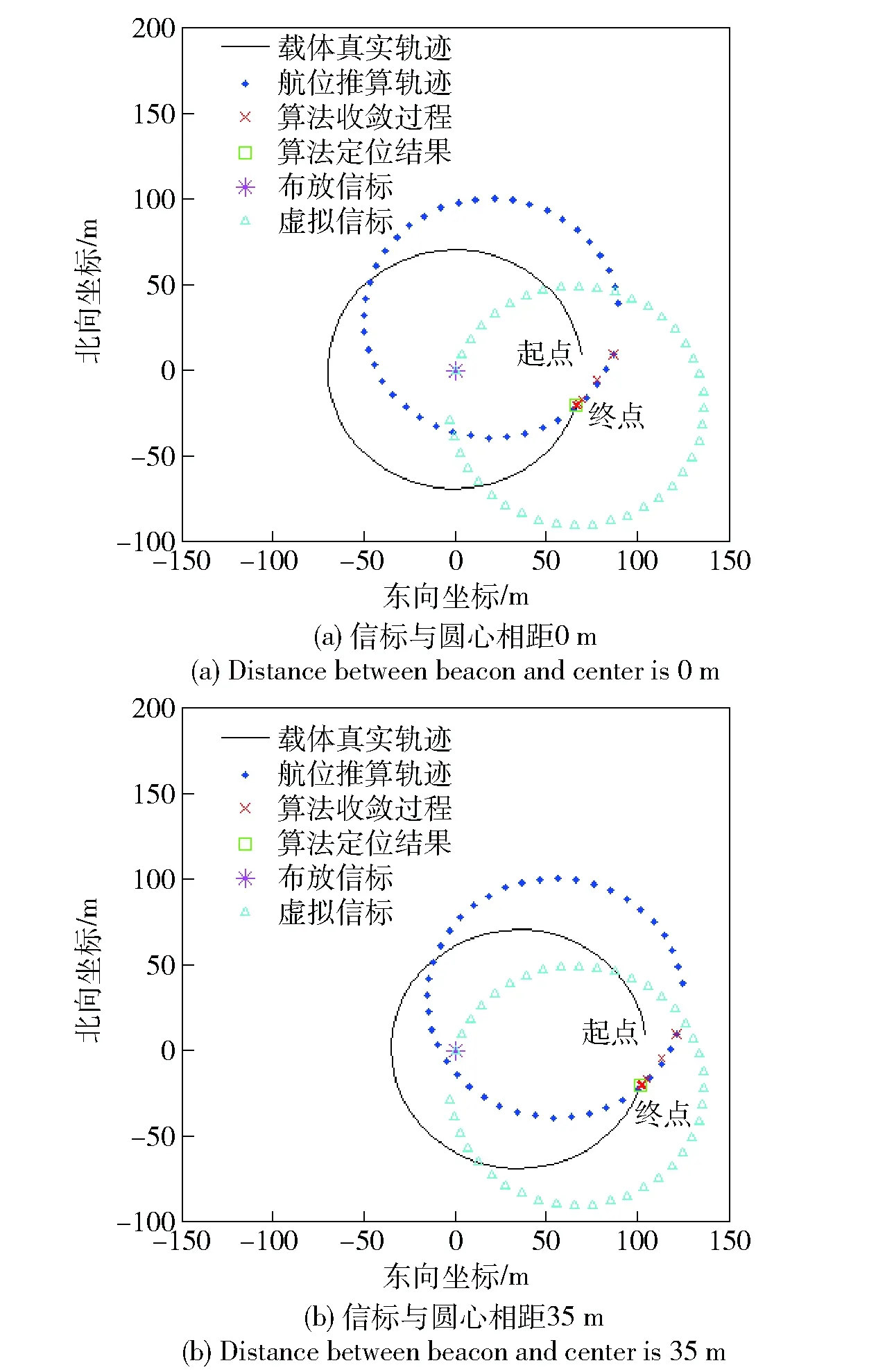
图3 信标位置与圆心距离对定位结果影响Fig.3 Influence of distance between beacon and center on the positioning results

3 湖试数据分析

2015年9月在某湖面进行了单信标测距定位的外场湖试试验。试验地点的水深约为43 m. 试验平台为小型旅游船。水面试验设备包括：法国IXBLUE公司的RAMSES6000声学测距系统，测距系统的时延测量精度能达到100 μs的水平，测距系统为分体式结构。法国IXBLUE公司的Octans高精度罗经，航向角可以保持0.1°正切维度的动态精度，分辨率0.01°；横滚角和俯仰角可以保持0.01°的动态精度，分辨率0.001°. 美国RDI公司的声学多普勒测速仪ADCP/DVL，600 kHz工作主频的情况下作用高程为0.7～90 m，载体航行速度v的情况下，测量的对水底速度的精度大概为±3‰·v±0.002 m/s. 瑞士Leica公司的Leica 1200型差分全球定位系统(GPS) ，在RTK模式下工作时对低速运动目标的定位精度能够达到2～3 cm.

水面试验设备安装示意图如图4所示。罗经固定于试验船船舱内，偏航方向正对试验船船艏。多普勒测速仪通过三脚架固定安装在试验船右舷后侧，相对于罗经向下0.47 m. GPS天线安装在三脚架顶端，相对于罗经向上2.87 m. 声学测距系统的分体式换能器头通过钢管固定安装在试验船左舷后侧，相对于罗经向下2.78 m.

图4 水面试验设备安装示意图Fig.4 Schematic diagram of surface test equipment installation

水下试验设备为法国IXBLUE公司的RTA系列声信标，声信标的时延测量精度能达到100 μs的水平，声信标为一体式结构，如图5(a)所示。声信标通过锚系结构布放于湖底，锚系结构如图5(b)所示。声信标的释放机构朝下，释放机构卡住O型释放环，释放环通过软绳与沉块相连，绳长5 m；声信标的换能器头朝上，通过软绳与浮球相连，绳长5 m，浮球提供的浮力使声信标能够尽量保持垂直状态。水面接一浮球，用于标识声信标的大概位置，便于水面试验船围绕声信标走航迹。

图5 声信标及锚系结构Fig.5 Acoustic beacon and anchor system structure

试验中，水面试验船在水面浮球外侧作环形机动，半径大概为35 m. 声学测距系统对声信标的测距周期为5 s. 迭代初值添加东向20 m和北向30 m的初值误差。将终点处的定位结果与GPS真值进行比较来评价定位精度。图6为使用本文提出的算法得到的圆形航迹终点的定位结果。图6(a)信标在圆形航迹外侧，本文算法对圆形航迹终点定位结果的根均方误差为4.382 3 m. 图6(b)信标在圆形航迹内侧，本文算法对圆形航迹终点定位结果的根均方误差为2.676 5 m. 比对两幅图可以看出，信标在圆形航迹内侧的定位精度高于信标在圆形航迹外侧的定位精度，这与仿真分析的结论一致。

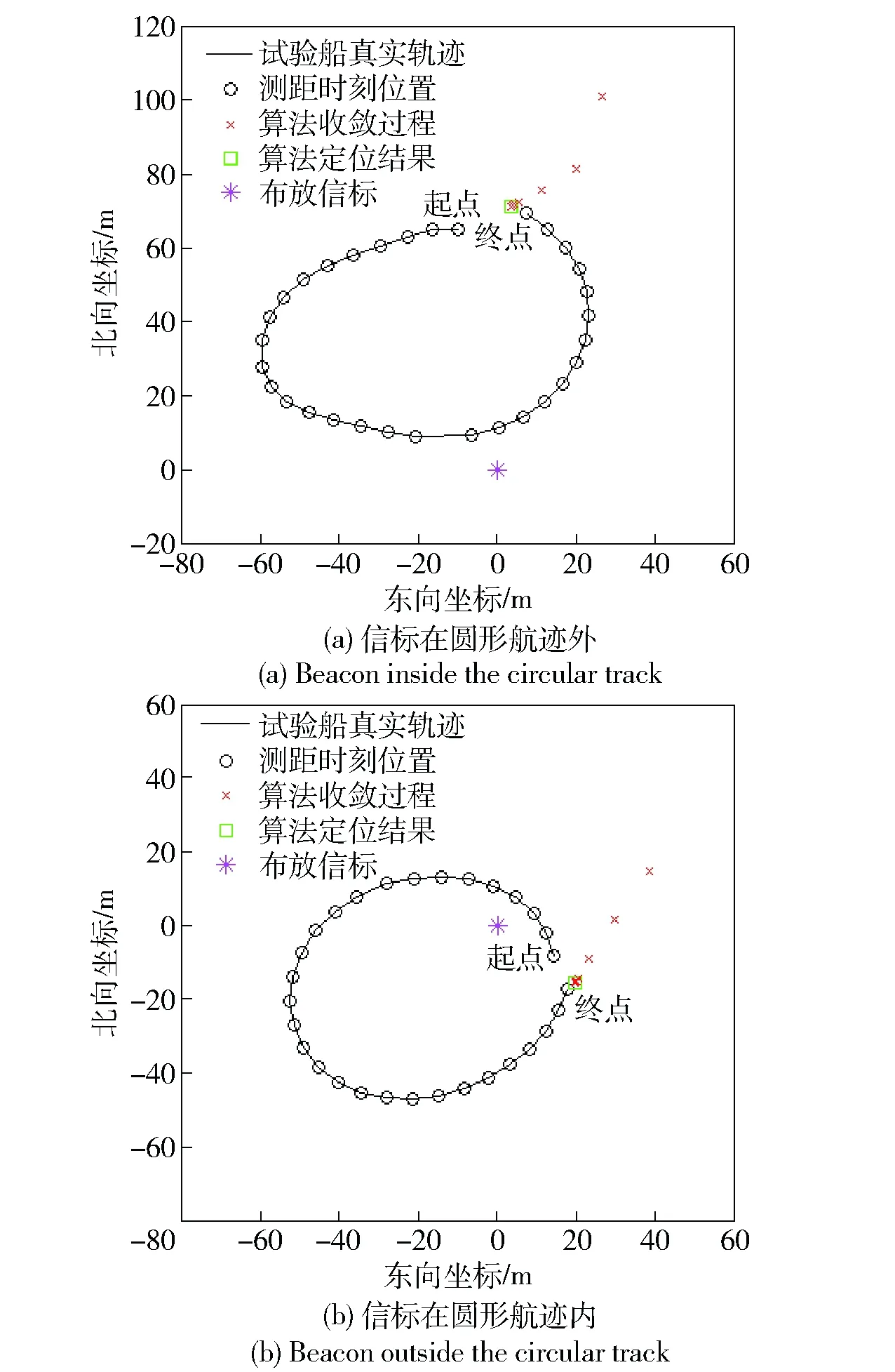
图6 湖试结果Fig.6 Lake trial results

4 结论

针对水下载体的单信标测距定位研究，本文提出了一种基于凸优化的单信标测距定位解算方法：1)对高度非凸的测距定位方程进行凸优化处理，得到凸的目标函数，得到全局最优解；2)考虑测距系统由于噪声干扰存在的测距误差，添加不等式约束条件；3)引入罚函数，降低对迭代初值的敏感度。

对提出的定位解算方法进行仿真分析，仿真结果表明：1)对于不同量级的初值误差，定位结果的根均方误差的差别在厘米量级，本文算法不需要可靠的初值即能迭代收敛得到高精度的定位结果；2)信标位置与圆形航迹圆心距离不同时，定位结果的根均方误差的差别在分米量级，信标与圆形航迹的圆心距离越近，定位精度越高。

通过湖上试验，进一步验证了本文所提算法的有效性。

References)

[1] Gaurav C, Arpita S, Twinkle T, et al. Conditions for target tracking with range-only information[J]. Robotics and Autonomous Systems, 2016, 75: 176-186.

[2] 孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨[J]. 海洋技术学报, 2015,34(3): 64-65. SUN Da-jun, ZHENG Cui-e. Discussion on development trend of underwater acoustic navigation and positioning technology[J]. Journal of Ocean Technology, 2015,34(3): 64-65. (in Chinese)

[3] 郭雅静, 李春雨, 张东升, 等. 基于航位推算/水声定位系统的水下拖体组合导航方法[J]. 海洋地质前沿, 2015, 31(6): 63-67. GUO Ya-jing, LI Chun-yu, ZHANG Dong-sheng,et al. The integrated navigation method by underwater towing body based on dead reckoning/hydroacoustic positioning system[J]. Marine Geology Frontiers, 2015, 31(6): 63-67. (in Chinese)

[4] Hegrenas O, Gade K, Hagen O K, et al. Underwater transponder positioning and navigation of autonomous underwater vehicles[C]∥MTS/IEEE Biloxi-Marine Technology for Our Future: Global and Local Challenges. Biloxi, MS, US: MTS, 2009.

[5] Alexander P S. The AUV positioning using ranges from one transponder LBL [C]∥Proceedings of the 1995 MTS/IEEE Oceans Conference. San Diego, CA, US: MTS,1995:1620-1623.

[6] Vandenberghe L, Boyd S. Semidefinite programming[J]. SIAM Review, 1996,38(1): 40-45.

[7] Beck A, Stoica P, Li J. Exact and approximate solutions of source localization problems[J]. IEEE Transactions on Signal Processing, 2008,56(5): 1770-1778.

[8] Yuille A L, Rangarajan A. The concave-convex procedure[J]. Neural Computation, 2003, 15(4): 915-936.

[9] 刘明雍, 李闻白, 刘富樯, 等. 基于单信标测距的水下导航系统可观测性分析[J]. 西北工业大学学报, 2011, 29(1): 87-92. LIU Ming-yong, LI Wen-bai, LIU Fu-qiang, et al. Observability analysis of underwater navigation system based on single beacon ranging [J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 87-92. (in Chinese)

[10] 严卫生, 房新鹏, 崔荣鑫. 单信标测距AUV水下定位系统观测性分析[J]. 中南大学学报:自然科学版, 2012, 43(8): 3085-3090. YAN Wei-sheng, FANG Xin-peng, CUI Rong-xin. Observability analysis of single-beacon underwater localization of autonomous underwater vehicle [J]. Journal of Central South University:Natural Science Edition, 2012,43(8): 3085-3090. (in Chinese)

[11] Baccou P, Jouvencel B. Homing and navigation using one transponder for AUV, post-processing comparisons results with long base-line navigation [C]∥IEEE International Conference on Robotics and Automation.Washington, DC, US: IEEE,2002.

Research on the Positioning of Underwater Vehicle Based on Convex Optimization

CAO Jun1,2， ZHENG Cui-e1,2， SUN Da-jun1,2， ZHANG Dian-lun1,2

(1.College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China;2.Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

The localization method based on single beacon ranging is a new research direction of underwater acoustic positioning technology. A method based on convex optimization is proposed for the first time to solve the least square structure for the single beacon ranging and locating. An inequality constraint condition is added to the ranging equation with errors, and the ranging equation is reformulated as a constrained solution equation. The objective function and constraint condition are approximated by radiation, and the convex processing is carried out. The slack variable and penalty function are introduced to reduce the sensitivity of iteration initial value. Simulated results show that the difference of positioning results is in centimeter order of magnitude for different magnitudes of initial errors. The proposed algorithm can be iterated convergence to get high accuracy of the positioning results without reliable initial value. When the beacon is close the center distance of circular track, the positioning accuracy is higher. The effectiveness of the proposed algorithm is verified by experiments on the lake.

information processing technology; single beacon ranging; virtual beacon; convex optimization; constraint condition; penalty function

2016-07-04

国家自然科学基金项目(61531012)；国家国防科技工业局技术基础科研项目(B2420133002)

曹俊(1987—), 男, 博士研究生。E-mail: caojun1105@sina.cn

张殿伦(1967—), 男, 教授, 博士生导师。E-mail: zhangdianlun@hrbeu.edu.cn

TB568

A

1000-1093(2017)03-0520-07

10.3969/j.issn.1000-1093.2017.03.014