基于灰色残差修正理论的目标航迹预测方法

邸忆， 顾晓辉， 龙飞

(1.南京理工大学 机械工程学院， 江苏 南京 210094； 2.贵州大学 智能信息处理研究所， 贵州 贵阳 550025)

基于灰色残差修正理论的目标航迹预测方法

邸忆1， 顾晓辉1， 龙飞2

(1.南京理工大学 机械工程学院， 江苏 南京 210094； 2.贵州大学 智能信息处理研究所， 贵州 贵阳 550025)

针对灰色理论在智能反坦克子弹药对地面目标航迹预测的精度问题，提出两种灰色残差修正的航迹预测模型：标准灰色残差修正模型(GRMM)和基于灰色Verhulst模型理论的灰色Verhulst残差修正模型(GVRMM)。建立目标航迹灰色预测模型，并分析了灰色模型的局限性；对预测值与测量值的残差序列采用GRMM和GVRMM两种模型进行了在线预估，并利用残差预测值对航迹预测值进行实时修正。通过仿真实验验证了基于在线残差修正机制的方法能够有效减少目标跟踪误差，GVRMM的误差修正效果更加明显，具有良好的实用性。

兵器科学与技术； 目标跟踪； 航迹预测； 残差修正； 灰色残差修正模型

0 引言

智能反坦克(BAT)子弹药是一种新型智能弹药系统，主要在弹体飞行过程中采用声/红外等被动式复合探测手段对地面装甲目标进行自动搜索、识别定位、航迹预测直至摧毁。BAT子弹药关键技术是目标探测识别及快速跟踪，通过弹载探测装置实时探测弹目相对距离、方位角和俯仰角，再由测量信息准确预测目标航迹。

在传统目标跟踪航迹预测中，最常用的估计方法为卡尔曼滤波、粒子滤波及其改进算法[1-2]，通常需建立目标航迹模型和测量模型，通过测量值和状态值的不断迭代进行目标航迹预测和状态预估。此类算法在现代火控系统、主动雷达跟踪系统中表现出了良好的性能，但是在BAT子弹药被动探测及弹载跟踪系统中，卡尔曼滤波、粒子滤波等算法的计算复杂度很可能超出系统承载能力，并不能实现良好的预测性能。对于运动目标跟踪而言，不同的目标运动模式需要选取相应的跟踪模型，基于多模型假设的目标跟踪方法[3-4]可以很好地解决机动目标跟踪问题，而多模型假设目标跟踪方法涉及模型集构建和模型选择，并且传统算法大多依赖充足的先验知识或测量数据，不能满足弹药对目标跟踪的灵活性要求。因此，针对BAT子弹药的目标跟踪系统迫切需要一种数据量要求较低，计算速度快，航迹预估精度良好的预测算法。

灰色理论[5]是由国内著名学者邓聚龙教授最早提出的一门涉及多学科的数学理论系统，已在民用及军事装备等领域[6-8]得到了广泛的应用。文献[7]将一种优化的灰色模型与信息融合理论相结合，并在导弹装备预测中取得较好的效果；文献[8]首次将灰色预测理论引入到反直升机智能雷探测跟踪系统，给出一种基于灰色理论的直升机航迹预估方法，实现了在少数据、贫资料状况下的直升机飞行航迹预估。然而对于在线连续时序预测问题，传统灰色系统理论本身的稳定性表现并不尽如人意，因此，出现了相关有针对性的改进方法[9-12]。本文首先对传统灰色模型GM(1,1)本身的局限性进行了分析；其次，针对传统算法的缺陷及误差问题，并未进行算法本身的改进，而是在灰色模型中引入在线残差修正策略，建立了两种残差修正预测模型：标准灰色残差修正模型(GRMM)和灰色Verhulst残差修正模型(GVRMM)，可快速更新航迹预测值，防止目标跟踪过程中的误差累积，进一步提升预测精度，对于目标航迹预测有着积极的理论参考和工程应用价值。

1 灰色航迹预估模型

设原始测量数据列[8]为

{x(0)(i)}，i=1,2,…,N，

(1)

式中：x(0)(i)可以表示为BAT弹体与目标之间的径向距离、方位角或者俯仰角测量值。

一次累加生成算子(AGO)序列

{x(1)(i)}，i=1,2,…,N，

(2)

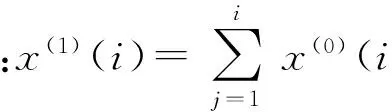
建立GM(1,1)模型：

(3)

参数列为

(4)

计算离散解有

(5)

经逆向推导，由一次累加可还原预测值：

(0)(k)=(1)(k)-(1)(k-1).

(6)

在线实时预测就是用N个原始探测数据建立以上GM(1，1)模型，并预测下一时刻的预测值。而随着探测系统的扫描，得到下一时刻的测量值后，则放弃原数据列中的初值，选取最新测量值，形成新的数据列{x(0)(i)}(i=2，…，N+1)，重新建立GM(1，1)模型，如此进行循环迭代，实现目标航迹的实时预测。

2 灰色预估模型缺陷分析

基于灰色理论的目标航迹预测模型简单，计算简便，但GM(1,1)自身存在不足：

1)背景值邻值权系数μ定义的盲目性[10]。背景值的构造控制是灰色模型预测误差控制的关键，如(4)式中背景值z(1)(k)的构造过程中，一般其邻值权系数μ=0.5，而μ的定义直接影响到发展系数a以及灰作用量b的确定。更进一步，GM(1,1)模型的预测精度则取决发展系数a和灰作用量b，因此背景值邻值权系数μ取值为0.5存在一定的盲目性，不能保证模型预测结果达到最佳。

基于灰色理论的目标跟踪航迹预测模型是微分方程模型，摒弃大量样本的统计特性研究，而是将所有信息统一为灰色过程，通过累加生成弱化序列中数据的随机性，生成规律较强的数列，因此很容易实现少数据、贫资料状况下的目标状态预测。尽管对灰色理论本身缺陷进行了针对性的改进，但一直无法彻底摆脱其局限性，大多在原有基础上尽可能提高灰色模型的拟合精度，那么在基于灰色理论的目标航迹预测中，将研究重心从算法本身转移到误差补偿，不失为一种有效的途径。

3 灰色残差修正模型

在BAT子弹药对地面目标跟踪航迹预测中，弹载跟踪系统的飞行、环境干扰、测量系统误差以及目标的运动状态突变均不能保证原始数据的准确性。那么，在线目标跟踪及航迹更新若仅依赖于传统灰色模型的少数据迭代外推思想，可能造成计算误差累积效应，最终导致目标跟踪失败。针对该问题，本文采取的解决方案是在灰色理论的基础上引入残差修正机制，建立标准GRMM和GVRMM用于解决目标跟踪过程中由于算法局限性造成的航迹预测误差累积的问题。

3.1 标准灰色残差修正模型

设第k时刻预测值与原始累加值的残差为

(7)

得到一次修正估计值：

(8)

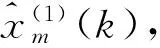
(9)

可得

(10)

11月7日，丽江和迪庆供电局应急指挥中心就已布置完毕，启动了24小时应急值班制。两个供电局分别与当地水务部门建立了联动机制，安排专人实时获取水文信息，及时开展险情分析研判工作。

建立n次累加m次GRMM：

(11)

(12)

可得

(13)

设残差参数列为

(14)

辨识算式为

Δm(n)=
[Δ(A⋮B),Δ(A⋮B)]-1Δ(A⋮B)y(Δ(n-1))，

(15)

得到离散解为

(16)

该模型是一种嵌套式灰色模型，先由灰色模型得到目标航迹预测值序列，进而得出残差序列，再对残差序列进行灰色模型建模计算，与预测值相加得出更加逼近真值的预测结果。因此，GRMM和GM(1，1)模型一样需要同时在线进行，达到目标跟踪及误差实时修正的目的，可有效提升目标跟踪精度。

3.2 灰色Verhulst残差修正模型

GVRMM[13]是灰色模型的改进形式，在解决具有饱和“S”型预测问题时具有良好的效果。通过研究发现[14]，BAT在飞行过程中对地面目标的航迹预测残差在目标的机动动作及其他干扰情况下可以认为具有饱和的近似“S”型序列，那么采用GVRMM对目标航迹预测残差进行建模及修正则显得更加合理。

航迹残差计算如(7)式～(10)式所示，建立n次累加m次GVRMM：

(17)

(18)

可得

(19)

设残差参数列

(20)

辨识算式为

Δm(n)=
[Δ(A⋮B),Δ(A⋮B)]-1Δ(A⋮B)y(Δ(n-1))，

(21)

得到离散解为

(22)

4 计算实例

图1 BAT子弹药对地目标跟踪示意图Fig.1 Schematic diagram of tracking a target by BAT submunition

以BAT子弹药对地面目标跟踪为例，选用BAT子弹药相对目标的径向距离r作为目标跟踪参量，如图1所示，设BAT在空中以100 m/s的速度逼近目标，目标的先以12.5 m/s的速度运动，在某一时刻开始以的3.4 m/s2加速度进行加速运动，弹目初始距离330 m，以每0.1 s的径向距离探测值作为原始数据，选取最初5个数据点(见表1)，首先进行GRMM和GVRMM建模和一步预测。

表1 BAT子弹药对地目标径向距离原始数据Tab.1 Radial distance between BAT submunition and target

将表1数据带入文献[8]所提的传统GM(1,1)模型得

(1)(k)=-11 343.081 7e-0.028 796(k-1)+
11 673.0817，k≥1.

经过2次累加1次残差修正的GRMM模型为

(1)(k)=0.199 0e-0.752 9(k-1)-0.199 0，k≥1.

经过2次累加1次残差修正的GVRMM模型为

(1)(k)=0.635 6e-0.635 633(k-1)，k≥1.

当弹载测距装置测得k=6时的弹目径向距离为286.321 4 m时，抛去原数据列中首值，重新建立航迹预估模型及残差修正模型，得到GM(1,1)模型为

(1)(k)=-8 718.388 9e-0.032 392(k-1)+9 004.710 3，
k≥1.

经2次累加1次残差修正的GRMM模型为

(1)(k)=0.035 3e-0.436 633(k-2)-0.035 3，k≥2.

2次累加1次残差修正的GVRMM模型为

(1)(k)=0.714 4e-0.714 360(k-2)，k≥2.

再由(10)式即可得到经m次残差修正后的1次累加预测值。

定义残差均值为

(23)

由表1数据计算得到：基于传统GM(1,1)径向距离预测误差为0.145 1 m，误差方差为0.034 4 m2；而GRMM径向距离预测误差为0.123 9 m，误差方差为0.010 1 m2；GVRMM径向距离预测误差为0.061 9 m，误差方差为0.028 6 m2. 当弹载测距装置测得k=6时的弹目径向距离为286.321 4 m时，新数据列计算结果为：基于GM(1,1)径向距离预测误差为0.138 3 m，误差方差为0.023 6 m2；而GRMM径向距离预测误差为0.131 4 m，误差方差为0.011 3 m2；GVRMM径向距离预测误差为0.058 3 m，误差方差为0.029 2 m2.

定义相对偏差百分比(RPE)为

(24)

定义平均相对偏差比(ARPE)为

(25)

再对目标进行全局在线观测及航迹预测，总观测时长为1 000 ms，采样频率为100 Hz，分别建立基于GRMM和GVRMM的全局航迹预测模型并计算预测结果。图2给出了两种灰色预估模型的估计值以及文献[8]所提GM(1，1)的估计值，图3为260～320 ms的局部放大图。从图2中可以清楚地看到，GVRMM的航迹值最接近真实值，其次为GRMM模型预估值，而非修正GM(1，1)模型预测结果的相对其他两种模型的预估结果较差。

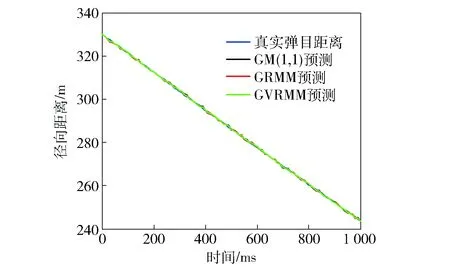
图2 真实弹目距离及不同模型预测结果Fig.2 Real projectile-target distances and predicted results of different models

图3 260～320 ms时的真实弹目距离及不同模型预测结果Fig.3 Real projectile-target distances data and predicted results of different models in the time range from 260 to 320 ms

图4显示了不同模型全局在线预测的相对偏差，从图4中不难发现：GM(1，1)航迹预测模型的偏差较大，且波动幅度较大；GRMM和GVRMM预测偏差均较小，而GVRMM偏差最小。图5和图6给出了3种模型预测值的最小均方误差和相对偏差比RPE曲线，可以发现，灰色残差修正航迹预测模型的误差要明显小于未修正灰色航迹预估模型。

图4 目标航迹预测偏差Fig.4 Predicted track errors of different models

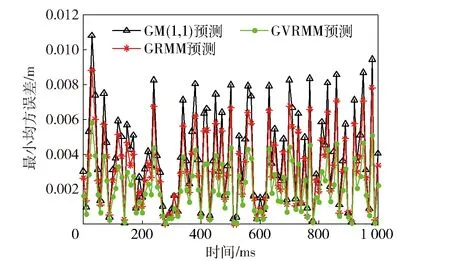
图5 目标航迹预测均方误差Fig.5 MSEs of predicted target tracks

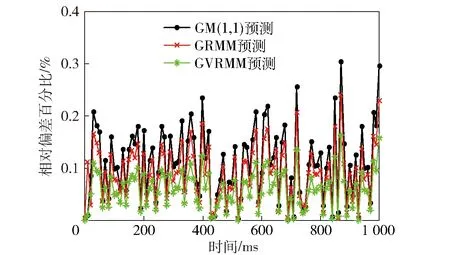
图6 目标航迹预测相对偏差百分比Fig.6 RPEs of predicted target tracks of different models

计算3种模型所对应的ARPE(见表2)分别为：0.121 1、0.089 9和0.059 1. 由此验证了基于灰色残差修正理论的目标航迹预测精度优于未修正模型航迹预测精度，其中GVRMM精度最优。值得注意的是，传统GM(1，1)模型耗时最短为0.156 s，而本文所提的GRMM模型与GVRMM模型耗时分别为0.228 s和0.226 s，原因在于GRMM和GVRMM计算过程中在GM(1，1)的基础上额外增加了残差预估和修正，从而计算复杂度上增加了两次累加过程，但每次迭代时间远小于传感器测量一次的时间，因此认为本文所提两种算法仍然符合BAT子弹药对地目标跟踪的实时性要求。

表2 3种模型全局预测性能对比Tab.2 Comparison of prediction performances of three models

5 结论

针对BAT子弹药对目标航迹预测的精度问题，提出了两种灰色残差修正的目标航迹预测方法。通过与传统灰色航迹预估模型对比，本文所提的两种残差修正模型的航迹预测精度分别提高3.12%和6.2%，而基于灰色Verhulst估计的GVRMM航迹预测性能最优。

本文主要以弹目径向距离为例进行了算法仿真计算，而真实探测系统还会涉及弹目方位角和俯仰角等其他参数，则多参数的灰色系统目标跟踪算法将是下一步工作重点。

References)

[1] Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35-45.

[2] Hlinomaz P, Hong L. A multi-rate multiple model track-before-detect particle filter[J]. Mathematical and Computer Modeling, 2008, 49(1): 146-162.

[3] Lan J, Li X R. Equivalent model augmentation for variable structure multiple-model estimation[J]. IEEE Transactions on Aerospace and Electronic System, 2013, 49(4): 2615-2630.

[4] 孙宝亮, 姜春兰, 李明, 等. 基于模糊逻辑的交互式多模型网络化弹药多节点目标跟踪算法[J]. 兵工学报, 2015, 36(4):595-601. SUN Bao-liang, JIANG Chun-lan, LI Ming, et al. Fuzzy logic-based interacting multiple model algorithm of networked munitions for target tracking[J]. Acta Armamentarii, 2015, 36(4):595-601. (in Chinese)

[5] Kayacan E, Ulutas B, Kaynak O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784-1789.

[6] Kumar U, Jain V K. Time series models (Grey-Markov, Grey model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India[J]. Energy, 2010, 35(4):1709-1716.

[7] 赵建忠, 叶文, 张磊. 基于数据融合和改进新陈代谢不等间距GM(1,1)模型的导弹装备故障预测[J]. 兵工学报, 2014, 35(10): 1689-1695. ZHAO Jian-zhong, YE Wen, ZHANG Lei. Failure prediction of missile equipment based on data fusion and AMUGM(1,1) model[J]. Acta Armamentarii, 2014, 35(10): 1689-1695. (in Chinese)

[8] 顾晓辉, 王晓鸣, 赵有守. 基于灰色系统预测直升机航迹的研究[J]. 航空学报, 2001, 22(6): 559-562. GU Xiao-hui, WANG Xiao-ming, ZHAO You-shou. Prediction of helicopter tracks based on grey system theory [J]. Acta Aeronautica et Asstronaytica Sineca, 2001, 22(6):559-562. (in Chinese)

[9] Xu J, Tan T, Tu M, et al. Improvement of grey models by least squares[J]. Expert Systems with Applications, 2011, 38(11):13961-13966.

[10] 罗党, 刘思峰, 党耀国. 灰色模型GM(1,1)优化[J]. 中国工程科学, 2003, 5(8):50-53. LUO Dang, LIU Si-feng, DANG Yao-guo. The optimization of grey model GM(1,1)[J]. Engineering Science, 2003, 5(8):50-53. (in Chinese)

[11] 何海, 陈绵云. GM(1, 1)模型预测公式的缺陷及其改进[J]. 武汉理工大学学报, 2004, 26(7): 81-83. HE Hai, CHEN Mian-yun. Prediction formula’s defect of GM(1,1) and its improvement[J]. Journal of Wuhan University of Technology, 2004, 26(7): 81-83. (in Chinese)

[12] 宁小磊, 吴颖霞, 于天朋,等. 基于改进灰色关联分析的仿真模型综合验证方法[J]. 兵工学报, 2016, 37(2):338-347. NING Xiao-lei, WU Ying-xia, YU Tian-peng, et al. Research on comprehensive validation of simulation models based on improved grey relational analysis [J]. Acta Armamentarii, 2016, 37(2):338-347. (in Chinese)

[13] 崔立志, 刘思峰, 李智屏.灰色离散Verhulst模型[J]. 系统工程与电子技术, 2011, 33(3): 590-593. CUI Li-zhi, LIU Si-feng, LI Zhi-ping. Grey discrete Verhulst model[J]. Systems Engineering and Electronics, 2011, 33(3): 590-593. (in Chinese)

[14] 刘亚雷.三维运动声阵列对声目标跟踪理论研究[D]. 南京:南京理工大学, 2013. LIU Ya-lei. Study on the tracking theory of 3D dynamic acoustic array for acoustic target[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese)

Target Track Prediction Method Based on Grey Residual Modification Theory

DI Yi1， GU Xiao-hui1， LONG Fei2

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.Institute of Intelligent Information Processing, Guizhou University, Guiyang 550025, Guizhou, China)

Two grey residual modification models are proposed for the track prediction precision of brainpower antitank (BAT) submunition based on grey theory, which are grey residual modification model (GRMM) and grey Verhulst residual modification model (GVRMM). A grey model of target track prediction is established, and the limitations of this model are analyzed. GRMM and GVRMM are used to correct the grey forecast model on line, respectively. It shows that the proposed method based on real-time residual modification mechanism can be used to reduce the prediction error effectively, and GVRMM has better efficiency in improving track prediction precision.

ordnance science and technology; target tracking; track prediction; residual modification; grey residual modification model

2016-05-03

国家自然科学基金项目(61263005)

邸忆(1987—), 男, 博士研究生。E-mail: diyi8710@163.com

顾晓辉(1964—), 男, 教授，博士生导师。E-mail: gxiaohui@njust.edu.cn

TJ413+.3

A

1000-1093(2017)03-0454-06

10.3969/j.issn.1000-1093.2017.03.006