不同初始场及其扰动对WRF模拟暴雨的影响

袁有林，杨秀洪，杨必华，赵军，周开鹏，张广兴

（1.中国人民解放军63610部队，新疆 库尔勒 841001；2.中国气象局乌鲁木齐沙漠气象研究所，新疆 乌鲁木齐 830002；3.中亚大气科学研究中心，新疆 乌鲁木齐 830002）

不同初始场及其扰动对WRF模拟暴雨的影响

袁有林1，杨秀洪1，杨必华1，赵军1，周开鹏1，张广兴2，3

（1.中国人民解放军63610部队，新疆 库尔勒 841001；2.中国气象局乌鲁木齐沙漠气象研究所，新疆 乌鲁木齐 830002；3.中亚大气科学研究中心，新疆 乌鲁木齐 830002）

使用ERA-interim和FNL再分析资料分别驱动WRF，对2013年7月12—13日的一次暴雨过程进行数值模拟，详细比较了WRF模拟结果之间的差异。结果表明：（1）两种资料在次天气尺度上存在着较大差异，并由此造成了模拟结果之间的差异，ERA-interim作为初始场对降水的模拟优于FNL资料，反映了WRF对初、边界条件的敏感性；（2）从区域总降水量来看，湿度场扰动对降水量的影响最大，其次是风场扰动和温度场扰动，最小的是侧边界扰动；（3）从降水误差来看，湿度场扰动引起的降水误差最大，在积分20 h内风场扰动的降水误差大于温度场，积分21～24 h则相反，侧边界扰动引起的降水误差在前期比较小且增长缓慢，积分一段时间之后与单个气象要素扰动引起的降水误差相当。

WRF；暴雨；初始场；初值扰动；侧边界扰动

数值预报是在给定的初始和边界条件下，对描述大气运动的物理方程组进行数值求解，预报未来某个时刻的大气运动状态，可见数值预报也成为一种典型的初值问题。Lorenz[1]指出初始场的微小误差随着模式积分时间的增长也会对预报结果产生较大影响。由于人为的、仪器的、观测网络覆盖率及同化和客观分析方法的影响，初始场总会存在着误差[2]，并且地球上的大气在特殊地形以外不存在水平上的边界，而区域模式却假定大气是有边界的[3]，我们得到的模式初始场及边界条件只能是大气真实状态的近似，因此初、边界条件能否真实反映大气的运动状态，能否与模式匹配协调，直接影响到模式的预报结果的好坏[4-8]。

目前主要使用高分辨率的区域中尺度模式对暴雨等极端天气进行预报[9-11]，这必然面临初始场和边界条件问题。国内外已有许多专家从不同角度对这一问题做过研究[12-16]。龚建东等[17]研究指出，区域中尺度模式模拟误差除了来源于初始误差外，模式误差、侧边界条件的影响也同样重要。Zhang[18]比较全面地研究了中尺度暴雨的可预报性，表明模式和初始场误差对预报结果有显著影响。贝耐芳等[19]用数值模式研究了“98·7”长江流域暴雨，指出该暴雨过程的数值预报对初始场很敏感，初始信息是否完全是这次暴雨预报成功与否的关键。孔荣等[20]用GARPES-Meso对湖南一次大暴雨过程进行了数值试验，指出模拟降水出现过早主要是由模式初值误差引起的。朱红芳等[21]用T213和FNL资料分别驱动GRAPES模式，对淮河流域的一次暴雨过程进行了数值试验，表明模式的预报能力对不同初始场和侧边界条件存在不同程度的依赖性。麻素红等[22]利用T213和T106提供的初始场和侧边界条件对台风路径进行了数值预报，表明初始场和侧边界的改进可以明显提高台风路径数值预报能力。闫敬华[23]对华南地区的一次降水过程进行了研究表明，由于侧边界信息迅速向模式内传播，初值仅显著影响中尺度模式大约前10 h的预报，以后的预报趋势主要决定于边界信息。朱本璐等[24]用AREM模式对华南一次暴雨过程进行了模拟，表明初始时刻不同物理量场加实际振幅的正态分布随机扰动时，对降水的影响是不同的。这些研究都为提高区域中尺度模式的预报能力提供了有价值的参考依据。

本文用WRF V3.6模式对2013年7月12日08时—13日08时（北京时，下同）发生在陕晋冀鲁地区的暴雨过程进行个例试验，分析ERA-interim和FNL再分析资料间的差异，并比较了这两种资料对WRF模拟结果的影响，最后研究初始温度场、风场、湿度场及侧边界扰动对降水模拟的影响特征及其差异，希望能为改进区域模式的初始条件、边界条件和提高数值模式对暴雨等极端天气过程的模拟能力提供参考。

1 天气过程概况

从500 hPa天气图上看（图1a），12日08时巴尔喀什湖北部为脊、南部为槽，贝加尔湖附近有一低压槽，内蒙古北部为弱脊，东北在高压控制下，甘肃以东有短波槽活动，即以45°N为界槽和脊呈反位相分布。40°N以南我国大部分地区被584线控制，副高588线的西脊点位于（30°N，111.6°E），到12日20时移至（32°N，112.7°E），表现为东退北抬。700 hPa天气图上（图1b），12日08时在甘陕宁交界、晋冀鲁附近有明显的风切变，并且沿着312线有一致的西南气流，风速为4～12 m/s，为暴雨区提供了充足的水汽和不稳定能量。据此可知，西风槽携带的冷空气和沿着副高外侧输送来的暖湿气流于陕西、山西、河北、山东上空交汇，并且低层存在明显的切变线配合，这些系统的共同作用给以上地区带来强降水天气。

图1 2013年7月12日08时500 hPa（a）和700 hPa（b）天气形势

图2 2013年7月12日08时—13日08时24 h累积降水实况（a.单位:mm）和嵌套区域（b）

2013年7月12日08时—13日08时，陕西中部、山西中南部、河北南部和山东北部等地出现了强度较大的降雨过程。图2a是352个站点的降水实况，发生暴雨（>50 mm）的台站有43个，大暴雨（>100 mm）的有4个，山东周村的24 h降雨最多，达到131 mm。此次降水过程雨量大、范围广，是一次典型的暴雨过程。

2 模式设计与再分析资料简介

本文采用WRF V3.6，选用的物理方案主要包括WSM3微物理方案，RRTM长波辐射方案，Dudhia短波辐射方案，YSU边界层方案，Betts-Miller-Janjic积云对流参数化方案，NOAH陆面过程方案，MM5 Monin-Obukhov近地层方案。模拟区域设置如图2b所示，采用双向两层嵌套方案，中心位置为（115°E，34°N），水平网格距分别为30 km和10 km，格点数分别为110×100和166×106，垂直分为31层，模式层顶为50 hPa。为反映实际下垫面状况，采用MODIS下垫面资料，两层嵌套分别采用分辨率为2 m和30 s地形数据。积分时间从2013年7月12日08时—13日08时，共积分24 h，两层网格的积分步长分别为180 s和60 s，1 h输出一次模拟结果。本文使用两种再分析资料驱动WRF，分别为：

（1）ERA-interim（以下简称“ERA”），是欧洲中期数值预报中心ECMWF提供的再分析数据，本文所用数据的水平分辨率为0.75°×0.75°，时间分辨率为6 h，垂直分为37层（1000～1 hPa）。

（2）NCEP FNL是美国国家环境预报中心制作的全球再分析资料，水平分辨率为1°×1°，时间分辨率为6 h，垂直分为26层（1000～10 hPa）。

3 ERA-interim和FNL资料之间的差异

首先对ERA-interim和FNL资料进行比较分析，采用相关系数（式1）来描述两个资料间的相近程度，初值中各格点的值分别为xi、yi，所有格点的平均值用来表示，相关系数越大表示两种资料越相近，差异越小。图3a是两个资料中各气压层位势高度场、温度场和湿度场的相关系数，ERA-interim与FNL资料中位势高度场和温度场700 hPa以上的相关系数超过了0.9，表明相似程度较高；而700 hPa以下相关系数较低，且700 hPa以下位势高度场相关性高于温度场；而湿度场只在550～400 hPa的相关系数大于0.9，并且700 hPa以上高度的相关性最小，表明中高层湿度场的差异较大。

图3 ERA-interim与FNL各层高度场之间、温度场之间和湿度场之间的初始场、大尺度场（a）和扰动场（b）的相关系数

为了便于比较，本文把ERA-interim资料的分辨率处理成1°×1°，之后利用9点平滑滤波公式（式2）对这两种资料进行尺度滤波，滤波公式中的平滑系数为0.5，平滑3次。滤波后波长小于4（为网格距，本文为1°，大约为100 km）的波将衰减98%以上，而波长大于16的波将保留80%以上，所以通过滤波就得到了ERA-interim和FNL的大尺度场，用原始资料减去大尺度场就可以获得扰动场，即次天气尺度。利用滤波的结果可知，就不同气压上的位势高度相关性、温度相关性和湿度相关性而言，大尺度场好于原始资料（图3a），位势高度大尺度场的相关系数在0.93以上，说明两个资料大的环流形势差异很小。但两种资料间的扰动场相关系数较小（图3b），尤其在250 hPa以上高度相关系数迅速变小。总体来看，位势高度扰动场的相关性好于温度扰动场，湿度扰动场的相关性在350 hPa以下好于温度扰动场，而在350 hPa以上的相关性最差。位势高度扰动场、温度扰动场和湿度扰动场的相关系数分别为0.18～0.83、0.14～0.76和-0.12～0.61，说明两种资料初始扰动场之间的差异明显，也就是说扰动场所反映出的次天气尺度有着较大差异，而这种差异也许是影响WRF模式预报能力的一个原因。

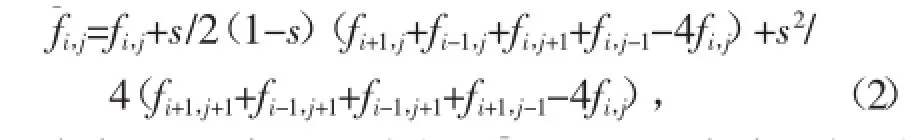
式中fi，j是实况要素场，是平滑滤波后得到的大尺度场，S是平滑系数。

4 不同初始场对WRF模拟结果的影响

本节分别使用ERA-interim和FNL再分析资料驱动WRF模式（分别记为exp_ERA和exp_FNL试验），分析不同初始场对WRF模拟结果的影响，如不作特别说明，以下均是分析d02内的数据。

4.1 高度场、温度场之间的差异

本文分别计算了两个试验850 hPa位势高度场之间和温度场之间的相关系数（图4），以便分析exp_ERA与exp_FNL模拟结果的相似程度。由图可见，在整个模拟时段两试验的850 hPa位势高度场之间和温度场之间的相关系数均大于0.9，表明两种资料模拟的大尺度环流形势有着很好的一致性，位势高度场之间的相关系数随积分时间先增大后减小，温度场之间的相关系数则一直是波动减小，说明模拟结果随积分时间的增加差异逐渐增大。

图4 2013年7月12日08时—13日08时两试验的850 hPa高度场、温度场之间的相关系数

为更明确揭示不同初值对WRF模拟结果的影响，本文参考朱红芳[21]等文章中的离散度公式：

其中FERA、FFNL分别为ERA-interim和FNL作为WRF初值模拟的结果，N是模拟区域总格点数。离散度考虑了FERA、FFNL两个预报结果中所有格点的数据差异大小，用全部格点数据差值求和来代表两个预报场的差距，dxy越小两个场的差异越小。图5给出了两试验的不同气压层（850、500、150 hPa）上温度、位势高度的离散度随时间变化，可知在积分时间内初值引起的差异都是存在的，这种差异尤其温度场的差异（图5a）还会随时间增大，并且温度场低层（850 hPa）差异最大。位势高度场差异（图5b）表现为：低层（850 hPa）离散度前期增大后期减小，高层（150 hPa）前期减小后期增大。两个模拟结果中各个气压上比湿场的离散度（图略）和温度场较为一致，表现为低层比高层的离散度大。

图5 2013年7月12日08时—13日08时两试验不同气压层上温度与位势高度的离散度

4.2 大气总能量的差异

在大气中各种尺度的天气系统的演变过程总是伴随着能量的变化，单位质量的空气有着内能、动能、潜热能和位能4种能量形式，总能量就是把这4种能量相加，用摄氏度表示的总能量的公式[21]如下：

公式中Tt是总能量，t是某气压层的大气温度，z是位势高度，cpd是干空气的定压比热，L是水汽的凝结或水的蒸发潜热，q是比湿，V是风速，A代表空气质量，此式是对单位质量空气而言的，因此A取1 kg。本文提取出模拟结果中850 hPa气压层的温度、比湿、风uv分量和位势高度，用上式求取d02内某一气压上全部格点的Tt，然后对全部的格点求平均值，即可得到等压面上所有积分时间的大气总能量。图6是7月12日08时—13日08时两试验的850 hPa大气总能量的变化，在积分时间内2个初始场驱动WRF模拟的变化趋势一致但数值不同，说明初始场对模拟结果影响较大，且这种差异24 h内不会随积分时间增加而消失。

4.3 降水模拟的差异

从图2a降水实况分布图可以看出，降水主要分布在35.5°N～37.5°N范围内，雨带呈东西向分布，exp_ERA模拟的降雨范围（图7a）与观测值最为接近，而exp_FNL的雨带呈西南—东北向（图7b），与实况差异较大。两个试验模拟的降水差别主要体现在陕晋鲁地区，exp_FNL试验模拟的陕西中北部降水偏小，山西雨区模拟偏南，山东10 mm以上的降雨面积大于试验exp_ERA。从24 h累积雨量来看，试验exp_ERA比exp_FNL雨量多出20.8%，exp_ ERA的最大降水中心位于山东半岛（180 mm），而exp_FNL最强的降水中心在山西东南部（270 mm）。因此，两个试验无论是降水落区、强度还是累积雨量都有着明显的差异。

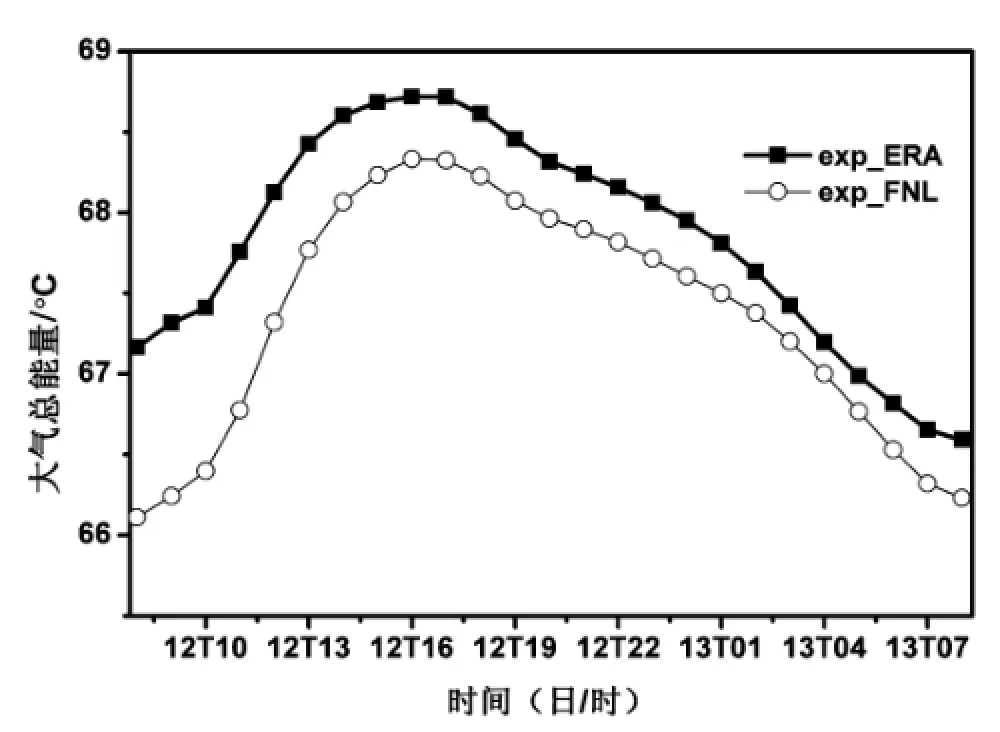
图6 2013年7月12日08时—13日08时两试验的850 hPa大气总能量的变化（单位:℃）

为了进一步分析两者的降水差异，本文比较了2个试验模拟的区域平均（33°～38°N，108°～123°E）逐时降水量演变（图8），可以看出，exp_ERA和exp_FNL模拟的逐时雨量变化趋势基本一致，主要为网格尺度降水，次网格尺度降水只对雨量起调节作用。exp_ERA比exp_FNL模拟的降水量偏大，这主要是由网格尺度降水引起的，说明网格尺度降水对初、边界条件更加敏感。因为降水差异是在选取了相同模式相同参数化方案的情况下发生的，所以这种差异主要是由初、边界条件决定的。

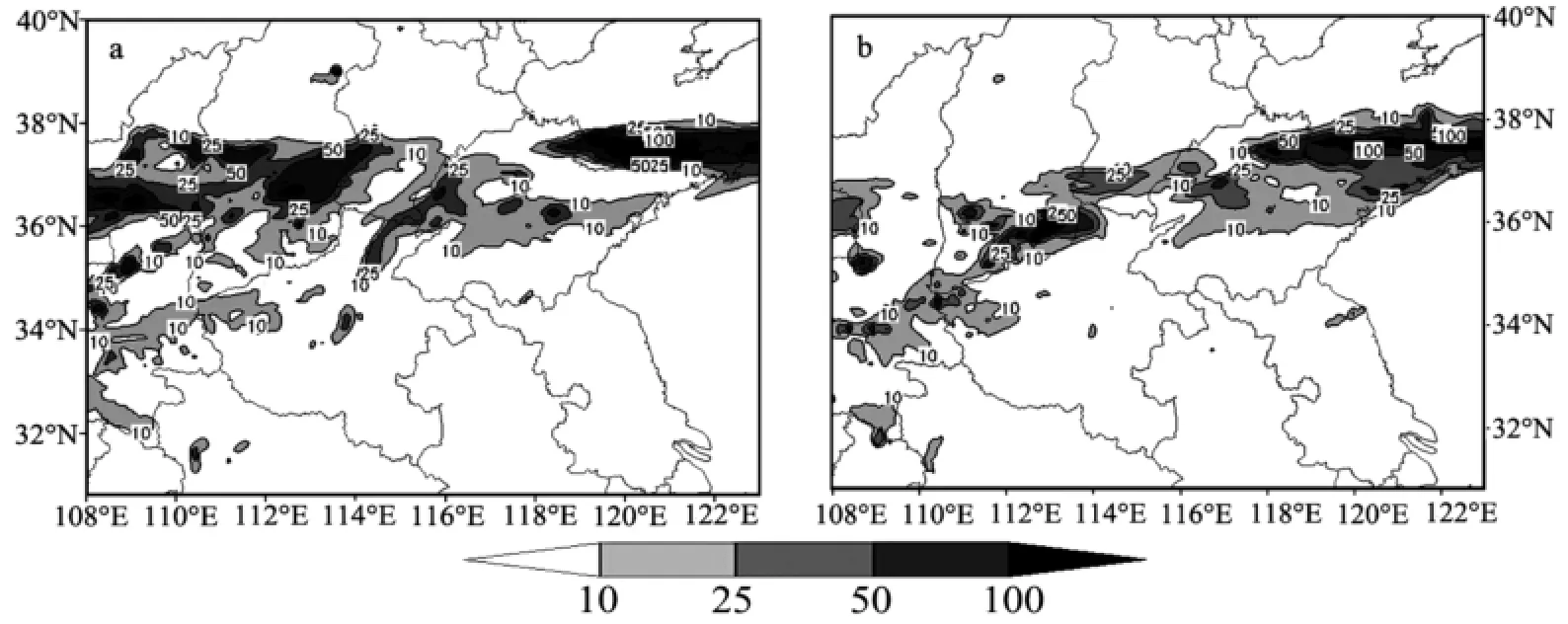
图7 7月12日08时—13日08时模拟的24 h累积降水量/mm

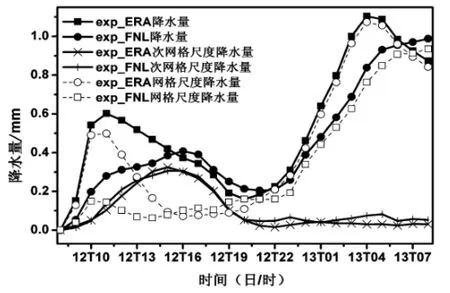
图8 7月12日08时—13日08时模拟区域（33°～38°N，108°～123°E）平均的逐时次网格和网格尺度降水随时间演变（单位：mm）

为了客观反映模式的降水预报水平，用公式5对两组试验的降水预报进行TS评分：

其中预报正确的格点数为NA，空报的格点数为NB，漏报的格点数为NC。TS值的范围为0～1，TS值越大表示预报效果越好。具体的评分方法是将模拟区域d02内的352个气象站的24 h降水实况作为参考标准，把预报场的格点值插值到站点上，对两者进行比较。24 h内把降水分为小雨（0.1～9.9 mm）、中雨（10～24.9 mm）、大雨（25～49.9 mm）和暴雨（50 mm以上）。结果表明：对于各降水等级的评分（表1），试验exp_ERA都高于exp_FNL，所以对本次暴雨过程来说，exp_ERA模拟结果优于exp_FNL。

5 对exp_ERA初值中的物理量场进行扰动

上述研究表明exp_ERA的模拟效果好于exp_FNL，因此本文把exp_ERA作为控制试验，对扰动试验和exp_ERA之间的结果差异进行分析，研究温、湿、风和侧边界误差对WRF模拟暴雨的影响。初值误差可以认为是控制试验exp_ERA初值上加减一个小扰动，模拟误差就是扰动试验与exp_ERA模拟值之差。物理量场扰动的试验设计见表2，试验exp_T是把试验exp_ERA初值中的温度场用exp_FNL温度场代替，相当于exp_FNL与exp_ERA初值中的温度作差得到温度场小扰动，再把温度场小扰动叠加在exp_ERA初值上，这种在气象要素场上加减小扰动不会使初值中不同气象要素场间的平衡状态受到破坏[25]，因而是可行的。试验exp_Q、exp_UV和exp_BDY与试验exp_T的方法是一致的，只是替换的变量不同。通过上述方法可以得到3个新的初值和1个新的侧边界值。

表1 降水TS评分

5.1 不同气象要素扰动对降水的影响

图9是模拟的24 h累积降雨，与控制试验（图7a）对比分析，扰动试验模拟的降水落区差异较小，但降水量的大小和降水中心的分布存在着较大差异。温度场加扰动后（图9a），陕西、山西50 mm和山东北部100 mm以上降水范围减小。湿度场加扰动后（图9b），陕西和冀豫鲁三省交界处的25 mm以上降水范围减小，山东北部50 mm以上降水范围减小而100 mm以上增加。风场加扰动后（图9c），模拟区域25 mm以上降水范围增大，山东北部降水情况同湿度场扰动。侧边界扰动后（图9d），陕西10 mm、山西50 mm降水范围减小，降水区域的100 mm降水范围均增大。

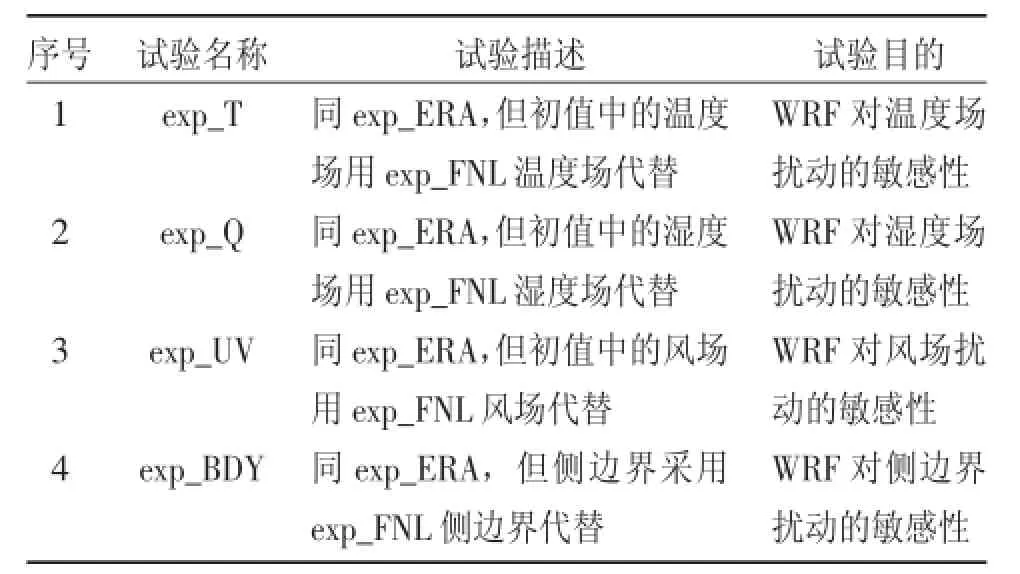
表2 试验方案设计

研究区域（33°～38°N，108°～123°E）内的降水，同控制试验相比，温度场、湿度场、侧边界扰动导致降水量分别减少5.65%、21.02%、1.04%，而风场扰动导致降水量增加6.85%。这就说明湿度场扰动对降水量的影响最大，其次是风场扰动、温度场扰动，而侧边界扰动的影响最小。

降水误差是扰动试验和控制试验模拟的降水量之间的均方根误差，按下式计算:

式中N表示台站总数，Mi为扰动试验第i站的降水，Oi为控制试验第i站降水。通过降水均方根误差的分析可知（图10），湿度场扰动引起的降水误差最大；在积分20 h内风场扰动的降水误差大于温度场，积分21～24 h则相反；而侧边界扰动的降水误差在前期增长比较缓慢，积分8 h后增长速度变快，13 h后接近于温度场扰动引起的降水误差，24 h后超过了风场扰动引起的降水误差，可见侧边界扰动从边界向中间传播，对降水的影响逐渐增大，在积分一定时间之后，其与单个气象要素扰动引起的降水误差相当。

5.2 扰动试验与控制试验的温湿风相关系数演变

从温度相关系数（图11a）可以看出，温度场扰动试验exp_T与控制试验模拟的温度相关系数在积分时间内均小于1，表现为先增大后减小；而exp_Q、exp_UV、exp_BDY与控制试验模拟的温度相关系数仅仅在初始时刻为1，其它时刻均小于1，并且在24 h内相关系数总体上是减小的，表明湿度、风场和侧边界扰动后，引起了温度场的扰动。由图11b、c、d可以看出，温度场扰动同样引起了风场u、v和湿度场的扰动，其它物理量场扰动也有同样的结论，表明扰动初值中的某一变量，模式通过一段时间积分后，就会引起其他物理量的扰动，也就是说当初始场中某一个物理量存在误差时，在模式积分过程中就会导致其它物理量也出现误差，反映了模式中物理量间的相关性。

从扰动试验和控制试验的相关系数可以看出，扰动湿度场在积分20 h内对其它变量影响最大，可以使其它变量场（温、风场）的扰动较快发展；侧边界扰动后温度场、风场的相关系数最大，因而侧边界扰动对温度场、风场影响最小，在积分14 h前对湿度的影响也是最小的，而14 h后侧边界扰动对湿度的影响大于对温度场扰动的影响。

图9 2013年7月12日08时—13日08时24 h累积降水量/mm

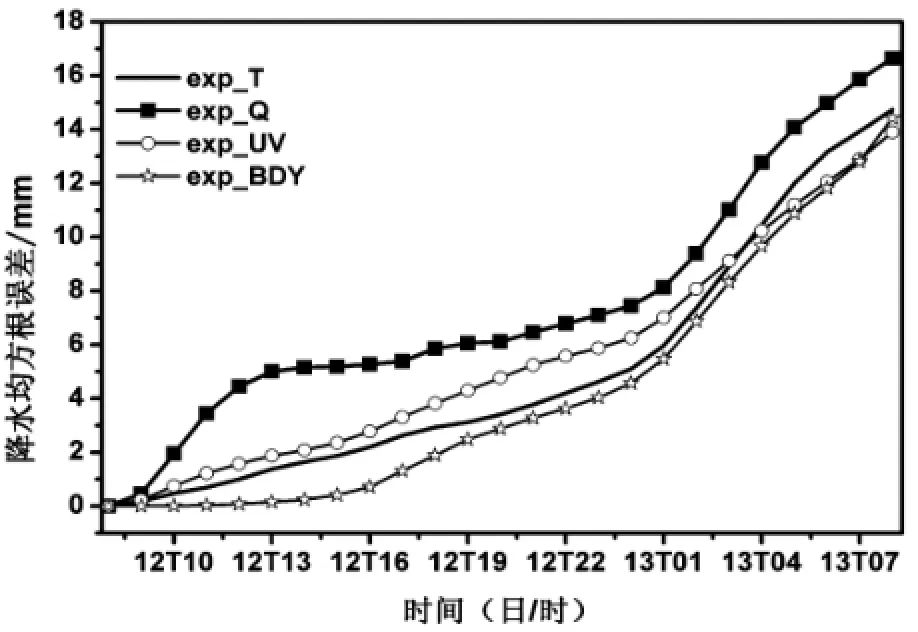
图10 4个试验降水均方根误差随时间演变/mm

在温度场上叠加小扰动会对大气中的温度梯度产生微小的影响，也会影响到大气容纳的水汽多寡；在风场上叠加小扰动会影响到大气的辐合辐散，进而影响大气的对流强弱；在湿度场上叠加小扰动后，大气中水汽含量会受到影响；侧边界条件与真实大气之间存在着误差，侧边界扰动从边界向中间传播，对降水的影响逐渐增大。并且，扰动初值中的某一变量，模式通过一段时间积分后，就会引起其他物理量的扰动，这些扰动产生的综合效应就是影响大气中的温度分布、对流强度和水汽含量等物理量场，同时也能影响小尺度涡旋的发生、发展，最终的结果就是改变了降水的强度和分布。

6 结论

本文采用WRF模式，对2013年7月12日08时—13日08时发生在陕晋冀鲁地区的降水过程进行了个例试验，主要结论如下：

（1）通过尺度滤波可知，ERA-interim与FNL再分析资料的大尺度场的相似性较高，差异主要体现在次天气尺度。用这两种资料分别驱动WRF，模拟的各物理量场间存在着较大差异，且这种差异24 h内不会随积分时间增加而消失，反映了WRF对初、边界条件的敏感性。

（2）用ERA-interim资料作为初始场对降水的模拟优于FNL资料作为初始场的模拟。两种资料模拟的逐时雨量的次网格尺度降水量基本是一致的，差异主要体现在网格尺度降水上，表明对本次暴雨过程而言，网格尺度降水对初、边界条件更加敏感。

（3）从区域总降水量来看，湿度场扰动对降水量的影响最大，其次是风场扰动和温度场扰动，侧边界扰动对降水量的影响最小。通过降水均方根误差的分析可知，湿度场扰动引起的降水误差最大；在积分20 h内风场扰动的降水误差大于温度场，在积分21～24 h则相反；侧边界扰动引起的降水误差从边界向中间传播，在前期增长比较缓慢，积分8 h后增长速度加快，积分一段时间后与单个气象要素扰动引起的降水误差相当。

（4）扰动初值中的某一变量，模式通过一段时间积分后，就会引起其他物理量的扰动。扰动湿度场在积分20 h内对温度场和风场的影响最大，侧边界扰动对温度场、风场影响最小，而14 h后侧边界扰动对湿度的影响大于对温度场扰动的影响。

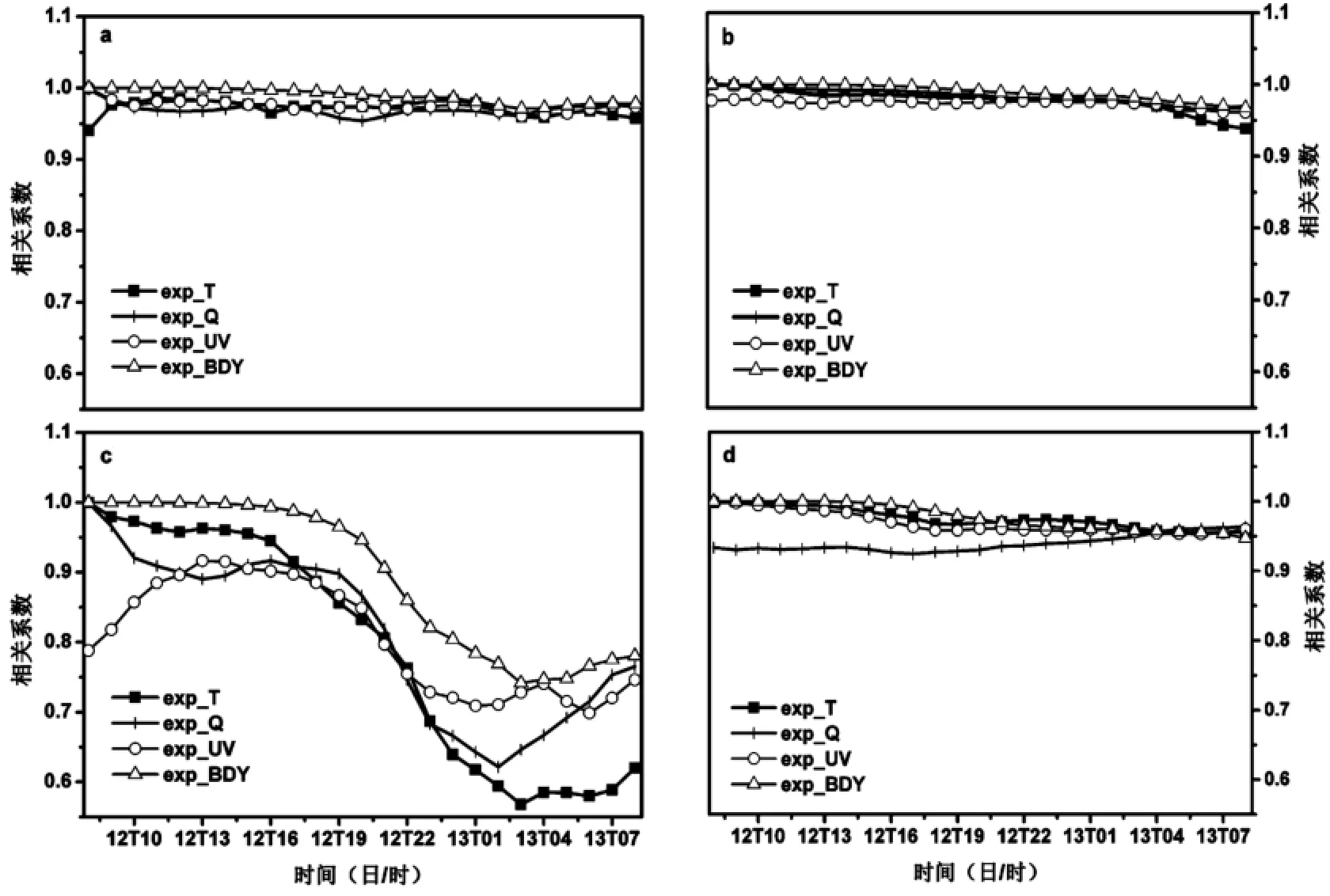
图11 扰动试验与控制试验500 hPa各物理量的相关系数变化

[1] Lorenz E N.Deterministic nonperiodic flow[J] .Journal of the atmospheric sciences，1963，20（2）：130-141.

[2] 王洋，曾新民，葛洪砘，等.陆面特征量初始扰动的敏感性及集合预报试验[J] .气象，2014，40（2）：146-157.

[3] Warner T T,Peterson R A,Treadon R E.A tutorial on lateral boundary conditions as a basic and potentially serious limitation to regional numerical weather prediction [J] .Bulletin of the American Meteorological Society，1997，78（11）：2599-2617.

[4] 彭继达，程兴宏，孙治安，等.两种不同初始场对太阳辐射模拟效果的影响[J] .高原气象，2014，33（5）：1352-1362.

[5] 汤浩，贾丽红.背景场和物理过程对WRF模式在新疆区域预报性能的影响[J] .沙漠与绿洲气象，2014，8（3）：27-33.

[6] 杨袁慧，师春香，王炜，等.一次强降水模拟中土壤湿度初值的影响研究[J] .气象，2013，39（11）：1481-1489.

[7] 汤浩，贾丽红，居来提吾甫尔.新疆区域模式MM5和GRAPES预报能力对比检验[J] .沙漠与绿洲气象，2012，6（1）：21-26.

[8] 岳甫璐，王春明，崔强，等.“7·21”北京大暴雨过程的地形作用分析和数值试验研究[J] .沙漠与绿洲气象，2014，8（2）：41-53.

[9] 马艳，董海鹰，陈尚.WRF中不同湿过程对青岛一次暴雨过程的预报性能检验[J] .干旱气象，2016，34（3）：494-502.

[10] 艾凯，郑益群，陈浩伟.WRF模式中地形重力波参数化方案应用及不同拖曳力试验[J] .干旱气象，2016，34（1）：125-135.

[11] 张钊扬，钱贞成，王春明，等.江苏一次突发暴雨的数值模拟[J] .气象与环境科学，2014，37（3）：67-75.

[12] 张立凤，罗雨.初始场对暴雨数值预报的影响及集合预报试验[J] .气象科学，2010，30（5）：650-656.

[13] 许晓林，徐海明，何金海.初边界条件不确定性对AREM模拟一次华南致洪暴雨的影响[J] .南京气象学院学报，2009，32（2）：196-205.

[14] 陈宇，王小桃，王瀛，等.基于中尺度集合预报的“8·16”抚顺地区特大暴雨过程分析[J] .气象与环境学报，2015，31（6）：1-8.

[15] 袁有林，杨必华，周宏，等.WRF模式不同集合预报方案对一次大范围暴雨过程的模拟研究[J] .干旱气象，2016，34（6）：1027-1036.

[16] 官元红，周广庆，陆其峰，等.大气初始场对短期气候数值预测的影响[J] .大气科学学报，2014，37（5）：631-641.

[17] 龚建东，邱崇践，王强，等.区域四维变分资料同化的数值试验[J] .气象学报，1999，57（2）：131-142.

[18] Zhang F,Odins A M,Nielsen-Gammon J W.Mesoscale predictability of an extreme warm-season precipitation event[J] .Weather and forecasting，2006，21（2）：149-166.

[19] 贝耐芳，赵思雄.初值及物理过程对“98·7”暴雨预报结果的影响[J] .气候与环境研究，2002，7（4）：386-396.

[20] 孔荣，王建捷.一次南方大暴雨过程的数值模拟及其误差的敏感性诊断分析[J] .热带气象学报，2006，22（6）：582-592.

[21] 朱红芳，王东勇，管兆勇，等.不同初始场条件对GRAPES模式数值预报的影响[J] .气象学报，2007，65（4）：493-502.

[22] 麻素红，瞿安祥.不同初始场及侧边界对台风路径数值预报的影响[J] .热带气象学报，2004，20（6）：737-742.

[23] 闫敬华.中尺度数值预报模式初边值作用的试验研究[J] .热带气象学报，2003，19（4）：337-344.

[24] 朱本璐，林万涛，张云.初始扰动对一次华南暴雨预报的影响的研究[J] .大气科学，2009，33（6）：1333-1347.

[25] 罗雨，张立凤.一次梅雨暴雨预报中的误差演变及可预报性分析[J] .气象学报，2010，68（3）：411-420.

Effects of Different Initial Fields and Initial Perturbations on Simulation of a Heavy Rainfall by WRF

YUAN Youlin1，YANG Xiuhong1，YANG Bihua1，ZHAO Jun1，ZHOU Kaipeng1，ZHANG Guangxing2，3
（1.Unit of 63610 of the Chinese People’s Liberation Army，Korla 841001，China；2.Institute of Desert Meteorology，China Meteorological Administration，Urumqi 830002，China；3.Center for Central Asian Atmosphere Science Research，Urumqi 830002，China）

A typical heavy rainfall process occurred during 12-13 July 2013 in the north of China was simulated using the meso-scale model WRF V3.6.Two groups of contrast numerical experiments were conducted to investigate the sensitivity of model prediction results to initial fields provided by the ERA-Interim and FNL data,respectively.The results show that：（1）there is a significant difference between the initial field of the ERA-Interim and FNL data at the subsynoptic scale,thus leading to different simulation results.The simulated precipitation from the ERA-Interim data is better than that of the FNL data.（2）For 24-hour area precipitation forecast, the perturbation in humidity field has the greatest impact on precipitation,closely followed by that is wind and temperature field,the lateral boundary perturbation has the least impact.（3）The root mean square error（RMSE）of precipitation caused by humidity field perturbation is larger than that caused by the other initial perturbations.In the first 20 hours of the integration period,the RMSE of precipitation caused by wind field perturbation is larger than that caused by temperature field perturbation,while the opposite occurs in the integration period of 21～24 h.The precipitation RMSE caused by lateral boundary perturbation is small in the early stage,and the growth is slow. After a period of model integration,the RMSE of precipitation caused by lateral boundary perturbation is equivalent to that caused by the initial field perturbation of single meteorological variables.

WRF；heavy rainfall；initial field；initial perturbation；lateral boundary perturbation

P456.7

B

1002-0799（2017）01-0067-09

10.12057/j.issn.1002-0799.2017.01.009

2016-06-03；

2016-11-14

国家自然科学基金面上项目（41375070和41075050）资助。

袁有林（1987-），男，硕士，主要研究方向为数值模拟。E-mail：908248336@qq.com

张广兴（1963-），男，副研究员，主要从事大气动力学与中尺度气象研究。E-mail：zhanggx@idm.cn

袁有林，杨秀洪，杨必华，等.不同初始场及其扰动对WRF模拟暴雨的影响[J] .沙漠与绿洲气象，2017，11（1）：67-75.