纸浆材桉树人工林生长与收获预估模型研究

李宗俊，莫燕卿，莫晓勇，赵雪丽，刘 萍

(华南农业大学林学与风景园林学院，广州510642)

纸浆材桉树人工林生长与收获预估模型研究

李宗俊，莫燕卿，莫晓勇，赵雪丽，刘 萍

(华南农业大学林学与风景园林学院，广州510642)

以国营雷州林业局纸浆材桉树人工林为研究对象，基于2015年1—2月调查的190块标准地数据，应用SPSS 19.0，ForStat 2.2软件，研究纸浆材桉树人工林生长与收获预估模型。结果表明:密度指数模型为SDI=1.7470No1.0951e－3.7637t0.05－0.1742L; 断面积模型为 G=16.7828L0.1529(1－e－1.0125×10－8SDI－2.1970t)0.5554; 蓄积模型为M=e2.3641+0.0988L－3.0557t－1G0.9126。研究结果可为国营雷州林业局纸浆材桉树人工林生长收获预估、森林成熟龄确定以及森林资源管理提供理论依据。

纸浆材桉树人工林;林分密度指数;生长收获预估

桉树作为速生树种，用途非常广泛。国内许多学者研究了不同区域不同种类的桉树生长收获模型。曾伟生等［1］研究了海南省松类、桉类、木麻黄、相思、橡胶等5个主要树种相对树高曲线模型;梁理勇等［2］探讨分析了国营雷州林业局刚果12号WS无性系桉树人工林蓄积量与胸径、树高、密度的关系;周元满等［3］研究了不同造林密度对桉树无性系生长的影响，并以Richards生长函数拟合不同造林密度条件下桉树无性系林生长预测模型。纵观桉树生长收获模型多只研究了1～2个测树因子之间的相互关系，没有将桉树生长收获预估模型各测树因子纳入模型体系中。鉴于桉树品种多，生长差异大，难以用统一模型来反映其生长过程并用于预测和决策的特点，本文在前人研究基础上，采用应用最广泛、普适性最强的理论模型，研究了桉树地位指数模型、密度指数模型、全林断面积生长模型、全林蓄积生长模型。在生长模型的基础上通过数学变换推导出基于桉树初植密度N0、林分平均年龄t、地位指数L和林分密度指数SDI的收获预估模型。研究结果可以为国营雷州林业局纸浆材桉树人工林生长收获预估、森林成熟龄确定、森林资源管理等提供理论依据。

1 材料与方法

1．1 材料来源

标准地设置在国营雷州林业局的石岭林场和北坡林场。调查对象树种为华桉1号无性系，植苗造林，林龄为1～5a。标准地设置为正方形，面积为0．04hm2(20m×20m)，样地数量190块，样地情况见参考文献［4］。

1．2 研究方法

1．2．1 模型构造方法

1)地位指数模型

采用哑变量的导向曲线法以9类经典理论生长方程为基础模拟了林分优势木平均高HT和林分年龄t的关系，得出Logisitic方程精度最高，合理性最强。在导向曲线的基础上采用相对优势高法导算了地位指数表并反推了地位指数模型［4］。

2)林分密度指数模型

根据Reineke提出的林分密度指数［5］概念，采用多次剔除立木度不足的方法，模拟林分近似完满立木度时的状态。将此时的线性模型看作最接近林分完满立木度时林分株数与平均胸径的关系，线性模型的参数b即为Reineke林分密度指数方程的幂指数b。根据林分密度指数SDI和林分平均年龄t的散点图以及前人的研究经验，将两者的关系看成是S形的曲线，以Korf方程为基础将初植密度N0和地位指数L引入其中，从而构造出形式为SDI－t的林分密度指数模型。

3)断面积生长模型

以Bertalanffy的同化－异化方程为基础［6］，将林分的断面积G和年龄t代入该方程并将地位指数L和林分密度指数SDI引入方程的参数，其中同化反应参数与地位指数L有关，潜在生长率与实际生长率之间的转化率与林分密度指数SDI有关［7］，将两者代入方程通过一系列数学变换从而构造出含SDI和L的断面积生长模型。

4)蓄积生长模型

学者在对蓄积生长模型进行定量研究时提出，蓄积量为年龄倒数的函数。以Schumacher方程为基础，将密度因子引入方程，从而构建了可变密度的林分蓄积生长模型。

5)收获预估模型

在生长模型基础上通过一系列数学变换构造收获预估模型。构造步骤为:先预估林分的密度指数SDI2，用林分未来的密度指数SDI2除以林分现在的密度指数SDI1，通过数学变换构造林分密度指数预测模型;在已知林分未来密度SDI2基础上再预估林分未来断面积G2，用林分未来的断面积G2除以林分现在的断面积G1构造林分断面积预估模型;最后，在已知林分未来断面积G2的基础上预估林分未来蓄积M2，用林分未来的蓄积M2减去现在的蓄积M1构造林分蓄积预估模型，即收获预估模型。

1．2．2 模型检验方法

模型的检验与评价是贯穿建模工作始终的一个连续过程。当建立一个回归方程后，若要知道方程的选型是否正确则需要抽取一套不参加计算模型参数的独立样本，用样本因变量的观测值与样本回归估计值进行一元线性回归，计算线性相关系数r，判断在显著水平α=0．01上两者相关关系是否显著。本文采用系统抽样的方法抽取了样地总数的10%(19块样地)作为检验模型适应性的独立样本，独立样本数据不作为模拟模型的基础数据。

2 结果与分析

2．1 地位指数模型

根据导出地位指数表的相对优势高法，将年龄带入导向曲线模型(HT=18．2053/(1+ 157．0486e－2．1530t))。得到各龄阶树高理论值Hik，将基准年龄(取导向曲线的二阶导数为0的点即拐点时的年龄为基准年龄，计算为2a)代入方程所得到的树高理论值H0k，H0j为地位指数级。调整系数为:K=H0j×100%，H=K×H。反推出的地

jHijjik0k位指数模型为:

2．2 林分密度指数模型拟合结果

2．2．1 Reineke林分密度指数方程林分密度指数公式为:

其中N为现实林分每公顷株数;D0为标准平均胸径(我国一般D0=10cm);D为现实林分平均胸径，采用多次消去剔除立木度不足的方法求解参数b，多次消去剔除过程如表1。

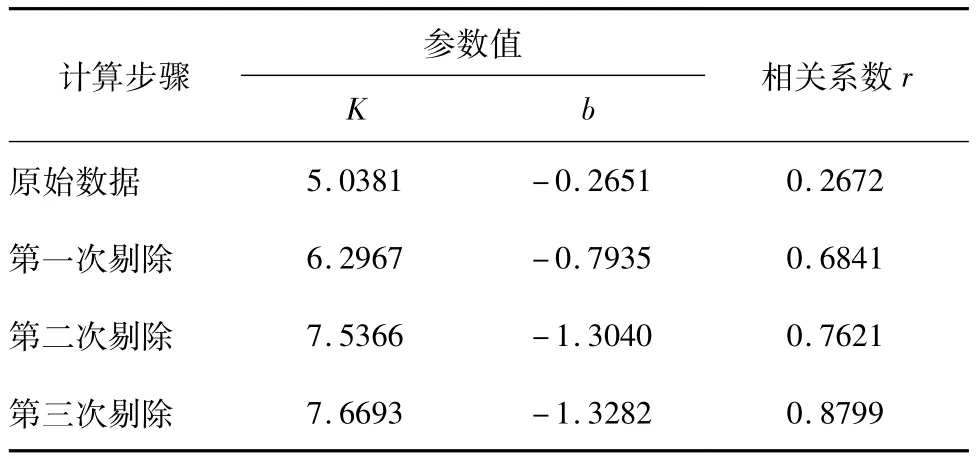
表1 计算过程Tab．1 Computational process

可以看到在经过3次剔除后，参数b的值与赖内克所证明的b=－1．605接近，同时相关系数r= 0．8799，拟合精度较高。该线性模型看作最接近林分完满立木度时林分株数N与平均胸径Dg的关系，即林分的最大密度线(图1)。林分密度指数方程为:

SDI为林分密度指数、N为公顷株数、Dg为林分平均胸径。

2．2．2 林分密度指数模型拟合

有学者研究发现，林分密度指数随着年龄的变化呈现一条近似S形的曲线。根据调查的样地数据，作林分密度指数和年龄的散点图，如图2。观察发现，对于桉树人工林也近似符合这一规律。

图1 近似完满立木度下lnN与ln Dg的线性关系图Fig．1 Linear relationship between lnN and ln Dgunder approximate fully stocking percent

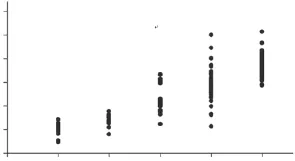
图2 林分密度和年龄的散点图Fig．2 The scatter diagram of stand density and age

本文选取 Korf方程来模拟这一曲线。对于Korf方程，曲线的上渐进参数A与初植密度N0有关，曲线形状与地位指数L有关。初植密度也称为造林密度，表示的是单位面积上的种植点数。在这里引入初植密度是为了在预估桉树未来蓄积收获量时能够分不同初植密度进行比较。本文所研究的桉树人工林为纯林，除非自然灾害和人为干预基本默认不会发生自稀疏的现象，所以在预估蓄积收获量时，林分的初植密度就成了一个不得不考虑的因素。基于此，将初植密度引入林分密度指数模型。模型构造如下:

将式(4)，(5)代入式(3)得到方程:

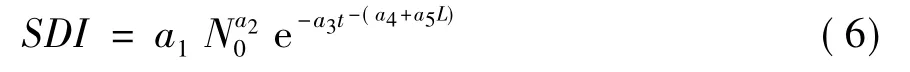
对171块用来模拟模型的样地数据，用一元非线性回归的方法求解模型参数，模型的拟合结果如式(7)。

2．3 断面积生长模型拟合结果

Bertalanffy根据自然界动植物的新陈代谢作用提出了同化－异化方程。其通式为:

根据树木的生长假设，式中α为树木同化系数、β为树木异化系数、m为树木同化作用幂指数。显然，林分断面积生长满足该式，将断面积G和林分年龄t带入式(8)得到如下方程:

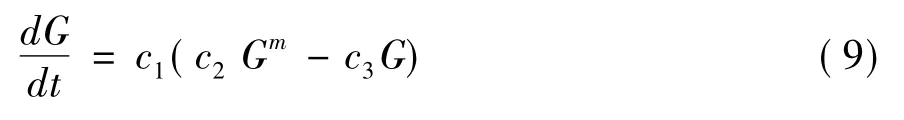
其中同化反应参数c2与地位指数L有关，即c2=a1La2，潜在生长率与实际生长率之间的转化率c1与密度指数SDI有关，即c1=a3SDIa4。断面积模型的推导过程如下:

对式(10)两边同乘(1－m)G－m，得到下式:

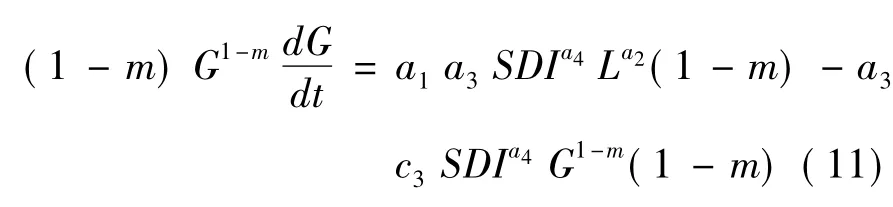
令z=G1－m，得到下式:

式(12)为一阶线性非齐次微分方程，为了计算方便令A=a1a3SDIa4La2，B=a3c3SDIa4，得到:

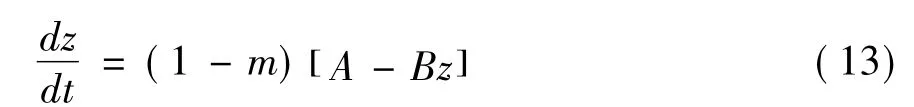
对其进行分离变量:

令C=－A－1e－Bk，将z=G1－m代入式(18)，得到下式:

当t=0时，很显然G=0，即(0，0)为式(20)的一个特解，将其代入式(20)得到:

所以C=－1，将C=－1，A=a1a3SDIa4La2，B=a3c3SDIa4代入式(20)得到下式:

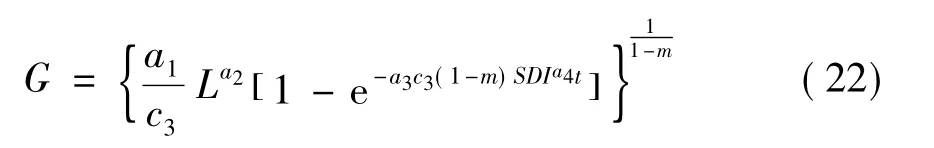
G为林分断面积、L为地位指数、SDI为林分密度指数、t是年龄、b1，b2，b3，b4，b5为模型参数。

对171块用来模拟模型的样地数据，用一元非线性回归的方法求解模型参数，模型的拟合结果如式(24)。

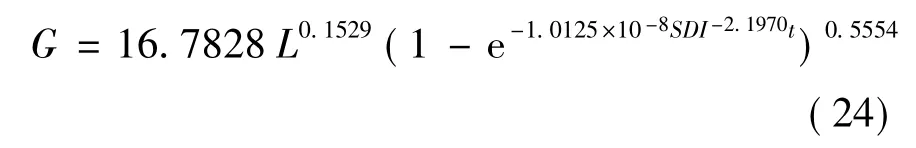
2．4 蓄积生长模型拟合结果

学者在对收获模型进行定量研究时提出，蓄积量为年龄倒数的函数。以Schumacher收获模型为基础，在模型中加入密度因子，从而构建了可变密度的林分收获模型。该模型通式为:

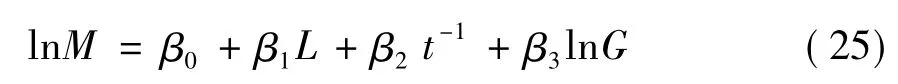
对171块用来模拟模型的样地数据，用一元非线性回归的方法求解模型参数，模型的拟合结果如式(26)。

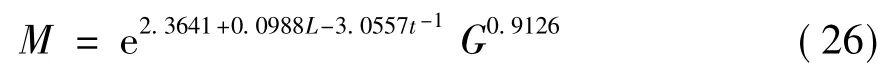
2．5 收获预估模型

现实林分初植密度为N0、地位指数为L、断面积为G1、蓄积为M1，假定林分的初植密度N0与地位指数L不变，据此构造收获预估模型。

根据林分密度指数的模型式(6)，预估未来林分的林分密度指数SDI2，SDI2/SDI1得到:

根据断面积模型式(23)，在已知林分未来的林分密度指数SDI2的情况下，断面积预估模型推导结果如下:

根据蓄积收获模型式(25)，在已知林分未来断面积G2的情况下，收获预估模型推导结果如下:

2．6 模型检验结果与分析

2．6．1 生长模型检验

用独立样本对生长模型进行检验，对实际值与理论值进行一元线性回归求解实际值与理论值的相关系数r，查相关系数临界值表判断在α=0．01显著水平上实际值与理论值相关关系是否显著。各模型实际值与理论值相关系数以及预测精度如表2。

表2 各模型精度表Tab．2 The table of model precision

可以看到生长模型理论值与实际值之间的相关关系数均在0．8以上，查临界值表理论值与实际值相关关系均显著，且预测精度都在96%以上，预测精度很高。所以，模型精度精度符合要求，可以在生产实践中应用。

2．6．2 收获预估模型检验

收获预估模型是基于样地立地质量和初植密度这2个指标不随林分年龄改变而改变这一原则推导出来的，所以，对收获预估模型精度的检验需要固定样地复测数据。由于客观条件限制，尚未收集到这一部分数据，本文采取空间代替时间的方式，用地位指数和初植密度接近的不同年龄样地数据进行比较，检验过程如表3。

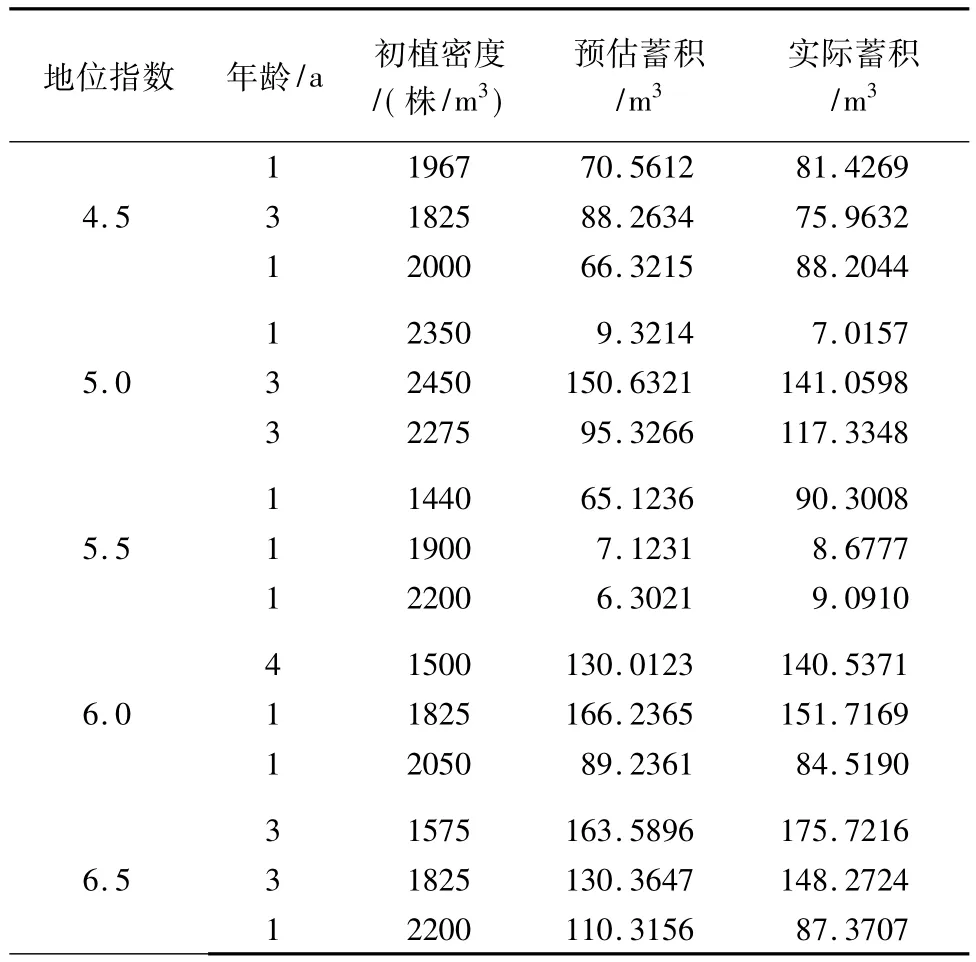
表3 收获预估模型精度检验Tab．3 Accuracy test of yield forecast models

计算预估蓄积和实际蓄积两组数据的相关系数，得到r=0．9620。当显著水平α=0．01、自由度(nm)=14时，查相关系数临界值表得:r0．01(14)= 0．6226。由于r＞r0．05(14)，所以在α=0．01显著水平上，预估蓄积与实际蓄积之间的相关关系显著，预估精度P%=97．25%。收获预估模型预测精度较高，可以在实际生产中应用。

3 结论与讨论

3．1 结论

1)根据Reineke方程定义，采用多次消去剔除立木度不足的方法模拟了林分近似完满立木度时lnN与ln Dg的关系。结果表明拟合效果较好，这种方法是可行的。对于林分密度指数模型的研究，主要参考前人的研究结果，根据林分年龄和林分密度指数的散点图将林分密度指数看成是随着年龄而变化的S型曲线，用Korf方程模拟其相关关系，将初植密度和地位指数引入方程构造模型。由于Korf方程和Richards方程的普适性，在今后的研究中可以进一步比较这两个方程拟合效果，选择最优方程。

2)构造断面积模型时，基于Bertalanffy同化－异化方程，将地位指数和林分密度指数引入方程的参数，在式(20)中，该方程有一个特解即(t，G)= (0，0)，可以理解为当林分年龄为0时，断面积为0。李希菲等最早提出了基于Bertalanffy同化－异化方程的Richards型断面积模型，但在将特解代入方程时采用的是(t，G)=(t0，0)，t0表示树高达到胸高(1．3m)时的年龄，所以推导出的Richards型断面积模型含有这一指标，后面学者在拟合断面积模型时多采用的是这一推导结果。从数学的严谨性方面考虑，本文认为(t，G)=(0，0)更为合理。

3)收获模型采用的是Schumacher可变密度的收获模型，剖析该模型可以发现当蓄积连年生长量达到最大时的年龄，即Schumacher模型拐点对应的年龄tZmax=β2/2，假如G与地位指数L和林分密度指数SDI不相关，则林分蓄积与L和SDI无关，显然与实际不符，所以断面积模型中引入L和SDI。这样做克服了Schumacher可变密度收获模型蓄积生长速率最大时的年龄tZmax与L和SDI无关的缺陷，使得模型基于现实情况下的可解释性更强。

4)收获模型是根据数学的四则运算变换得出的，根据模型系统可以预估一个轮伐期内的收获量。首先需要对预估对象进行标准地调查，计算现在的林分公顷断面积和公顷蓄积，再由断面积预估和蓄积预估模型预测未来的断面积和蓄积。其中林分现在的断面积和蓄积，不由断面积模型和蓄积模型计算得出而是直接由标准地调查的数据计算得出。由现实值推算未来值比理论值推算未来值更具有说服力。在收获模型精度检验时，采用了空间代替时间的方式对模型进行检验，但最好的办法是采用固定样地复测数据，这样检验的效果和精度更为准确。

5)本文利用190块临时标准地数据，构建了桉树人工林生长与收获预估模型系统。模型包括:地位指数模型、Reineke林分密度指数方程、林分密度指数模型、断面积生长模型、蓄积生长模型、林分密度指数预估模型、断面积预估模型、蓄积预估模型。生长与收获预估模型系统的建立能够为纸浆材桉树桉树人工林的可持续经营提供理论依据，为营林人员决策提供数据支持，同时也有利于促进桉树人工林的高效培育。

3．2 讨论

1)扩大样地的空间范围

样地位于雷州林业局北部的北坡林场和位于中部的石岭林场，由于台风因素导致南部临海的桉树人工林受灾严重，基本全部倒伏，未能在南部设置临时标准地。所以模型的数据来源并没有充分覆盖整个雷州林业局营林区域，代表性有所欠缺。

2)细分模型的年龄节点

通常在研究树木生长模型时，默认的年龄节点为1年。但对于速生树种来说，树木生长速度非常快，如果以1年作为节点则会出现较大误差。将年龄节点缩小(如3个月、4个月或半年)后模型是否更精确，这个问题有待进一步研究。

［1］曾伟生，骆期邦，贺东北，等．海南省主要树种相对树高曲线模型应用研究［J］．中南林业调查规划，1999(2):1－7．

［2］梁理勇．雷州刚果12号桉W5无性系林分蓄积量与胸径树高密度及其之间关系的探讨［J］．广东林业科技，2004(3):25－27．

［3］周元满，谢正生，刘新田．Richards函数在桉树无性系林分生长预测上的应用研究［J］．西南农业大学学报:自然科学版，2005 (2):240－243．

［4］李宗俊，刘萍，朱英娟，等．纸浆材桉树人工林地位指数表的编制［J］．林业资源管理，2016(1):59－64．

［5］Reineke L H．Perfecting a stand-density index for even-aged forests［J］．J．Agric．Res．1933，46(1):627－638．

［6］Bertalanffy V L．Quantitative laws in metabolism and growth［J］．Quarterly Review of Biology，1957，32(3):217－231．

［7］李希菲，唐守正，王松林．大岗山实验局杉木人工林可变密度收获表的编制［J］．林业科学研究，1988(4):382－389．

Study on Growth and Yield Forecast Model for Eucalyptus Pulpwood Plantation

LI Zongjun，MO yanqing，MO Xiaoyong，ZHAO Xueli，LIU Ping
(College of Forestry and Landscape Architecture，South China Agricultural University，Guangzhou 510642，China)

The eucalyptus pulpwood plantation of State-run Leizhou Forestry Bureau was taken as the research object and the eucalyptus pulpwood plantation growth and yield model was studied based on the data of 190 sample plots surveyed in January to February in 2015．SPSS 19.0 and ForStat 2.2 were used.Results show that density index model is SDI=1.7470N01.0951e－3.7637t0.05－0.1742L，basal area growth model is G = 16.7828L0.1529(1 － e－1.0125×10－8SDI－2.1970t)0.5554，volume model is M = e2.3641+0.0988L－3.0557t－1G0.9126．The research results can provide theoretical basis for forecast of growth and yield，determination of forest mature age and forest resources management for eucalyptus pulpwood plantation in State-run Leizhou Forestry Bureau.

Eucalyptus pulpwood，plantation，SDI，growth and yield forecast

S757.2

A

1002－6622(2017)01－0031－06

10．13466/j．cnki．lyzygl．2017．01．007

2017－01－20;

2017－02－03

桉树高效培育技术研究(2016YFD0600505);广东省林业科技创新专项(2013KJCX013－01，2015KJCX026);广东省省级科技计划项目(2014B020202013)

李宗俊(1990－)，男，安徽滁州人，在读硕士，从事林业调查规划设计。Email:forestzj0616106@126.com

刘萍(1964－)，女，陕西绥德人，博士，教授，从事专业森林经理、林业系统工程。Email:bengtiaoliu@126.com