不失一般性，追求简捷性

甘肃省会宁县第五中学 薛莲花

不失一般性，追求简捷性

甘肃省会宁县第五中学 薛莲花

追求简捷是数学解题永恒的主题，简捷美是数学美的基本特征, 简捷性原则是数学思维的优化，解题实践的优化，体现着数学的内在美。追求解题的简捷，是根据一般性寓于特殊性之中的原则进行的，在不失一般性的前提下，根据不同题型选择最佳方案，避繁就简，使问题迅速得到求解。在解题时对于简捷美的追求,不仅能激发钻研数学的兴趣,而且往往可以独辟蹊径,发现优美而简捷的妙解。

简捷性；问题特殊化；数形结合；巧妙代换

简捷性原则是数学思维的优化，解题实践的优化，体现着数学的内在美。追求解题的简捷，是根据一般性寓于特殊性之中的原则进行的，在不失一般性的前提下，根据不同题型选择最佳方案，避繁就简，使问题迅速得到求解。

一、应用概念，法则解题

数学概念通常是以定义、性质的形式表达的，而法则、结论又是概念推理的结晶。因此，利用定义、性质、法则和结论的钥匙，能沟通数学问题的内在联系，使解答简捷明快。

例1 已知过抛物线y2=2px(p＞0）的焦点F的直线l依次交抛物线及其准线于A,B,C三点，若，求抛物线的方程。

分析：分别过A,B两点作AD,BG垂直准线于点D，G。

∴抛物线方程为y2=3x。

二、问题特殊化

在某些情况下，特殊化方法能认识事物的本质，个性寓于共性之中。选择题和填空题的特征值法，就是基于这个原则。

例2 E、F分别是△ABC的边AB、AC的中点，△AEF和梯形EFCB绕BC旋转一周所得的几何体的体积分别是V1、V2，则V1，V2的大小关系是_________。

分析：如图1所示，设BE=DF=r，BC=h，

注：本题既是形的特殊化，又是量的特殊化，两者结合，独辟蹊径，干脆利落。

图1

三、数形结合

数与形紧密联系，相辅相成。华罗庚说：“数缺形时少直观，形少数时难入微。”有些数量借助于图形，可使抽象的概念和复杂的关系直观化、形象化、简单化。特别是那些不要求表示推理计算过程的选择题和填空题，更宜于运用图象直接答题。

分析：求出函数f(x)的表达式，画出f(x)的图象，数形结合求解。

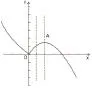
图2

四、仔细观察，先入为主

观察是解题的第一步，许多优美的解法正是来自于深刻、敏锐的观察。仔细审题，分清条件和结论，然后打破常规，迅速解答。

例4 已知正四面体的棱长为a，求此四面体对棱上两点的最短距离。

分析：异面直线上两点间距离公垂线段最短。易证正四面体对棱中点的连线就是其公垂线段。因此，所求的最短距离是。

注：求最（极）值一般先建立目标函数，再求函数的最（极）值，本题绕过了建立目标函数这一步，妙不可言。

五、整体思维，巧妙代换

中学数学是由代数、三角函数、立体几何、平面解析几何等有机结合的一个整体，各种量之间也有着内在的联系。因此，解题中从全局着眼，整体把握条件和结论，摆脱局部细节中一时难以弄清的数量关系的纠缠，常常会收到事半功倍之效。

例5 在球面上有P、A、B、C的四点，若PA、PB、PC两两垂直，且PA＝PB＝PC＝a，那么此球面的面积是多少？

分析：解本题时，大都先设法求出过A、B、C的圆半径，再根据球截面有关性质求球半径而得球表面积。若从局部到整体，以PA、PB、PC为棱构成球内接正方体，从整体出发考察，球的直径恰好是此正方体的对角线长，这样可立即求得球面积为3a2。

[1]王淼生.追求简捷是数学解题永恒的主题——从均值不等式在竞赛题中的应用谈起[J].中学数学月刊，2013（6）.

[2]齐红.数学的简捷美及其在解题中的应用[J].新课程：教育学术，2011（3）：109-110.