保拓扑结构的三维细化算法及三维非接触测量

洪汉玉+马尔威+黄丽坤

【摘要】 针对现有的三维细化算法会出现断裂、不连续以及破坏物体原有的拓扑结构等问题，提出了一种基于保拓扑结构和具有旋转不变性的新的三维细化算法。实验结果表明，新的细化算法具有连通性保持不变，几何及拓扑性质保持不变，及旋转后细化结果保持不变的性质。

【关键词】 三维细化 删除模板 拓扑结构 旋转不变性 三维非接触测量

一、引言

图像细化广泛应用在各个领域，如医学图像分析，模式识别等。三维图像细化是图像处理和视觉分析的主要研究方向，细化提取的骨架是后续图像分析和特征提取的重要基础。从三维细化的结果中可提取基本尺寸和基准线、基准面等特征，包括物体的轴线基准、轴线长度，形状结构及联接关系。通过这一系列参数和特征准确表述和确定目标的当前状态，从而实现对三维目标的全方位的非接触测量。

三维细化算法主要包括提取中心线和提取中心面两类，本文重点研究中心线的提取。在一个三维二值图像中黑点和白点分别代表目标点和背景点，细化就是将逐层将黑点移除（黑点改为白点）直到仅剩一个像素宽的骨架。连通性及拓扑结构的保持是三维细化过程中考虑的主要问题，概括为三个方面：（1）输入图像中的任何物体不能被拆分或完全消除；（2）任何空腔不能与背景或另一个空腔合并；（3）不能消除或新增任何的空腔和孔洞。连通性的保持是拓扑性质的保持的基础，例如形如“o” 的物体细化后不能形如 “c”，细化后提取的骨架应位于物体的中轴，并且看起来相似于原物体；同时细化算法在物体平移、比例变化及旋转前后提取的骨架应基本保持一致。

提取中心线的三维细化算法多是基于模板的并行细化算法。并行细化算法有子迭代并行细化算法，区域并行细化算法[10，11]和完全并行细化算法三类。完整的基于模板的完全并行三维细化算法由Ma和Sonka提出，这一算法不能很好的保护三维物体的拓扑结构，后续研究者发现这一问题，Wang和Basu通过扩充删除模板解决了某些情况下细化结果出现断裂的情况，但仍存在一些问题，且由于删除模板扩充后有方向性，不能保证三维物体旋转后的细化结果保持不变。

针对上述问题，提出一种新的细化算法，从基础模板在各个方向上旋转得到具有各向同性的删除模板，保证了模板的对称性，使物体旋转之后细化结果和旋转前细化结果保持一致；给出了真伪删除点的定义，并证明了提出的算法满足连续性保持的条件，解决了点同时删除造成不连续的问题。

二、三维细化旋转不变性理论分析

Wang和Basu针对Ma和Sonka的算法中不能保持连通性的情况对D类模板添加更多更细致的限制，扩充了最终的删除模板。Ma算法中D类删除模板是12个，Wang对模板中的一些点增加了限制，把D类模板扩充为36个。Ma算法中d7如图2所示，Wang扩充后的d7如图3所示。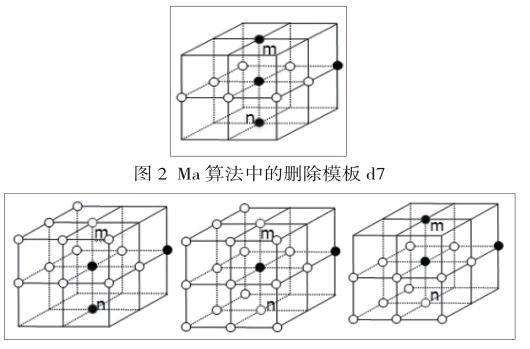

图3 Wang算法中删除模板d7-1，d7-2，d7-3算法主要步骤：

1）检测边界点（26邻域内至少有一个是背景点）。

2）并行删除满足任一删除模板的非尾点。

3）返回1）直到無任何点可以被删除。

完全并行细化算法，从各个方向同时逐层删除三维物体中的点，这保证了最终结果位于原物体的中轴上，且相似于原物体。但并行细化算法的细化结果有出现断裂的可能，每一层的点在进行删除模板的匹配及其他删除条件的判断时，若点与点之间相互为满足删除条件的必要点，同时删除所有满足条件的点得到的细化结果就可能出现断裂，不能保持原物体的拓扑结构。

其他情况下仍仍然会出现断裂，使最终细化结果无法保持原物体拓扑结构。同时因为只改变了某些方向上的模板，最终的删除模板不再是完全对称，使得细化算法不具旋转不变性。

三、基于保拓扑结构和旋转不变性的细化算法

针对上述分析提出一种新的基于保拓扑结构和旋转不变的三维细化算法。首先给出旋转不变性的定义，其次设计了各向同性的删除模板，最后根据需要定义了真伪删除点，并论述了提出的算法满足连续性保持的条件。通过假设验证法，检测候选删除点删除前后26邻域内目标体和背景组的数目变化，确认删除点的真伪，保持了原有的拓扑结构，进而确保物体旋转后细化结果的连续性不变。

关于旋转不变性做如下定义：

定义1（旋转不变性）：当物体相对之前位置旋转后，通过细化提取的骨架与旋转前提取的骨架形态及结构保持一致，简称该细化算法具有旋转不变性。

为使旋转后结果与旋转前结果保持一致，本文构造了具有各向同性的删除模板。如图4所示，新算法中具有各向同性的D类删除模板是12个，且模板中限制点比Ma算法中少。改进删除模板是基于图2中四类基本模板，通过绕三个中轴旋转获得，在结构上是完全对称的，从而保证在各个方向模板是同性的，使新算法具有旋转不变性。

为准确表达该算法，做如下定义：

定义2（真伪删 除点）：在每次迭代中，通过与删除模板的匹配，简单点、非尾点的判断选出候选点，假设所有候选点被删除，再逐个检验候选点被同时删除后26邻域内目标体的数目和背景组的数目有没有改变，若改变称为伪删除点，若未发生变化称为真删除点。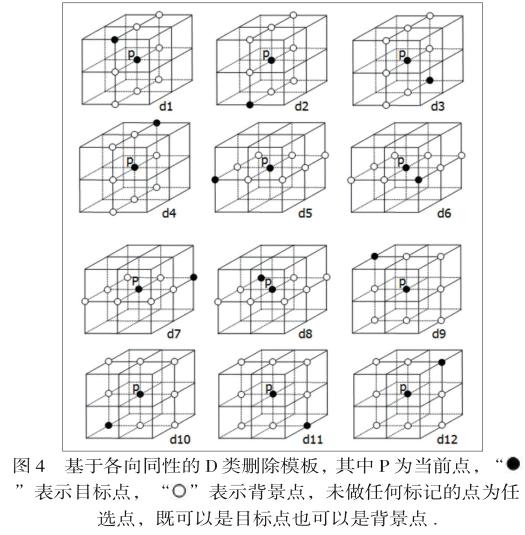

每次迭代中对符合删除模板且满足其他删除条件的目标点做标记，假设标记点已全部被删除（值为0），逐个对标记点位置进行检测，检测标记点位置26邻域中目标点（黑点）的连通性，和18邻域中背景点的连通性，若连通性发生改变则把标记点重置为1，若未改变确定删除。因为在一次迭代中任何点的删除不应该改变其26邻域中目标点的连通性和18邻域中背景点的连通性。这就有效防止同时删除一系列点造成细化结果出现断裂破坏拓扑结构的可能。

连通性证明：本文算法按照简单点的定义选候删除点，为保证被删除的点是简单点，在删除前做如下判断：判断当前点26邻域内的目标点是否连通；判断当前点18邻域内的背景点是否连通且至少有一个点与当前点是6邻接，所以被删除的点都是简单点，满足条件①。通过删除点的真伪验证表明对每一个删除点来说，在其他点被删除后，26邻域内仍然只有一个目标体，18邻域内只有一个背景组，即还是简单点，所以每次迭代中同时删除的所有点的集合是一个简单点集合。那么属于一个单位正方形上的两个，三个或四个不同点被同时删除时，它们也是简单点集合，表明本文算法满足条件②、③、④。假设存在一个包含在单位立方体内的目标体被完全删除，那么单位立方体内八个点只能是可被删除的点或者背景点，可被删除的点必须满足某一删除模板，根据根据本文算法设计的删除模板特点，八个点中总有一个面上的四个点必须同时是背景点，因此包含在一个单位立方体内能被完全删除的目标体不存在，即满足条件⑤。因此本文算法满足三维细化算法保持连通性的条件。

基于保拓扑结构具有旋转不变性的三维细化算法主要步骤：

1）检测边界点（26邻域内至少有一个是背景点）；

2）检测满足任一删除模板同时属于非尾点和简单点的点，并标记为候删除点；

3）根据定义2判断2）中标记的候删除点的真伪，若为真，则确认删除，否则不删除；

4）返回1）直到无任何点可以被删除。

四、 物体的尺寸提取与非接触测量

对细化后的骨架进行像素数的统计可以得到三维模型的几何尺寸信息，这些测量信息可以精准地描述三维模型的当前状态。比如表面即为边界点的集合，通过判断是否具备空间26连通可以快速提取边界点，表面积可以表示为边界点像素的总和，这种表示方法不仅简单，而且被证明是物体表面积的无偏和一致的最好估计。

根据三维图像数据和尺寸基准线，可提出和计算目标的厚度、高度、径向、轴向、位置等几何尺寸，计算各组成部分的长度、高度、宽度或直径、半径等形状参数，计算表面各部分的几何距离，有关结构与重要基准面、基准线的距离以及平行度、平面度、圆度、同轴度等形位误差。用这一系列参数和特征准确表达和确定目标的实际当前状态，从而实现对目标的全方位的非接触测量。

五、实验结果与分析

该部分设置了四个实验。在前两个实验中把新算法分别和Ma的算法，Wang的算法做对比，表明新算法在保持连通性方面的优势；在第三个试验中把新算法与Wang的算法的细化结果做对比，表明新算法具有旋转不变性；第四个实验是新算法细化各类模型得到的精準的骨架。

新算法与Ma算法的细化结果对比如图5所示，在图5.（a）中是一个连续的简单模型，图5.（b）中是Ma算法的细化结果，左右连在一起的两个方形在细化后被分开，破坏了原有的连通性，图5.（c）中是新算法的细化结果。左右两个方形细化后任连在一起，保持了原有的拓扑结构。在图6.（a）中是一个连续的简单模型，图6.（b）中是Ma算法的细化结果，上下连在一起的两个方形在细化后被分开，破坏了原有的连通性，图6.（c）中是新算法的细化结果。上下两个方形细化后任连在一起，保持了原有的拓扑结构

六、结论

完全并行基于模板的细化算法，会出现断裂，导致细化结果拓扑结构发生改变，并且不具有旋转不变性，本文通过设计各向同性模板，判断后删除点的真伪解决了这一问题，并通过实验进行了验证；在三维细化的基础上实现了非接触测量，提取三维特征信息，这将进一步满足对三维模型特征分析的需求。

参 考 文 献

[1]廖开阳，张学冬，章明珠.一种新的指纹图像快速细化算法[J].计算机工程与应用，2008，44（5）：93-95.

[2]邓刚，童学锋.FPTA快速细化算法在脱机手写体汉子识别中的应用.计算机工程与应用，2002，01：135-136

[3] Chuang JH， Tsai CH， Ko MC. Skeletonization of three-dimensional object using generalized potential field[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000，22（11）： 1241-1251.

[4]侯培，田庆国，葛宝臻.基于优化DRG的三维人体点云骨架提取算法[J].计算机工程与应用，2014，50（18）：182-187.