一种基于动态时间弯曲距离的快速子序列匹配算法
2017-04-10刘晓影
刘晓影


摘 要: 动态时间弯曲距离在用于计算时间序列间的距离时是极其耗费时间的,尤其是处理较大规模的时间序列数据库中的子序列匹配问题时,时间消耗更是难以忍受。该文提出一种新的低边界距离,能够快速滤掉不满足结果条件的时间序列,以提高查询速度,并证明该低边界距离不会丢弃真实的结果。一种基于水平边界区域的索引技术被用于进一步提高查询效率。分别以真实数据集和人造数据集作为实验数据来测试该文所提出的算法的性能,结果表明该算法在数据库规模上和序列长度上都有良好的健壮性。
关键词: 时间弯曲距离; 低边界距离; 范围查询; 数据库
中图分类号: TN911?34; TP311.13 文献标识码: A 文章编号: 1004?373X(2017)06?0025?06
Abstract: It is very time?consuming to calculate the distance between time sequences by using dynamic time warping distance, especially when the subsequence matching in large time?series databases is concerned. A new method of lower bound distance is presented in this paper, which can quickly filter the time sequences which are unable to satisfy the result condition, so as to improve the query speed. It is proven that the true results can not be lost if the method is used. To further increase the query speed, a technique for building an index based on skyline bounding region is also proposed. Some experiments with the data from real data set and synthetic data set were carried out to verify the performance of the methods. The results reveal that the method has robostness in the scale of database and sequence length.
Keywords: time warping distance; lower bounding distance; range query; database
0 引 言
时间序列是由一些在特定时间点上采样得到的实数组成。在现实世界中,有很多时间序列的例子,如股票的价格、天气的变化情况、商品的销售记录。时间序列间的相似性查询就是从时间序列数据库中发现与给定查询序列有相似的变化模式的序列,该操作在很多新的数据库应用领域(数据挖掘、数据仓库)中是很重要的,它能用于预测未来发展趋势、识别新的模式、发现规则[1?3]。例如,可能需要找出一天的股票价格中的特定模式来预测未来发展趋势;也可能需要找出历史上与今天有相似磁暴模式的日子来预测地球磁场的变化。
通常,时间序列相似性查询可以分为两类:全序列匹配和子序列匹配。全序列匹配是给定一条查询序列,在数据库中找出与其相似的完整数据序列,而子序列匹配是在数据库中找出与其相似的部分数据序列,即子序列。全序列匹配又可以看成是子序列匹配的一种特殊情况[3?5],故子序列匹配比全序列匹配有更广泛的应用。本文重点研究子序列匹配。
子序列匹配就是在给定一变长时间序列数据库、一长度为N的查询序列Q和阈值ε的情况下,从数据库中找出所有与查询序列相似的子序列(即子序列与Q之间的距离小于ε),并返回这些结果。
1 子序列匹配
在介紹子序列匹配前,先说明本文所用到的符号以及它们的定义,见表1。
1.1 动态时间弯曲距离
动态时间弯曲(Dynamic Time Warping,DTW)距离不要求时间序列中的元素与元素之间进行一一对应匹配,允许序列中的元素自我复制后再进行对齐匹配。当时间序列沿时间轴发生弯曲时,可以在弯曲部分进行自我复制,使两条时间序列之间的相似波形进行对齐匹配。DTW距离很好地解决了时间序列发生时间轴伸缩和弯曲后的相似性度量问题。例如,给定两条序列P=<4,5,6,8,9>和Q=<3,4, 7,8,9,7>,可以分别将这两条序列拉伸为P′=<4,5,6,6,8,9,9>和Q′=<3,3,4,7,8,9,7>,通过计算P′和Q′间的距离来衡量P和Q间的距离。在这种情况下,就称序列P和Q之间相互“调整”。P和Q之间“调整”的路径称为弯曲路径。在两条序列间存在多条弯曲路径,可称根据最小弯曲代价的路径计算的距离为动态时间弯曲距离。
表1 符号及其定义
由于存在多条弯曲路径,找到最小弯曲代价的路径是极其耗费时间的。为了解决这一问题文献[6]介绍了一种基于累积距离矩阵的动态规划方法来计算两条时间序列之间的DTW距离,时间复杂度为O(MN)。累积距离矩阵实际上是一个递推关系。给定两条时间序列P=
[DDTW(P,Q)=f(M,N)f(i,j)=d(pi,qj)+minf(i,j-1)f(i-1,j)f(i-1,j-1)f(0,0)=0, f(i,0)=f(0,j)=∞i=1,2,…,M; j=1,2,…,N] (1)
式中,d(pi,qj)表示序列元素pi和qj之间的距离,可以根据应用而选择不同的距离度量,比如d(pi,qj)=[pi-qj]。
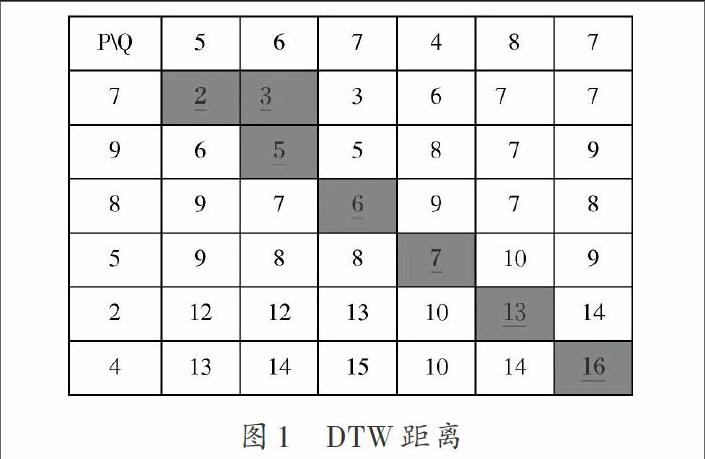
使用动态规划方法计算数据序列P和查询序列Q间距离的同时,通过累积距离矩阵也可获得所有P的前缀P[-,e]与Q之间的距离。例如,给定数据序列P=<7,9,8,5,2,4>和查询序列Q=<5,6,7,4,8,7>,以及查询阈值ε为8。在计算P和Q间的距离时,也可得到所有P的前缀中与Q的距离小于8的子序列。图1给出了P和Q间的累积距离矩阵。图1中阴影部分表示两条时间序列之间的具有最小代价的动态时间弯曲路径,累积距离矩阵的右下角得到的值就是这两条时间序列之间的距离16。通过累积距离矩阵中的最后一列可以获得P的前缀与Q之间的距离,即DDTW(P[-,1],Q)=7;DDTW(P[-,2],Q)=9;DDTW(P[-,3],Q)=8;DDTW(P[-,4],Q)=9;DDTW(P[-,5],Q)=14;DDTW(P[-,6],Q)=16。因此,P[-,1]和P[-,3]就是子序列匹配的结果。
子序列匹配时,可以通过检测数据序列的所有后缀与查询序列的距离来获得完整的匹配结果。进行子序列匹配的时间复杂度为O(M2N)。
1.2 相关工作
目前已有很多研究工作是研究如何索引时间序列才能在DTW距离下做高性能的查询[5,7?9]。
文献[8]中,作者设计了一种DTW距离的低边界函数Dtw?lb,该距离满足三角不等式。一个四元的特征向量用于Dtw?lb的计算,该特征向量是提取序列的第一个元素、最后一个元素、以及序列的最大值、最小值。为了提高查询速度,可用高维索引来存储这些四元特征向量,用Dtw?lb作为距离函数。然而,在文献中的结果表明这种近似是粗糙的,需要花费很高的搜索代价,进行大量的准确计算。
文献[7]提出了一种基于动态规划中的全局约束的查询方法。该方法根据弯曲路径的范围得到查询序列的“封套”(envelope),并计算出“封套”的PAA(Piecewise Aggregate Approximation)。查询序列与数据序列间的低边界距离被定义为“封套”的PAA与包含数据序列的最小边界矩形MBR(Minimum Bounding Rectangle)间的欧氏距离。这种方法当弯曲路径在狭小范围内时是有效的,但当弯曲路径范围变宽时查询性能将下降。
文献[9]中,提出了FTW(Fast search method for dynamic Time Warping)算法。算法使用一种低边界函数LBS(lower bounding functions)来近似计算DTW距离;使用Early Stopping算法来排除那些不能产生结果的弯曲路径;并采用Refinement算法来逐渐提高近似计算的准确程度。FTW用很低的计算代价就可排除大量的非结果序列,提高了查询效率。
由于任意两序列间的DTW距离与等长的序列前缀间不存在任何关系,故DTW距离下的子序列匹配变得更加复杂。文献[10]中,提出了一个利用动态规划求解两条时间序列DTW中心的方法,即以最小化中心序列到两条样本序列的DTW距离平方和为目标,递归求解最优解。文献[11]提出了一种基于前缀的查询技术,用文献[8]中提出的边界函数来进行子序列查询,然而,在文献[7]中指出“该低边界函数是松散的,大量非结果序列将不能被过滤掉”。
文献[12]扩展了文献[7]中的全序列匹配算法,该方法主要是基于滑动窗口和弯曲路径约束的,对于狭小范围下的弯曲路径匹配,该查询是很有效的,但当弯曲路径的范围变宽时,也将面临文献[7]中的问题,即查询性下降。
1.3 FTW技术
全序列匹配是子序列匹配的一种特殊情况,故可以通过扩展一些全序列匹配方法来进行子序列匹配。在1.2节中提到的FTW算法是一种全序列匹配的方法,它主要是基于三个思想建立的[9]:LBS距离、Early Stop Ping算法和Refinement算法。
LBS距离用于计算时间序列的近似序列间的距离,可评估时间序列间的DTW距离,但LBS距离的计算量要比DTW距离小很多。近似序列就是用较少的信息来表示时间序列的。近似序列由近似段组成,给定一条长度为M的时间序列P=
[pAi={pRi,pTi}, pRi={pLi,pUi}pLi=min{px,…,py}, pUi=max{px,…,py}x=1, i=1j=1i-1pTj+1, 2≤i≤n, y=j=1ipTj] (2)
式中:[pRi]和[pTi]分别是在该段中时间点上的数值范围和该段所跨的时间数;[pUi]和[pLi]分别代表[pRi]的上下边界。[pUi]和[pLi]分别是在从px到py的[pRi]个元素中的最大和最小的值。因此,P能近似地表示成PA=
定理1 设PA和QA分别是P和Q的近似序列,将有[DLBS(PA,QA)≤DDTW(P,Q)],其中[DLBS(PA,QA)]是近似序列间的距离。
EarlyStopping算法用于進行k?近邻查询。在得到最后k个结果之前会维护一个候选结果列表。当前第k个近邻与查询序列间的准确距离dcb可以用来过滤那些不能产生查询结果的弯曲路径。如果一个序列与查询序列间的距离小于dcb,就认为发现了一条相似序列,此时候选结果列表也将要更新,将会得到更小的dcb。Early Stopping算法通过使用dcb能够过滤掉那些不能产生结果的弯曲路径。即使是没有约束弯曲路径的范围(即全局约束没有被使用),该算法也能通过判断弯曲路径是否大于dcb来动态的缩减弯曲路径的范围。也就是说,dcb是减少弯曲路径范围的阈值。
Refinement算法使用不同粒度下的近似序列来评估DTW距离。这样做的好处是能够使DTW距离评估准确程度有一个逐渐增加的过程,当数据序列与查询序列距离很大时,通过在较粗糙的粒度下进行很少的计算来就可以判断出该数据序列不是结果序列。
2 低边界距离
子序列匹配得到的相似子序列的长度以及在数据序列中的开始位置是不定的,见图2。给定数据序列P=
3 基于水平区域边界技术的索引
子序列匹配过程中如果对数据序列进行索引可进一步提高查询性能。在FTW方法中,由于处理的是全序列匹配,即使没有对数据序列建立索引,也能取得很好的效果。但对于子序列匹配,所涉及的计算量将大大增加,故下面将介绍一种基于水平边界技术用于索引时间序列的方法。首先获得数据库中所有数据序列在一给定粗糙粒度下的近似序列,抽出这些近似序列的所有后缀来构造多维索引。索引的方法采用在水平索引[13]中所用到的水平边界区域SBR(Skyline Bounding Region)技术,即用一个被上下水平线和两条垂直线所包围的二维区域来表示序列所在的范围。如图3所示,图3中曲线为一近似序列的片斷,水平的实线用来表示近似序列在某一时间段内数值的变化范围,垂直的虚线表示时间段。根据近似序列的后缀得到的SBR可用于构建索引。上水平线TS(Top Skyline)和下水平线BS(Bottom Skyline)分别定义如下:
索引中,内部节点用于记录SBR以及指向SBR中所包含的后缀的叶子节点的指针,叶子节点中存放着近似序列的后缀。子序列匹配时,先计算查询序列Q的近似序列QA,然后再计算QA与每个SBR之间的距离。如果距离大于阈值ε,表明该SBR中不包含与查询序列相似的子序列,将被过滤掉;否则继续计算QA与该SBR中所包含的所有后缀P[s,-]A之间的距离。对于那些能产生结果的后缀,将通过计算原始数据序列P[s,-]与Q之间的距离来决定哪条子序列属于结果集。如果子序列P[s,e]与Q之间的距离小于阈值ε,该子序列将被加入结果集,同时记录该子序列在数据序列P中的起始位置以及子序列的长度,具体算法如下:
Algorithm SubSBRSearch(Q, ε)
Compute QA;
// range query
for each SBR do
dcoarse := EarlyStopping(SBR, QA, ε);
if all d in dcoarse is not above ε then
add SBR to TempList;
endif
endfor
for each SBR in TempList do
for each suffix PA[i, -] in SBR do
dapprox := EarlyStopping(PA[i, -], QA, ε);
if all d in dapprox is not above ε then
dexact := EarlyStopping(P[i, j], Q, ε);
if each d in dexact is below ε then
add P[i, j] to ResultSet;
endif
endif
endfor
endfor
return ResultSet;
4 实 验
4.1 实验数据
实验所用的数据集包括人造数据和真实数据。人造数据序列P=
[pi=pi-1+zi]
式中,zi是一个取值在[-0.1, 0.1]区间的独立同分布的随机变量。序列中第一个元素p1的值在[1,10]区间中随机选取。真实数据集来源于股票数据USA S&P 500(http://biz.swcp.com/stocks),数据集中包含545条序列,平均长度为231。查询序列的选取采用了与文献[11]相同的方法生成了100条查询序列,生成方法如下:
(1) 从数据集中随机选取一条数据序列;
(2) 从选取的数据序列中随机的抽取一段子序列;
(3) 在[[-std10,std10]]中为子序列中的每个元素选取一个随机值,std是序列的标准方差;
(4) 分别加随机值到子序列的相应元素中。100次查询的平均时间被用来做性能评价。
为了评估提出算法的性能,将在实验中比较以下三个算法:
(1) 本文提出的算法,记为SubSBR算法,在子序列匹配时,仅使用了一种粒度下的近似序列,近似段的每段有4个元素,t=4,用SBR建索引时每页大小为256 B;
(2) 改进原有FTW算法用于子序列匹配,记为SubRFM算法,在子序列匹配时,数据序列有三种不同的粒度,分别是t1=2,t2=8,t3=32;
(3) 顺序匹配算法,记为Sequential Search,在匹配的过程中没有建立索引,按顺序扫描数据库查找相似子序列。表2列出了实验中所用到的详细参数。
实验的硬件环境是:Pentinum 4 2.6 GHz的CPU、主存为512 MB;软件环境是:操作系统为Microsoft Windows xp,算法采用C编写。
4.2 性能比较
图4显示了建立SBR索引时页面的大小对查询时间的影响。页面大小的变化范围为64~1 024。从图4可以看出建索引时页面大小的增加对查询时间的影响不大。在不同页面大小下的所需的查询时间的标准方差仅为0.04。当页面大小为256时,所需的查询时间最少。图5显示了阈值ε与查询时间的关系。当阈值ε从30增加到170, SubSBR算法所需的查询时间要比顺序查询和SubRFM算法小很多。图6显示了查询序列长度与查询时间的关系。当查询序列的长度从70增加到130时,SubRFM和SubSBR无论是在查询时间还是在查询时间增长幅度上都要比顺序查询小很多。SubRFM和SubSBR这两个算法在查询序列長度的变化时,所需的查询时间相对稳定。
图7显示了时间序列长度与查询时间的关系。数据序列长度的变化范围是200~800,相应的查询序列的长度变化范围为70~280。随着数据序列的变长,数据序列中所包含的子序列的数量也会增加,这将导致查询时需要更长的时间。从图7中可以很明显地看到这一点。SubRFM和SubSBR这两种方法都优于顺序的查询方法,而且随着序列长度的增加,查询时间的增长幅度也比顺序查询小。SubRFM和SubSBR这两种算法分别比顺序查询快10.57倍和68.27倍;SubSBR算法平均比SubRFM算法快6.54倍。
图8显示了数据集大小对查询时间的影响。数据集中包含的序列从1 000变化到4 000时,三个算法所需的查询时间均有所增长。但SubRFM和SubSBR这两种算法增长幅度的比顺序查询缓慢,其中SubSBR算法所需查询时间最短,SubRFM和SubSBR这两种算法分别比顺序查询快6.12倍和43.18倍。SubSBR算法平均比SubRFM算法快7.05倍。
5 结 论
本文提出一种基于DTW距离的子序列匹配算法。该算法的优点有:查询速度快、可查询任意长度的子序列、不需要约束弯曲路径的范围和保证不产生假丢弃。本文的主要贡献有两点:修改了用于全序列匹配的LBS距离,使其能够处理子序列匹配,并证明该距离不会产生假丢弃;设计一种基于SBR的索引,并提出了相应的查询算法。实验显示本文所提出的算法在当序列的长度、数据集的大小以及阈值变化时也具有很好的性能。当数据序列长度变化时,提出的算法SubSBR平均比顺序查询快68.27倍;比SubRFM快6.54倍。当查询序列长度变化时,提出的算法SubSBR平均比顺序查询快32.37倍;比SubRFM快1.05倍。当数据集大小变化时,提出的算法SubSBR平均比顺序查询快43.18倍;比SubRFM快7.05倍。SubSBR算法是有很好的健壮性的,可用于大规模数据库中的子序列查询。
参考文献
[1] AGRAWAL R, FALOUTSOS C, SWAMI A. Efficient similarity search in sequence databases [C]// International Conference on Foundations of Data Orgazanation. [S.l.: s.n.], 1993: 69?84.
[2] 冯钧,陈焕霖,唐志贤,等.一种基于DTW的新型股市时间序列相似性度量方法[J].数据采集与处理,2015(1):99?105.
[3] FALOUTSOS C, RANGAUATHAN M, MANOLOPOULOS Y. Fast subsequence matching in time?series databases[J]. ACM sigmod record, 1994, 23(2): 419?429.
[4] CHU K W, WONG M H. Fast time?series searching with scaling and shifting [C]// Eighteenth ACM Sigact?sigmod?sigart Symposium on Principles of Database Systems. [S.l.]: ACM, 1999: 237?248.
[5] YI B K, JAGADISH H, FALOUTSOS V C. Efficient retrieval of similar time sequences under time warping [C]// International Conference on Data Engineering. [S.l.]: ICDE, 1998: 201?208.
[6] BERNDT J, CLIFFORD D. Using dynamic time warping to find patterns in time series [C]// AAAI Workshop on Knowledge Discovery in Database. USA: AAAI, 1994: 229?248.
[7] KEOGH E J. Exact indexing of dynamic time warping [J]. Knowledge and information systems, 2005, 7(3): 358?386.
[8] KIM S W, PARK S, CHU W W. Approach for similarity search supporting warping in large sequence databases [C]// International Conference on Data Engineering. [S.l.:s.n.], 2001: 607?614.
[9] SAKURAI Y, YOSHIKAWA M, FALOUTSOS C. FTW: Fast similarity search under the time warping distance [C] //Symposium on Principles of Database Systems. [S.l.]: ACM, 2005: 326?337.
[10] 孙焘,夏斐,刘洪波.基于动态规划求解时间序列DTW中心[J].计算机科学,2015(12):278?282.
[11] PARK S, KIM S W, CHO J S, et al. Prefixquerying: an approach for effective subsequence matching under time warping in sequence databases[C]// Acm Cikm International Conference on Informatio. [S.l.]: ACM, 2001: 255?262.
[12] Wong T S F, Wong M H. Efficient subsequence matching for sequences databases under time warping [C]// Proceedings of Database Engineering and Applications Symposium. [S.l.]: IEEE Computer Society, 2003: 139?148.
[13] LI Quanzhong, LOPEZ Lopez, MOON Bongki. Skyline index for time series data [J]. IEEE transactions on knowledge and data engineering, 2004, 16(6): 669?684.
[14] 赵慧,候建荣,施伯乐.一种基于分形时变维数的非平稳时间序列相似性匹配方法[J].计算机学报,2005,28(2):227?231.
