基于组合权重的灰色关联投影法的立交方案综合评价
2017-04-08马瑶
马瑶
(西安市政设计研究院有限公司,陕西 西安 710068)
科技研究
基于组合权重的灰色关联投影法的立交方案综合评价
马瑶
(西安市政设计研究院有限公司,陕西 西安 710068)
针对立交方案综合评价具有多目标的特点,建立了综合评价指标体系,提出了组合权重的灰色关联投影法。通过层次分析法与熵权法结合,确定评价指标权重,并应用灰色关联投影法对立交方案进行评价。结合工程实例对其进行验证,表明指标权重更科学合理,说服力强,结论更符合实际。
立交方案;组合权重;灰色关联投影;综合评价
0 引言
立交方案综合评价是一个复杂而难以彻底解决的问题,是一个既包含定性指标又包含定量指标的多目标综合评价问题,是一个灰色多目标评价问题。目前综合评价常用的方法有价值分析法[1]、层次分析法[2]、主成分分析法[3,4]、模糊综合评价法[5]及基于投影寻踪(Projection Pursuit)的综合评价法[6]等方法。本文结合立交方案特点,提出组合权重的灰色关联投影法。
1 建立综合评价指标体系
综合评价指标体系中第一层为目标层,用于不同方案间的比选;第二层为准则层,作为方案比选的基本原则;第三层为指标层,是各指标属性的具体描述;第四层为子指标层,是对功能指标中各指标属性的进一步细化。以西安空港新城某立交为例,依据实际情况及指标体系选取原则,选取以下因素作为综合评价指标(见表1)。
2 指标权重确定
2.1 层次分析法确定权重
根据建立的递阶多层次结构,依据表2,按其重要程度构造下层各因素对上一层准则的两两比较判断矩阵。设有m个评价指标,则判断矩阵I=(aij)mxm。

表1 综合评价指标表

表2 判断尺度定义表
判断矩阵只是针对上一层而言,经两两比较的评判结果,还要按需要将本层所有元素以上一层元素为依据排出优劣顺序。计算步骤如下:
(1)计算判断矩阵的每一列乘积Mi:
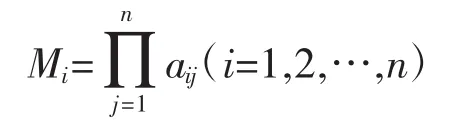
(2)计算Mi的n次方根
(3)对向量w=[w1w2… wn]T规范化
对各个判断矩阵的一致性进行检验。判断矩阵难免受到人为因素的影响,为衡量判断矩阵质量的优劣,对各个判断矩阵的一致性进行检验。
计算一致性指标CI和平均随机一致性指标CR:
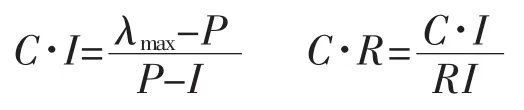
CI越大,说明判断矩阵一致性越差;CI=0时,表示具有完全一致性。当CR<0.1时即满足要求具有满意的一致性,否则必须重新调整判断矩阵[7]。
2.2 熵权法
设有m个评价指标x1,x2,…,xm,且有n个立交方案,即评价指标为xij(i=1,2,…,n;j=1,2,…,m),则第j个评价指标的熵定义为:

指标的熵越小,其熵权越大,表明各方案在该指标上有明显的差异,应重点考察。
2.3 组合权重的确定
从主客观赋权两个角度出发,确定组合权重。设由层次分析法确定的权重向量为W=[w1,w2,…,wm],由熵权法确定的权重向量为U=[1,2,…,m],令а、β分别表示这两种定权方法的相对重要程度,则组合权重V=[v1,v2,…,vm]可表示为:
vi=αwi+βi(其中0≤α≤1,0≤β≤1,α+β=1)
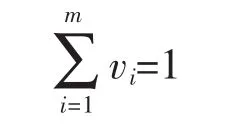
本文对两种方法确定的权重同时考虑,且认为重要性相同,一般取а=β=0.5。
3 组合权重——灰色关联投影法
灰色关联投影法是一种多因素统计分析方法[8-10],其核心是以各因素数据为依据计算投影值。
记立交方案的集合:
A={方案1,方案2,…,方案n}={A1,A2,…,An}
记Z是综合指标的集合:
Z={指标1,指标2,…,指标m}={Z1,Z2,…,Zm}
方案Ai对指标Zj的指标值记为Yij(i=1,2,…,n;j=1,2,…,m),对于纯定性分析的指标,只能依靠专家打分定级,取值如表3所示。对于定量指标,要将其化为无量纲的仅能反映方案优劣的指标值。
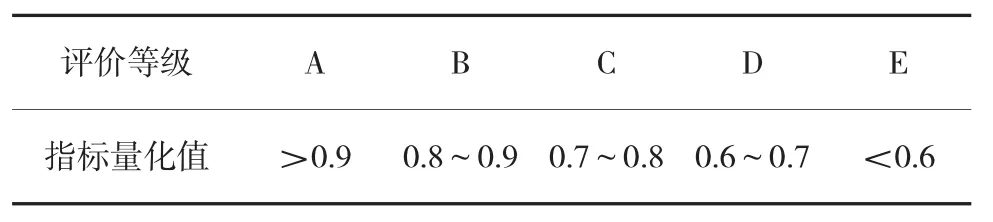
表3 评价等级量化表
计算比较空间Z中各方案点与理想方案点的关联度rij[9],有:

在加权向量V的作用下构造而成的增广型矩阵为加权灰色关联决策矩阵,且满足F':

将每个决策方案看成一个行向量(见图1),则每个决策方案Ai与理想方案A*之间的夹角余弦为:


图1 灰色关联投影法示意图
评价方案Ai在理想方案A*上的投影为灰色关联投影值Di:

根据这些投影值的大小,对多指标的比选方案做出科学的排序比较和分析。
4 实例分析
空港新城某立交综合评价指标根据文献[11]取值,如表4所示,其中定性指标值通过专家打分法得到。
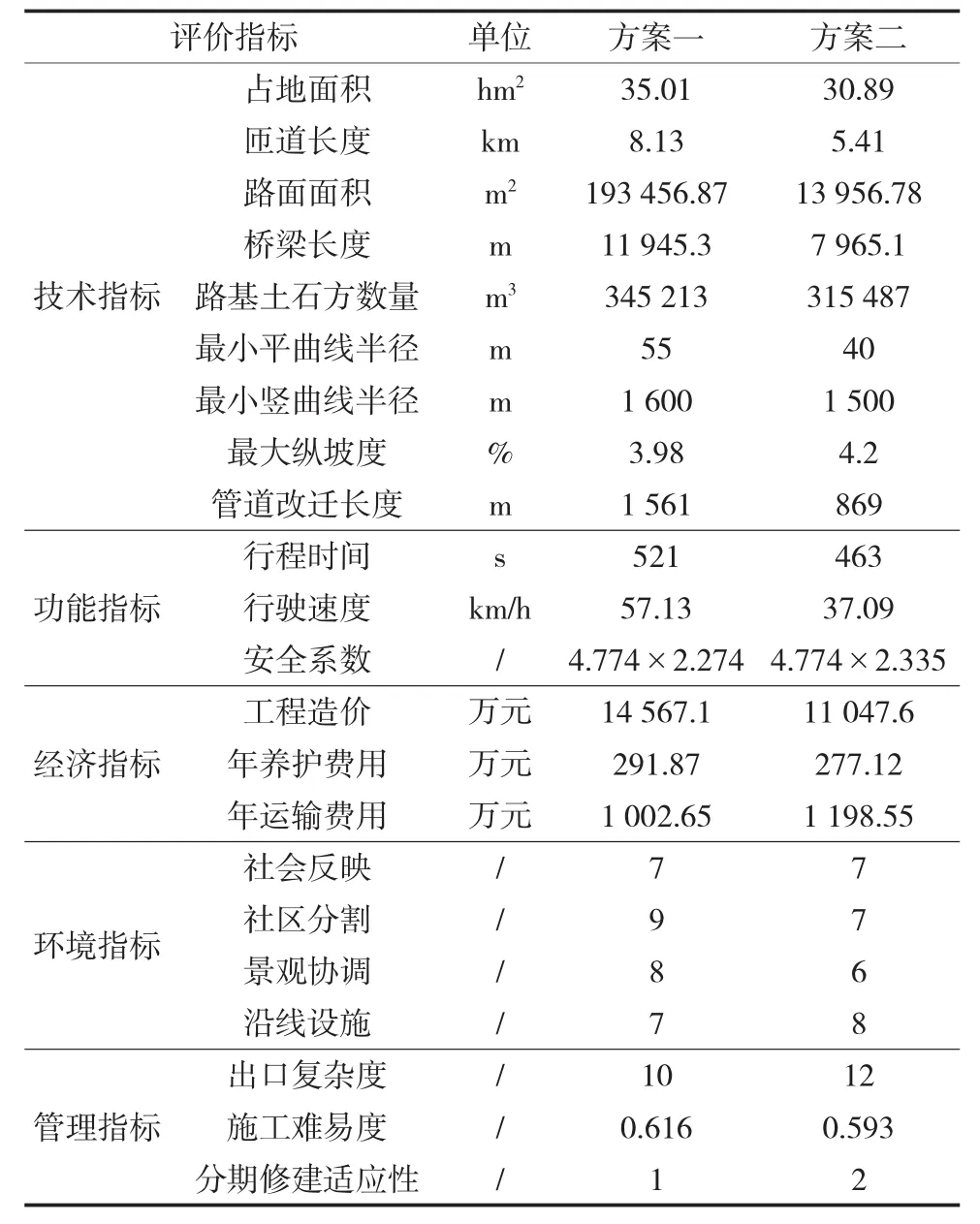
表4 空港新城某立交方案指标汇总表
依据层次分析法可计算得各目标权重,如表5所示。

0 . 3 2 5 6 4 2 0 . 2 2 6 5 4 3 0 . 3 2 6 8 9 2 0 . 0 7 8 9 5 4 0 . 0 4 1 9 6 9 c10 . 2 5 2 4 5 2 0 0 0 0 0 . 0 8 2 2 0 9 c20 . 1 9 5 4 6 7 0 0 0 0 0 . 0 6 3 6 5 2 c30 . 0 5 5 4 5 4 0 0 0 0 0 . 0 1 8 0 5 8 c40 . 0 5 1 4 5 3 0 0 0 0 0 . 0 1 6 7 5 5 c50 . 0 5 1 2 4 6 0 0 0 0 0 . 0 1 6 6 8 8 c60 . 1 4 4 2 3 5 0 0 0 0 0 . 0 4 6 9 6 9 c70 . 0 9 9 9 7 8 0 0 0 0 0 . 0 3 2 5 5 7 c80 . 0 9 7 8 9 1 0 0 0 0 0 . 0 3 1 8 7 7 c90 . 0 5 1 8 2 4 0 0 0 0 0 . 0 1 6 8 7 6 c10 0 0 . 4 2 8 4 0 7 0 0 0 0 . 0 9 7 0 5 3 c11 0 0 . 4 2 7 8 9 6 0 0 0 0 . 0 9 6 9 3 7 c12 0 0 . 1 4 3 6 9 7 0 0 0 0 . 0 3 2 5 5 4 c13 0 0 0 . 6 8 6 9 5 3 0 0 0 . 2 2 4 5 5 9 c14 0 0 0 . 1 1 4 5 9 6 0 0 0 . 0 3 7 4 6 1 c15 0 0 0 . 1 9 8 4 5 1 0 0 0 . 0 6 4 8 7 2 c16 0 0 0 0 . 0 9 6 5 5 2 0 0 . 0 0 7 6 2 3 c17 0 0 0 0 . 2 8 4 5 9 6 0 0 . 0 2 2 4 7 0 c18 0 0 0 0 . 5 1 9 8 7 6 0 0 . 0 4 1 0 4 6 c19 0 0 0 0 . 0 9 8 9 7 6 0 0 . 0 0 7 8 1 5 c20 0 0 0 0 0 . 4 6 6 3 8 5 0 . 0 1 9 5 7 4 c21 0 0 0 0 0 . 4 3 2 5 6 9 0 . 0 1 8 1 5 4 c22 0 0 0 0 0 . 1 0 1 0 4 6 0 . 0 0 4 2 4 1∑1 b1 b2 b3 b4 b5 ωi(i = 1,…,2 2)
依据熵权法计算结果见表6。
组合权重V=[v1,v2,…,vm]可表示为:vi=0.5Wi+ 0.5ui。其计算结果见表7。
计算得方案的灰色关联投影值D1、D2:
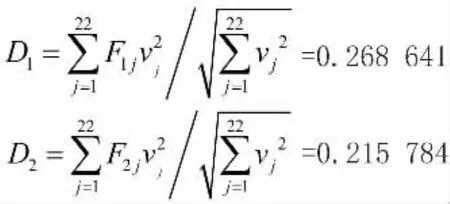
投影值越大可知方案越优,故推荐采用方案一。此案例计算结合了两种指标权重,更具有说服力。
5 结 论
组合权重的灰色关联投影法是在传统的灰色关联法中将指标进行更为科学合理的权重分配,用以对实际工程案例进行全面综合评价。在评价指标时,可根据实际情况对层次分析法及熵权法分别确定的指标权重进行二次调节。使用该方法,可以规避单纯权重确定方法引起的偏差,可以反应整体指标情况。对于立交方案评价及其他领域均具有借鉴意义。
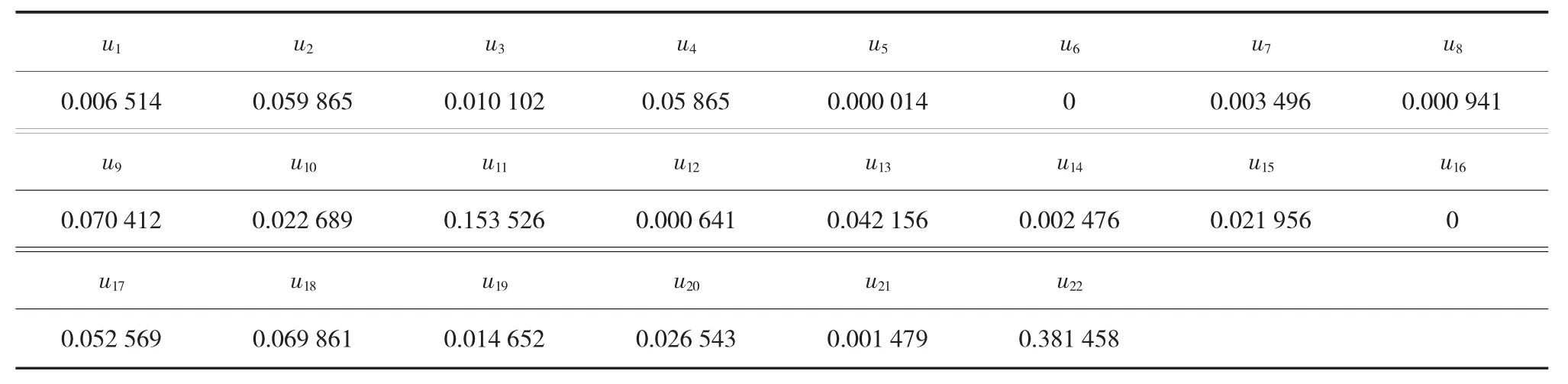
表6 评判指标熵权计算值表
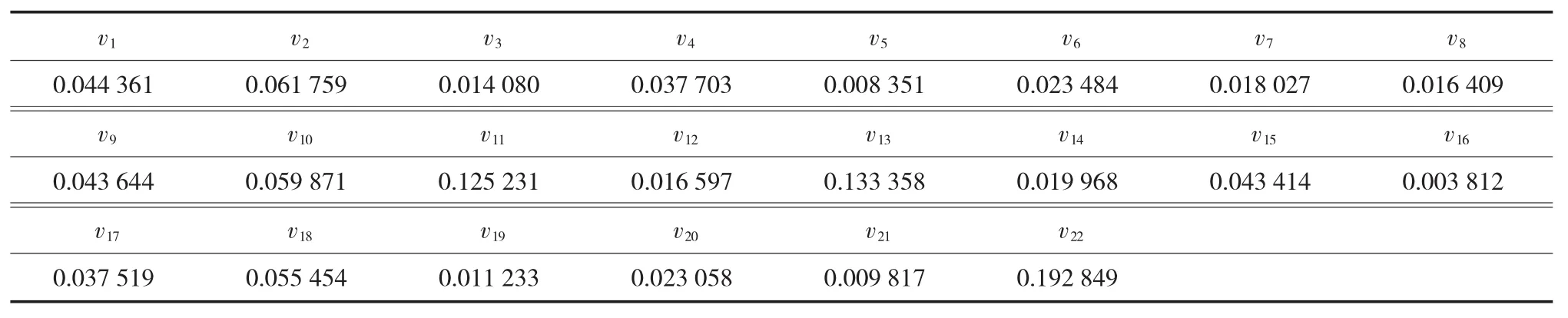
表7 评判指标组合权重计算值表
[1]王炜,邓卫,杨琪.公路网络规划建设与管理方法[M].北京:科学出版社,2001.
[2]Saaty T L.The Analytic Hierarchy Process[M].New York: McGraw-Hill,1980.
[3]任若恩,王惠文.多元统计数据分析—理论、方法、实例[M].北京:国防工业出版社,1997.
[4]何晓群.多元统计分析[M].北京:中国人民大学出版社,2004.
[5]杨少伟.道路立体交叉规划与设计 [M].北京:人民交通出版社,2000.
[6]李祚泳.投影寻踪技术及其应用进展 [J].自然杂志,1997,19 (4):224-227.
[7]周宪华.公路网规划与设计[M].北京:人民交通出版社,1991.
[8]魏权龄.评价相对有效性的DEA方法 [M].北京:中国人民大学出版社,1998.
[9]邓聚龙.灰色系统理论教程 [M].武汉:华中理工大学出版社, 1990.
[10]魏世孝,周献中.多属性决策理论方法及其在C3I系统中的应用[M].北京:国防工业出版社,1998.
[11]西安市政设计研究院有限公司.西咸新城空港新城沣泾大道立交方案设计[Z].西安:西安市政设计研究院有限公司,2013.
U412.35+2
A
1009-7716(2017)03-0192-04
10.16799/j.cnki.csdqyfh.2017.03.053
2017-01-10
马瑶(1983-),女,陕西绥德人,工程师,从事市政道路设计工作。
