基于能量法的成桥阶段高墩计算长度系数分析

元德壬，钟 明

（1.广西河百高速公路有限公司,广西 南宁 530021;2.西安中交土木科技有限公司,陕西 西安 710075）

基于能量法的成桥阶段高墩计算长度系数分析

元德壬1，钟 明2

（1.广西河百高速公路有限公司,广西 南宁 530021;2.西安中交土木科技有限公司,陕西 西安 710075）

高墩在成桥阶段墩顶边界条件介于铰接和固结之间，其计算长度系数往往难以取定。现通过构造成桥阶段高墩的形函数，利用能量法求解刚性地基高桥墩成桥阶段的失稳力临界力，又通过欧拉公式求得其计算长度系数，并结合算例采用有限方法和能量法进行计算，对比分析两者计算结果。结果表明：在计算高墩计算长度时，需计入墩顶非理想边界的影响。此外，所推能量法公式计算结果同有限元程序接近，具有较高精度，可供设计参考使用。

成桥阶段；高墩；计算长度系数；能量法

0 引言

由构件偏心受压构件承载能力计算公式可知，计算长度系数k是影响结构承载力的重要因素。但它仅给出了理想边界条件下的构件计算长度。事实上，工程中边界条件是非理想的。尤其是在确定成桥阶段下的高桥墩计算长度时，墩顶边界条件介于铰接与固结之间，这给设计计算带来了困难。

目前，计算高墩计算长度系数k的主要方法是通过对高墩进行稳定分析求解稳定临界力，然后利用欧拉公式反算得到k值。如何通过高墩稳定分析求解稳定临界力，白青侠[1]和赵明华[2]、[3]分析了高墩在施工阶段稳定性并给出了临界失稳力；郭梅[4]和刘进[5][6]基于弹性欧拉理论探讨了高墩大跨度连续刚构桥稳定性，分析了桥墩截面形式对稳定性的影响；程翔云[7]、[8]研究了支座刚度对高墩顶部约束刚度的影响，给出了墩顶抗推刚度的计算方法。目前，高墩稳定性研究限于墩顶自由和墩顶固结两种极端状况。对于一般高墩在成桥阶段时其边界约束受到支座和上部结构影响，墩顶水平位移与转角受到约束，其刚度并非无限大，介于固结和铰接之间。设计人员在选取成桥阶段下的高墩计算长度系数时往往采用经验值。因此，如何计算非理想边界条件下高墩计算长度系数具有实际意义。

本文通过构造成桥阶段高墩的形函数，利用能量法求解刚性地基高桥墩成桥阶段的失稳力临界力，并求得其计算长度系数，且结合算例采用有限方法和能量法进行计算，对比分析了两者计算结果。

1 结构势能泛函

选取成桥阶段高墩力学模型如图1所示。设墩高等截面为l，墩顶作用一竖向力P，墩身容重为g。为了便于研究墩顶弹性约束条件下的计算长度，在计算图式中，假定基础为刚性地基，墩底嵌固于承台上，这样可使形函数的构造得到简化。此外，墩顶用平动弹簧、转动弹簧模拟支座和主梁对墩的约束，不考虑竖向变位对墩的影响。于是结构的总势能的泛函为：

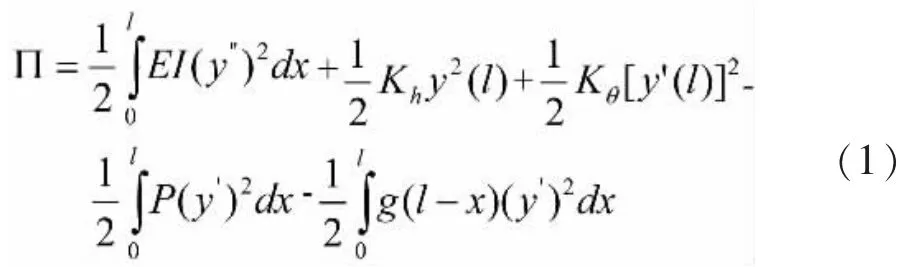
式中：Kθ为墩顶转动弹簧刚度；Kh为墩顶平动弹簧刚度；y(x)为高墩的形函数。

2 形函数的构造

目前，关于图1力学模型的形函数未有研究，给能量法表示桥墩的形变能造成困难，故需要对其形函数进行分析。考虑到图1力学模型中墩的变形介于以下两种变形之间：其一为墩顶固端约束情况下的变形；其二为墩顶自由情况下的变形。因此可以组合系数来表达(或组合)此类复杂边界条件下的形函数，由此可以假定墩身位移形函数为：

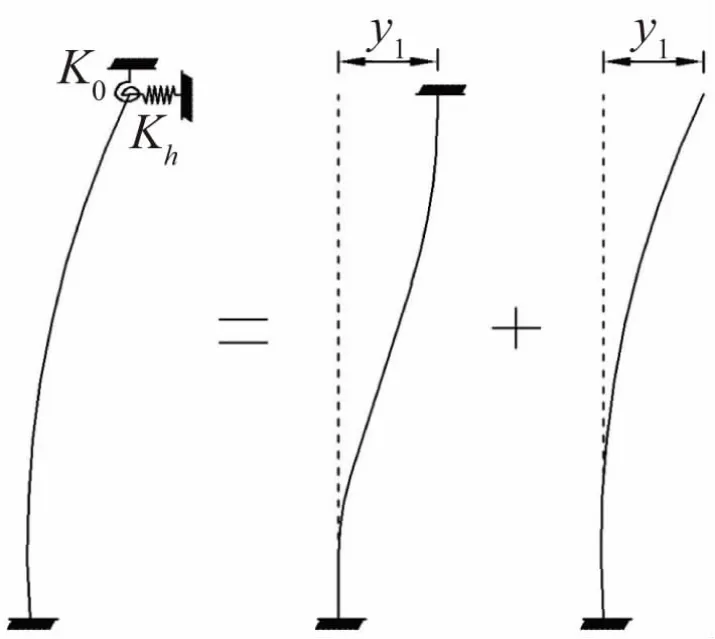
图1 计算模型简图

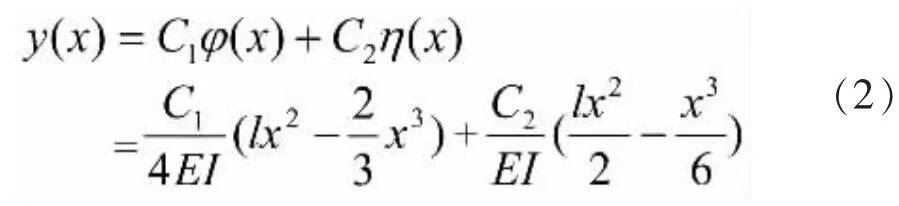
式中：C1、C2为组合系数，由桥墩的变形可知两者必不同时为零；φ（x）、η（x）分别为两端固结，一端固结一端自由的墩身位移形函数，其表达式为：

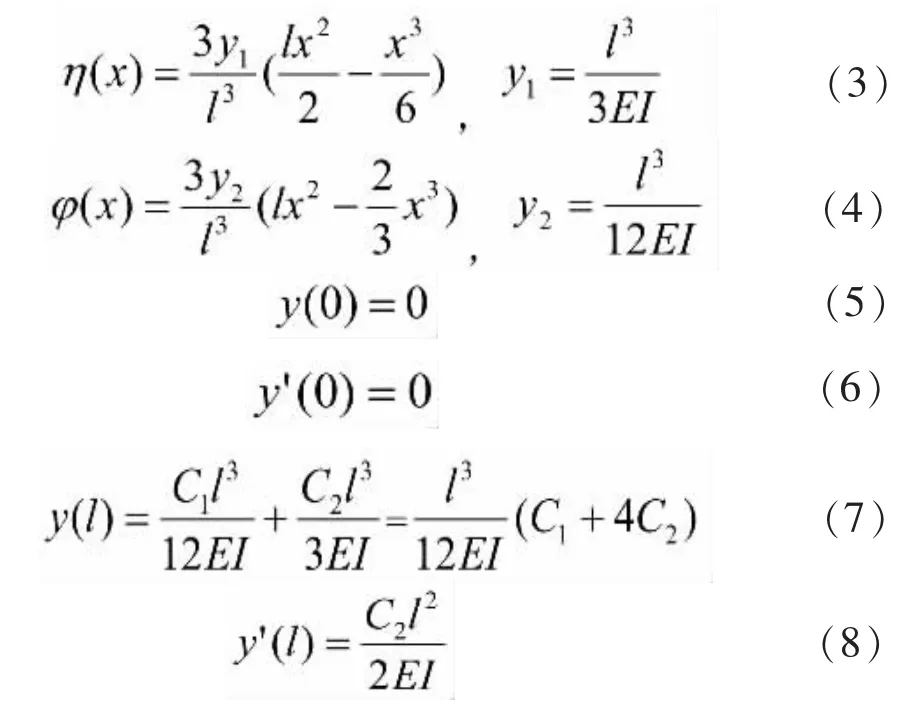
3 变分法求解

对式（2）求导可得式（9）、式（10）：

将式（2）、式（9）和式（10）代入总势能方程（1）并整理得：

方程组有非零解，故C1，C2的行列式值为零：

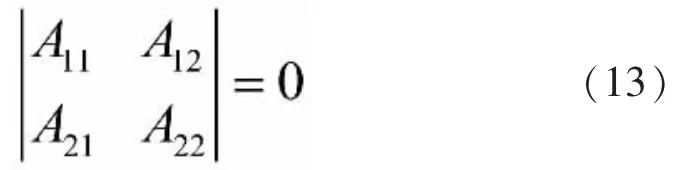
式（12）的展开式即为Pcr的二次代数方程，可求出两个根，其中的最小根即为临界荷载，继而可由欧拉公式解出计算长度。

为了方便计算，利用VC将式（12）编制成计算程序。同时，为验证程序，将墩顶约束刚度置为0，表示墩顶为自由边界，程序计算结果为1.992 5，由04规范规定的理论计算长度系数为2，偏差为0.38%；若将墩顶转动刚度置为无穷大，本文计算结果为0.993 4，其理论计算长度系数为1，偏差为0.65%。由此可见，由式（12）的计算精度满足要求。可用该程序计算刚性地基下墩顶弹性约束时桥墩计算长度值。

4 算例分析

某桥墩高30 m，圆形独柱实心墩，墩径2 m，墩身采用C35混凝土。现假定成桥阶段，墩底为固结，通过计算[7]得到墩顶抗推刚度1 020 kN/m，墩顶转动刚度为4 987 kN/m。

现分别利用有限元程序与能量法计算公式计算出该桥墩的临界荷载，再利用欧拉公式，反算出墩的计算长度系数。采用有限元软件 Midas Civil2010建立桥墩模型，墩底采用一般支承，所有方向均固结，墩顶采用一般弹性支承（6×6耦合弹性支承），对模型进行屈曲分析计算，将其计算结果列于表1，对比分析两者计算结果。有限元与能量法计算结果介于1和2之间，这说了实际边界下的计算长度系数与理想边界条件相差较大。此外，有限元与能量法计算结果相差很小，仅为0.21%。这说明能量法假定的形函数具有足够的精度来模拟墩身变形形状，能量法计算结果可靠。

为了进一步分析对能量法对不同高度桥墩计算结果的准确性，本文对相同边界条件下高度由30～70 m的高墩计算长度系数进行计算，其有限元模型见图2所示，其计算结果列于表1。墩高与计算长度系数的关系曲线和误差变化曲线见图3所示。

由图3和表1，高墩在边界条件相同的情况下，随着墩高的增加其计算长度系数在减小。在墩高为70 m，k值减小至1，可认为此时转动刚度对70 m高墩为无穷大。在墩高一定时，采用有限程序和能量法公式计算得到的高墩计算长度系数相差很小。从而，进一步验证了本文所得公式的准确性。

表1 成桥阶段下30 m、40 m、50 m、60 m和70 m高墩的计算长度系数表

图3 30 m、40 m、50 m、60 m和70 m高墩的计算长度系数曲线图

5 结 论

（1）本文用能量法解决了成桥阶段墩顶非理想边界条件下稳定临界力的求解问题，并通过欧拉公式得到了高墩的计算长度系数。在构造位移函数能较好地模拟桥墩的变形，由此所推导的能量法计算公式，概念明确，简单易行。

（2）通过算例分析可知计算高墩计算长度时，须计入墩顶非理想边界条件的影响。

（3）本文所推能量法公式计算结果同有限元程序接近，精度较高，对公路桥梁常见高桥墩具有普遍适用性，可供设计参考使用。

[1]白青侠，宋一凡.高桥墩几何非线性分析的能量法[J].西安公路交通大学学报，2001，21(2):53-55.

[2]赵明华，刘恩，汪优.桩柱式高桥墩桩基稳定性分析[J].公路交通科技,2008,25(7):95-99.

[3]赵明华，王杜鹃，杨明辉.高墩-群桩体系临界荷载计算[J].湖南大学学报(自然科学版)，2011，（08）.

[4]郭梅.高墩大跨度连续刚构桥稳定性分析[J].西安公路交通大学学报，1999，19(3):31-38.

[5]刘进.高墩大跨连续刚构桥桥墩稳定性分析[J].铁道建筑,2006, 4(10):13-15.

[6]刘进.高墩大跨连续刚构桥桥墩稳定性和静力分析[D].长沙：湖南大学，2004.

[7]程翔云.桩柱式高桥墩几何非线性效应分析的迭代法[J].公路，2003，（19）:60-64.

[8]程翔云.高桥墩设计计算中的两个问题[J].重庆交通学院学报, 2000，（06）:6-10.

U443.22

B

1009-7716（2017）03-0075-03

10.16799/j.cnki.csdqyfh.2017.03.022

2016-11-08

元德壬（1979-），男，广西岑溪人，硕士，工程师，从事公路工程建设管理工作。