美国新轿车的需求影响分析
2017-04-08刘飞宏
刘飞宏
本文在双对数模型的前提下,使用了传统的多元回归方法、主成分分析法等方法,从不同的角度对这个问题进行了分析。同时,本文还借鉴了时间序列的方法来对分析结果进行参照。通过综合比较,从而找出对于这一问题最适用的方法,进而得出在美国这样的成熟市场,环境中的各个因素对于汽车需求量的作用与影响,并做出相应预测。本文从总体上考虑了就业情况、国民收入、消费价格以及贷款利率等因素。它们分别受到企业、个人、政府以及央行的行为影响,是购车需求的主要考量标准。
变量解释
x1新车消费者价格指数
x2城市居民消费者价格指数
x3个人可支配收入(PDI)
x4利率(%),金融公司直接支付的票据利率
x5城市就业劳动力y新轿车销售量
传统模型:多元线性回归
首先,调用sas的reg过程,在传统的多元线性回归的假定下对变量进行回归。
假定:1)解释变量是确定型变量;2)随机误差项具有零均值和等方差性;3)随机误差项满足正态分布。
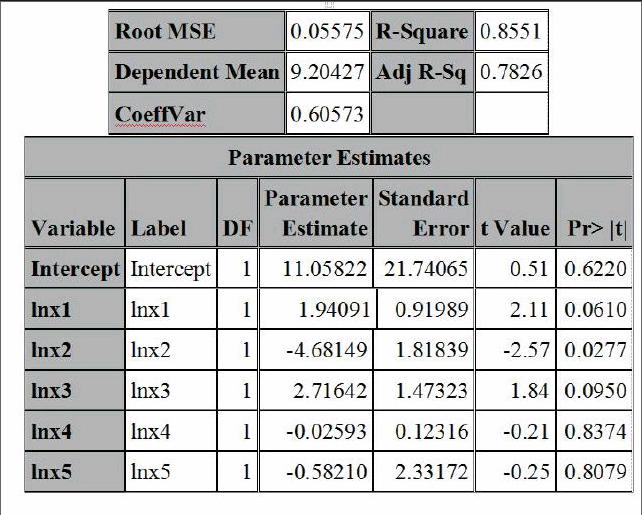
结果如下:
回归方程为:
Lny=11.05822+1.94091lnx1-4.68149lnx2+2.71642lnx3-0.02593lnx4-0.58210lnx5
本文发现只有一个t统计量是显著的,而其他的变量都不显著。不仅如此,城市居民价格指数(x2)的符号为负,而新车价格指数(x1)却为正,与价升量跌的经济学常识不和。收入水平(x3)与就业水平(x5),利息率(x4)无什么显著影响,这说明这个模型有严重的共线性问题。总之现在建立的多元线性回归模型与定性模型相违背,同时存在严重共线性性。需要进一步的改进。
改进模型
一次指数平滑模型。一次指数平滑法是指以最后的一个第一次指数平滑。如果为了使指数平滑值敏感地反映最新观察值的变化,应取较大阿尔法值,如果所求指数平滑值是用来代表该时间序列的长期趋势值,则应取较小阿尔法值。同时,对于市场预测来说,还应根据中长期趋势变动和季节性变动情况的不同而取不同的阿尔法值,一般来说,应按以下情况处理:
如果观察值的长期趋势变动接近稳定的常数,应取居中阿尔法值,使观察值在指数平滑中具有大小接近的权数;
如果观察值呈现明显的季节性变动时,则宜取较大的阿尔法值,使近期观察在指数平滑值中具有较大作用,从而使近期观察值能迅速反映在未来的预测值中;
如果观察值的长期趋势变动较缓慢,则宜取较小的e值,使远期观察值的特征也能反映在指数平滑值中。在确定预测值时,还应加以修正,在指数平滑值s,的基础上再加一个趋势值b,因而,原来指数平滑公式也应加一个b。
一次指数平滑法是根据前期的实测数和预测数,以加权因子为权数,进行加权平均,来预测未来时间趋势的方法。
一次指数平滑法计算公式为:yt+1=axt+(1-a)yt式中,xt——时期t的实测值yt——时期t的预测值a——平滑系数,又称加权因子,取值范围为0≤a≤1。
将yt,yt-1,……y2的表达式逐次代入yt+1中,展开整理后,得:
yt+1=axt+a(1-a)xt-1+a(1-a)2xt-2+…+a(1-a)t-1x1+(1-a)ty1
从上式中可以看出,一次指数平滑法实际上是以a(1-a)k为权数的加权移动平均法。由于k越大,a(1-a)k越小,所以越是远期的实测值对未来时期平滑值的影响就越小。在展开式中,最后一项y1为初始平滑值,在通常情况下可用最初几个实测值的平均值来代替,或直接可用第1时期的实测值来代替。
从上式可以看出,新预测值是根据预测误差对原预测值进行修正得到的。a的大小表明了修正的幅度。a值愈大,修正的幅度愈大,a值愈小,修正的幅度愈小。因此,a值既代表了预测模型对时间序列数据变化的反应速度,又体现了预测模型修匀误差的能力。
在实际应用中,a值是根据时间序列的变化特性来选取的。若时间序列的波动不大,比较平稳,则a应取小一些,如0.1~0.3;若时间序列具有迅速且明显的变动倾向,则a应取大一些,如0.6~0.9。实质上,a是一个经验数据,通过多个值进行试算比较而定,哪个a值引起的预测误差小,就采用哪个。
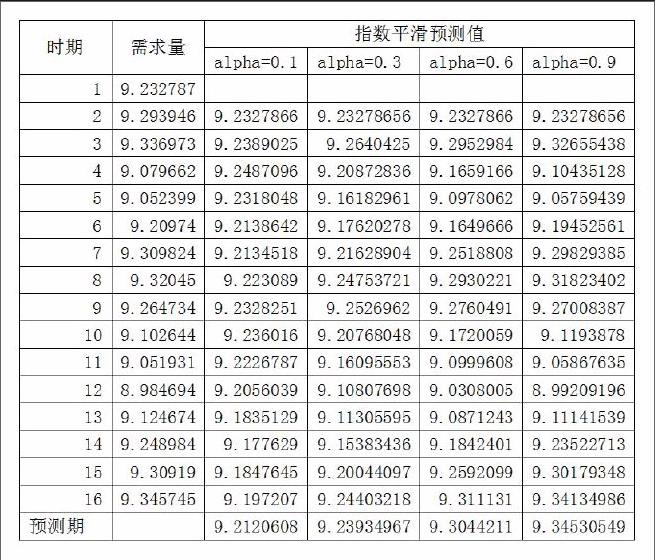
本文分别选取阿尔法值为0.1,0.3,0.6,0.9时,对小汽车需求量进行预测,结果如下表:
分别计算四中预测结果的均方误差,
求得,平滑常数alpha=0.1时,MSE=0.015718;平滑常数alpha:0.3时,MSE=0.007762;平滑常数alpha:0.6时,MSE=0.002651;平滑常数alpha=0.6时,MSE=0.00038,显然,平滑常数alpha=0.9时,所对应的均方误差最小,所以选定0.9作为平滑常数。
ln y17=ax16+(1+α)y16=9.345305
y17=exp(9.3453051=11445
在对影响因素的分析中,本文發现多元线性回归对于影响因素的分析与定性模型最为贴切,解释合理而且拟合优度也较佳。但是在预测的精度上,本文发现简单的时间序列的处理方法反而较回归方法而言更为胜任。这说明回归更善于解释而时间序列的处理更精于预测,在短期的外推中应首先考虑使用时间序列模型。本文认为,从回归的结果来看,城市就业劳动力(x5)对于新轿车需求影响最大,说明就业对于轿车这类的固定资产的购置而言影响程度更大。而在对于下一年的预测中,本文采用时间序列的预测结果,认为新轿车的需求量为11445千辆。