回转式烘干机物料空间运动建模和数值分析

李妙玲，赵红霞，姚永玉

（洛阳理工学院机械工程学院，河南 洛阳 471023）

回转式烘干机物料空间运动建模和数值分析

李妙玲，赵红霞，姚永玉

（洛阳理工学院机械工程学院，河南 洛阳 471023）

目前，回转式烘干机筒体内物料运动方式的研究方法主要是建立扬料板持料、撒料模型及物料在筒体内滞留时间模型，但大多数计算公式过于依靠经验常数，且物理意义不明确。本文以物料空间抛落运行机理为基础，采用数值分析法建立了回转式烘干机内的物料运动模型。首先研究了回转式烘干机内物料的空间运动规律，以位于任意回转位置扬料板翼端点处的物料颗粒为研究对象，建立了物料运动模型，并用Matlab绘图工具箱绘制了物料在筒体内运动状态的三维空间图像。然后，推导了物料在筒体轴向运动距离解析式和以扬料板持物量为权重的滞留时间数值分析模型，这些模型综合考虑了干燥介质推力、筒体倾斜度、转速及填充系数等因素的影响，物理意义明确，与生产实例和文献公式计算结果基本一致。

回转式烘干机；干燥；传递过程；状态方程；数值分析；停留时间

回转式烘干机主要依靠回转筒体内的扬料板带起物料，使抛落状态的物料和热气体在空间充分接触，得到干燥。这种烘干机结构简单、物料适应性强、故障低、操作简单，特别适用于颗粒状物料的烘干，被广泛应用于建材、冶金、轻工、复合肥、粮食、石油化工等行业。烘干机的产量和烘干效率与筒体倾斜度和转速有关，扬料板的形状和布局同样对筒体内物料与热空气交换情况起着决定性的作用，其理论和应用价值已经受到了研究者的重视[1-2]。研究回转式烘干机内物料的运动模型，对于优化回转筒体和扬料板结构、提高传热效率、促进回转式干燥机的应用和发展有着重要意义[3]。

回转筒体内物料的主要运动包括被扬料板带起物料的空间抛落运动和筒体壁上滞留物料的翻滚运动。烘干作用主要依靠物料与热风接触实现，即尽可能地使抛落运动中的物料充满筒体内部空间，因此烘干效果主要决定于回转筒体内扬料板的结构和安装方式[4-6]。同时，受筒体倾斜、干燥介质推力等因素的综合影响，使物料沿回转筒体轴向的运动机理变得复杂，直接影响了转筒内物料的停留时间[7]。

目前，国内外对回转式烘干机的研究已经取得了一些有价值的研究成果[8-10]，通常是通过建立扬料板持料、撒料模型及物料在筒体内的滞留时间模型研究物料运动规律，揭示烘干过程中的传质传热机理。但大多数计算公式过于依靠经验常数，且物理意义不明确。本文以物料空间抛落运行机理为基础，建立物料运动的数值分析模型，推导以扬料板持物量为权重的物料滞留时间公式，并将其在工业应用中进行检验。

1 物料运动建模

转筒内扬料板带起的物料做空间抛落运动，抛落运动使物料与热风充分接触，是物料干燥的主要运动。筒体倾斜、干燥介质推力、转筒内扬料板的结构等因素综合影响着物料的抛落状态和在筒体内的滞留时间。

如图1所示，回转式烘干机转筒以水平倾角λ安装，筒体半径为R，回转角速度为ω，升举扬料板翼端点的回转半径为r。假设颗粒物料在升举阶段只作圆周运动，没有沿转筒壁的滚动。在某一时刻t，位于扬料板翼端点P0的物料颗粒被抛出，初始速度v0=ωr，选择图1所示坐标系，受力平衡方程为式(1)。

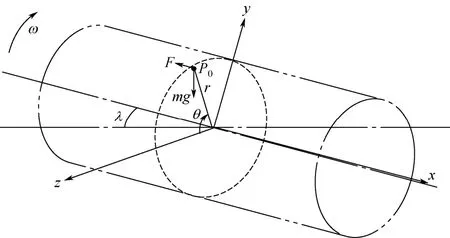
图1 回转式烘干机物料受力状态图

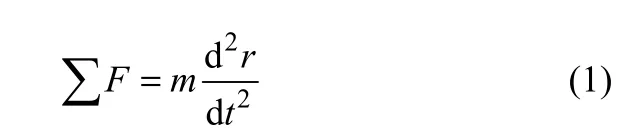
在图1所示的坐标系中，式(1)在x、y、z坐标轴上的投影分量见式(2)。

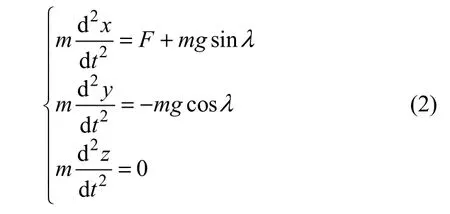
式中，m表示抛落物料质量，kg；λ为回转筒体的倾角，(°)；g为重力加速度，9.8m/s2；F为干燥热气体对空间运动物料的作用力，kgf，逆流时F为负值，1kgf=9.80665N。

如图1所示，令扬料板翼端点P0与z轴正向的夹角为θ，物料颗粒从该位置开始撒落，令t=0，可知初始抛落条件见式(3)。

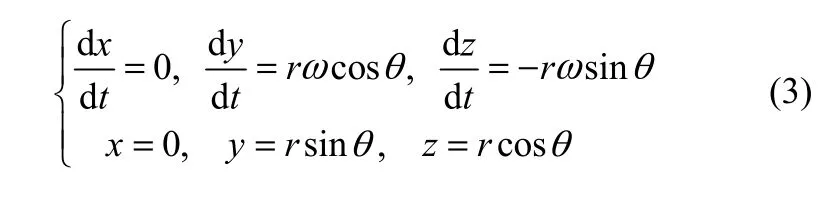
联立式(2)、式(3)，解得为式(4)。

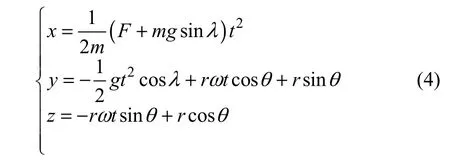
当物料下落到扬料板翼端点所在圆周时，完成一个撒料周期。此时有式(5)。

联立式(4)和式(5)，解得物料撒落时间为式(6)。

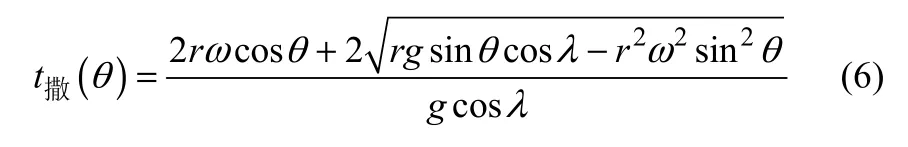
由式(6)知，物料撒落时间是扬料板位置角的函数。

理想情况下，扬料板从θ=0°开始撒料，直至θ=180°物料全部抛撒完毕。假定扬料板撒料边缘的回转圆周半径1.3m，在一个撒料周期中，物料的空间运动轨迹用Matlab绘图工具箱绘制如图2所示。图中粗实线表示物料的运动轨迹，细实线表示扬料板撒料边缘的回转圆周。图2(a)为三维空间运动轨迹，图2(b)为在回转圆周横截面（yz）面上的轨迹投影。此为理想状况下物料在筒体内的分布状态，即整个筒体内形成了均匀的料幕。

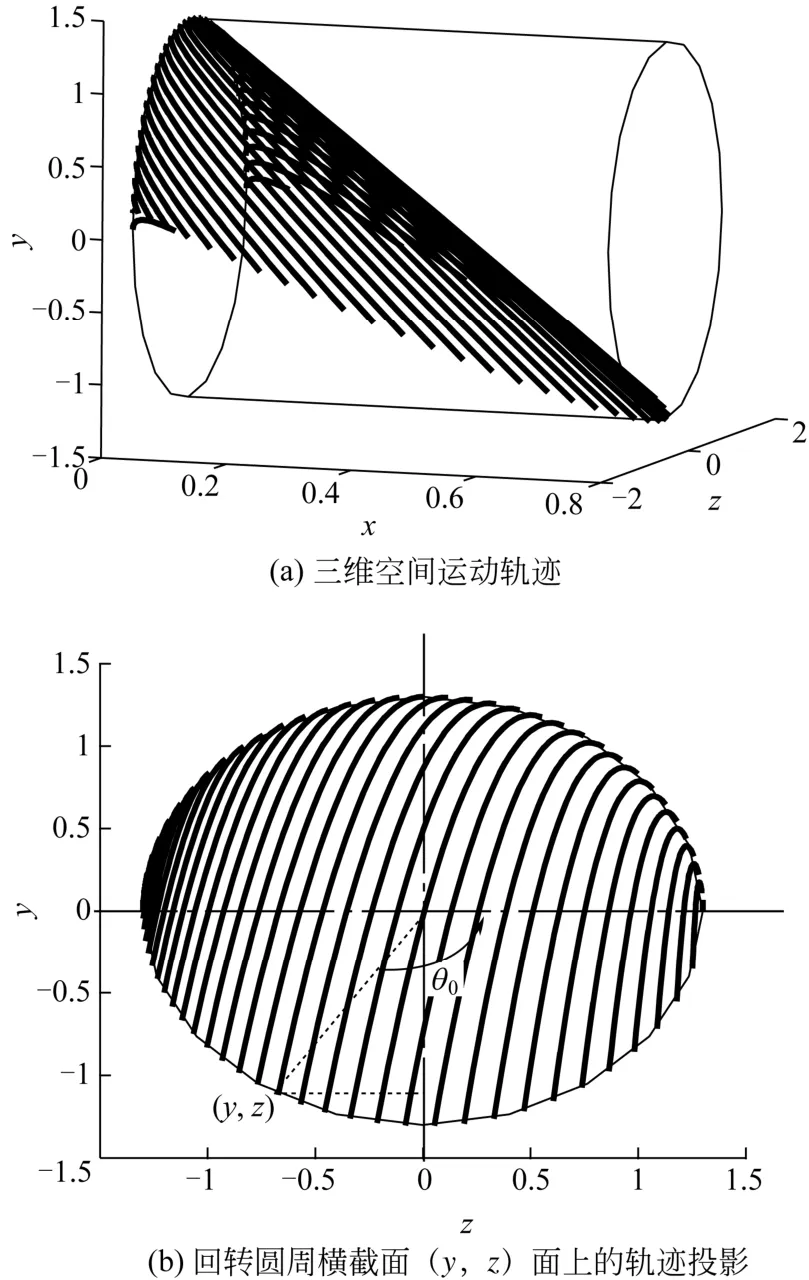
图2 物料的运动轨迹示意图

由图2可知，物料落点位置角度见式(7)。

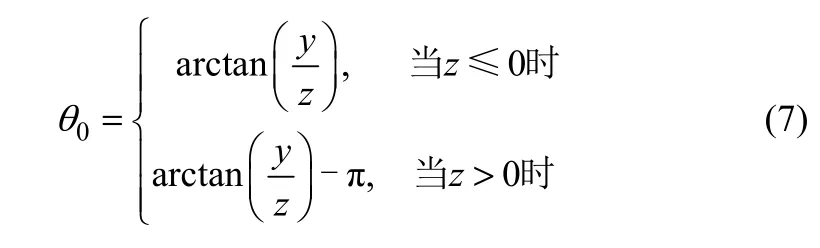
但是，物料的特性、扬料板的形状、安装角度等因素都影响着物料的洒落状态，通常在转筒旋转角θ未到达180°时物料即洒落完毕，这就造成了实际应用中经常发现的“风洞”现象，导致热风的短路，降低传热效率。

如图3所示，在回转式烘干机的工作过程中，物料被扬料板从转筒下部搅起。随着筒体的旋转，扬料板夹带着物料逐步上升，堆积在扬料板上的物料即开始从扬料板翼端点滑落下来，形成料幕。扬料板后部的物料不断地补充到扬料板翼端点，在重力和离心力的作用下以一定速度下落，形成连续的抛物线形料幕。同时，扬料板的物料持有量减少。

料幕分布范围及其均匀程度，将是判定烘干机工艺性能优劣的主要指标[11]。事实上，物料的特性、扬料板的形状、安装角度、烘干机转速等因素都影响着物料的洒落状态。可能当扬料板越过图3中的水平面后，即起始扬料角θ1＞0°，仍然没有开始撒料，造成了实际应用中经常发现的“风洞”Ⅰ；或扬料板未旋转到另一侧水平面，即终止扬料角θ2＜180°时，物料即洒落完毕，形成了“风洞”Ⅱ。“风洞”的大小决定于扬料板扬起料幕的分布范围，即扬料板翼端点开始撒料和撒料结束的位置角度范围。

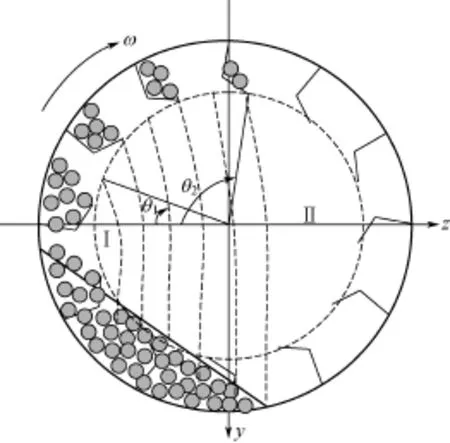
图3 扬料板持物量状态和转筒内物料的运动状态（实际应用中的“风洞”现象）

2 物料轴向运动和滞留时间数值分析

转筒工作时，物料不断被扬料板升举、洒落，是一个重复的运动过程。物料颗粒在气流中飘落到转筒底部的同时，沿转筒轴线方向向前移动一段距离，完成一个抛撒周期[12]。由于物料的抛落运动是主要烘干阶段，总是希望物料尽可能的处于抛落状态，以满足抛落到达筒体底部的物料颗粒同时再一次被扬料板抄起。

设单块扬料板最大持物量W(θ1)，若扬料板转过Δθ角，将有ΔW(θ)的物料量被撒落。若以扬料板散落物料量为权重，则单块扬料板扬起的物料沿筒体轴向移动的距离见式(8)。

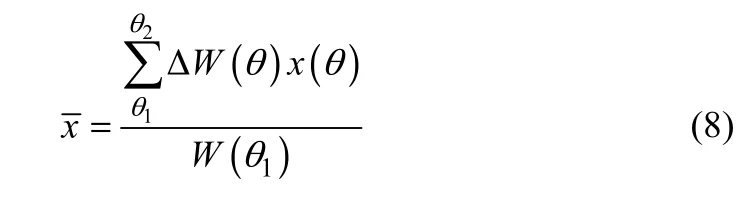
物料抛落到筒体下壁后，重新被升举，物料即随筒体作圆周运动，直至被撒落。若烘干机转速为n（单位为r/min），升举阶段物料随筒体回转运动平均时间（单位为s）为式(10)。

根据扬料板的安装密度和安装方式，分别计算各阶段物料的运动时间和轴向位移，再总和成物料在转筒内的滞留时间和总位移。

若回转筒体总长为L，物料在筒体内经历的扬料次数为式(11)。

一个扬料周期内，物料的平均滞留时间为式(12)。

则物料在回转筒体内的总滞留时间为式(13)。

任意时刻t，物料在回转筒体中的轴向位置为式(14)。

3 验证和分析

以某水泥厂正在使用的φ2.6m×20m直接加热逆流回转式烘干机为例，生产率9500kg/h。该烘干机烘干物料为水泥原料，平均粒径10mm，颗粒密度2×103kg/m3，堆密度0.8×103kg/m3，物料休止角为35°；干燥介质为热空气，密度0.98kg/m3，流速2m/s，运动黏度约1.2×10–5m2/s；筒体安装倾斜角5°，周向均布L型扬料板，两边长和夹角分别为0.26m、0.13m和90°，安装角度80°。

工作载荷下，筒体填充系数为15%，转速4r/min。物料和产品的含水率分别为8%和0.5%。

理论起始扬料角0°，扬料终止角120°。利用本文建立的数值模型对各运动参数进行计算。结果如下：单块扬料板扬起的物料沿筒体轴向移动距离为0.125m，物料在筒体内经历的扬料次数为160次；一次扬料周期约4.6s，物料在筒体内滞留时间约12min。

该结果比现场实测值大1～1.5min，通过现场观察和分析，其原因在于以下方面：

（1）物料下落过程中发生相互碰撞，增加下落时间；

（2）小颗粒物料受到热风吹动呈现出悬浮现象，烘干机工作时间越长，悬浮物料浓度增加，逆流风的作用力被削弱；

（3）物料落在筒体底部，与滞留物料表面接触，由于下落惯性，有继续向筒体旋转反方向翻滚的趋势，延缓了圆周运动的开始时间。

本验证实例中，扬料板高度设置符合“一般为筒体直径的1/8～1/12”的常规标准，物料填充系数15%为常规取值的下限。滞留时间计算结果乘以修正系数0.9，更为符合实际情况。

为了进一步验证本文公式计算结果，将其和文献公式进行比较。文献[3]中给出了滞留时间（单位为min）经验公式见式(15)。

式中，α表示物料休止角，(°)；L表示筒体长度，m；D表示筒体直径，m；n表示筒体转速，r/min；λ表示筒体安装倾斜角，(°)。

根据式(15)计算物料滞留时间约为8.6mm，但该经验公式是无物理量、使用颗粒均匀的物料，在无扬料板或挡圈的圆筒内进行试验得出的，与各种回转式干燥机的实际情况差别较大。扬料装置等会使物料的移动速度变慢，增加物料滞留时间。根据该公式的计算结果需要用经验系数进行修正。

文献[9,13]给出的滞留时间（单位为min）模型为式(16)。

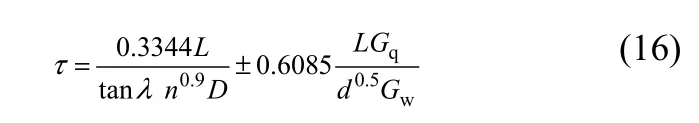
式中，d表示物料颗粒直径，μm；Gq表示气体速度，kg/(m2·s）；Gw表示物料速度，kg/(m2·s）；其他符号意义同式(15)。逆流时取+，顺流时取–。

根据式(16)计算物料滞留时间为10.7mm。该公式将转筒的转速、倾斜度、物料和气体的流向以及烘干机产量、气体流速等因素考虑在内，较为全面地反映了物料的运动状态。但该公式物理意义不够直观，式中经验系数多，应用范围受到局限。

利用本文建模方法计算结果和公式(16)结果接近，相差1.3min，等于乘以修正系数后的结果。因此本文推导公式具有合理性，且物理意义明确。

本文数值模型没有考虑物料填充率、物料休止角的因素影响，因此对于筒体内滞留料层高度导致的物料沿筒体轴向运动迟滞现象不能量化分析，滞留时间计算结果的系数仍然要收集大量的数据。

实际应用中为了保证烘干效果，生产厂家大多推荐增加回转式烘干机筒体长度、减小筒体安装倾斜角、减小筒体转速，因此物料填充率通常不大于25%，滞留料层高度与15%填充率时相差约10cm，故由填充率导致的物料运动迟滞现象变化不大。

4 结论

回转式烘干机中物料的空间抛落运动是物料与热风充分接触，实现干燥的重要步骤。本文研究了回转式烘干机内物料的空间运动规律，建立了物料在筒体内的运动解析模型和滞留时间数值分析模型。通过对物料的轴向和周向运动分析，获得了理想的物料运动路线，并用三维空间图像方式展示了物料在筒体内的运动状态。本文建立的滞留时间数值分析模型综合了筒体倾斜度、干燥介质推力、筒体转速、筒体填充系数等因素的影响。经实际应用实例验证，并与文献经验公式对比，本文推导公式合理，且物理意义明确。

[1]祝水琴，蔡建良. 复合肥干燥机组合式抄板的设计及应用[J]. 化工机械，2008，36（5）：303-305. ZHU S Q，CAI J L. Design and application of the assembled lifting flights in the dryers for compound fertilizers[J]. Chemical Engineering & Machinery，2008，36（5）：303-305.

[2]张立栋，李少华，余侃胜，等. 油页岩与固体热载体在回转干馏炉内混合特性的冷态实验[J]. 化工进展，2011，30（3）：492-497. ZHANG L D，LI S H，YU K S，et al. Cold experiments on mixing performance of oil shale particle and solid heat carrier in rotary retorting[J]. Chemical Industry and Engineering Progress，2011，30（3）：492-497.

[3]刘广文. 干燥设备设计册[M]. 北京：机械工业出版社，2009： 721-727. LIU W G. Ganzao shebei sheji shouce[M]. Beijing：China Machine Press，2009：721-727.

[4]李坦平，才世杰. 回转式烘干机扬料板截面形状的理论推导与应用[J]. 新世纪水泥导报，2001（2）：31-32. LI T P，CAI S J. Theoretical derivation and application of lifting plate section in a rotary dryer[J]. Cement Guide for New Epoch，2001（2）：31-32.

[5]马晓录，张勇. 转筒干燥机活动折弯抄板设计方法研究[J]. 河南工业大学学报（自然科学版），2013，34（5）：91-95. MA X L，ZHANG Y. Design method of movable bending flights in rotary dryer[J]. Journal of Henan University of Technology（Natural Science Edition），2013，34（5）：91-95.

[6]张扬. 连续炒籽机流场数值模拟及扬料板结构优化[D]. 汉中：陕西理工学院，2016. ZHANG Y. Numerical simulation of continuity fried seeds machine and throwing plate structure optimization[D]. Hanzhong：Shaanxi University of Technology，2016.

[7]SHAHHOSSEINI S H，SADEGHI M T.，GOLSEFATAN H R. Dynamic simulation of an industrial rotary dryer[J]. Iranian Journal of Chemical Engineering，2010，7（2）：68-77.

[8]赵改菊，吴静，尹凤交，等. 转筒干燥器中物料运动模型的研究现状[J]. 化工机械，2009，36（3）：190-195. ZHAO G J ，WU J ，YIN F J，et al. Research status of the solids transportation models in flight rotary dryers[J]. Chemical Engineering & Machinery，2009，36（3）：190-195.

[9]LISBOA M H，VITORINO D S，DELAIBA W B，et al. A study of particle motion in rotary dryer[J]. Brazilian Journal of Chemical Engineering，2007，24 （3）：365-374.

[10]黄志刚. 转筒干燥器中颗粒物料流动和传热传质过程的研究[D].北京：中国农业大学，2004. HUANG Z G. Study on partieulate materials flow and heat and mass transfer in rgtary dyers[D]. Beijing：China Agricultural University，2004.

[11]王文山. 试论回转式烘干机扬料板扬料程序及其它[J]. 水泥，1990（11）：14-18. WANG W S. Discussion on feed procedures of lifting plates and others for a rotary dryer[J]. Cement，1990（11）：14-18.

[12]韩福东. 关于回转烘干机扬料板尺寸计算问题的探讨[J]. 水泥，1992（5）：39-40. HAN F D. Discussion on calculation of lifting plate sizes for a rotary dryer[J]. Cement，1992（5）：39-40.

[13]FRIEDMAN S J，MARSHAL W R. Studies in rotary drying：Part I. Hold-up and dusting[J]. Chemical Engineering Progress，1949，45（8）：482-573.

Estimation models and mathematical analysis of particle transportation in a rotary dryer

LI Miaoling，ZHAO Hongxia，YAO Yongyu
（School of Machnical Engineering，Luoyang Institute of Science and Technology，Luoyang 471023，Henan，China）

At present，the research method of material movement in the cylinder of a rotary dryer is mainly to set up the held and thrown material models of a lifting plate and the residence time model of materials in the cylinder body. But the most formulas depend too much on the empirical constants，and the physical meaning is not clear. Based on the thrown movement law of materials，the space model of the particle transportation in a rotary dryer is established. First，the motion rule was studied for the solids in the flight rotary dryer. The paths of fall of the particles in the drum were drawn by Matlab drawing toolbox and showed on the three-dimensional image. Then，the analytic mathematical models of the motion were proposed for the space particle. The equations of residence times were deduced. The proposed estimation models were determined by considering the air drag on the solids in the drum，as well as the inclined angle，the rotation speed and the filling rate of a drum. The calculation formula of residence times was with a clear and definite physical meaning. The residence time calculated by using the proposed equation was compared to the average experimental values from the engineering example and the results obtained by calculations using equations proposed in the literature. The equation proposed for predicting residence time generated accurate estimations.

rotary dryer；drying；transport processes；equation of state；numerical analysis；residence times

TH113

A

1000–6613（2017）04–1187–05

10.16085/j.issn.1000-6613.2017.04.005

2016-08-25；修改稿日期：2016-11-01。

全国建筑材料行业科技创新计划项目（2015-M1-2）。

及联系人：李妙玲（1970—），女，博士，副教授，研究方向为建材材机械设计与数值分析、无机非金属材料。E-mail：miaolingli1970@163.com。