结合具体情况 测算圆锥体积
2017-04-07相辉
小学生学习指导(高年级) 2017年5期
◎相辉
结合具体情况 测算圆锥体积
◎相辉
有关圆锥体积的测算,要结合实际情况选择合适的方法,灵活进行解答。例如:
1.转一转求体积
【例1】一个直角三角形的两条直角边的长度分别是6厘米和8厘米,以其中一条直角边为轴,将这个三角形旋转一周,得到一个圆锥,这个圆锥的体积最大是多少立方厘米?
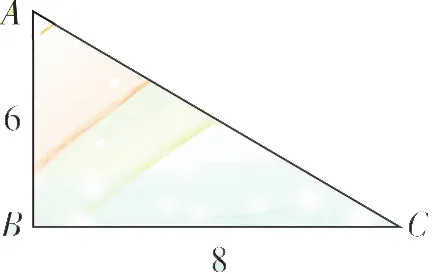
【分析与解】
因为有两条直角边,所以旋转一周后会得两个不同的圆锥。以直角边AB为轴旋转时,AB就是圆锥的高,BC就是圆锥的底面半径;而以BC为轴旋转时,BC就是圆锥的高,AB就是圆锥的底面半径。

所以,以AB为轴旋转时所得到的圆锥体积最大,是401.92立方厘米。
2.切一切求体积
【例2】一个圆锥体,从顶点到底面直径垂直切开,表面积增加了12平方厘米。已知这个圆锥的高是3厘米,它的体积是多少立方厘米?
【分析与解】

3.比一比求体积
【例2】一个圆柱和一个圆锥底面半径相等,圆柱的高是圆锥的高。圆柱的体积是24立方厘米,圆锥的体积是多少立方厘米?
【分析与解】
乍一看这道题目,似乎不好解答。因为缺少圆锥的底面半径和圆锥的高,而且也不容易求出底面半径和高,所以运用公式无法直接求出圆锥的体积。我们不妨换个角度,如果知道了和这个圆锥等底等高的圆柱体积,就可以运用它们之间的关系,求出这个圆锥的体积。
解决与圆锥相关的实际问题一般要借助圆锥的特征、圆锥的底面积和圆锥的体积计算公式。有时还可以借助一些其他方法,如圆锥和圆柱体积之间的关系、假设等思维方法,才能使问题解决的过程变得轻松简单。
