基于LM方法的双指数跳扩散模型的参数估计
2017-04-05吕韩,陈萍
吕 韩,陈 萍
( 南京理工大学 理学院,南京 210094 )
基于LM方法的双指数跳扩散模型的参数估计
吕 韩,陈 萍
( 南京理工大学 理学院,南京 210094 )
介绍了双指数跳扩散模型的特征,阐述了Lee-Mykland方法识别跳跃的基本思想,用极大似然法对参数进行估计,从而形成了一种新的组合方法。利用上证指数2010—2016年的历史数据进行实证分析,实验结果表明:使用组合方法对收益率时间序列数据进行估计,不但能有效估计跳扩散模型的参数,而且能把跳跃发生的时点和相应的参数识别出来。
双指数模型;Lee-Mykland方法;上证指数;跳跃识别
绝大多数研究都将标的资产价格假设为几何布朗运动,认为资产的价格关于时间是连续函数,资产的价格变动也是连续的。作为期权定价基石的Black-Scholes[1]模型,在一定的假设前提下解析出了金融衍生产品的定价公式,并因其简单、易理解等优点被广泛应用。由于模型的高度理想化,实际市场的两个现象受到很大的关注:① 非对称的尖峰肥尾特征,即资产回报分布是有偏的,并且有比正态分布更高的峰度和更厚的尾部;② 波动率“微笑”,BS模型假设隐含波动率是常量,而实际上,金融市场上得到的隐含波动率曲线是像一个“微笑”的曲线,也就是意味着它是执行价格的凸函数。
人们一直试图放松BS模型的种种假设,来解释尖峰现象和波动率“微笑”。其中最重要的方向之一,就是在扩散过程的基础上引入跳跃,以更好地描述标的资产所服从的随机过程。当市场中有重大信息(如突发事件、自然灾害、政策大调整等)到达时,市场股价可能发生间断性的“跳跃”过程,在实际市场中上,标的资产的价格会出现“不正常”的振动。此时,利用几何布朗运动再来描述资产收益变动过程就不是很合理了。为了刻画股票价格变动的这种非连续行为,研究者们提出了很多模型加以解释,跳扩散模型[2]就是其中较为重要的一种。研究结果表明:跳跃扩散过程描述股价运动要优于布朗运动,已逐渐地被应用在期权定价及汇率、利率的突变研究等方面[3-4]。
股价行为建模作为目前研究的热点问题,对资产定价、投资组合以及产品设计都有决定性意义。从目前的文献可以看出:中国股市收益率分布特征的研究已是相当丰富,但是对于股价的运动规律,尤其是其中跳跃成分的探讨还是一个鲜有人涉足的领域。本文利用Lee和Mykland提出的跳识别方法,结合极大似然估计,对双指数跳扩散模型的参数估计方法进行研究,对于扩充现有模型理论、寻求资产价格变动规律、评估衍生品的风险特征等都具有一定的现实意义。
1 双指数跳扩散模型
S.G.Kou[5]在总结前人模型的基础上,提出双指数跳跃扩散模型。模型的基本假设为:资产动态服从布朗运动加上复合泊松过程,其跳跃幅度服从Laplace双指数分布。为了便于参数估计时的数值计算,假设Kou提出的模型中p=q,记St为t时刻的股票价格,满足如下模型:
(1)
其中:μ是漂移率;σ是波动率; dWt是一个服从标准Brown运动的增量;Ju和Jd分别表示向上和向下的跳跃幅度,皆服从指数分布。密度函数表达式分别为:
(2)
(3)
ηu(ηd)表示向上(下)跳跃幅度的均值,dNu(λu)(dNd(λd))表示强度为λu(λd)的泊松计数过程,有p(dNi(λi)=1)=λidt,p(dNi(λi)=0)=1-λidt,i=u,d。由此可见,依方向将“跳”分成了两种类型,服从不对称的对数指数分布。
利用伊藤引理[6]对(1)式进行对数变换后,得到如下形式:
(4)
用Euler方法[7]对模型进行离散化处理,得到t时刻的收益率:
(5)

所以,在Δt→0时,以上收益(5)可以近似为:
(6)

(7)
2 跳的识别与模型的参数估计
由于跳的存在,极大似然估计等传统的模型参数估计方法存在较大的估计误差。针对这个问题,学者提出了马尔可夫链的蒙特卡洛模拟方法(MCMC),在估计跳扩散模型参数问题中得到了广泛应用[8-9]。MCMC方法是从总体上对参数进行估计,无法将跳变序列和连续序列分离识别,因而无法估计跳变时刻和跳跃幅度。
2.1 Lee-Mykland跳识别理论及算法
Lee和Mykland[10]提出了一种跳识别方法,即Lee-Mykland逐时点检验方法,此方法能检测某个给定的收益率数据是否服从纯粹连续分布,从而识别出过程中的跳。主要思想是:先确定一个窗口大小K,在检验给定时刻前选择K个数据,计算最大变动幅度,并与需要检验时刻的价格变化幅度进行比较,如果需要检验时刻的变化幅度超过最大变动幅度则说明这个点为跳。最后依次将窗口后移,逐个时刻检验是否存在跳。Lee和Mykland用价格的时点方差对价格改变量进行标准化构造,得出服从标准正态分布的跳检验统计量。关键是要估计出时点方差。他们采用现实双幂变差为基础来估计时点方差,并且证明了当时间间隔趋于0时,检验误判和漏判的概率趋于0。基于以上思路,他们构造了检验统计变量L(i) 来测试在ti时刻是否存在从ti-1到ti的跳:
(8)
其中
(9)
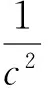
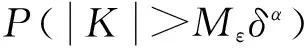
Lee和Mykland给出了跳识别的拒绝域,并证明了若在时间间隔(ti-1,ti]内不存在跳,则在Δt→0 时有:
(10)


下面给出了股票价格收益率序列的跳跃识别算法:
1) 对第i个股价收益率数据用式(8)和(9)计算统计变量L(i)。
2) 选择一个显著性水平α计算阈值,这是一个累计分布函数,满足P(ψ≤β*)=exp(-e-β*)=1-α。


2.2 参数估计方法

1) 跳跃频率的估计
对于强度为的Poisson计数过程来说,对其频率的估计可以用极大似然法估计:
(11)
其中ξ1,ξ2,…,ξn为样本点。
假设1年有250个交易日,则跳跃频率的年估计值为:
(12)
2) 跳跃幅度的估计

(13)
其中x1,x2,…,xn为样本点。
(14)

(15)
3) 扩散过程参数估计
正态分布的均值与方差的极大似然估计分别为:
(16)
(17)
(18)
3 上证指数的实证分析
本文将股票价格描述为一个带有指数跳的扩散过程。为了有效地估计跳跃的频率和幅度,以便预测未来价格。选择上证指数总共4 001个样本(n=4 001),采用本文提出的组合方法来估计模型的参数,并在Matlab中实现以上算法[11]。图1为原始样本数据序列,即2000—2006年上证指数走势。

图1 上证指数走势
由于原始数据波动性较大,使得数据不够稳定,因此对原数据取对数,这样既不会改变数据的相关性又能使原始数据变得相对平稳。然后用
Ri=lnSi-lnSi-1
(19)
得到上证指数的收益率序列。图2给出了样本数据收益率的时间序列图。

图2 上证指数收益率的时间序列图
从图2可以明显看到,股指收益率原始数据图并不平稳,在多个地方存在跳跃点。下面观察收益率序列Rt的基本统计特征。
在Matlab中计算得到收益率数据基本统计量,见表1。

表1 收益率数据基本统计量
从表1可以看出:收益率数据的偏度为-0.339 5,呈现出左偏;峰度系数为7.354 3,大于正态分布峰度系数3,说明股指收益率序列呈现出尖峰厚尾的特征。数据表明,“跳”的存在使得原始数据收益率并不服从正态分布,出现异常点,呈现尖峰厚尾的特征。

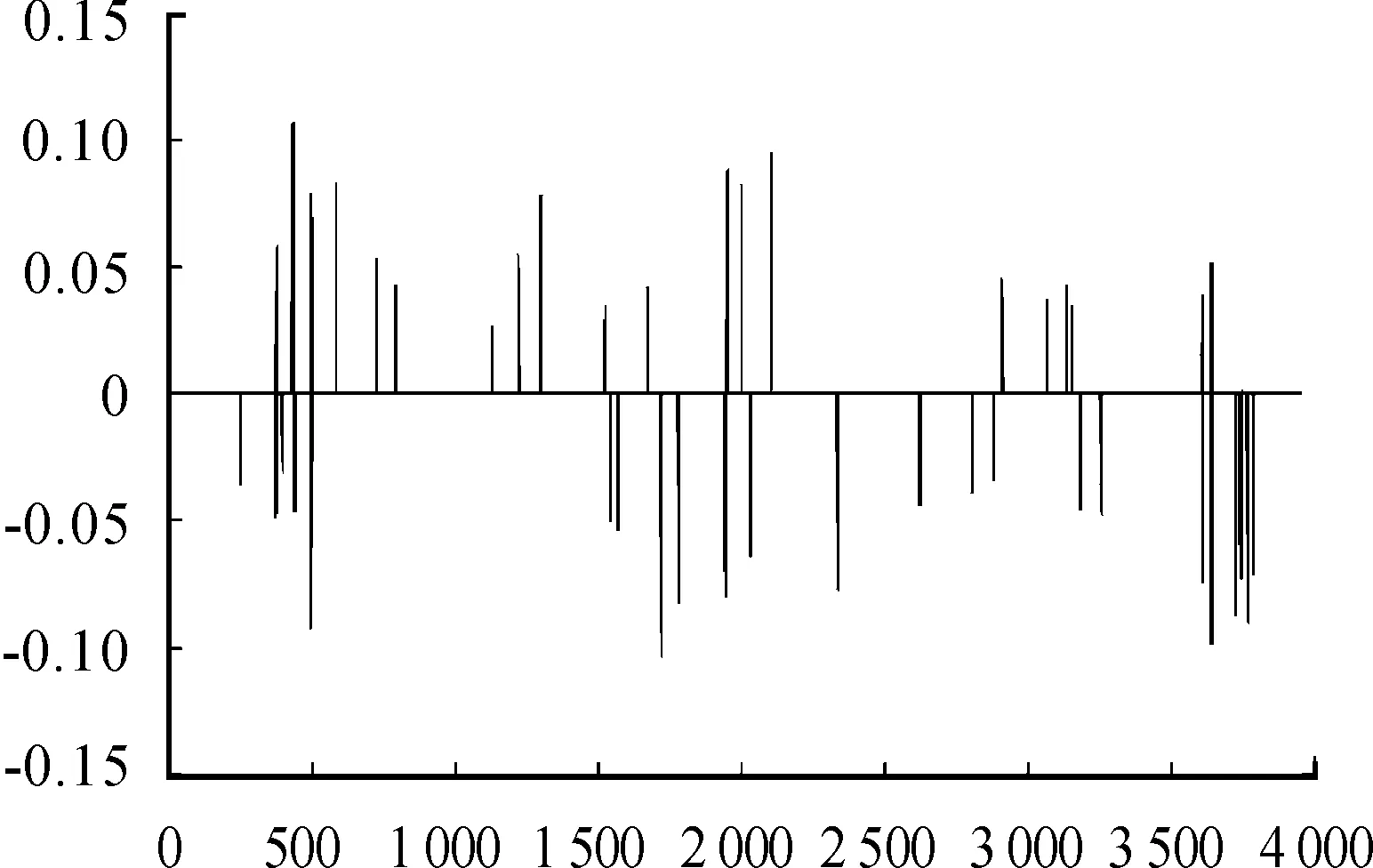
图3 跳辨识结果
用跳跃点前后6个数据来取代跳跃点的收益率,得到修正后的连续扩散过程收益率序列Rt′,根据其与原始数据之差统计出向上跳跃发生次数为24次,向下跳跃次数为28次,跳跃时间如表2、3所示。
图4给出了修正后的收益率序列Rt′的时间序列图。
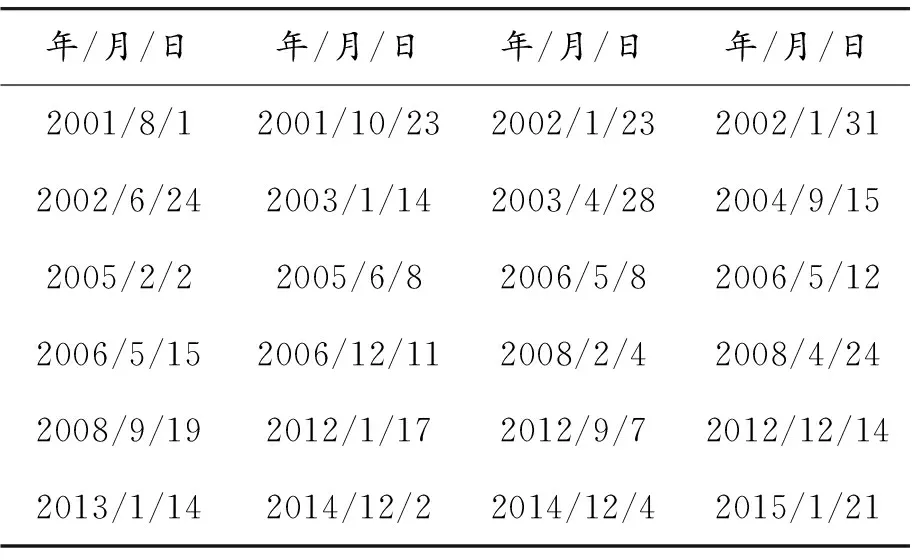
表2 上证指数向上跳跃时间点汇总

表3 上证指数向下跳跃时间点汇总

图4 修正后的收益率序列图
表4给出了修正后的收益率序列的基本统计量。

表4 修正收益率数据基本统计量
由图4可见:修正后的收益率基本平稳,通过和图2的原始收益率序列对比,发现Lee-Mykland跳辨识方法确能很好地辨别出跳跃点。观察表4修正后的收益率序列的统计特征发现:其偏度从-0.219 1变为-0.064 3,左偏程度明显减弱;峰度也从7.594 2降为4.237 9,更加接近正态分布的峰度值3。
在完成了跳的识别工作后,根据本文的极大似然方法估计出收益率序列的参数,估计结果见表5。
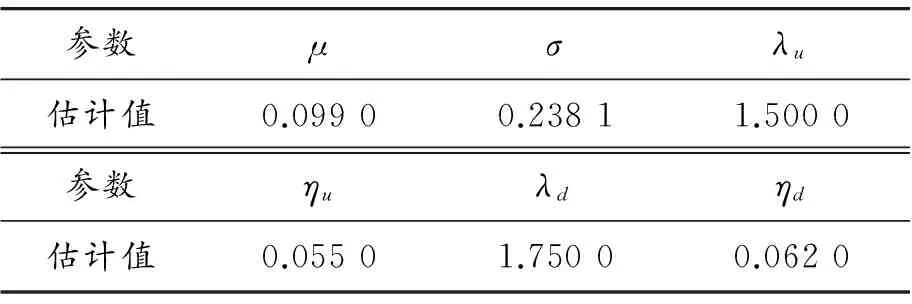
表5 跳扩散模型参数估计结果
从参数估计结果可以看出,收益率序列的年波动率为23.81%,这与实际数据的较高波动性相吻合。向上跳跃和向下跳跃的年频率分别为1.500 0和1.750 0,而跳跃的幅度相仿。
以上完成了上证指数跳扩散模型跳的辨识和参数估计工作,下面对将方法的有效性进行检验。由本文模型(1)和由历史数据估计的参数(表5),采用蒙特卡洛模拟方法生成模拟收益率数据图,通过与真实值(观测值)进行对比来检验估计方法的有效性。根据
(20)
将表5中的参数代入,在Matlab中利用蒙特卡洛方法模拟出相应的收益率数据序列,并生成模拟数据和真实数据的Q-Q图,如图5所示。

图5 上证指数模拟数据与真实值的Q-Q图
从真实值与模拟数据的Q-Q图可以看出,本文建立的双指数跳扩散模型的拟合值和真实值几乎位于一条直线,说明该模型模拟出的数据与真实数据的分布情况拟合效果很好。
4 结束语
[1] BLACK F,SCHOLES M.The pricing of options and corporate liabilityes[J].The journal of political economy,1973(2):637-654.
[2] MERTON R C.Option pricing when underlying stock returns are discontinuous[J].Journal of financial economics,1976,3(1/2):125-144.
[3] CHEN S W,SHEN C H.GARCH,jumps and permanent and transitory components of volatility:the case of the Taiwan exchange rate[J].Mathematics and Computers in Simulation,2004,67(3):201-216.
[4] AKGIRAY V,BOOTH G G.Mixed diffusion-jump process modeling of exchange rate movements[J].The Review of Economics and Statistics,1988(3):631-637.
[5] KOU S G.A jump-diffusion model for option pricing[J].Management science,2002,48(8):1086-1101
[6] SHREVE S E.Stochastic calculus for finance II:Continuous-time models[M].[S.l.]:Springer Science & Business Media,2004.
[7] ACHDOU Y,PIRONNEAU O.Computational methods for option pricing[M].[S.l.]:Siam,2005.
[8] CHIB S,NARDARI F,SHEPHArd N.Markov chain Monte Carlo methods for stochastic volatility models[J].Journal of Econometrics,2002,108(2):281-316.
[9] ERAKER B.Do stock prices and volatility jump Reconciling evidence from spot and option prices[J].The Journal of Finance,2004,59(3):1367-1403.
[10]LEE S S,MYKLAND P A.Jumps in financial markets:A new nonparametric test and jump dynamics[J].Review of Financial studies,2008,21(6):2535-2563.
[11]郑志勇.金融数量分析——基于Matlab编程[M].2版.北京:北京航空航天大学出版社,2013.
ZHENG Zhiyong.Financial quantitative analysis based on Matlab programming[M].2 Edition.Beijing:Beihang University Press,2013.
(责任编辑 刘 舸)
Parameter Estimation of Double Exponential Jump Diffusion Model Based on LM Method
LYU Han, CHEN Ping
(School of Science, Nanjing University of Science and Technology, Nanjing 210094, China)
This paper introduces the characteristics of the double exponential jump diffusion model, and expounds the basic idea of the Lee-Mykland method to identify the jump, and uses the maximum likelihood method to estimate the parameters, thus forming a new combination method. We use Shanghai stock index from 2010 to 2016 to do empirical analysis.The results show that using the combination method of return time series data to estimate can not only effectively estimate the parameters of the jump diffusion model, but also identify the jumping point and the corresponding parameter.
double exponential model; Lee-Mykland method; Shanghai composite index; jump recognition
2016-12-25 基金项目:国家自然科学基金资助项目(11271189)
吕韩(1991—),男,江苏泰州人,硕士研究生,主要从事金融随机分析、应用统计研究,E-mail:nplvhan@163.com。
吕韩,陈萍.基于LM方法的双指数跳扩散模型的参数估计[J].重庆理工大学学报(自然科学),2017(3):151-157.
format: LYU Han, CHEN Ping.Parameter Estimation of Double Exponential Jump Diffusion Model Based on LM Method[J].Journal of Chongqing University of Technology(Natural Science),2017(3):151-157.
10.3969/j.issn.1674-8425(z).2017.03.023
O212
A
1674-8425(2017)03-0151-07
