基于模糊综合评判的炮兵部(分)队机动训练评估
2017-04-05李伟龙黎国庆
陈 春,李伟龙,陶 晶,黎国庆
(1.陆军军官学院 二系,合肥 230031; 2. 69240部队,乌鲁木齐 830031)
【后勤保障与装备管理】
基于模糊综合评判的炮兵部(分)队机动训练评估
陈 春1,李伟龙1,陶 晶1,黎国庆2
(1.陆军军官学院 二系,合肥 230031; 2. 69240部队,乌鲁木齐 830031)
着眼炮兵部(分)队机动训练的特点,从信息获取、指挥控制、战术机动、整体防护和综合保障等方面构建炮兵机动训练的评估指标体系,采用层次分析法和模糊综合评判的方法对炮兵部(分)队机动训练进行了综合评估。
炮兵部(分)队机动;训练评估;模糊综合评判
当前,长时间、远距离机动训练是检验部队作战能力的有力举措。炮兵部(分)队机动涉及装备多,情况处置复杂,保障难度大,训练需要协调和解决的问题也复杂多样。因此,对炮兵部(分)队机动训练的评估能为部队在实战时提高机动效率和避免机动风险提供真实有效的依据和参考。
1 炮兵部(分)队机动训练评估指标及其构建
炮兵部(分)队机动训练评估一级指标通常包括信息获取、指挥控制、战术机动、整体防护和综合保障5个方面。根据部队训练的实际,综合当前部队机动训练中的主要影响因素,各个指标的二级指标如图1。
2 炮兵部(分)队机动训练评估模型的建立
2.1 层次分析法(AHP)确定各指标权重
在评估过程中,各因素的权重至关重要,它直接影响到评估的最终效果,在此引用层次分析法确定炮兵机动训练各指标的权重。同时,为了使评估更加直观,采进1~9标度方法构造比较矩阵。在求各因素的权重时,按以下步骤计算。
2.1.1 构建比较矩阵
规定奇数标度值即1、3、5、7、9按照递进的关系分别表示同等重要、略微重要、更加重要、强烈重要、绝对重要。而偶数标度2、4、6、8表示上述两个相邻判断之间的中间值。具体如表1所示。

图1 炮兵部(分)队机动训练评估指标体系

标度定义(比较因素i与j)1因素i与因素j同等重要3因素i与因素j略微重要5因素i与因素j更加重要7因素i与因素j强烈重要9因素i与因素j绝对重要2、4、6、8两相邻判断因素的中间值倒数因素i与j比较得到判断值aij,则因素j与i的判断值为aji=1/aij。
这里aij表示因素i与j重要度的比值。比值越大,说明因素i比因素j重要程度越大。例如,一级指标中a12=1/2表示炮兵部(分)队机动训练中指挥控制指标比信息获取重要性介于同等重要和略微重要之间。对于同一个元素之间的重要度应该是相同的,即aii=1。
据此,这里采用专家咨询法,选取10名资深专家给每个层次各元素进行重要性打分,对打分结果进行综合处理分别构建比较判断矩阵。
2.1.2 计算权重向量
利用判断矩阵计算各层指标对目标层的相对权重,权重通常用特征向量表示。特征向量的近似矩阵主要有求和法和求根法。本文采用求根法,即先求判断矩阵每行元素乘积的n次方根,然后进行归一化得到向量W。W即为所求矩阵。其表达式为
(1)
通过式(1)即可求得特征向量近似矩阵W=(w1,w2,…,wn),此近似矩阵即为各因素的权重。
同时,可计算出特征向量对应的最大特征值
(2)
2.1.3 判断矩阵一致性
为了避免出现逻辑上的误判,这里对矩阵进行一致性检验。一致性比例因子的计算公式为
(3)
其中C.I.的表达式为
(4)
其中:n为判断矩阵的阶数;R.I.为平均随机一致性指标,查表2可以获得。

表2 平均随机一致性指标
一般认为当一致性比例因子小于0.1时,矩阵的一致性可以接受。否则,应当对判断矩阵进行适当修改,直到满足条件为止。在得到各指标相对其上层权重的基础上,最终得到各指标对于总目标的相对权重。
2.2 二级模糊评判模型
2.2.1 建立因素集U
根据炮兵机动训练评估指标体系将因素集分成5个子集U1,U2,…,U5,满足条件
(5)
设第i个子集的因素为Ui,应满足条件
(6)
比如二级指标中信息获取因素的子因素集即为:U1={机动前的情况分析U11,机动中的情报侦察U12,机动中的情报处理U13}。
这里n=n1+n2+…+n5,n表示U的元素总个数。ni表示Ui的元素个数。
2.2.2 确定评语集V
为了更加直观地展现评估效果,在具体评估某一项指标时可以将评估结果分为若干不同的等级,所有的等级构成的集合就是评语集。考虑评估的精确性,本文将评估结果分为:优秀(V1)、良好(V2)、一般(V3)、合格(V4)、差(V5)5个等级,评语集可表示为

(7)
2.2.3 第一级综合评判
对每个因素集Ui,分别进行单因素综合评判。Ui中各因素相对Ui的权重分配为
(8)
这里应满足wi1+wi2+…+wini=1。
设Ri为Ui到V的模糊判断矩阵
rij,k表示因素Uij被评为vk隶属度。采用专家打分法确定因素Uij的隶属度。于是得出第一级模糊综合评判向量为
(9)
2.2.4 第二级综合评判向量
对因素U作二级模糊综合评判,将每个Ui视为U的一个因素,把Bi看作U的单因素模糊综合评判向量,构成U到V的模糊矩阵R
(10)
Ui为U中的一部分,反映了U的某种属性,可以按它们的重要性(层次分析法确定)给出权重分配
(11)
则第二级综合评判向量为
(12)
这里:m为评语等级,值为5;bk表示机动训练能力被评为Vk的隶属度。
按照最大隶属度原则,取B中最大隶属度对应的评判集指标作为最终评判结果。这样就确定了机动能力好坏的程度。
3 实例分析
通过咨询相关专家(10名),综合部队实际对炮兵(部)分队机动能力的各项评估指标进行评分,统计结果。这里为了便于判断,将评语集V={优秀,良好,一般,合格,差}转化成标准值h=(90,80,70,60,0)。模糊化以后的评语集的论域即为h′=(100~85,85~75,75~65,65~55,55~0)。
利用Matlab语言编写的计算程序计算得到各因素的权重和评估值。
3.1 各级因素权重计算
通过10位专家对每个因素的权重构造10个判断矩阵,计算平均权重。由于数据比较多,这里仅以第二指标层对目标层为例进行计算(见表3),其余不一一列举。

表3 第二指标层对目标层的判断矩阵(专家1)
得到专家1的权重
W(1)=(0.098 9, 0,190 7, 0.512 7, 0.098 9, 0.098 9)
n=5,故R.I.=1.12,得
C.R.=0.000 9<0.1
通过一致性检验。
其余9位专家的权重分别如表4所示。

表4 其余9位专家的权重
综合专家的打分,二级指标对目标层权重为
W=(0.105 7, 0.171 9, 0.512 1, 0.105 2, 0.105 2)
经过Matlab处理,第三层对第二层权重依次为
第三层对信息获取的权重
W1=(0.411 0, 0.289 0, 0.300 0)
第三层对指挥控制的权重
W2=(0.191 0, 0.409 1, 0.399 9)
第三层对战术机动的权重
W3=(0.444 4, 0.444 4, 0.111 2)
第三层对整体防护的权重
W4=(0.500, 0.500)
第三层对综合保障的权重
W5=(0.190 4, 0.250 3, 0.254 4, 0.304 9)
3.2 二级层次的综合评判
专家组对训练评估指标的打分情况如表5所示。
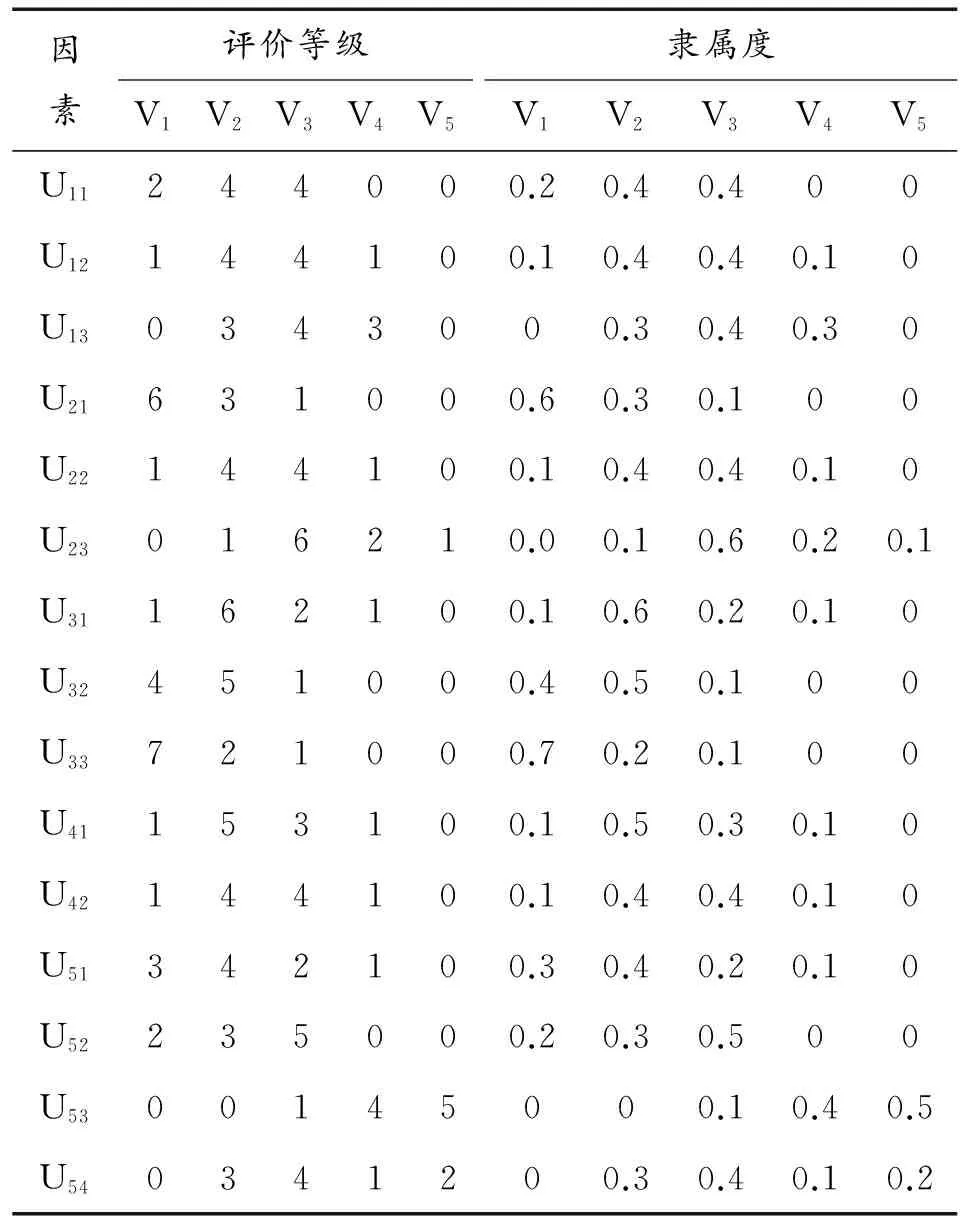
表5 专家对训练指标打分表
经过计算,得到一级指标因素的评语集为

一级指标的评估值为
H1=(74.733, 71.710, 80.660, 75.500, 59.884)
3.3 一级层次的综合评判
权重为
W=(0.105 7, 0.171 9, 0.512 1, 0.105 2, 0.105 2)
模糊判断矩阵为R,则最后评语集及评估值为
B=W·R=(0.213 9, 0.418 6, 0.258 4, 0.082 5, 0.026 7)
H=75.777
按照评语集取值范围,该部队在机动训练中,信息获取、指挥控制、战术机动、整体防护和综合保障的评估结果依次为一般、一般、良好、良好、及格。最终评估结果为良好。从结果上看,该部队基本抓住了机动训练的重点。但是该部队整体训练水平仍然有待提高。从评估的其他要素来看,基本无拔尖得分,综合保障方面相对较弱。
4 结束语
该模型避开了传统的“一锅端”的训练评估现状,引进层次分析法对不同因素按重要性进行权重设置,对部队“抓训抓重点”起到很好的引导作用。同时对各因素的评估分析也为寻找训练中的薄弱环节提供了依据。但是,模糊评判模型只能为机动训练提供一定的理论参考,要科学深入的研究实际情况,结合训练实际,灵活设置权重,确实找到部队训练的薄弱环节,提高训练水平。
[1] 司守奎,孙兆亮.数学建模算法与应用[M].北京:国防工业出版社,2015.
[2] 毕义明,刘良.军事建模与仿真[M].北京:国防工业出版社,2009.
[3] 朱奎玉.军事建模与辅助决策研究[M].北京:军事科学出版社,2014.
[4] 王莲芳,许树柏.层次分析法引论[M].北京:中国人民出版社,1990.
[5] 胡国桥,戴伟.作战指挥前沿理论研究[M].北京:国防大学出版社,2000.
[6] 陈开余,徐华.信息化炮兵作战研究[M].北京:解放军出版社,2012.
[7] 陈春.炮兵指挥自动化[M].北京:解放军出版社,2005.[8] 任富兴.炮兵信息化建设[M].北京:解放军出版社,2004.
[9] 刘洪甜,张鹏.运用模糊综合评判法对战役战术导弹所打击目标进行价值排序[J].射击学报,2004(2).
[10]张冀湘,倪发军.陆军师进攻战术演习机动处置能力评估模型[J].军事运筹与系统工程,2007,21(3):68-70.
(责任编辑 唐定国)
Artillery Maneuvering Drill Evaluation Based on Fuzzy Comprehensive Evaluation
CHEN Chun1, LI Wei-long1, TAO Jing1, LI Guo-qing2
(1.The Second Department of Army Officer Academy, Hefei 230031, China; 2.The No. 69240thTroop of PLA,Urumqi 830031, China)
Focused on the performance characteristics of artillery maneuvering drill, we built artillery maneuvering drill evaluation index system from the aspects of information acquisition, command and control, tactical maneuvering, integral protection, comprehensive support and so on. Mathematical methods such as fuzzy comprehensive evaluation, the level of analysis were used for artillery maneuvering drill assessment.
artillery maneuvering; drill evaluation; fuzzy comprehensive evaluation
2016-10-15;
2016-11-20 作者简介:陈春(1963—),男,教授,硕士,主要从事指挥信息系统研究。
10.11809/scbgxb2017.03.020
陈春,李伟龙,陶晶,等.基于模糊综合评判的炮兵部(分)队机动训练评估[J].兵器装备工程学报,2017(3):89-92.
format:CHEN Chun, LI Wei-long, TAO Jing,et al.Artillery Maneuvering Drill Evaluation Based on Fuzzy Comprehensive Evaluation[J].Journal of Ordnance Equipment Engineering,2017(3):89-92.
E271.4
A
2096-2304(2017)03-0089-04
