两岸不等高段野战管线悬挂穿越装备悬索受力分析

李 江，张伟明

(后勤工程学院，军事供油工程系， 重庆 401311)

【后勤保障与装备管理】

两岸不等高段野战管线悬挂穿越装备悬索受力分析

李 江，张伟明

(后勤工程学院，军事供油工程系， 重庆 401311)

基于悬索理论，建立了野战管线悬挂穿越装备的简易模型。根据悬索均布载荷的几何方程和力矩方程，推导出两岸不等高段野战管线悬挂穿越装备悬索受力与跨距、高差等因素的关系。通过比较等高、不等高时悬索受力，判定模型的准确性，得出相应结论，指导装备使用。

悬挂穿越；大落差；悬索；受力分析

野战管线铺设遇到河流、沟壑等障碍时常采用悬挂穿越装备实现跨越[1]。现役野战管线悬挂穿越装备基于障碍两岸等高设计，实际铺设时，两岸往往不等高，悬索形状发生变化，矢度位置改变，悬索的受力不再对称，跨越结构的受力更为复杂，若设计、安装不合理，可能造成管子接头拉脱、管线失稳等情况，影响正常输油，需对野战管线悬挂穿越装置跨越两岸不等高障碍的悬索受力情况进行分析计算。

1 模型建立

野战管线悬挂穿越装备结构和悬索受力相对简单，为便于计算，基于悬索理论将悬索线形近似的用抛物线y=ax2代替[2-3]， A、B为塔架，D为悬索最低点，悬索最低点处水平方向为x轴，垂直方向为y轴，建立坐标系，建立两岸不等高段悬挂穿越装备受力简化模型如图1所示。

图1 两岸不等高段悬挂穿越装备模型

AB间的悬索是悬链线[4-5]，如图可知此抛物线过[L-r，f]与[r，f-h]两点，将两点代入上式可得悬索曲线方程为：

(1)

式中：h为两岸高差(m);f为悬索矢度(m)；L为跨距(m)。

将点[r，f-h]代入悬索曲线方程(1)，可确定出悬索最低点D距离低测塔架B的距离r：

(2)

依据式(2)即可得出低端塔架距离悬索最低点的位置，从而确定悬索的矢度，进而进行相应的悬索受力计算。

2 受力计算

基于图1坐标系建立的简易受力模型对塔架A、B的处的悬索受力情况进行分析[6-7]。

首先对塔架B处悬索拉力进行分析，取BD段悬索上的任意点x，假设悬索在塔架B处所受的拉力为F，假设其水平方向分力为Fx，垂直方向分力为Fy。按均布荷载进行计算，忽略悬索因弯曲长度略大于x，因悬索是柔性钢索，不承受弯矩，所以∑Mx=0，由此可得：

(3)

式中：x为点x距离B点的水平距离(m)；y为点x距离B点的垂直距离(m)；q为单位长度上悬索承受的荷载(N/m)。

塔架处悬索的垂直分力就是BD段的荷载，即Fy=qr，代入式(3)：

(4)

y对x求导，得：

(5)

将x=r，y=f-h代入式(4)，整理后可求得水平拉力Fx：

(6)

将式(2)代入式(6)中得出水平拉力计算公式如下：

(7)

悬索在塔架B处的拉力FB为：

(8)

同理，假设悬索在塔架A处所受水平方向分力为Fx′，垂直方向分力为Fy′,塔架A对AD段任意点的弯矩为0，此时垂直荷载Fy′ =q(L-r),代入式(3)：

(9)

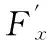
(10)

将式(2)代入式(10)：

(11)

悬索在塔架A点处的拉力FA为：

(12)

令式(7)、(8)、(11)、(12)中的h=0 m，整理后可得：

(13)

(14)

通过对比可知，本文所建模型推导出的公式在h=0 m时与两岸等高时的计算公式相同，从而证明本文建立的模型及受力计算公式推导过程正确。为进一步验证模型的准确性并比较两岸等高与不等高时的悬索拉力，找出其变化规律，使用Matlab软件计算在跨距120 m和100 m时悬索总拉力及水平拉力的变化[8-10]，结果如图2和图3所示。

图2 悬索合力变化

图3 悬索水平拉力变化

由计算结果可见，两岸存在高差时，两岸塔架处悬索的水平拉力大小相同，与两岸等高时相比均变大，且与穿越两岸的跨度、高差成正比；两侧悬索总拉力随着高差增大而增大，高海拔侧悬索总拉力比低侧塔架大。通过计算得出的悬索水平拉力及总拉力的变化趋势与实际使用过程中的悬索受力变化规律相同，变化规律符合自然规律，进一步证明建立的模型准确可靠。

由悬索受力变化规律可见，两岸不等高时，高侧塔架受力增长速率更快，易发生侧翻，倾覆等危险，需要采取必要的防护措施。

3 结论

本文基于悬索理论，应用抛物线代替悬索线，建立了两岸不等高段野战管线悬挂穿越装备的简易模型，运用该模型推导出了两岸不等高段野战管线悬挂穿越装备悬索受力计算公式，通过与等高时悬索受力公式的比较，证明推导过程正确。应用Matlab软件计算了不同高差、跨距时悬索水平受力及合力，明确了悬索受力的变化趋势，计算结果符合自然规律，证明建立的模型较为准确，可以作为现役野战管线悬挂穿越装备悬索受力计算参考，指导野战管线悬挂穿越装备的日常使用。

[1] 总后勤部军需物资油料部.野战输油管线工艺设计与铺设[M].北京:解放军出版社,2005.

[2] 李传习,刘光栋,柯红军.悬索桥主缆系统数值解析法计算的一种收敛算法[J].工程力学,2008(8):66-73.

[3] 沈锐利,王志诚.自锚式悬索桥力学特性挠度理论研究[J].公路交通科技,2008(4):94-98.

[4] 宋旭明,戴公连.自锚式悬索桥主缆线形计算方法及施工过程分析[J].中外公路,2009,29(6):135-140.

[5] 沈旺,俞建群,顾庆华,等.悬索桥主缆单元索股水平收放索技术应用智能放索装置研制[J].中国工程科学,2010(7):4-7.

[6] 檀永刚，张哲，黄才良.一种自锚式悬索桥主缆线形的解析法[J].公路交通科技，2007，24(2)：88-90.

[7] 韩艳,陈政清,罗世东.自锚式悬索桥空间主缆线形的计算方法[J].湖南大学学报(自然科学版),2007(12):20-25.

[8] 王许来,李宏伟,卢厚清.基于VV&A过程的自行舟桥训练仿真系统可信度评估指标体系[J].兵器装备工程学报，2016,37(8)：61-65.

[9] 李传习.混合梁悬索桥非线性精细计算理论及其应用[D].长沙：湖南大学，2006.

[10]黄琼，叶梅新.自锚式悬索桥简化计算方法研究[J].铁道学报，2008，30(1)：122-126.

(责任编辑 唐定国)

Stress Analysis of the Field Pipeline Suspension Equipment Using Between Large Gap

LI Jiang， ZHANG Wei-ming

(Department of Petroleum Supply Engineering, Logistic Engineering Univiersity of PLA, Chongqing 401311, China)

This paper builds the simple model of field pipeline suspension equipment based on the suspension theory. According to the geometry equation and torque equation of the suspension uniform load, the relationship of stress, height and the distance between the gap and other factors are derived. The contrast of the suspension stress of different situation shows that the model is accurate and the corresponding conclusions can guide the use of field pipeline suspension equipment。

suspension across; large gap; rope; stress analysis

2016-10-19；

2016-11-25 作者简介：李江，男，博士，讲师，主要从事油气输送技术与装备研究。

10.11809/scbgxb2017.03.019

李江，张伟明.两岸不等高段野战管线悬挂穿越装备悬索受力分析[J].兵器装备工程学报，2017(3):86-88.

format:LI Jiang， ZHANG Wei-ming.Stress Analysis of the Field Pipeline Suspension Equipment Using Between Large Gap [J].Journal of Ordnance Equipment Engineering,2017(3):86-88.

E939

A

2096-2304(2017)03-0086-03