面向装备系统评估的仿真实验因子筛选综述

杨柠檬，杨凡德，闫雪飞，施 令

(装备学院 复杂电子系统仿真实验室，北京 101416)

【装备理论与装备技术】

面向装备系统评估的仿真实验因子筛选综述

杨柠檬，杨凡德，闫雪飞，施 令

(装备学院 复杂电子系统仿真实验室，北京 101416)

在利用仿真实验评估装备系统的研究过程中，仿真实验因子筛选对于提高仿真的有效性和高效性具有重要的意义。重点针对多因子筛选技术进行了综述，介绍了实验因子筛选问题的相关概念，比较分析了几种常用因子筛选方法的步骤，归纳了现有方法的不足。现有实验因子筛选方法在应对装备系统复杂性研究方面面临挑战，仿真实验因子规模增加，因子间因果关联机理复杂，为了提高仿真实验效率和满足实验分析的整体性要求，需要探索更合理的实验因子筛选理论和方法。

复杂装备系统；仿真实验；实验因子；因子筛选方法；综述

随着信息技术的跨越式发展，武器装备系统朝着信息化、智能化和自动化等特性快速演变，开展装备系统评估是有效检验武器装备系统作战效能和建设水平的基本手段。目前比较通用的评估方法有解析法、探索性分析方法、作战试验和仿真实验等手段，其中仿真实验方法是目前最重要的研究途径。采用仿真方法评估复杂装备系统，通常首先选取相应的评估指标作为输出，然后选取与评估指标相关的实验因子作为输入，通过分析仿真实验结果，获取评估指标结论。

仿真实验因子筛选的合理性事关仿真结论的可靠性，目前在生物医学、供应链等应用领域已经开展了部分因子筛选方法研究工作，但是针对复杂装备系统或者装备体系作战效能评估的仿真实验因子筛选研究工作还较为稀缺，本文面向复杂装备系统效能评估的需求背景，对仿真实验因子筛选方法进行综述，对于相关研究具有一定的参考价值。

1 因子筛选相关概念

根据Pareto定理或20-80法则[1]，认为在仿真实验中，只有少部分的实验因子能起到关键的主导作用，所以实验人员只需要选取重要的实验因子进行仿真实验。实验因子筛选方法的发展从方法适用的因子数来说，是从适用因子数少到适用因子数多的一个发展。目前对于实验因子筛选方法，大致可以分为两类：一是针对少量实验因子；二是针对大量实验因子。

1) 针对少量实验因子

开始是20世纪30年代Fisher在农业数据统计和分析中，根据随机化、重复、区组化的基本原则提出了析因设计的概念，从是否把全部因子组合都考虑的角度出发，具体可以分为全面析因设计和部分析因设计，析因设计也成为上个世纪的主流方法。其中，常见的部分析因设计有正交设计、均匀设计、分式析因设计等。在分式析因设计中，2k析因设计是应用最为广泛的一种方法。1951年，Box和Wilson在前人基础上提出了响应曲面法[2](Response Surface Methodology,RSM)，充分考虑工业试验中序贯性和及时性的特点，在拟合的输入输出模型中，能确定输出达到最优的因子组合。日本田口玄一博士提出田口法，与传统优化方法相比，可以在充分考虑全局、整体的基础上得到自身参数以及与其他参数共同作用对输出的影响[3]。20世纪70年代，出现了蒙特卡洛抽样和拉丁超立方分层抽样的方法，应用最多的是由Mckay等人提出的拉丁超立方抽样[4](Latin Hypercube Sampling,LHS)。1978年，由于在导弹设计时的需求，我国方开泰与王元提出了均匀设计[5]的方法，适用于因子数和水平数较多但需要较少实验次数的情况。

2) 针对大量实验因子

对于大量实验因子的筛选方法，应用最广的是顺序分支法[6](Sequential Bifurcation，SB)，开始是1996年由Bettonvil and Kleijnen提出的，这是一种非常有效，也是效率较高的方法。2003年，Hong Wan对这种方法进行改进，提出CSB法[7](Controlled sequential bifurcation)，这种方法能控制第一类错误和重要因子被筛选的概率，后来又充分考虑到因子间交互作用提出CSB-X方法[8]，X代表交互作用。2005年，Sanchez 和Hong Wan提出两阶段筛选方法[9](Two-Phase Screening Procedure for Simulation Experiments)，在第一阶段采用分式析因设计；第二阶段采用CSB或CSB-X方法。Hua Shen和Hong Wan于2008年提出CSFD(Controlled sequential factorial design)方法[10]，将序贯性假设检验和分式析因设计相结合。Hua Shen和Hong Wan在2010年提出二阶段分组筛选法[11](Two-Stage Group Screening)。2013年施文提出SB-RSM方法[12]，首先运用顺序分支法进行因子筛选，筛选出重要因子，对运用响应面法寻找重要因子的最高水平。2014年施文和Kleijnen 提出多响应的顺序分支法[13](Multi-response SB,MSB)，运用顺序分支法在随机仿真实验中获得更多的响应。

一般情况下，实验因子筛选方法的选择是根据仿真实验中因子数量决定的，对于较少的因子数(少于等于5)，采用2k析因设计；在少于20个因子数的情况下，选用分式析因设计(2k-p)是最好的；对于成百上千的实验因子数，采用迭代分式析因设计(Iterated Fractional factorial Design，IFFD)；对于几十上百的因子数量，采用二阶段分组筛选和顺序分支法是最好的[14]，所以本文主要介绍以上几种方法。

1.1 一般概念

首先介绍一下实验因子筛选中非常重要的概念[15]。在仿真实验中，一般将筛选[16]定义为：“在大量实验因子中寻找最重要的因子”。筛选的目的就是从一系列潜在的、有可能性的重要因子中选出真正的重要因子，这些选择的重要因子必须经过合适的方法进行最佳、有效地分析。实验因子被定义为可控的输入变量，其变化可以影响输出的变化。实验因子筛选方法的评价准则[17]应该考虑：

1) 效率。效率是通过仿真实验进行的试验次数来考量的，进行筛选的运行试验次数越少，效率越高。

2) 有效性。有效性的考核标准就是能不能保证重要因子都被筛选出来，筛选出来的都是重要因子。

3) 稳健性。稳健性是应用实验因子筛选方法时有没有考虑实验因子的先验知识，有没有运用假设条件。

4) 简捷性。简捷性是就是应用筛选方法的容易程度，较之前面3个准则，在适当情况下简捷性可以不加考虑。

1.2 主效应和交互效应

1) 主效应

因子主效应指的是通过改变因子的输入使输出有一个最大的变化值。若因子对输出的影响是单调的，那么因子的高、低水平值和所对应的输出值的差的绝对值，即为因子对输出影响的主效应大小。

2) 交互作用

因子间的交互作用[18](Interaction between the factors)：一个因子对实验指标的影响会根据另一因子水平的变化而产生不同的变化，此时称这两个因子间有交互作用。例如因子A与B有交互作用，记为A*B或AB。

3) 主效应方向

主效应方向是用来衡量因子对输出的正负影响，是指随着实验因子输入水平的逐渐增大，输出值是增大还是减小，增大用正号表示，减小则用负号表示。显然，若因子对输出的影响是单调增的，那么主效应的方向为正；若因子对输出的影响是单调减的，那么主效应的方向为负。

分辨率[19]在分式析因设计有相当重要的作用，其中分辨率为III、IV、V的情况非常重要，具体定义如下：

1) 分辨率为III：其中因子之间主效应没有混淆，因子主效应可以与其他因子二阶交互作用互为别名；

2) 分辨率为IV：其中因子主效应与其他因子主效应以及因子二阶交互作用没有混淆，但因子二阶交互作用可以互为别名；

3) 分辨率为V：其中因子主效应或因子二阶交互作用与其他因子中因子主效应或因子二阶交互作用没有混淆，但因子二阶交互作用可以与三因子交互作用互为别名。

2 筛选方法

2.1 析因设计方法

20世纪二三十年代Fisher基于农业数据统计提出了析因设计的概念，析因设计又可以分为完全析因设计和部分析因设计[20]。析因设计是应用比较多的一种实验因子筛选方法，针对于因子数量少的情况下，析因设计是非常有效的方法。

2k析因设计是特殊的一类析因设计，其中因子个数为k个，且每个因子的取值只有两个水平，因此所需要的试验次数即为2k次，适用于因子数较少的情况下。当因子数相对多一点的情况下，2k析因设计就会出现非常大的计算量，为了提高实验效率就提出了2k-p分式析因设计，其中k为总因子数，k-p为实验所需的因子数，因此试验次数即为2k-p次，其主要步骤为[21]：

1) 确定实验因子数目、水平以及分辨率，把每个因子都设定为两个水平值，即高水平和低水平；

2) 将选择的k-p个实验因子按照高水平取+1，低水平取-1设计全因子实验矩阵；

3) 实验矩阵设计完成后，根据全因子设计中的计算和分析方法，分别计算其因子主效应和因子间的交互作用。

2k析因设计和2k-p分式析因设计主要是针对实验因子数很少的情况，优点是不需要考虑因子单调性和主效应，最主要的缺点就是不能处理因子数多的情况，因子数一旦增多，就会导致实验次数成指数级增长。

2.2 迭代分式析因设计方法

迭代分式析因设计[22](Iterated Fractional factorial Design，IFFD)最初是由Andres and Hajas提出的，应用于超大数量的实验因子筛选，目的是从成百上千的因子中找出少数重要因子。其主要步骤为：

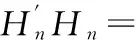
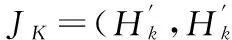
第一步，将因子随机对应JK矩阵中所在列，如果因子数N大于列数K，则多出的因子就会和其他部分因子有共同的所在列，就会因为叠加导致无法分辨因子间交互作用，因此需要保证列数K大于N。

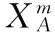
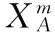
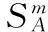
就处理因子数来说，迭代分式析因设计能处理的因子数是最多的，且具有不需要考虑因子单调性和主效应的优点，实验次数可以接受，但由于处理因子数量大，构建矩阵相对复杂，导致计算难度比较大。

2.3 顺序分支法

目前群组筛选是应用比较多的方法，其中最主要的就是以顺序分支法(SB)以及改进方法为代表的一系列实验因子筛选方法[24]。SB法开始将所有因子归到同一个组当中，然后判定这个组当中是否有重要因子，如果有，就继续将因子分成两个组，分别判断是否有重要因子，如果没有就舍弃，如果有就继续分组判断，最后将不重要因子剔出，筛选出重要因子。例如，对16个因子进行筛选，如图1所示。

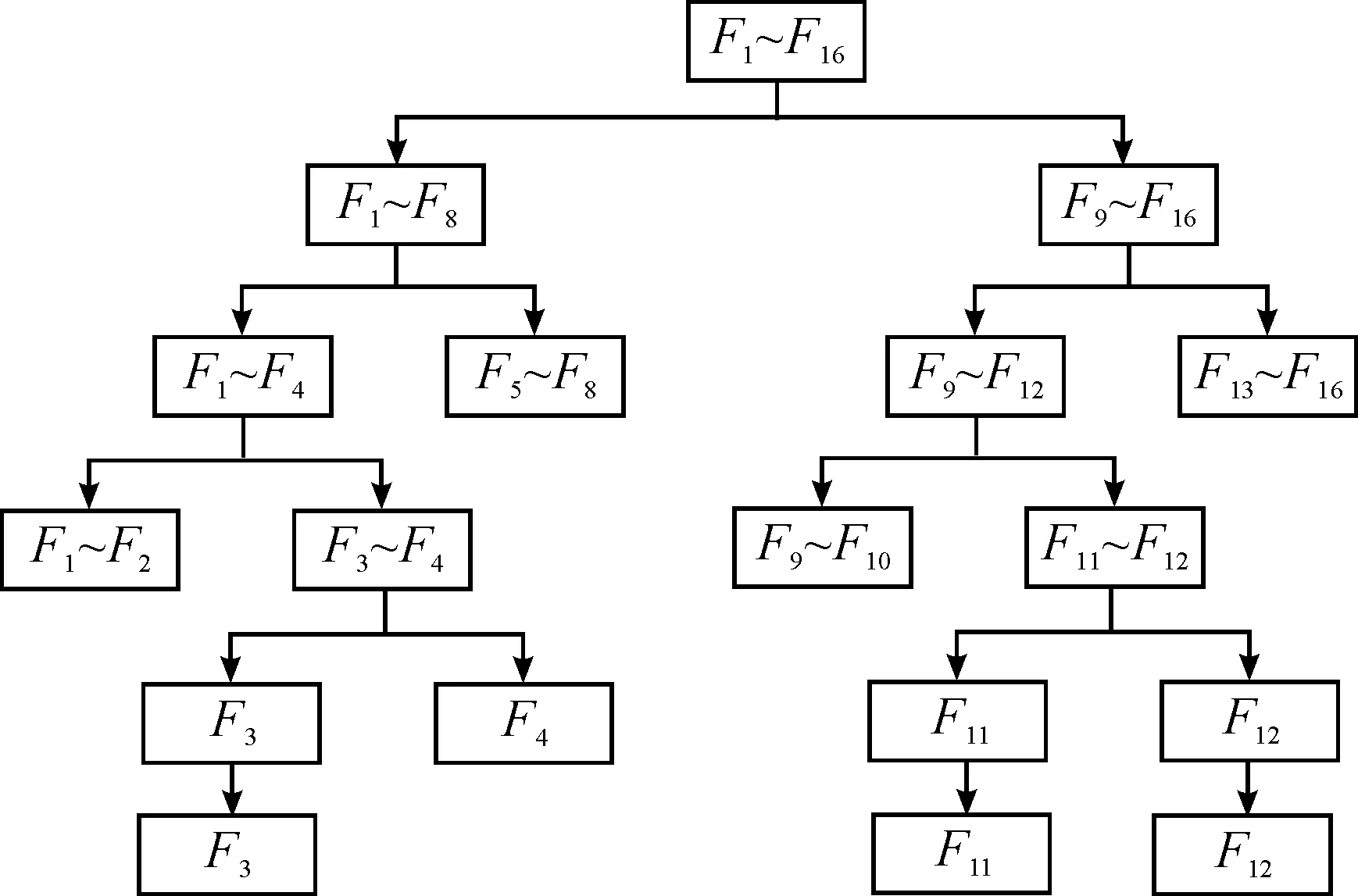
图1 筛选示例

基于SB法，有两个假设条件[25]：

1) 仿真实验的输入输出近似由一阶元模型表示：

式中Y表示输出，xj表示j的值，在[-1,1]之间取值，高水平时取值1，低水平时取值-1，βj代表第j各因子的主效应大小，其中e表示误差。

2) 每个实验因子只要存在主效应，那么因子的主效应符号就可确定。

现在定义下面的符号并给出意义：

Y(j);r：表示第r次仿真实验时的输出，其中,xj从x1到xj取+1，k以后取值-1，β从β0到βj取高水平，βj以后取低水平；

βi-j：表示从i到j各因子的主效应之和；

第r次实验中βi-j的总体估计值为：

单个因子在第r次实验中的主效应为：

注意这些等式都是在没有考虑因子间交互作用时成立，平均总体和平均单个因子主效应计算如下：

运用顺序分支法时需假设前提，即需要知道因子单调性和因子主效应方向。顺序分支法处理的因子数相对较多，实验次数也相对较少，但顺序分支法在因子间交互作用上考虑不够，且在因子分组上进行的实验次数也只有一次。

2.4 二阶段分组筛选法

二阶段分组筛选法(Two-Stage Group Screening)主要是先根据先验知识将因子分为逻辑组并进行分式析因实验[26]，然后判断该组因子中是否含有重要因子，若该组不含有重要因子，则舍弃；如果有，则继续拆分直到找出重要因子。与顺序分支法相比二阶段分组筛选法主要有两个方面不同：

1) 在将因子分为逻辑组方面

一般情况下，顺序分支法会直接将因子进行排序分组，而二阶段分组筛选法将因子分为逻辑组[27]，在一定程度上考虑了相互影响的因子；顺序分支法对因子进行分组会采取均匀分组或是第一个因子组是2的倍数，而二阶段分组筛选法在一个逻辑组中选择的因子数可以根据具体情况改变。

2) 采用分式析因方面

顺序分支法的一般元模型没有考虑因子间交互作用，只对分组进行一次实验，因此忽略了因子之间的相互影响。二阶段分组筛选法利用分式析因对每个逻辑组都进行实验，能够考虑到因子间的交互作用，而且在分组过程中会将相互影响较大的因子划分到同一个组中，这样能保证较好地分析因子间的相互作用。

运用二阶段分组筛选之前需要知道因子单调性和因子主效应方向，二阶段分组筛选在实际情况下不仅考虑到因子间交互作用，而且对因子分组都进行实验，相对更加完善。

3 结论

本文比较分析了几种常用因子筛选方法，从实验次数、单调性要求、处理因子数和主效应方向需求的角度出发进行对比。其中，实验次数代表效率，单调性要求和处理因子数代表稳健性，主效应方向需求代表方法应用的前提假设，具体如表1所示。

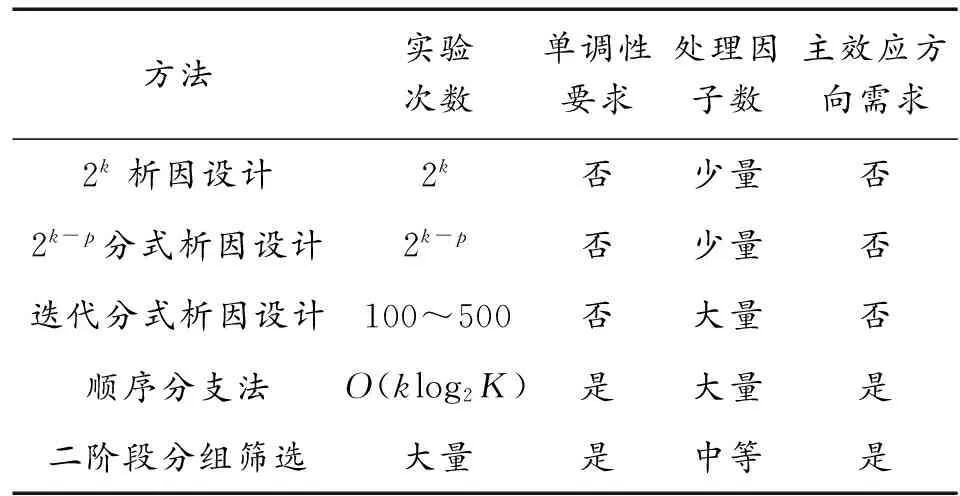
表1 不同因子筛选方法对比

由表1比较可知，处理的因子数不同，各方法所需实验次数不同，效率也就不同。处理因子数由多到少依次是迭代分式析因设计，顺序分支法，二阶段分组筛选，2k-p分式析因设计和2k析因设计。从是否需要单调性和主效应方向分析，2k析因设计，2k-p分式析因设计和迭代分式析因设计不需要这两个假设前提，而顺序分支法和二阶段分组筛选由于模型原因需要假设前提。

本文分析比较了几种常用的因子筛选方法，根据这些方法的适用特点，在对复杂装备系统开展仿真实验评估时，需要针对具体仿真对象，采用具体方法分析和设计仿真实验因子。一般情况下，根据复杂装备系统进行仿真实验过程中，从准备选取实验因子的个数、所需要的实验次数、人力物力和时间成本等角度综合考虑，选用合适的实验因子筛选方法进行研究，不应局限于其中一种方法。对于这些方法，其缺点和需要的假设条件有待进一步完善；从另一个角度来说，还迫切需要具有普遍适用性的、假设条件少的新的筛选方法。针对复杂装备系统或者装备体系作战效能评估的仿真实验因子筛选研究工作还需进一步深入，适合于复杂装备系统的因子筛选方法还需进行探索。

[1] SIMPSON T W,BOOKER A J,GHOSH D,et al.Approximation methods in multidisciplinary analysis and optimization:a panel discussion[J].Structural and Multidisciplinary Optimization，2004，27(5)：302-313.

[2] GUO Li,CAI Xiaolan,ZHOU Lei,et al.Optimization of Process Parameters for in High-Energy Ball Milling of CNTs/Al2024 Composites Through Response Surface Methodology[J].Journal of Harbin Institute of Technology,2016(1):1.

[3] BHOTE K B,陈忠琏.实验设计(DOE):通向质量的高速公路[J].数理统计与管理,1990(6):45-52.

[4] CHOI S K,GRANDHI R V,CANFIELD R A,et al.Polynomial Chaos Expansion with Latin Hypercube Sampling for Estimating Response Variability[J].Aiaa Journal,2015,42(6):1191-1198.

[5] 汪树清.均匀设计及其应用[M].北京：中国医药科技出版社,2005.

[6] KLEIJNEN J P C.Regression and Kriging Metamodels with Their Experimental Designs in Simulation: Review[J].Discussion Paper,2015,35(1):1-16.

[7] WAN H,ANKENMAN B E,NELSON B L.Improving the Efficiency and Efficacy of Controlled Sequential Bifurcation for Simulation Factor Screening[J].Informs Journal on Computing,2010,22(3):482-492.

[8] HONG W,ANKENMAN B E,NELSON B L.Simulation Factor Screening With Controlled Sequential Bifurcation in the Presence of Interactions[J].2006.

[9] SANCHEZ S M,WAN H,LUCAS T W.Two-phase screening procedure for simulation experiments[J].Acm Transactions on Modeling & Computer Simulation,2009,19(2):223-230.

[10]SHEN H,WAN H.Controlled sequential factorial design for simulation factor screening[C]//Conference on Winter Simulation.Winter Simulation Conference,2009:511-519.

[11]PATEL M S,OTTIENO J A M.Two-stage group-screening designs with equal prior probabilities and no errors in decisions[J].Communications in Statistics-Theory and Methods,2010,13(9):1147-1159.

[12]施文,刘志学,刘丹.零部件循环取货越库物流系统关键因子研究——仿真实验设计与分析方法[J].管理科学学报,2013,16(6):22-34.

[13]SHI W,KLEIJNEN J P C,LIU Z.Factor screening for simulation with multiple responses:Sequential bifurcation[J].European Journal of Operational Research,2014,237(1):136-147.

[14]TROCINE L,MALONE L C.Finding important independent variables through screening designs:a comparison of methods[C]//Simulation Conference Proceedings.IEEE Xplore,2000:749-754.

[15]胡剑文.作战仿真实验设计与分析[M].北京：国防工业出版社,2010.

[16]MARTIN R A G,SANCHEZ J M G.Screening for important factors in large-scale simulation models:some industrial experiments[J].2015.

[17]TROCINE L,MALONE L C.An overview of newer,advanced screening methods for the initial phase in an experimental design[C]//Simulation Conference,2001.Proceedings of the Winter.[S.l.]:[s.n.],2001:169-178.

[18]WANG X D,TIAN J.The Estimation for Interaction Between the Factors and the Confidence Intervals in Multivariate Analysis[J].Mathematics in Practice & Theory,2009,39(10):122-126.

[19]LEE S H,HAN S,PEA-MORA F.Hybrid System Dynamics and Discrete Event Simulation for Construction Management[C]//International Workshop on Computing in Civil Engineering.[S.l.]:[s.n.],2014:232-239.

[20]王青松.仿真实验因子筛选方法及工具研究[D].哈尔滨：哈尔滨工业大学,2015.

[21]万秋生.复杂仿真实验设计与监控技术研究[D].哈尔滨：哈尔滨工业大学,2012.

[22]WOODS D C,LEWIS S M.Design of Experiments for Screening[M].Springer International Publishing,2015.

[23]KHARE Y P,MUOZ-CARPENA R,ROONEY R W,et al.A multi-criteria trajectory-based parameter sampling strategy for the screening method of elementary effects[J].Environmental Modelling & Software,2015,64(C):230-239.

[24]SHI W,SHANG J,LIU Z,et al.Optimal design of the auto parts supply chain for JIT operations:Sequential bifurcation factor screening and multi-response surface methodology[J].European Journal of Operational Research,2014,236(2):664-676.

[25]RAGHEB M,REKAB K,TADJ,et al.Screening alexandria port simulation model by using sequential bifurcation procedure[J].International Journal of Simulation Modelling,2010,9(2):98-109.

[26]NOWAK A S.Two Stage Group-Screening Designs with Unequal A-Prior Probability.Communications in statistics.Theory and methods[C]//Recent Advances in Engineering Mechanics and Their Impact on Civil Engineering Practice.ASCE,2015.

[27]MALLON J C,ANDERSON J S.Correction:A Critical Assessment of Two-Stage Group Screening through Industrial Experimentation[J].Plos One,2014,9(2):e98605.

(责任编辑 周江川)

Review on Factor Screening Methods of Simulation Experiments for Evaluating Equipment System

YANG Ning-meng, YANG Fan-de, YAN Xue-fei, SHI Ling

(Science and Technology on Complex Electronic System Simulation Laboratory, Academy of Equipment, Beijing 101416, China)

Factor screening of simulation experiment is very important for improving the effectiveness and efficiency of the simulation in the process of evaluating equipment system by simulation experiment. The multi factor screening technology is reviewed. Firstly, we introduced the related concepts of experimental factor selection problem, and then analyzed some factor selection steps, and finally we summarized the deficiencies of the existing methods. In our opinion, the existing experimental factor screening methods are facing challenges in the aspects of coping with the complexity of equipment system like the increasing scale of factor and the causal relationship between the complex mechanism factor, and in order to improve the efficiency and meet the overall requirements of experiment, more reasonable screening theories and methods are needed to explore.

complex equipment system; simulation experiment; experiment factor; factor screening method; review

2016-10-25；

2016-11-30 作者简介：杨柠檬(1993—)，男，硕士研究生，主要从事装备系统论证与仿真评估研究。

杨凡德(1971—)，男，硕士，研究员，主要从事信息系统分析与集成研究。

10.11809/scbgxb2017.03.015

杨柠檬，杨凡德，闫雪飞，等.面向装备系统评估的仿真实验因子筛选综述[J].兵器装备工程学报，2017(3):67-71.

format:YANG Ning-meng, YANG Fan-de, YAN Xue-fei, et al.Review on Factor Screening Methods of Simulation Experiments for Evaluating Equipment System[J].Journal of Ordnance Equipment Engineering,2017(3):67-71.

E257

A

2096-2304(2017)03-0067-05