基于固定弹道的空间拦截发射点快速选择研究

魏鹏涛，韩宝珠，廖永刚

(火箭军指挥学院，武汉 430012)

【装备理论与装备技术】

基于固定弹道的空间拦截发射点快速选择研究

魏鹏涛，韩宝珠，廖永刚

(火箭军指挥学院，武汉 430012)

针对地基导弹对空间目标拦截需要选择合适发射点，对于弹道固定的空间目标，对拦截点进行了规划，建立了拦截弹主动段弹道模型和自由段弹道模型，给出了发射点选择模型，采用牛顿迭代算法对所建立的非线性方程组进行了解算。结果表明，所选择发射点能满足空间拦截要求。

空间拦截；固定弹道；发射点选择

随着航天科技的发展，空间的作用日益凸显，空间飞行器逐渐增多，在许多方面都发挥着重要的作用，但是随之而来出现其他一些问题，如：部分飞行器达到工作年限会报废，部分飞行器技术性能无法适应新的需求，需要对其进行更换，因此，对这些飞行器的快速处理便显得尤为重要。对这些空间飞行器的快速处理，通过使用地基导弹等武器直接进行拦截是一种有效的处理方式。地基导弹空间快速拦截有许多方法，比如重新设计弹道、空间机动变轨等，部分文献进行了相关研究[1-4]。针对固有弹道，通过选择发射点实现对目标的拦截是一种最快捷、最有效的方法，但是目前可以见到的研究文献相对较少。本文拟在固定弹道的基础上，通过选择合适的发射点，实现在预定拦截点对目标的拦截。本文方法可为空间快速拦截提供技术参考。

1 拦截点规划和弹道模型

1.1 拦截点规划

选择合适的拦截点是需要研究的一个重要课题。对不同的空间飞行器轨道，拦截点的选取也不同。拦截点的选择要考虑以下几方面因素：① 在拦截点区域的轨道测量精度应该比较高；② 拦截效率应该较高；③ 交会角和能量的影响，交会角越大，拦截概率越小，同时拦截点选择应该使导弹拦截所消耗的能量最小[5]；④ 拦截点选取的约束条件。目标飞行器与拦截弹的碰撞是硬杀伤，如果该碰撞发生在其他主权国空域，尤其是俄罗斯、日本等空域，将可能因国家安全性引起不必要的国际纠纷，应将拦截点选在公海或我国空域。

1.2 弹道模型

1.2.1 主动段弹道模型

用一种两级推进的导弹为研究对象。建立发射坐标系下拦截弹的运动方程，主要包括：质心运动方程、姿态控制方程、联系方程、瞬时平衡方程、发动机推力和推进剂秒流量计算式及关机方程等[6]。它们较精确地描述了拦截弹在主动段的运动规律。由于方程比较复杂，这里不一一列出，参见文献[6]。

1.2.2 自由段弹道模型

在自由段，导弹一般只受地球引力作用，如果把地球视为匀质圆球体(即地球引力场为有心力场)，那么导弹将按照椭圆弹道规律飞行。

为了使描述导弹运动的微分方程获得解析解，方便控制系统分析和导弹初步设计，导弹的自由段运动应基于下列假设：① 导弹的自由段运动是在真空进行的；② 导弹仅受地球引力的影响；③ 不考虑地球的自转及绕太阳的公转；④ 地球为质量分布均匀的圆球体。

在椭圆弹道假设条件下，导弹自由段飞行弹道方程为

(1)

其中

(2)

式中：h为导弹任一瞬时对地心动量矩；μ=fM为地球引力常数；c为初始极轴；e为偏心率；f为极角。

2 发射点选择

2.1 模型建立

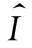
发射坐标系[g]和地心赤道坐标系[s′]的转换关系为

(3)

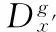
(4)

式(4)中，各矩阵元素为

(5)

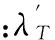
发射点在地心赤道坐标系下的坐标可表示为[7]

其中：BT为发射点天文纬度；λT为天文经度；H为发射点高程；Re为地球赤道半径；f=0.003 353;θ为发射点恒星时。

假设导弹发射t时间后拦截目标，此时拦截弹发射系坐标[xt]=[xt,y,zt]T，则由式(3)得拦截弹拦截时刻在地心赤道坐标系下的坐标为

因此，可以得到非线性方程组

F=xm-xs=0

其中xm=[xm,ym,zm]T为目标飞行器拦截时刻在地心赤道坐标系下的坐标。

2.2 算法设计

本文选用牛顿迭代算法。牛顿迭代算法是求解非线性方程组的最基本而且十分重要的方法，目前使用的很多有效的迭代法都是以牛顿迭代算法为基础，并由它发展而得到的。它具有超线性收敛性和自校正等优点[8]。算法流程图如图1所示。

3 仿真分析

空间目标轨道如表1所示。假定拦截时刻为2015年6月1日19∶46∶40。选择两级火箭动力拦截弹参数，假设2级关机时间为245 s。假定被动段飞行时间179 s。那么拦截弹发射时刻应为2015年6月1日19：39：36。因而发射时刻格林尼治恒星时θG=185.498°。

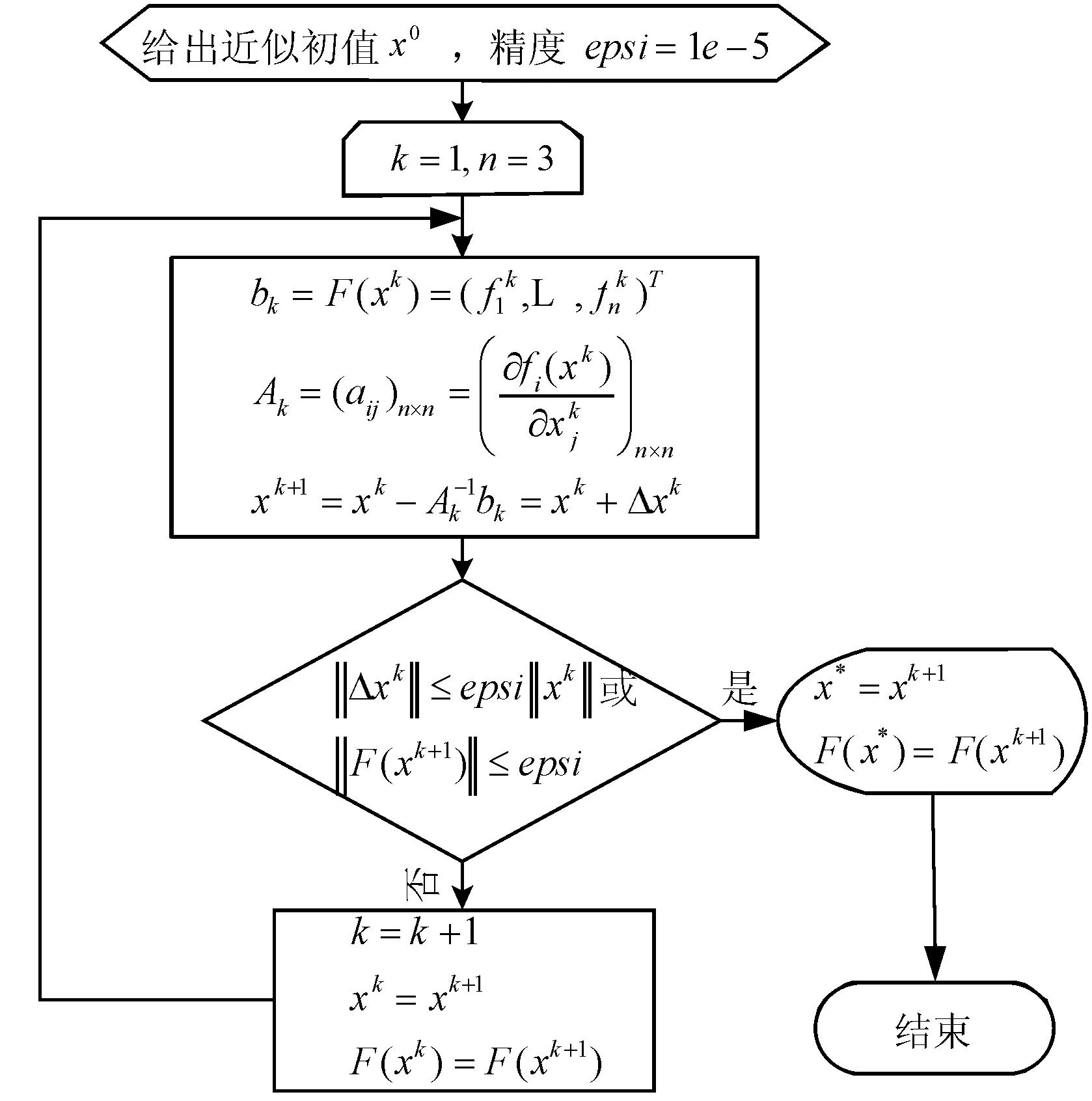
图1 算法流程

长半轴/km偏心率轨道倾角/(°)升交点赤经/(°)近地点幅角/(°)7017.19070.045797.8000-60.000090.0000

设定初值为BT0=40°，λT0=110°，AT0=150°。导弹飞行424 s后导弹在发射坐标系下的速度坐标为(5 975.7，-0.5，303.7)(单位：m/s)，位置坐标为(1 652 887.2，316 397.0，61 268.3)(单位：m)。将此坐标转换到地心赤道坐标系，用牛顿迭代算法求解非线性方程组，得到优化解：BT1=32.284°，λT1=104.357°，AT1=147.975°。因此，发射点位置地心赤道坐标为(2 418.390，-4 713.568，3 540.321)(单位：km/s)。所做仿真计算在CPU为920/2.67GHz，4G内存的台式机上完成，采用Matlab语言编程，所需时间：1.179 s。

拦截仿真如图2所示。由图2可以看出优化的导弹拦截轨道面和目标轨道面之间的夹角很小，满足拦截所需的能量要求，因此该发射点是可行的。同时该方法满足快速性要求。

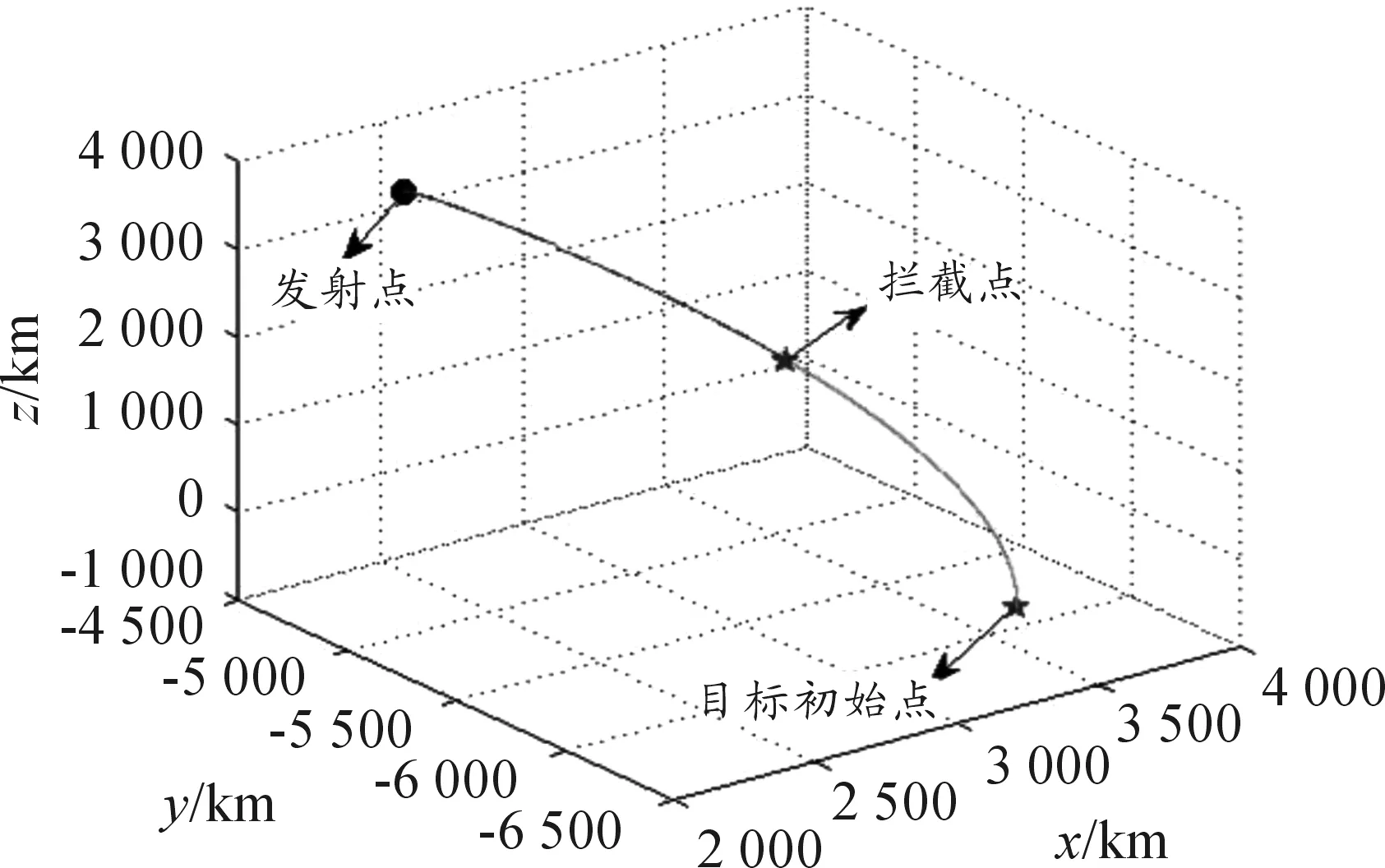
图2 导弹拦截空间目标仿真

4 结束语

为了快速完成某次拦截任务，对于固定弹道的导弹来说，寻找合适的发射点是需要解决的一个重要课题。本文以两级火箭动力拦截导弹为研究对象，针对其弹道固定的情况，采用牛顿迭代算法搜索发射点，可实现对空间目标的快速拦截。下一步，将对其实际可行性展开研究，为空间快速拦截提供技术参考和借鉴。

[1] 张鹏宇.空间拦截最优轨道设计[D].哈尔滨：哈尔滨工业大学，2009.

[2] 陈茂良，周军，常燕.空间拦截攻击区和威胁区仿真研究[J].航天控制，2009，27(1)：41-44.

[3] 张柏楠.航天器交会对接任务分析与设计[M].北京：科学出版社，2011.

[4] 袁建平，和兴锁.航天器轨道机动动力学[M].北京：中国宇航出版社，2010.

[5] 王继平，鲜勇，王明海，等.轨道交角与时间偏差对拦截卫星拦截概率的影响[J].飞行力学,2008，26(5)：89-92.

[6] 张毅，肖龙旭，王顺宏.弹道导弹弹道学[M].北京：国防科技大学出版社，2007.

[7] HOWARD D，CURTIS.轨道力学[M].周建华，徐波，冯全胜，译.北京：科学出版社，2009.

[8] 邓建中，刘之行.计算方法[M].西安：西安交通大学出版社，2001.

(责任编辑 周江川)

Study on Quickly Choosing Launch Point of Space Interception Based on Fixed Trajectory

WEI Peng-tao, HAN Bao-zhu, LIAO Yong-gang

(The Rocket Force Command College, Wuhan 430012, China)

Aiming to that ground missile interception of space target needs to choose suitable launch, for missile of fixed trajectory, intercept point was selected to satisfy interception condition. Mathematical models of calculating the powered trajectory and the free-flight trajectory were established. The selected mode of launch point was put forward. Newton method was adopted to calculate the non-linear equations. The results show that the selected launch point can satisfy the space interception demand.

space interception; fixed trajectory; selecting launch point

2016-10-21；

2016-11-25 作者简介：魏鹏涛(1983—)，男，博士，讲师，主要从事飞行动力学与制导理论研究。

10.11809/scbgxb2017.03.008

魏鹏涛，韩宝珠，廖永刚.基于固定弹道的空间拦截发射点快速选择研究[J].兵器装备工程学报，2017(3):35-37.

format:WEI Peng-tao, HAN Bao-zhu, LIAO Yong-gang.Study on Quickly Choosing Launch Point of Space Interception Based on Fixed Trajectory[J].Journal of Ordnance Equipment Engineering,2017(3):35-37.

V525

A

2096-2304(2017)03-0035-03