现代宜居城市排名评价方法
2017-04-04刘永坤宋朝炀鲍雅兰
刘永坤 宋朝炀 鲍雅兰
本文围绕城市宜居性的评价问题进行研究, 构建评价指标体系,建立了基于MIV神经网络变量筛选模型、AHP层次分析法评价模型、sobol全局灵敏度分析法模型,评价各类因素对城市宜居性的影响,通过Matlat和SPSS求解出各个城市宜居性评价值。
一、问题的叙述
宜居性城市评价指标体系不同,宜居城市排名结果也会发生变化。一座宜居的城市不仅应具备物质丰足、生活便利等条件,而且应注重人们的切身感受。人们选择留在某个城市,不单是为了生存,更是寄托了自己的梦想与希望。对很多人来说,衡量是否宜居或许就是八个字:衣、食、住、行、安、居、乐、业。
问题1:通过查阅资料,筛选评价宜居城市的主要指标,并阐述这些指标的合理性。根据所筛选的主要指标,建立评价宜居城市的数学模型。
问题2:构建的评价宜居城市的数学模型,对淮海经济区内的8个城市(宿迁、连云港、宿州、商丘、济宁、枣庄、徐州、淮北)进行合理性研究,给出宜居城市排名。
二、模型的建立与求解
1.问题1模型的建立与求解
(1)问题1模型的准备
①评价宜居城市指标的选取
为了建造一个合理而且实用性广的评估宜居性城市模型,我们要对所有评估宜居性城市的指标做一个综合性的概括。指标如图1所示:
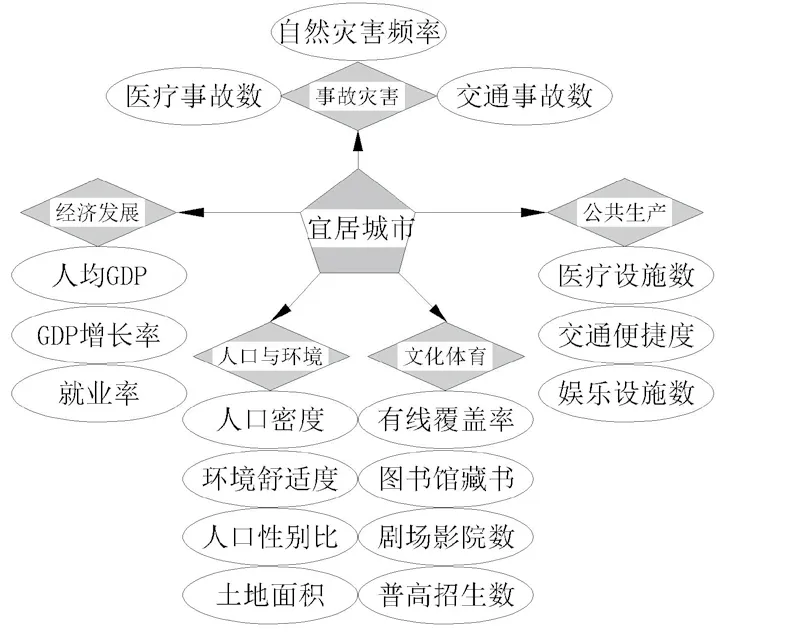
图1 评价宜居城市的指标图
②指标选取的合理性解释
衡量是否宜居的八个字:衣食住行、安居乐业,表明医疗、娱乐等基础设施也是其评价指标。经济繁荣与就业又密不可分,人均GDP等也就成为评价宜居性城市的重要指标之一。追求繁荣需要发挥城市聚集效应,追求舒适需要城市分散,为了城市有效经营必须遵守城市经济学原理——分散与聚集人口密度,土地面积自然而然也成了评价指标。
(2)问题1模型的建立
①基于MIV神经网络变量筛选对指标预处理模型的建立

对影响城市宜居程度高低的7个关键指标是根据MIV值的绝对值排名决定的,结合实际情况,这些指标确实对城市宜居程度高低的评定有重要决定作用。
②AHP层次分析法确定权重模型的建立
Step two建立层次结构。将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为中间层和最底层。这里的准则层是二级指标中的各类因素,目标层是城市宜居程度的评估值。
Step three两两比较7个指标的重要程度,根据satty 7级标度方法我们可以得到一致性。其中,我们将影响评价对象的指标作为一致性矩阵的行与列标题矩阵的每个元素,可以代表两两因素相比的重要程度。将矩阵的行标题比上列标题,重要程度如下表1,构造判断矩阵。

表1 两两因素对照表
根据建立的判断矩阵,使用Matlat程序进行计算各项权重
为了确认权重的合理性,我们进行了一致性检验。
计算层次单排序并作一致性检验。对比较矩阵计算最大特征值及其对应的特征向量,利用一致性指标
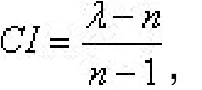
和一致性比率

Step four为了给出城市宜居程度的评估值,我们需要找一个评价标准。此处我们选定平均值为我们的评定指标。因为我们研究的是整个地区各个城市的宜居水平,既然这样,我们便可以将整个地区的平均水平作为评定指标的最中等水平。以此平均水平向正负两个方向等距延伸形成相应的评价等级,即高于平均水平为高或极高,低于平均水平为低或极低。
以医疗设施数量为例,首选我们查出给定的整个地区医疗设施的总数,计算出其对总人数的平均值。然后相应的根据每个城市的医疗设施总数为以及对应的人口总数,计算出其平均值,由此可用
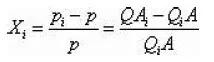
作为第i个城市医疗设施对其宜居程度的影响。同样的如果是成本型指标M,则可用
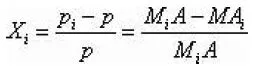
作为第i个城市的成本型指标对其宜居程度的影响。
Step five将各个指标的等级值乘上对应的权值,可得到某城市宜居程度值,数越大,就说明该城市宜居程度越高。
2.问题2模型的建立与求解
(1)基于MIV神经网络变量筛选模型对指标的降维
通过查找影响城市宜居能力的指标,由于指标过多,计算时间耗费大,因此我们建立筛选模型对多个指标降维。
(2)AHP层次分析求权重法
两两比较7个指标的重要程度,根据satty7级标度方法我们可以得到一致性。其中,我们将影响评价对象的指标作为一致性矩阵的行与列标题矩阵的每个元素,可以代表两两因素相比的重要程度。构造判断矩阵。
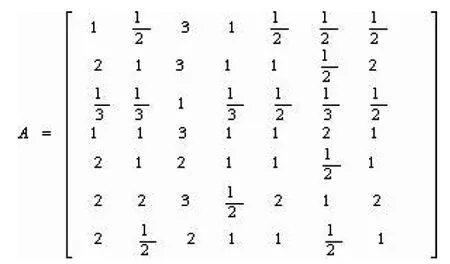
使用Matlab 程序进行计算各项权重,得
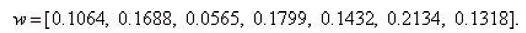
这里为了确认权重的合理性,我们进行了一致性检验。
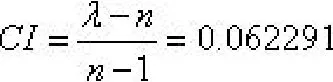
和RI一致性指标
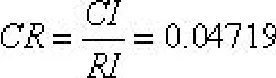
3.宜居评价值的求解
将各个指标的等级值乘上对应的权值,就可以得到各个城市宜居评价值W,W数越大,就越说明该城市宜居程度越高.得到排名由高到低,徐州、济宁、枣庄、连云港、宿州、商丘、淮北。
三、模型的改进与推广
1.模型的改进
针对多层次分析法存在的缺陷,我们可对指标与研究对象的关系进行真实值代入,减少主观因素的影响,对于不能得出最优结果的问题,我们可以尽可能地罗列满足研究对象的可能方案,扩大范围,一步步优化,进行筛选,最终得到最优秀的方案。
2.模型的推广
我们所用的模型,可以运用到描述指标或者两个知道大量数据的变量之间的关系上,得出的关系式比较精确,值得信赖;多层次分析法,可以很好地处理研究对象以及研究对象的影响因素之间的关系,使之能够迅速地建立研究对象的研究值与变量之间的关系。
四、结语
本文建立的多指标体系,逻辑清晰地说明了影响研究对象的多层指标,为没有数据的问题提供了定性分析的思路,多层次分析法,可以通过确定指标系数与现实数据,将研究对象量化,从而进行定量分析。
