我国东部典型城市年降水量和小时降水量特征分析

党皓飞 赵琳娜 王 芳廖文超 林炳青

我国东部典型城市年降水量和小时降水量特征分析

党皓飞1赵琳娜2王 芳1廖文超3林炳青1

1.福建省气象科学研究所 2.中国气象科学研究院灾害天气国家重点实验室 3.四川省南充市气象台

为探讨我国大城市降水的特征规律，利用1980～2012年6月1日至8月31日无缺测记录的北京（54511）、上海（58362）、广州（59287）三个代表站的逐小时降水资料，运用3年滑动平均法分析典型城市降水的时间分布特征；利用Γ分布函数建立概率分布模型，分析并对比三个典型城市的拟合特征。结果表明，北京、上海、广州从北向南平均降水量逐渐增大；在时间变化特征上，北京降水量呈现10年左右的波动，上海降水量无明显波动特征，广州市降水量呈现7年左右的波动。Γ函数拟合的概率分布，在一定程度上克服了样本频率代替概率不可避免的随机振荡对估计降水量概率分布的影响，用Γ分布函数概率密度推算得到的降水概率比较符合实际；Γ分布对较小量级小时降水的模拟能力比较弱，对大于5mm的小时降水模拟能力较强；三个典型城市小时降水阈值为20mm所对应的累积概率均在95%左右，因此北京、上海、广州这三个典型城市有一定概率发生较强量级的降水。

典型城市 小时降水 滑动平均 Γ分布 特征分析

1 概述

城市由于人口密集，社会经济发展快，地表硬化而渗水能力差，往往一次极端降水事件就会造成巨大人员伤亡和经济损失。如2012年7月21日，北京及其周边地区遭遇了61年来最强暴雨及洪涝灾害，根据北京市政府灾后举行的灾情通报会数据显示，此次暴雨共造成79人死亡，160余万人受灾，经济损失高达110多亿元。因此，针对不同地域的小时降雨类型及时空分布变化差异问题的研究，总结典型城市的小时极端降水特征，是提高城市防洪、排水排涝能力，减少洪涝灾害损失的重要工作。

尤焕苓等[1]使用北京地区1981～2010 年的逐日降水数据，对北京地区20个观测站极端降水的空间分布特征做了详细分析，发现该地区不同极端降水的百分位（第90、95 和99 个百分位数）阈值表现出比较相似的空间分布特征规律。王萃萃等[2]研究发现，全国半数以上的城市在1951～2005年期间平均极端降水强度呈明显增加趋势，这种结果和华北地区极端降水总的减弱趋势有明显的不同[3]，平均极端降水强度在华北东南部城市呈现显著的增大趋势。

目前，在对典型城市小时降水的研究中，主要是建立各种函数模型，从模拟和实况的比较中归纳总结出典型城市降水的一般变化规律和典型特征。例如，田付友等[4]从Γ分布入手，建立了极端形状参数α和尺度参数β的四个典型城市模型，再由特殊到一般推广至全国518个观测站，将超过95%累积概率的小时雨量作为极端小时降雨标准，进而研究超过我国极端小时降雨阈值的空间分布特征。本文将该方法运用到对北京、上海、广州三个典型城市的研究中，通过计算各典型城市降雨累积概率分布结果，归纳总结各个代表站的降水特征和一般规律。

2 资料和分析方法

2.1 资料及处理

本文使用的是由国家气象信息中心提供的国家级地面气象站逐小时降水资料，每个整点时次的降水为前一个小时降水累积量。为了研究我国典型城市降水的普遍性特点，我们选取具有代表性的北京（54511）、上海（58362）、广州（59287）三个站点，并对1951～2013年三个站点的资料进行统计处理，最终建立了1980～2012年无缺测记录的6～8月份的逐时降水资料序列。

2.2 分析方法

利用分布函数研究降水强度的气候分布特征可以抓住其较为细微和普遍的变化规律。有研究表明，Γ分布密度函数对小时降水具有很好的描述能力[5-6]。Gregory等[7]指出，有降水的地区不是有较大的形状参数就是有较大的尺度参数，而不是二者都较大。形状参数较大的地区称为“形状参数主导”区，该区域多持续降水，并且少极端天气气候事件；尺度参数较大的地区称为“尺度参数主导”区，该区域降水多变，并且多极端天气气候事件。

因此，本文使用Γ函数从概率的角度来揭示不同区域、不同强度小时降水量出现的可能性，概括出三个典型城市的夏季降水在空间分布上的一般规律。

Γ分布密度函数为：

式中，>0，>0，>0，为形状参数，为尺度参数，为小时降水量。Γ（）为Γ函数，表达式为：

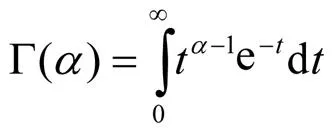
在对典型城市小时降水的研究中，利用滑动平均法分析各代表站的年代际变化，再根据Γ概率分布及其参数估计计算出三个典型城市的形状参数和尺度参数，建立北京、上海、广州的Γ概率分布模型。

3 结果分析

3.1 典型城市降水的年代际变化特征

从图1可以看出，北京地区降水量的3年滑动平均结果可以分为三个阶段：第一个阶段为1981～1983年，降水量为一个短暂的偏少型；第二个阶段为1984～1997年，降水量呈现出一个14年的偏多型，极大值出现在1995年（551.13mm）；第三个阶段为1998～2009年，降水为偏少型，极小值出现在2000年（194.7mm）；第四个阶段为2010～2011年，偏多。

从北京地区降水量累积距平（图2）可以看出，20世纪80年代初期至90年代中期降水量呈上升趋势，90年代中期至21世纪10年代呈下降趋势。在80年代中期以前低于平均降水量，80年代中期至21世纪10年代末期均高于平均降水量。1980～1984年为一个较短的平水期，1985～1996年为一个10年左右的丰水期，1998～2010为一个较长的枯水期。枯水期时段略微大于丰水期时段。

图1 北京站1980～2012年降水量和3年滑动平均降水量时间序列

图2 北京站1980～2012年降水量累积距平

从图3可以看出，上海地区降水量的3年滑动平均结果可以分为四个阶段：第一个阶段（1981～1985年）降水量为偏少型；第二个阶段（1986～2002年），除了1989年、1991年、1993年、1995年为偏少，其余时间段都为偏多型。极大值出现在2000年（753.53mm）；第三个阶段（2003～2006年），又是一个偏少型，极小值出现在2004年（357.5mm）；第四个阶段（2007～2010年）为偏少型。

上海地区降水量累积距平（图4）表明，20世纪80年代初期至90年代末期降水量呈下降趋势，90年代末期至21世纪10年代中期降水量呈上升趋势，21世纪10年代中期至21世纪10年代末期降水量又呈下降趋势。1980～1985年为枯水期，1986～1995年基本可以看作平水期，1996～2002年为丰水期，2002～2006年为枯水期，2006～2011年为丰水期。

图3 上海站1980～2012年降水量和3年滑动平均降水量时间序列

图4 上海站1980～2012年降水量累积距平

从图5可以看出，广州地区降水量的3年滑动平均结果可以分为两个阶段：第一个阶段是1981～1993年，降水量除了1982年为偏多，其余年份均为偏少型；第二个阶段是1994～2010年，除了1999年、2003年、2010年为偏少型，其余年份均为偏多型。

广州地区降水量累积距平（图6）表明，20世纪80年代至20世纪90年代初期，降水量呈显著下降趋势。20世纪90年代初期至21世纪10年代末期，降水量呈显著上升趋势。20世纪80年代中期至21世纪10年中期，降水量均低于平均值。1982～1986年和1988～1992年为显著的枯水期。1992～1997年和2003～2008年为显著的丰水期。

图5 广州站1980～2012年降水量和3年滑动平均降水量时间序列

图6 广州站1980～2012年降水量累积距平

对比图1、图3和图5可以发现，北京、上海、广州三个典型城市从北向南年平均降水量逐渐增大。1980～2012年间北京降水量呈现10年左右的波动周期；上海市降水量随机性较大，无明显的周期特征；广州市降水呈现7年左右的波动。

3.2 典型城市小时降水的Γ概率分布模拟

即为该降水阈值区间的累积概率，和分别为降水阈值的最小和最大值。

表1 各典型城市α值和β值的站点信息

Gregory等[7]的研究结果表明，在有降水发生的地区如果其形状参数较大，那么其尺度参数就很小；如果其尺度参数较大，那么其形状参数就很小；如果形状参数和尺度参数都较大，则该地区发生降水的概率就很小。形状参数比较大的区域被定义为“形状参数主导区”，在此区域内极端天气事件发生较少，持续降水发生较多；尺度参数比较大的区域被定义为“尺度参数主导区”，在此区域内极端天气事件发生较多，同时降水情况复杂多变。表1给出了各个典型城市的站点信息和形状参数、尺度参数值，可以发现三个典型城市基本上都属于尺度参数主导。

图7 北京Γ函数概率密度分布（a）、实况与拟合累积概率密度函数分布（b）

图8 上海Γ函数概率密度分布（a）、实况与拟合累积概率密度函数分布（b）

图9 广州Γ函数概率密度分布（a）、实况与拟合累积概率密度函数分布（b）

形状参数和尺度参数的分布决定了Γ分布，在求得典型城市的形状参数和尺度参数之后，对比模拟和实况发现，模拟和实况二者之间具有很好的一致性，说明Γ分布可以很好地描述小时降水的概率分布特征。图7a、图8a和图9a中柱状图为实况观测降水的频率分布，黑色曲线为根据形状参数和尺度参数获得的Γ分布。图7b、图8b和图9b为对应的实况和模拟小时降水的累积概率密度分布曲线。

对比图7a、图8a和图9a可以发现，北京小时降水主要集中在11mm以内，上海小时降水主要集中在12mm以内，广州小时降水主要集中在18mm以内。

从图7b、图8b和图9b可以发现，北京0.1mm降水的模拟累积概率为0.32，上海和广州的都在0.25左右；而三个典型城市0.1mm左右降水的实际累积概率则比较接近，都在0.52附近。这说明Γ分布对较小量级小时降水的模拟能力比较弱。随着小时降水量级的逐渐增大，模拟累积概率与实际累积概率越来越趋于一致，两条曲线基本都在累积概率为0.85附近相交，所对应的小时降水强度为5mm左右，说明Γ分布对大于5mm的小时降水模拟能力较强。

对比三个典型城市的最大累积概率模拟结果可知，上海市极端小时降水的模拟和实际结果最为接近，三个典型城市小时降水阈值为20mm所对应的累积概率均在95%以上，随后累积概率的增长速度逐渐变缓；小时降水阈值为40mm的实际累积概率为99%，但仍然有1%左右的概率发生40mm以上的降水，这也表明，北京、上海、广州这三个典型城市发生较强量级降水概率是存在的。

4 结论

（1）北京20世纪80年代初期至90年代末期降水量呈上升趋势，90年代末期至21世纪10年代呈下降趋势。上海20世纪80年代初期至90年代末期降水量呈下降趋势，90年代末期至21世纪10年代中期降水量呈上升趋势，21世纪10年代中期至21世纪10年代末期降水量又呈下降趋势。广州20世纪80年代至20世纪90年代初期，降水量呈显著的下降趋势。20世纪90年代初期至21世纪10年代末期降水量呈显著的上升趋势。

（2）北京、上海、广州从北向南平均降水量逐渐增大。1980～2012年间北京降水量呈现10年左右的波动，上海降水量无明显波动特征，广州市降水量呈现7年左右的波动。

（3）Γ函数拟合的概率分布，在一定程度上克服了样本频率代替概率不可避免的随机振荡对估计降水量概率分布的影响。用Γ分布函数概率密度推算得到的降水概率比较符合实际。

（4）Γ分布对较小量级小时降水的模拟能力比较弱，对大于5mm的小时降水模拟能力较强。三个典型城市小时降水阈值为20mm所对应的累积概率均在95%左右，北京、上海、广州这三个典型城市有一定概率发生较强量级的降水。

[1] 尤焕苓, 刘伟东, 任国玉. 1981-2010年北京地区极端降水变化特征[J]. 气候与环境研究, 2014, 19(1): 69-77.

[2] 王萃萃, 翟盘茂. 中国大城市极端降水事件变化的初步分析 [J]. 气候与环境研究, 2009, 14(5): 553-560.

[3] Zhai Panmao, Chao Qingchen, Zou Xukai. Progress in China’s climate change study in the 20th century[J]. Journal of Geographical Sciences, 2004, 14(s1): 3-11.

[4] 田付友, 郑永光, 毛冬艳, 等. 基于Γ函数的暖季小时降水概率分布[J]. 气象, 2014, 40(7): 787-795.

[5] Li L, Zhu Y J, Zhao B L. Rain rate distribution for China from hourly rain gauge data[J]. Radio Science, 1998, 33(3): 553-564.

[6] Wilks D S. Statistical methods in the atmospheric sciences[M]. California: Academic Press, 2006: 627.

[7] Gregory J Husak, Joel Michaelsen, Chris Funk. Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications[J]. International Journal of Climatology, 2007(27): 935-944.