内河船舶AIS与雷达动态信息集成性融合

2017-04-02范耀天

中国航海 2017年4期

范耀天，王驰

(1.武汉理工大学航运学院，武汉 430063；2.内河航运技术湖北省重点实验室，武汉 430063)

当前在船舶驾驶领域开展的信息融合研究主要集中在对多个船载传感器进行数据融合，支持船舶智能避碰决策方面。由于目前船舶自动识别系统(Automatic Identification System, AIS)和雷达是船舶应用的主要导航设备，因此信息融合研究主要集中在AIS与雷达的数据关联和数据融合上。这里主要研究AIS与雷达的数据融合问题。在运用统计加权法进行信息融合方面：CHANG[1]提出AIS与雷达根据误差进行数据加权融合；郑佳春等[2]将神经网络引入到统计加权估计法中提高算法的精确性，使融合后数据的准确性得到一定的改善；林长川[3]根据时间和距离作相关决策，并在一个固定的范围内获取目标，利用柯西型隶属函数进行精确的相关，提出一种改进的基于最大隶属度的融合。在基于BP神经网络算法进行信息融合方面，HU等[4]利用BP神经网络理论关联船用雷达和AIS的目标信息，对网络结构的设计进行分析，基于MATLAB进行计算机仿真。在基于卡尔曼滤波算法进行信息融合方面，于海霞[5]对雷达数据和AIS数据进行多维性分析，运用稳态卡尔曼滤波方法实现时空校准、数据关联和航迹融合，并通过试验模拟评估这些算法的稳定性及精确度。

统计加权法可提高信息融合的精度和准确性，但会间接提高算法的复杂性，且融合算法需根据数据的类型来选择；BP神经网络信息融合的网络结构参数及门限大小对结果的影响较大，且数据规模的大小对网络参数的需求不同，需在研究过程中寻找规律；卡尔曼滤波算法对实际数据的可靠性及滤波器的稳定性有一定要求，当数据的可靠性不足或滤波器的稳定性不高时，对观测值的平均值及卡尔曼滤波的估计值有很大影响。[6]集成多种融合方法可避免单一方法效果不理想的问题。

1 集成性模型

目前大多数研究主要采用单一的方法进行信息融合，主要原因是海上交通流密度不大，采用单一的方法即可满足信息关联的精度要求，而内河水域交通流密度大，交通流态势复杂，需有更高的可靠性。

由于AIS数据的中心位置是CONNING的位置，而雷达回波是一种后向反射回波，回波的位置可能是艏部、舯部或艉部，因此有必要对雷达船位进行修正。首先对雷达采集的数据进行处理，假定船体形状为椭圆形，则图1中的全球定位系统(Global Positioning System，GPS)天线位置与船舶中心位置的坐标距离为

(1)

以本船雷达天线所在位置为中心建立直角坐标系，则图2中的目标船中心位置的坐标为(M，N),船舶曲线表示为

E(x-M)2+2G(x-M)(y-N)+

H(y-N)2+f=0

(2)

若以椭圆中心点作为坐标轴原点，则椭圆的公式可表示为

(3)

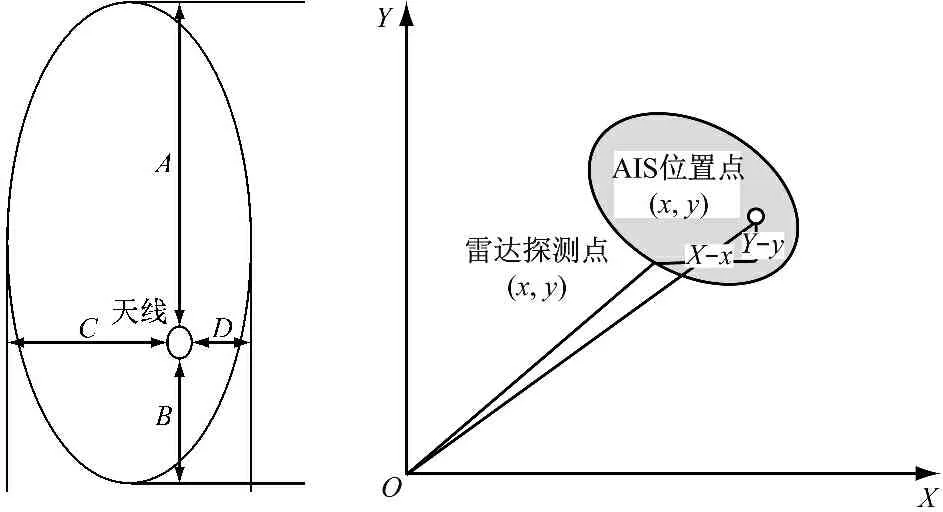
图1 船载GPS天线位置图2 雷达船位修正示意

此外，将修正后的雷达数据与AIS数据进行融合计算，构建集成卡尔曼滤波、自适应加权和神经网络等方法的多源异构数据融合模型(见图3)。

2 数据融合

近年来已有多种信息融合模型被提出，多级处理是信息融合的主要方法，其中数据融合模型分为根据节点顺序构建的功能型模型和根据数据提取构建的数据型模型2类。这里采用基于控制回路结构的混合型模型，基于信息融合处理中的循环特性，使处理任务的描述有较好的重现精度，并使融合行为发生位置容易从模型中得出；使用的方法主要包括自适应加权平均融合算法、BP神经网络融合算法及卡尔曼滤波融合算法。

2.1 自适应加权航迹融合

2.1.1最优加权因子

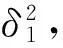
X=w1x1+w2x2

(4)

w1+w2=1

(5)

总体均方误差为

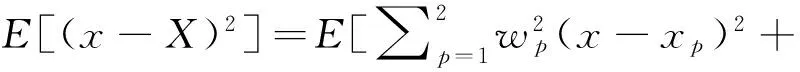
(6)

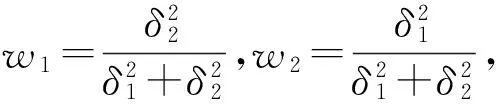
(7)

2.1.2加权融合算法

在已知AIS和雷达的测量方差及加权因子的情况下，可得到各自融合后的方差和融合之后的距离、方位、对地航速及航向，即

(8)

(9)

Xij(k)=wadXAi(k)+wrdXRi(k)=

(10)

Yij(k)=waθXAi(k)+wrθXRi(k)=

(11)

2.2 BP神经网络融合

2.2.1融合模型的建立

分别设置网络的输入和输出，隐含节点、网络目标的误差、训练次数及学习率，并代入训练数据进行训练。[7]构建好融合模型后，首先对网络进行训练，使网络达到设置要求，然后输入关联的AIS和雷达数据，得到网络输出的合并信息。[8]

2.2.2网络的测试和验证

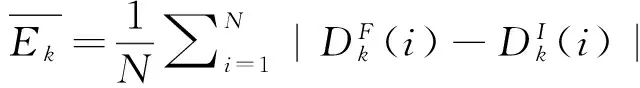
2.3 卡尔曼滤波融合

对雷达和AIS进行融合的基本原理是在空间上和时间上依据某种准则对2台传感器的信息进行结合，得到一个更合理、精度更高的融合数据，使之拥有比单传感器更高的精准度。卡尔曼状态估计的功能可实现对雷达和AIS的数据进行平滑，对所测的船舶数据进行滤波和对船舶未来的航行轨迹进行预测。卡尔曼滤波理论是依据状态方程工具应用时域法递推得出最优估计值。[10]

这里进行数据融合，对目标的状态估计可表示为

I-K(k+1)H(k+1)=

P(k+1|k+1)P(k+1+k)-1

(12)

对雷达和AIS，都有

Hi(k+1)=Pi(k+1|k+1)Pi(k+1+k)-1

(13)

(14)

由此可得

(15)

(16)

Pi(k+1|k+1)-1=Pi(k+1|k)-1+

(17)

P(k+1|k)=Φ(k)P(k|k)Φ(k)′+

G(k)Q(k)G(k)′

(18)

3 集成性融合

3.1 数据集成性融合

利用不同方法得出的融合数据与真实数据可能相差较大，分别比较3种融合方法的融合数据与真实数据的误差大小，运用加权平均法得出3种融合方法的加权权重，得出最终的融合数据。由加权平均公式可得3种融合方法的权重大小。

(19)

(20)

(21)

(22)

(23)

(24)

根据加权平均公式可得自适应加权航迹融合法的x坐标权重和y坐标权重分别为ωx1=σ2+σ3/2[(σ1+σ2+σ3)]及ωy1=(δ2+δ3)/(δ1+δ2+δ3)；BP神经网络融合的x坐标权重和y坐标权重分别为ωx2=σ1+σ3/[2(σ1+σ2+σ3)]及ωy2=(δ1+δ3)/[2(δ1+δ2+δ3)]；卡尔曼滤波融合的x坐标权重和y坐标权重分别为ωx3=σ1+σ2/[2(σ1+σ2+σ3)]及ωy3=(δ1+δ2)/[2(δ1+δ2+δ3)]。

航迹融合可表示为

(25)

(26)

式(25)和式(26)中：xaw(k)为k时刻自适应加权航迹融合航迹点x坐标；xBP(k)为k时刻BP神经网络融合航迹点x坐标；xkm(k)为k时刻卡尔曼滤波融合航迹点x坐标；yaw(k)为k时刻自适应加权航迹融合航迹点y坐标；yBP(k)为k时刻BP神经网络融合航迹点y坐标；ykm为k时刻卡尔曼滤波融合航迹点y坐标。

3.2 集成系统精确性和稳定性

3.2.1精确性

分别定义k时刻的自适应加权融合航迹点坐标为(xaw(k)，yaw(k))，BP神经网络融合航迹点坐标为(xBP(k)，yBP(k))，卡尔曼滤波融合航迹点坐标为(xkm(k)，ykm(k))，集成融合航迹点的坐标为(xt(k)，yt(k))，真实航迹点的坐标为(x(k)，y(k))；误差的波动性低,则融合精度高。误差的波动性计算式为

(27)

(28)

自适应加权融合的精确性可表示为

(29)

BP神经网络融合的精确性可表示为

(30)

卡尔曼滤波融合的精确性可表示为

(31)

集成性融合的精确性可表示为

(32)

3.2.2稳定性

航迹融合的稳定性即相邻航迹点之间的差值大小Δk的总和。

(33)

(34)

自适应加权融合的稳定性可表示为

(35)

BP神经网络融合的稳定性可表示为

(36)

卡尔曼滤波融合的稳定性可表示为

(37)

集成性融合的稳定性可表示为

(38)

4 模拟及验证

为充分体现内河船舶的航行特点，不仅应收集实船直线航行时的雷达和AIS数据，还应采集船舶大幅度机动时的数据。由于内河水域船舶操纵空间具有一定的局限性及在内河水域复杂环境下进行船舶试验可能引发事故，因此模拟验证的数据收集选择在白天能见度良好的沿海开阔海域进行。由于大型船舶在转向和变速方面较为迟钝，同时为保证试验的安全性和维护正常的航行秩序，试验船舶采用操纵灵活的引航艇，试验航线为从山东青岛大港六号码头至胶州湾团岛附近航段。试验过程具体为：2015年11月5日以青岛港引航站的“引航2号”船作为目标船，在青岛舶舶交通管理中心(Vessel Traffic Services,VTS)以VTS雷达模拟本船雷达，实时跟踪“引航2号”船的运动，并收集目标船及附近船舶的经纬度、航速和航向等AIS及雷达数据；同时，在目标船上安装差分全球定位系统(Differential GPS,DGPS)，其天线架设在目标船自有的GPS天线附近，对其经纬度、航速及航向数据进行测量和采集。由于DGPS的精度较高，在后续的验证阶段，信息融合模型以目标船舶的DGPS数据作为基准数据进行比对。

通过数据关联得到与AIS相关联的雷达数据，根据第“3”节中提出的3种融合方法及公式对试验采集到的AIS数据和雷达数据进行计算，得到航迹加权法x坐标和y坐标的误差平方和分别为σ1=1 972.342及δ1=8 245.462，BP神经网络x坐标和y坐标的误差平方和分别为σ2=4 624.231及δ2=26 235.791，卡尔曼滤波的x坐标和y坐标的误差平方和分别为σ3=4 245.348及δ3=26 682.496。

根据加权平均公式可得：

1) 自适应加权航迹融合法的x坐标和y坐标权重分别为ωx1=0.409 0及ωy1=0.432 5。

2) BP神经网络融合的x坐标和y坐标权重分别为ωx2=0.286 7及ωy2=0.285 5。

3) 卡尔曼滤波融合的x坐标和y坐标权重分别为ωx3=0.304 2及ωy3=0.281 9。

由此,航迹融合可表示为

xr=0.409 0xaw(k)+0.286 7xBP(k)+

0.304 2xkm(k)

(39)

yr=0.432 5yaw(k)+0.285 5yBP(k)+

0.281 9ykm(k)

(40)

5 结束语

本文分析了内河船载雷达和AIS在船舶动态感知及辨析中的局限性及互补性，构建了集成AIS和雷达的多源异构数据融合模型，通过算例验证了该模型可在保证模型可靠性的基础上大大提高模型的精确性和稳定性。

[1] CHANG S J. Development and Analysis of Applications as an Efficient Tool for Vessel Traffic Service[C]//Oceans,2004,4(4):2249-2253.

[2] 郑佳春,陈宗恒.基于模糊神经网络的AIS与雷达目标数据融合[J].集美大学学报,2005,10(3):216-220.

[4] HU X, LIN C. A Preliminary Study on Targets Association Algorithm of Radar and AIS Using BP Neural Network[C]//Procedia Engineering, 2011:1441-1445.

[5] 于海霞.AIS与雷达数据融合方法的研究[D].大连:大连海事大学,2006.

[6] 刘庆华，仲海啸，陶峰，等. 卡尔曼滤波融合新算法及其船舶高精度液位测量的应用[J].中国造船, 2016, 57(2):192-200.

[7] 郭文刚. 基于BP神经网络的船舶航迹控制技术[J]. 舰船科学技术, 2014(8):87-93.

[8] 胡晓瑞. 基于BP神经网络的雷达与AIS目标信息融合处理研究[D]. 厦门：集美大学，2012.

[9] 张莉. BP神经网络在船舶运动估计中的应用[J]. 舰船科学技术, 2016(12):13-15.

[10] 徐铁，蔡奉君，胡勤友，等. 基于卡尔曼滤波算法船舶AIS轨迹估计研究[J]. 现代电子技术, 2014(5):97-100.