曲线之间的滚动*
2017-04-01杨洁
杨 洁
(湖州师范学院理学院 浙江 湖州 313000)
邱为钢
(湖州师范学院理学院 浙江 湖州 313000;湖州师范学院物理视觉工作室 浙江 湖州 313000)
曲线之间的滚动*
杨 洁
(湖州师范学院理学院 浙江 湖州 313000)
邱为钢
(湖州师范学院理学院 浙江 湖州 313000;湖州师范学院物理视觉工作室 浙江 湖州 313000)
把滚动分解为质心平动和绕质心的转动.由约束条件,给出了圆弧组成的叶状物在正三角形和正方形内滚动时,以及内摆线在另一个内摆线滚动时,质心位置和转动角的参数方程.由这些表达式,给出了滚动物体上特殊点的轨迹.
滚动 内摆线 轨迹
一个曲线沿着另一个曲线(一般固定)滚动,滚动曲线上或内(外)一点,依据这两个曲线形式和滚动模式,会形成多种多样的轨迹.如果固定曲线是直线,滚动曲线是椭圆,滚动模式是纯滚动,那么滚动椭圆上一点会形成椭圆旋轮线[1].如果固定曲线是圆,滚动曲线也是圆,两个圆半径之比是有理数,滚动模式是纯滚动,那么滚动圆上一点会形成内(外)摆线[2].本文考虑两个曲线都是封闭曲线之间的(非纯)滚动模式.运动学上滚动可以分解为质心平动与绕质心的转动,由于约束条件,质心位置(或平移量)可以表示为转动角的参数方程.依据质心位置转动角的表达式,就可以把滚动曲线上(外)任意一点的轨迹表示出来.为简单起见,本文只考虑3种情况:两段圆弧组成的封闭曲线在一个正三角形内滚动;三段对称圆弧组成的封闭曲线(莱洛三角形)在一个正方形内滚动;内摆线在一个内摆线内滚动.
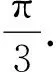
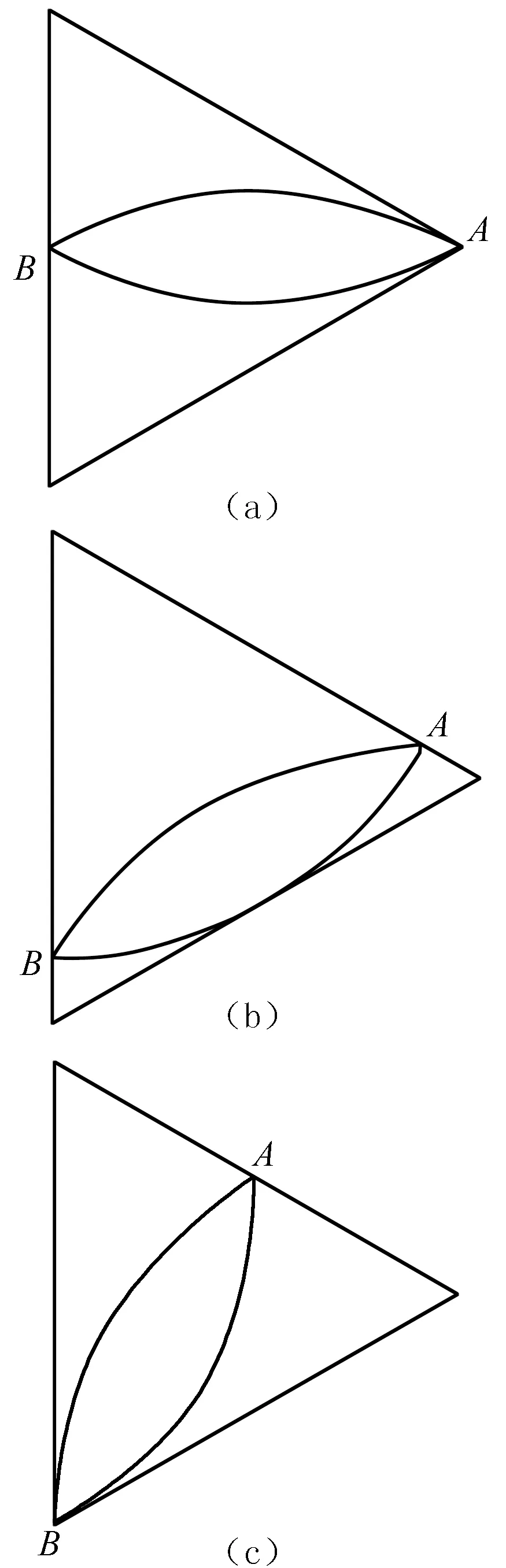
图1 双叶在正三角形内的滚动
从对称性考虑,以正三角形的中心为坐标原点,正三角形的外接圆半径是4,A点的起始坐标是(4,0),B点的起始坐标是(-2,0),双叶质心坐标是(1,0).双叶上下两段圆弧起始时刻相对质心的参数坐标分别是
(1)
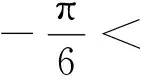
(2)
双叶滚动后,A点和B点仍旧在三角形的两条边上.计算得到(省略过程)质心平移量与转动角度的关系式
(3)
(4)
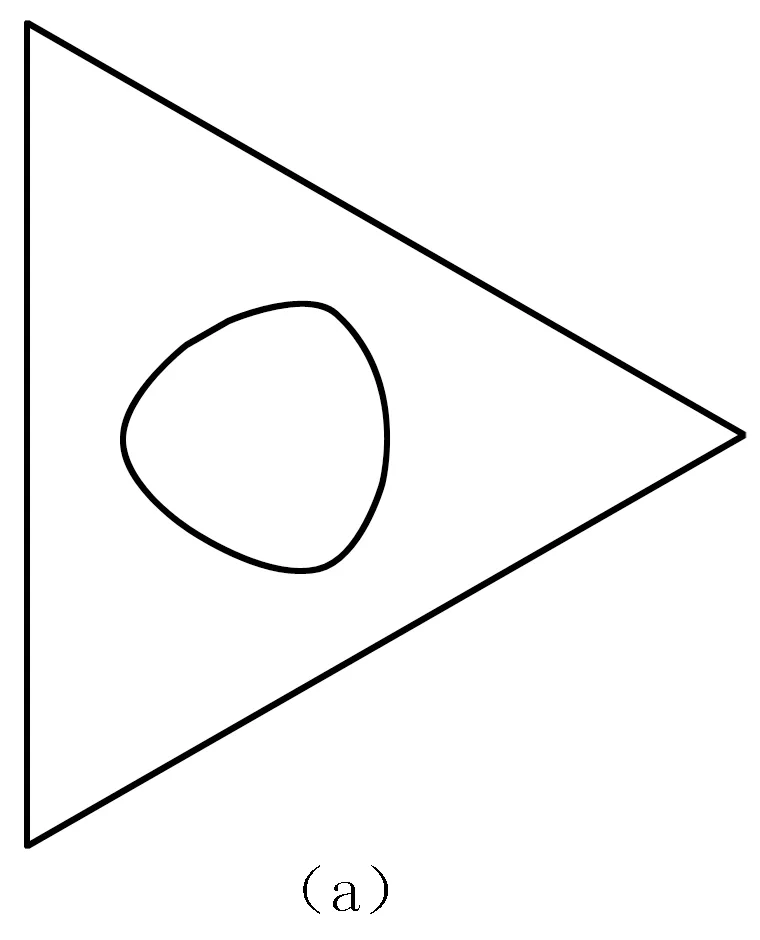
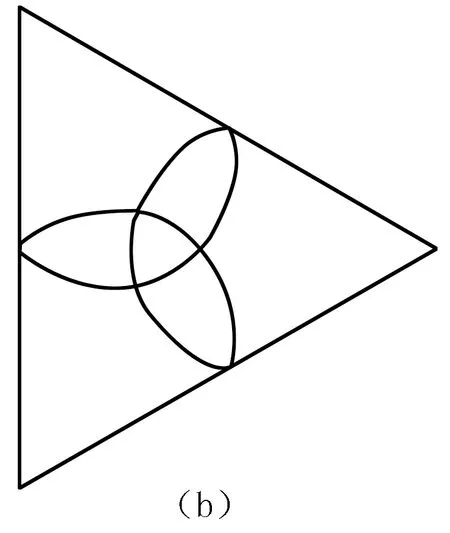
图2 双叶质心和圆弧中点轨迹
质心表达式(3)和(4)其实是椭圆弧,所以双叶上任意固定一点的轨迹由3段对称的椭圆弧组合而成,这从图2上可以看出来.

图3 三叶在正方体内的滚动

(5)
(6)
(7)
随后,三叶质心平移(xc,yc),然后整体逆时针转动θ角度.三叶滚动后,两个端点E和F仍旧落在正方形边上.计算得到质心平移量与转动角度的关系式
(8)
(9)
质心表达式(8)和(9)其实是椭圆弧,所以三叶上任意固定一点的轨迹由4段对称的椭圆弧(与质心的椭圆弧不一样)组合而成,这从图4上可以看出来.

图4 三叶质心和圆弧中点轨迹
第三种情况如图5所示,是一个三叶内摆线在另一个四叶内摆线内的滚动.
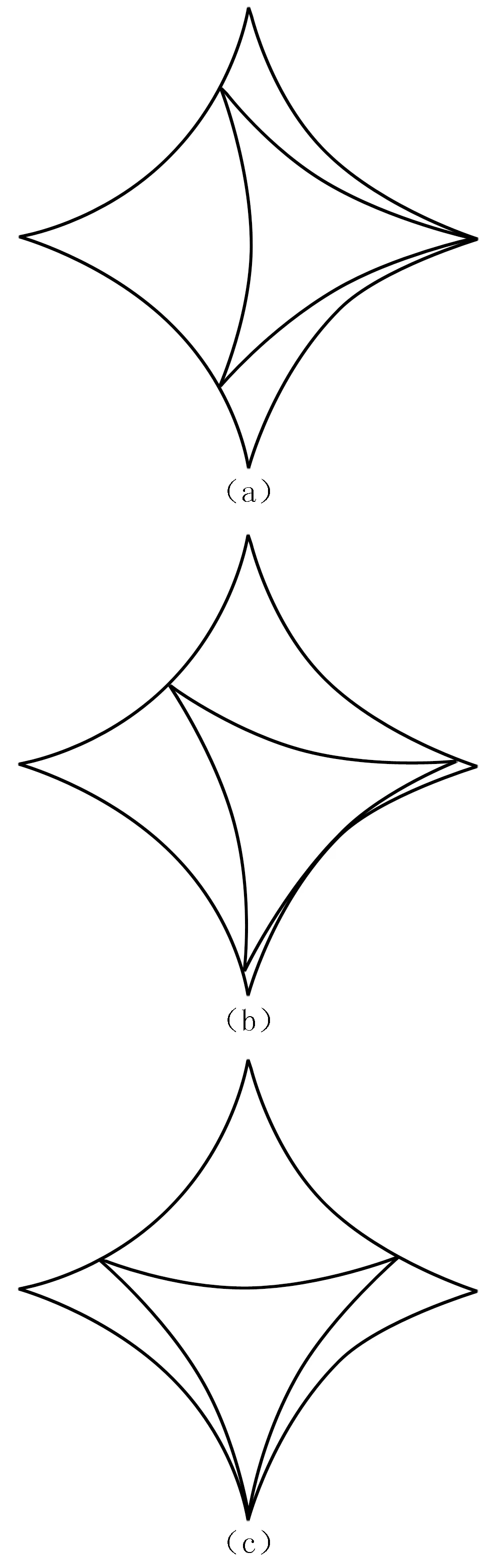
图5 三叶内摆线在四叶内摆线内的滚动
内摆线可以看作一个小圆在一个大圆内纯滚动时,小圆圆周上固定一点的轨迹.如果大圆半径为R,小圆半径为r,以大圆圆心为坐标原点,那么内摆线复数形式的参数方程是[4]
(10)
设3个圆的半径分别为r1,r2,r3.小的内摆线是第一个圆在第二个圆里面滚动形成的,它相对第二个圆圆心的参数方程是
(11)
这个内摆线随着第二个圆一起在第三个圆内滚动,由复数加法和乘法意义,加法代表平移,乘法exp(iθ)表示转动,转动角为θ.设第二个圆质心平移后的复数坐标是u,那么滚动后摆线的参数方程是
(12)
滚动后摆线上一点要落在第二个内摆线上.第二个摆线由第一个圆在第三个圆内滚动而成,复坐标具有以下表达式
(13)
式(11)和式(12)应该相等.假定平移后第二个圆质心复坐标有这样的形式u=(r3-r2)exp(iφ),对比式(11)和(12),得到参数角与转动角的关系式
(14)
取半径为(1,3,4),就得到图5中的图形.取半径为(1,3,5),就得到图6中的图形.

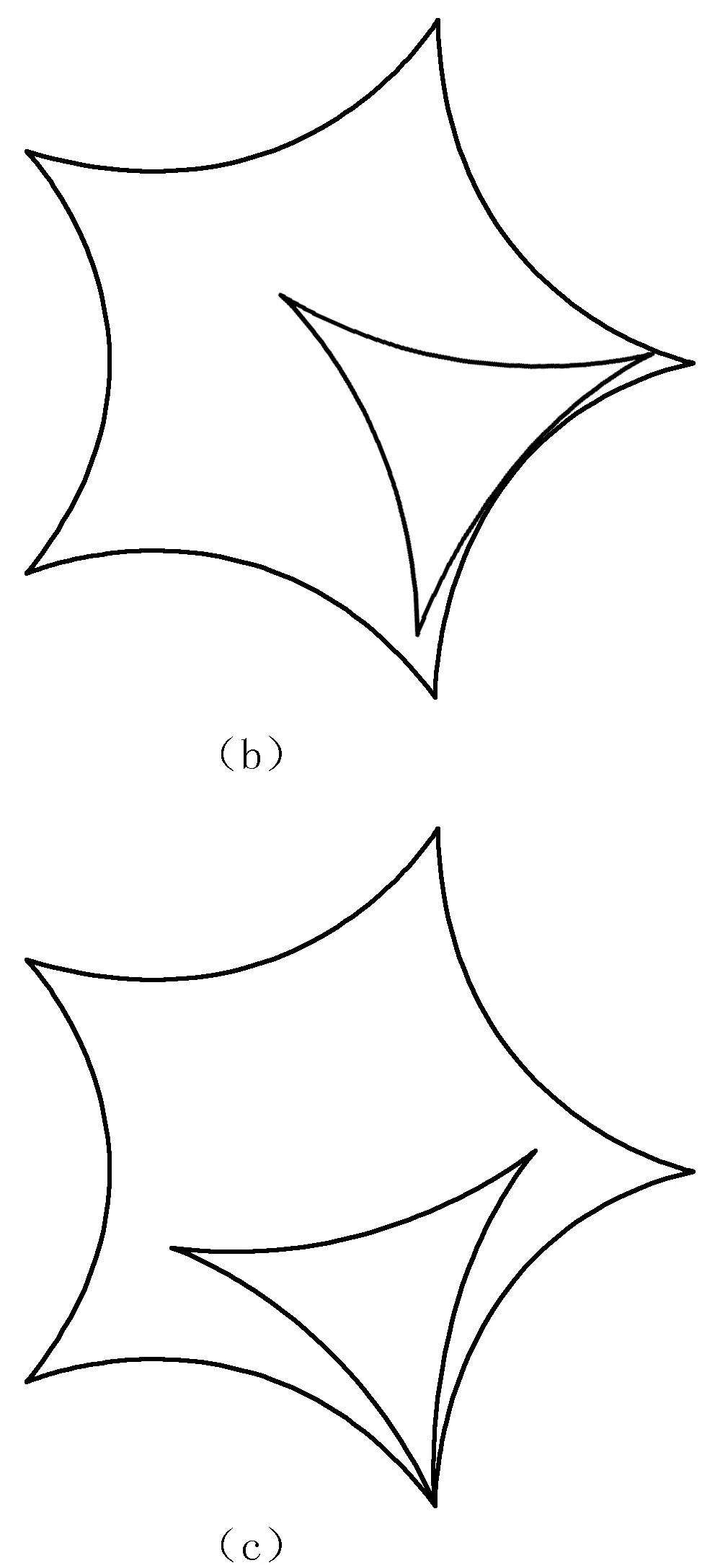
图6 三叶内摆线在五叶内摆线内的滚动
由以上平移和转动表达式,还能得到三叶内摆线在五叶内摆线内滚动时,尖点和“弧线”中间点的滚动轨迹,如图7所示.
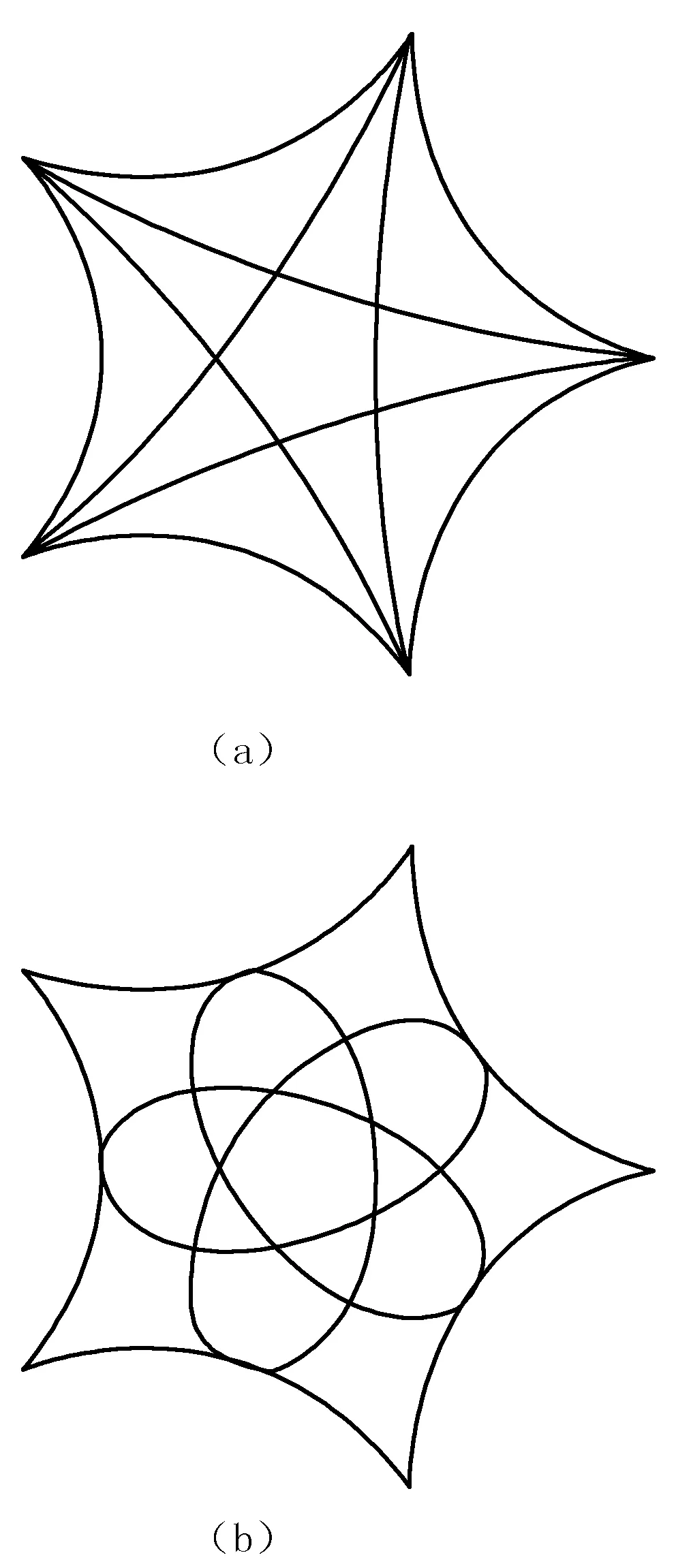
图7 三叶内摆线尖点和弧线中点的滚动轨迹
这样,利用运动学分解和约束条件,得到了质心平移量(或位置)与绕质心转动角的解析表达式,并给出了物体上特殊点的滚动轨迹.这种方法也能求其他曲线之间的滚动轨迹,不再详述.
1 陶涛,邱为钢.椭圆旋轮线.大学物理,2013,32(1):33~34
2 佘守宪, 唐莹.浅析物理学中的旋轮线(摆线).大学物理,2001,20(6): 5~10
3 莱洛三角形. http://mathworld.wolfram.com/Reuleau- xTriangle.html
4 摆线. http://mathworld.wolfram.com/Hypocycloid. html
The Rolling Motion between Curves
Yang Jie
(Department of Physics, Huzhou Teachers College, Huzhou, Zhejiang 313000)
Qiu Weigang
(Department of Physics, Huzhou Teachers College, Huzhou, Zhejiang 313000;Physical Visual effects studio, Huzhou Teachers College, Huzhou, Zhejiang 313000)
A rolling motion is composed of displacement of center of mass (COM) and rotation around COM. From constraint condition, the rotation angle parametric expressions of displacement of COM are given for two kind of rolling motion between two curves: a leaf-like body made of arcs rolling inside a regular triangle and a square and a hypocycloid rolling inside another hypocycloid. The orbits of some special point on the rolling body are also given.
rolling motion; hypocycloid; orbit
*高等学校力学课程教学研究项目,项目编号:JZW-15-LX-15;湖州师范学院教改项目,项目编号:JGB16022;国家自然科学基金,项目编号:11475062
杨洁(1995- ),女,在读本科生.
邱为钢(1975- ),男,博士,副教授,主要从事大学物理的教学研究工作.
2016-10-10)
