面向工程的模块化多电平换流器建模与仿真

摘要：作为第二代高压直流输电技术的核心技术，模块化多电平换流器（modular multilevel converter，MMC）以半桥子模块（Sub modules，SM）为基本单元，能用较低的开关频率实现交直流间的高效转换，具有谐波含量低、损耗小的优势。但MMC单桥臂采用的SM数量超过400个，仿真采用精确建模的方法，对计算机资源需求很高，且仿真时间长，不利于MMC主电路以及保护设计参数的验证和修正。本论文基于梯形积分理论，利用等效电阻模拟IGBT的开关过程，在传统戴维南等效电路的分析基础上，通过状态空间分析理论建立MMC每个桥臂的等效诺顿电路，对传统算法进行了改进，在提高MMC的仿真速度的同时，还能够真实反映每个SM的工作状态，最后与MMC详细建模仿真得到的结果进行比较，验证本方法的有效性和正确性。

关键词：模块化多电平换流器 电磁暂态模型 梯形积分理论 诺顿等效电路

中图分类号：TP391.9 文献标识码：A 文章编号：1007-9416（2016）10-0055-04

1 引言

传统高压直流输电采用的是电压源变流器技术，由于这种多电平变流器控制复杂、制造和工程实践难度大，实际运行的装置多使用二极管箝位的二电平或三电平变流器，输出谐波含量较大，为保证电能质量满足要求，需配有较大容量的滤波器，损耗较高。通常，变流后输出电压的电平数量越多，谐波含量越少，若同时能以较低的开关频率实现，则损耗也能够控制在较低的水平。为此，2001年文献[1]中首次提出了MMC技术，这种基于串联半桥模块的技术，克服了高压输电电压高与电力电子器件耐压低之间的矛盾，也克服了变流过程中谐波大、损耗高的缺陷。当电压等级提高时，无需复杂的控制，只需要简单的增加SM的数量，就可以保证装置的可靠运行，是目前最具前景的高压直流输电技术。

实际工程中，MMC单个桥臂采用的SM数量已经超过400个，考虑到SM器件均压、驱动以及整个系统的保护，通过电路仿真详细的模型然后再使用计算机计算，时间长，以320kV单极运行直流输电为例，仅双端电源、输电线路换流器及其控制部分，在I7 4790k主频4.5GHz，16G/2.4GHz内存的计算机上，仿真步长40μs，对运行3s的直流线路进行故障仿真以验证保护是否正确动作，需要的机器时间5077s，更复杂的电力系统时，如多端MMC直流输电线路，仿真时长将达到数千小时[2]。修改一次参数都要重新仿真，降低工程设计效率。因此需要在满足MMC装置控制和运行特性的前提下，满足工程误差允许内，简化MMC仿真模型，降低仿真所需時间。

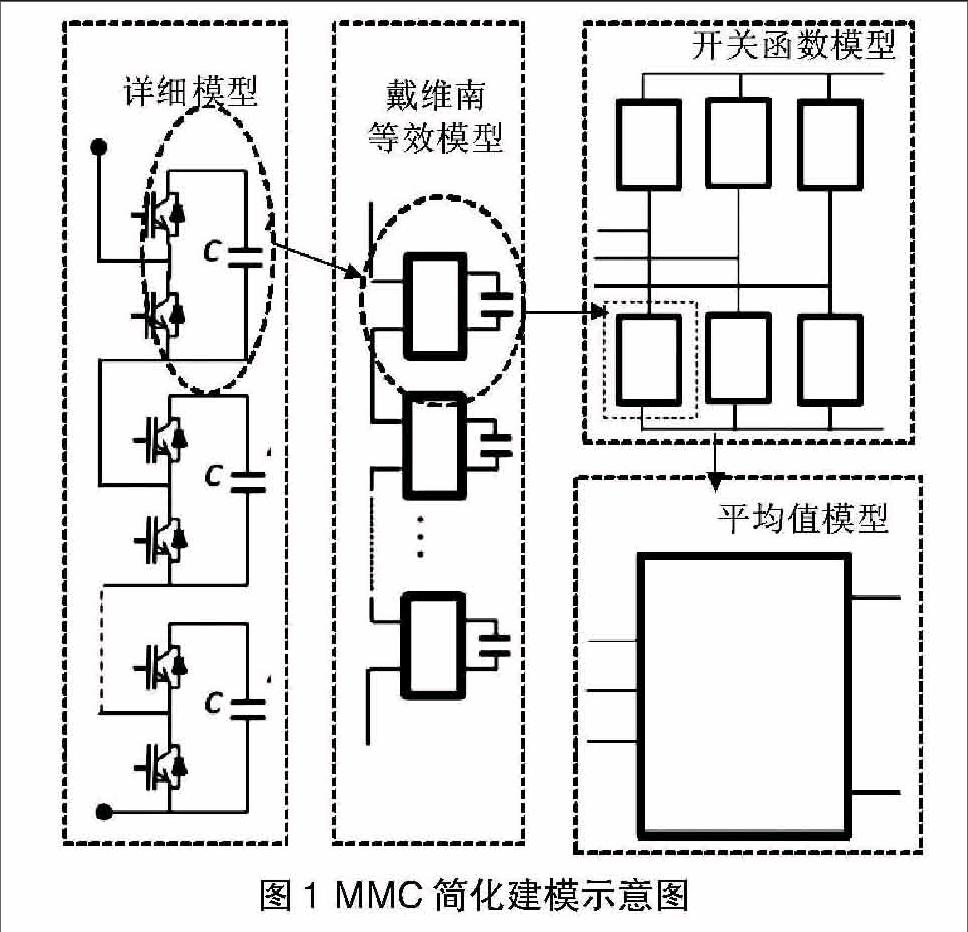
目前MMC简化模型有许多研究，最新研究主要分为三类，如图1所示。

（1）戴维南电路的等效模型，通过子模块电力电子电路的简化加速仿真速度，但每个SM的运行状态准确获取的难度较大[3][4]；（2）开关函数模型，忽略桥臂内SM的串联均压关系，将桥臂简化为一个开关器件，但该方法无法研究MMC故障时其内部模块的保护，是仿真速度非常快的方法；（3）平均值模型，与开关函数模型类似，同样忽略了内部SM连接方式，交流侧和直流侧分别用可控电流源和电压源代替，是仿真速度最快的方法，缺点与开关函数模型一样[5]。戴维南等效电路的模型比较符合需求，除了可以仿真MMC正常时的运行特性，也可以仿真故障时的保护特性，而开关函数模型和平均值模型主要用于研究MMC的谐波和功率输出特性。戴维南电路的等效模型应用较多，但子模块数量没减少，计算效率还有优化空间。

本文提出了一种状态空间离散电路分析方法，对上述模型进行改进：引入通断电阻，采用诺顿等效的方法进一步简化了戴维南等效后每个桥臂的模型，利用电磁暂态算法中的梯形积分原则，用等效历史电流源和并联电阻代替SM中的电容，基于离散状态空间分析将每个桥臂简化成等效离散诺顿电路，既保留了每个SM的状态空间特性，使得仿真过程每个SM的电气量均保存在计算结果中，又有效降低仿真电路中的节点数量，提高仿真速度。最后对MMC简化模型与详细建模的仿真进行对比。

2 MMC离散化SM戴维南等效模型分析

MMC电路拓扑结构如图2所示，每个桥臂由N个子模块组成。

每个子模块的详细模型和4种开关状态，如图3。K1高速短路开关在SM非正常触发时起保护作用；K2晶闸管检测到故障电流时导通用于保护SM中的IGBT模块不损坏。

正常工作时，每个SM均由门级信号g1i和g2i控制（i表示SM的编号），交替导通，SM的电压VSMi等于电容电压Vci；还有一种特殊状态是MMC启动或者故障时，SM的两个门极信号均为关闭状态，此时VSMi取决于此时电流的流向，可能为图3（b）中的1或4，处于这种状态时，SM中的电容仅能通过二极管S1i充电，无法放电。

SM详细建模时，需要用理想可控开关、考虑VI特性的二极管以及缓冲电路模拟IGBT器件，能够真实的反映IGBT处于开关状态时的非线性特性，这在原型机验证时非常重要，但在工程应用时完全可以忽略IGBT的非线性对实际运行的影响。为了简化上述模型，本文使用开关电阻Ron和Roff代替IGBT模拟SM的工作状态，如图4（a）所示，图中R1i和R2i为第i个SM的开关电阻，当IGBT导通时值为Ron，截止时为Roff。

根据隐式梯形积分理论[6]，若时间步长为，则此时SM中的电容可以等效为图4（a）中电流源和电阻RC（）并联，上标h表示时间为时的历史值，图4（a）可等效为图4（b）的电压源和RC串联。则单个桥臂的电压为所有SM电压之和，即

则电路可继续简化，如图4（c）所示。

其中第i个SMi等效电阻为，

传统的戴维南等效法虽然能将MMC桥臂简化为电阻和电压源串联的3节点电路，但等效过程中忽略了每个SM的运行特性，因此只能用于研究MMC的谐波和功率输出特性，无法研究内部SM模块的均压或保护等问题。

3 MMC桥臂诺顿等效模型及其算法实现

为了改进MMC桥臂传统戴维南等效分析方法，本文提出的诺顿等效电路降低了MMC每个桥臂的节点数量，从3节点降低为2节点，同时与该电路配合的算法还可以保留每个SM的输出状态。

3.1 MMC桥臂诺顿等效模型

根据状态空间节点法[7]，任何一个线性电路的输入输出关系均可以用式（5）表示，

由式（7）可知，若yt表示某时刻线性电路中的输出电流，上式等號右边第一项可表示为历史电流源，而第二项可以表示为恒阻抗与电压源的乘积。因此可将式（1）转换成诺顿电路的表现形式，

可得到MMC桥臂诺顿等效电路，如图5所示。

3.2 MMC桥臂等效电路的算法

MMC每个桥臂等效为诺顿等效电路，但是每个桥臂的电压和电流在等效过程中均存储在仿真结果中，因此也就保存了每个SM的工作特性，相比传统戴维南简化电路无法获知每个SM特性而言，是重大的改进。由于采用开关电阻等效，仿真时长相比详细建模极大的减小，算法实现如下：

（1）利用式（8）将初始电压代入，根据开关的初始状态，计算出桥臂电流。

（2）根据触发信号状态，调整图4中每个SM的R1i和R2i值：当SM为导通状态，则R1i=Ron，R2i=Roff；当SM为截止状态，则R1i= Roff，R2i=Ron；当SM为启动或故障运行状态，若iarm大于零，且vSMi大于vCi，则等同于SM导通状态，若iarm和vSMi均小于零，则等同于SM截止状态，其余状态均视为R1i=R2i=Roff。

（3）计算图4中通过每个SM电容的电流和端电压：

（4）利用式（2）以及式（3）计算SM戴维南等效电路中的和。

（5）利用式（1）计算每个SM的电压和桥臂的总电压。

（6）利用式（8）-（10）计算MMC每个桥臂诺顿等效电路中的和桥臂电流。

（7）返回步骤1，将此次计算中得到的作为下次计算的初始电压，重复步骤2到7直到仿真结束。

4 仿真验证

为了验证本文所提方法的有效性，在EMTP软件中搭建了MMC单极运行的详细建模和诺顿等效仿真模型，两端对称配置，仿真模型如图6所示，以送端为例。即400kV电源经主断路器与YD11降压变压器连接，在于与MMC主电路之间设置涌流抑制断路器BK2限制启动时的充电电流，与其并联的电阻设置为1000Ω，待稳定后合上断路器BK2短接限流电阻。送端MMC经70km直流电缆输送到受端，并在受端电源处设置三相对地短路故障。总仿真时长为3s，运行1.5后发生故障，持续0.2s。

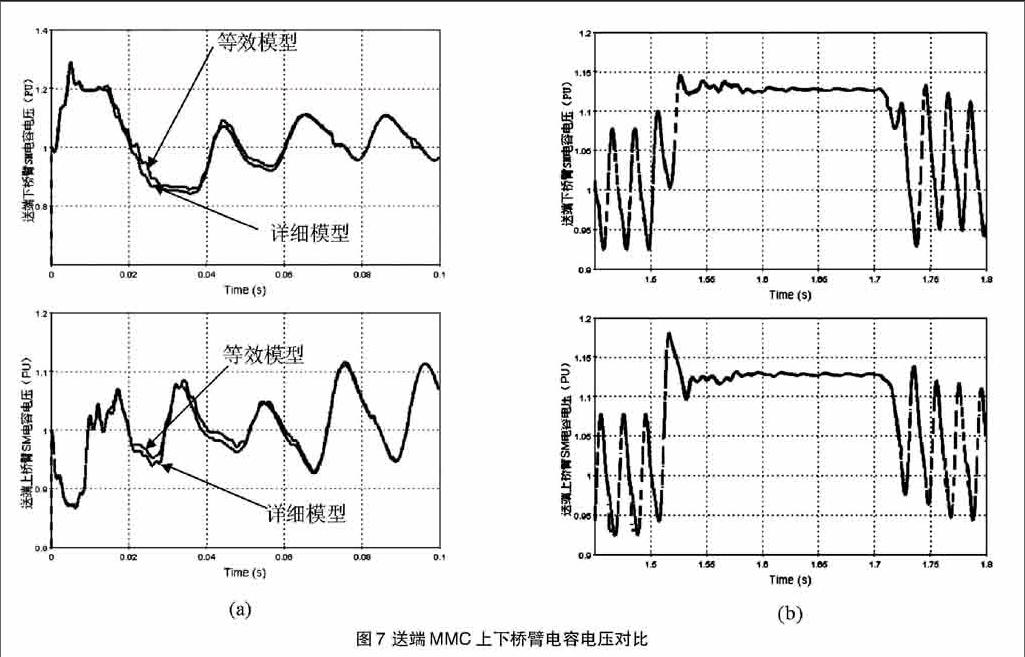
基于诺顿等效的模型在176s后得到运行结果，相比详细建模提高了29倍，送端MMC上下桥臂电容电压在装置启动时和故障时的仿真对比如图7所示。

等效模型在两种工况下的波形与详细模型基本一致，能够正确的反映每个SM的电容运行状态。

篇幅限制，波形比较不全部罗列，上述仿真结果已经能够满足工程对MMC仿真快速性和准确性的要求。大幅度提高了MMC的仿真速度，仿真结果误差小。

5 结语

本文基于诺顿等效电路，提出和实现了一种MMC电磁暂态建模方法，算法实现简单易于实现。仿真算法所需的节点数相比传统的戴维南等效建模方法更少，在仿真速度上相比SM详细建模建立的MMC模型提高了29倍，同时还解决了传统的戴维南等效建模方法无法正确反映各SM工作状态的难题，仿真结果准确。本文所提出的模型更具有工程实用意义，为实际中MMC的运行、保护整定和参数设定提供了研究平台，为MMC的推广应用奠定了良好基础。

参考文献

[1]Lesnicar A，Marquardt R.An Innovative Modular Multilevel ConverterTopology Suitable for a Wide Power Range[C].2003 IEEE Bologna Power Tech Conference. Bologna，Italy： IEEE，2003.

[2]徐建中.模块化多电平换流器电磁暂态高效建模方法研究[D].北京：华北电力大学，2014.

[3]Udana N.Gnanarathna， Aniraddha M.Gole，and Rohitha P. Jayasinghe， Efficient Modeling of Modular Multilevel HVDC Converters （MMC） on Electromagnetic Transient Simulation Programs，IEEE Transactions On Power Delivery， vol. 26，no. 1，pp： 316-324， Jan. 2011.

[4]管敏渊，徐政.模块化多电平换流器的快速电磁暂态仿真方法[J].电力自动化备，2012，32（6）：36-40.

[5]J. Peralta，H.Saad， S.Dennetière，J.Mahseredjian and S. Nguefeu，“Detailed and Averaged Models for a 401-level MMC-HVDC system”IEEE Trans.on Power Delivery，vol.27，no.3，July 2012，pp.1501-1508.

[6]H Dommel，Electromagnetic Transients Program Theory Book[M]， Bonneville Power Administration，1986.

[7]C.Dufour，J.，Mahseredjian，J.，Belanger，A Combined State-Space Nodal Method for the Simulation of Power System Transients， IEEE Transactions on Power Delivery，vol.26，no，2，pp.928-935，2011.

收稿日期：2016-09-05

作者简介：郭洪英（1970—），男，回族，福建惠安人，硕士，高级工程师，研究方向：高压输变电工程建设与管理；陈章山（1975—），男，汉族，福建福

清人，本科，中级工程师，研究方向：高压电气试验。