决策树ID3算法及其改进

杨洋

摘 要：介绍了数据挖掘的相关概念，数据挖掘中决策树ID3算法的相关概念以及信息增益和信息熵概念。通过实例介绍了ID3算法的主要内容，指出了ID3算法的不足及改进之处。针对该实例提出ID3算法的一种改进算法——MIND算法，并通过MIND算法重新计算实例内容。最后通过实例分析将改进算法与ID3算法进行对比，证明了改进算法的有效性。

关键词关键词：数据挖掘；决策树；ID3算法；MIND算法

DOIDOI：10.11907/rjdk.161585

中图分类号：TP312

文献标识码：A 文章编号：1672-7800（2016）008-0046-03

0 引言

ID3算法属于决策树算法当中的一种，它是通过把实例从根结点排列到某个叶子结点来对实例进行分析，叶子结点即为实例所属的分类[1]。决策树上的每一个结点就是对该实例某一个属性的测试，并且该结点的每一个后继分支对应着该属性的一个可能值。分类从根节点开始，对所有的实例通过所选属性进行分割，属性的选择采用最高信息增益法。停止分割的条件是：没有属性可以再对实例进行分割，或者结点上的实例都属于同一目标属性类别。ID3算法主要针对属性选择问题，是决策树学习方法中最为典型的算法，该方法使用信息增益度选择测试属性。

MIND算法可以作为ID3算法的一种改进算法，其算法思想更方便考虑每一个概化数据元组。MIND算法是一种典型的决策树构造方法的构造分类器，是采用数据库中用户定义的函数UDF发现分类规则的算法，也就是在决策树的每一层，为每个属性建立一张维度表，用来存放各个属性的取值属于哪个类别及结点编号，其优点是通过采用UDF实现决策树的构造过程使得分类算法易于与数据库系统集成。

1 数据挖掘

数据挖掘这个概念于1989年提出 [2]，指从大量模糊的、有噪声的、不完全的、随机的数据中挖掘出有价值的信息。随着信息技术的发展，大数据技术广泛应用，数据挖掘发挥着越来越重要的作用。在数据挖掘中人们对 “啤酒与尿布”的经典案例津津乐道：在美国超市，研究人员发现啤酒和尿布的销量总成某种特殊的关联关系，原来当父亲来到超市给孩子买尿布时，总会捎带啤酒。根据这个发现，超市工作人员特意将啤酒和尿布这两个看似毫不相干的商品摆放在一起，于是这两种商品的销量增大，为超市带来可观收益。这个小小例子足以说明数据挖掘的重要性。

数据挖掘遵循一定步骤：首先要确定业务对象，然后是数据准备工作，在数据准备工作中有数据选择、数据预处理、数据转换、数据挖掘、结果分析和知识同化这些步骤，如图1所示。

2 决策树ID3算法基本原理

2.1 信息增益与信息熵概念

信息增益和信息熵是ID3算法中最重要的两个概念，简单来说，在ID3算法中，信息增益最大的节点属性作为划分标准，信息熵是当获取信息时，将不确定的内容转为确定内容，因此信息伴着不确定性，分别有以下数学定义：

其中，Gain值越大，说明选择测试属性对分类提供的信息越多。

信息熵：已知随机样本的集合T中的样本个数为a，有n个互不相同的值为类别属性，即可得到n个类别 Mi （i=1，2，…，n）。假设Mi的样本个数为ai，则某一样本分类需要的数学期望为：

在上述公式中，pi为样本集合中Mi的概率值，可以用aia计算得出，对数底数可以为任何数，不同的取值对应了熵的不同单位，通常取2。

2.2 ID3算法实现

下面给出一个实例。表1是不同年龄、收入、性别的人群对于买车或者不买车的一个训练数据集。

对于给定的行，类标号属性为买车，计数表示年龄、收入、性别在该行上具有给定值的元组数。首先计算决策属性的熵，根据信息增益与信息熵的公式可知，设买车的人数为S1，不买车的人数为S2，P1为样本中买车的概率值，P2为样本中不买车的概率值，总人数为148，可知

S1=94，S2=54

P1=94/148，P2=54/148I（S1，S2）=I（94，54）=-P1log2P1-P2log2P2=0.9388

条件属性一共有3个，年龄、收入、性别，分别计算这3个条件属性的信息增益，以计算年龄的信息熵与信息增益为例。年龄分青年、中年、老年3个组。青年买的人数为22，所占比例为22/38，不买的人数为16，所占比例为16/38，则青年的信息熵为-0.58log20.58-0.42log20.42=0.9832。同理可得中年的信息熵为0.971，老年的信息熵为0.242。

青年所占整体人数比重为38/148=0.26，中年所占整體人数的比重为60/148=0.41，老年所占整体人数的比重为50/148=0.33。

则年龄的平均期望为：

E（年龄）=0.26*0.9832+0.41*0.971+0.33*0.242=0.7336

年龄的信息增益为：

G（年龄）=0.9388-0.7336=0.2052

同理可算出收入的信息增益为0.6628，性别的信息增益为0.3858，可知收入的信息增益是最大的，因此选择性别为决策树的根结点，如图2所示。

找到了根结点后，其它叶子结点的寻找过程与根结点的寻找过程一样。

3 决策树ID3算法的改进算法

3.1 ID3算法的不足

虽然ID3算法理解简单，使用方便，适用于处理大规模的学习问题，但是ID3算法并不适应所有的数据挖掘和机器学习问题， ID3算法效率较低。下面归纳出ID3算法的不足之处：

（1） 因为ID3算法为一种贪心算法，即在对问题求解时，总是做出目前状况下的最好选择。换句话说，在算法过程中，不从整体最优上加以考虑，算法选择只是某种意义上的局部最优解。因此，ID3算法的决策树搜索是无回溯的，很有可能在得到局部最优解后丢失了全局最优解。

（2） ID3算法只能处理离散属性，对于连续值的属性，必须首先对其进行离散化处理才能投入使用。比如年龄属性就是一个连续值属性，在ID3算法中对这种连续值属性是无法进行计算的，必须先将年龄属性离散化才能进行下一步计算。

（3） ID3的决策树计算中，每个叶子节点都必须要有属性值才能进行计算，但是并不是每个节点都必须拥有属性值，如果样本的某个属性缺少对应的属性值，那么ID3算法计算将无法继续，只能对缺省值进行赋值才能继续计算。

3.2 ID3改进算法实现

由ID3算法可知，生成決策树的关键是找到根结点，ID3算法是计算各个属性的信息熵和信息增益来寻找根结点的。下面介绍ID3算法的一种改进算法——MIND算法，通过计算各个属性的基尼系数来寻找到根结点以及叶子结点。

基尼系数或译坚尼系数，是20世纪初由意大利经济学家基尼根据劳伦斯曲线所定义的判断收入分配公平程度的指标。 基尼系数是一个比例数值，在0和1之间，是国际上用来综合考察居民内部收入分配差异状况的一个重要指标。我们可以利用基尼系数的思想来计算属性的分配程度，从而选择决策树的根结点。

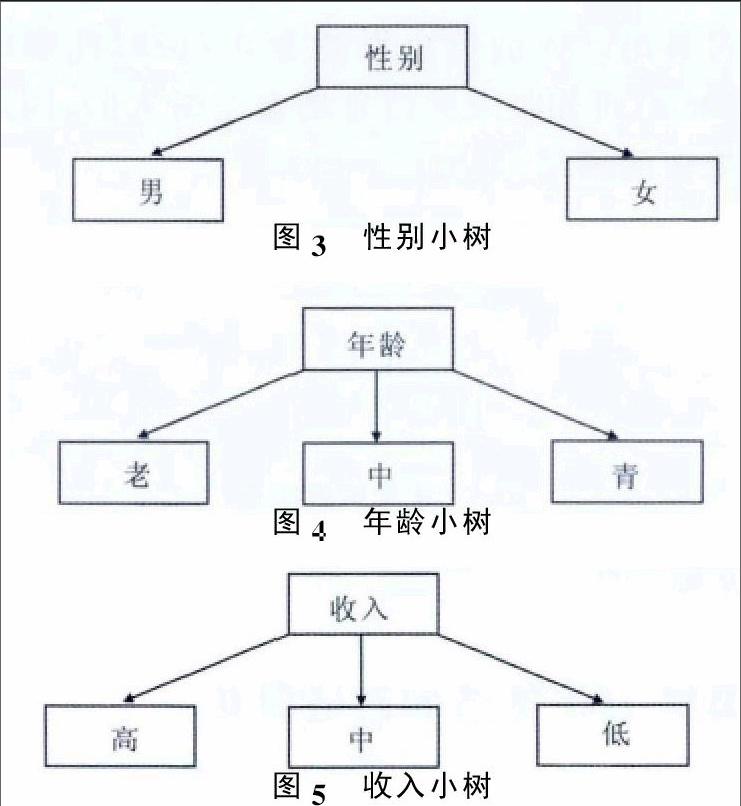
MIND算法具体操作：将各个属性按类别分成不同的小树。

因为买/不买为类标号属性，因此令S1（买）=94，S2（不买）=54。

计算年龄属性的基尼系数，已知青年中买的人数为22，不买的人数为16，因此记为青（22，16），中年中买的人数为24，不买的人数为36，因此记为中（24，36），老年中买的人数为48，不买的人数为2，因此记为老（48，2）。

Gini（青）=1-[（2238）2+（1638）2]=0.488

Gini（中）=1-[（2460）2+（3660）2]=0.48

Gini（老）=1-[（4850）2+（250）2]=0.0768

由上式可知，年龄属性的基尼系数为

Gini（年龄）=38148×0.488+60148×0.48+50148×0.0768=0.346

计算收入属性的基尼系数：已知低收入中买的人数为2，不买的人数为34，因此记为低（2，34）；中收入中买的人数为12，不买的人数为20，因此记为中（12，20）；高收入中买的人数为80，不买的人数为0，因此记为高（80，0）。计算得：Gini（低）=0.105，Gini（中）=0.469，Gini（高）=0，Gini（收入）=0.127。

计算性别属性的基尼系数：已知男性中买的人数为50，不买的人数为34，因此记为男（50，34）；女性中买的人数为44，不买的人数为20，因此记为女（44，20）。计算得：Gini（男）=0.482，Gini（女）=0.43，Gini（性别）=0.46。

由上述计算可知，收入的基尼系数是最小的，因此选择收入作为决策树的根结点，这个结论与ID3算法一样。根结点决策树与图2一致。

4 结语

本文利用一种新的MIND算法对ID3算法进行改进，从而实现寻找到决策树根结点的简便计算方法。新算法引入基尼系数概念，可以适当减少非重要属性的信息量，相应减少ID3算法对取值较多的属性依赖性，使整个运算更加独立，从而改善分类规则和结果。

参考文献：

[1]谭建豪，章兢，黄耀，等. 数据挖掘技术[M].北京：中国水利水电出版社，2009：16-148.

[2]DAVIDSON IAN，TAYI GIRI. Data preparation using data quality matrices for classification mining[J]. European Journal of Operational Research，2009， 197（2）：764-772.

[3]朱付宝，霍晓齐，徐显景. 基于粗糙集的ID3决策树算法改进[J].郑州轻工业学院学报：自然科学版，2015，30（1）：50-54.

[4]王小巍，蒋玉明.决策树ID3算法的分析与改进[J].计算机工程与设计，2011，32（9）：3070-3072.

（责任编辑：杜能钢）