介质覆盖金属光栅混合表面等离子模式光学特性研究

马良，庞天一，李京羊，施凯明，叶子凡，陈国强，周见红

（长春理工大学光电工程学院，长春 130022）

介质覆盖金属光栅混合表面等离子模式光学特性研究

马良，庞天一，李京羊，施凯明，叶子凡，陈国强，周见红

（长春理工大学光电工程学院，长春 130022）

采用时域有限差分法与耦合模理论，研究了介质覆盖金属光栅表面等离子混合模式的光学共振特性。研究结果表明，在所研究的结构中，覆盖介质支撑的混合表面模式与金属光栅所支撑的表面等离子模式相互作用引起抗交叉效应；利用耦合模理论，对此系统的反射特性进行了建模研究，得出了减小吸收的条件。此耦合系统的所有光学特性都采用了时域有限差分法进行验证，理论结果与数值模拟结果一致。

耦合模理论；时域有限差分法；金属光栅；表面等离子体模式；抗交叉效应

表面等离子激元是电磁场与金属表面传导电子相互耦合引起的传导电子集体共振的结果［1-6］。表面等离子激元的能量被限制在金属的表面传播，这种光学特性可以应用在生物医学、化学传感［7］、表面等离子激光［8］、表面增强拉曼散射［9］、光伏器件等领域［10］。表面等离子导模与表面等离子共振导模这两类模式都是由金属-介质界面支撑，表面等离子导模在金属-介质界面传播与外界电磁场不存在耦合，即没有辐射损耗；表面等离子共振导模的电磁场也是被限制在金属-介质界面传播，它能够利用光栅［11，12］、棱镜［13，14］、近场来激发［15］，不同于表面等离子导模，表面等离子共振导模能够与外界电磁场进行强烈的相互耦合。利用金属光栅结构激发表面等离子导模与表面等离子共振导模得到了广泛研究。然而，介质覆盖金属光栅结构中的混合表面等离子导模特性研究却很少。

本文中，利用时域有限差分法与耦合模理论，研究了介质覆盖金属光栅结构中共振导模的光学特性。介质薄膜所支撑的混合表面等离子模与金属光栅所支撑的表面等离子模相互作用，由于抗交叉效应两者相互混合并且交换光学特性。用耦合模理论还对系统的反射和吸收特性进行了建模研究，得到吸收减少的条件。此耦合系统的所有光学特性均被数值模拟（时域有限差分法）所验证。

1 共振模式的色散关系

图1是一个周期的光栅共振耦合系统示意图，由介质材料覆盖金属光栅组成，周围是空气，d（=642nm）是光栅周期，h2是金属光栅脊部分的介质厚度，w（=0.25d）和h1（=0.04d）分别是金属光栅脊的宽度和高度，介质材料采用介电常数为6的ZnS，忽略材料折射率对波长的依赖性。在可见光与近红外范围内，贵金属（例如银、金、铜）的光学色散特性可由Drude模型描述

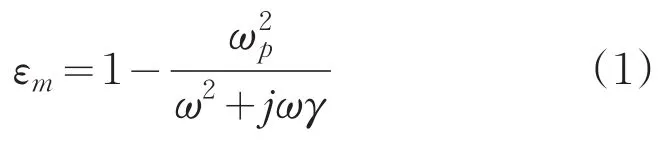
其中,ω为光的角频率，ωp为金属体材料的体等离子频率，γ是电子碰撞频率。本文采用的金属材料为银，利用此模型ωp=1.32×1016rad/s，γ=6.8× 1013rad/s［16］。

图1 单位周期介质覆盖金属光栅示意图

为了获得介质覆盖金属光栅系统的表面共振模式，用二维时域有限差分法，在单位周期结构中，左右边界采用周期边界条件，顶部和底部采用吸收边界条件进行计算［17-19］。模拟中，用高斯分布的近场TM偏振点光源进行表面等离子模式激发。图2（a）和（b）给出了h2=0.50d时，此结构简约布里渊区色散关系。图2（c）给出h2=0.45d时的色散关系，分析此结构随介质材料厚度与抗交叉效应的变化。图2（a）右下光锥以下灰色区域为表面等离子导模，主要研究光锥上方传导共振辐射模式，尤其是在布里渊区边界kxd=0处混合表面传导模式与等离子模式之间相互作用，如图2（b）所示。

图2（b）中，布里渊区边界kxd=0处，上方模式是关于镜面对称的偶模，主要由金属光栅激发，下方模式也是一个偶模，主要由介质材料激发。尽管两种模式非正交，但由于频率差异较大，他们之间的相互作用比较弱，抗交叉效应不明显。然而，中间两个模式都是奇模，在kxd=0.15附近产生抗交叉效应。由于抗交叉效应，两个模式相互混合，交换彼此之间的光学特性，在TM模式平面波垂直照射下，只有奇模可以被激发，所以在此文中，只研究这两个模式。

入射到光栅表面的光会沿光栅表面前向和后向传播，传播常数kx满足相位匹配条件［6］θ与m分别表示入射角度与衍射级次。对于θ=0o时，沿表面前后向传播的表面波形成驻波。图2中附近处混合模式与表面等离子模式的衍射级次为m=±1和m=±2，前后方传播的波分别形成驻波，如图3所示。

图2 介质覆盖金属光栅的色散关系

图3为混合模式在简约布里渊区边界处kxd=0的场分布。比较图3（a）和（c），在y方向上有一个波节，此混合共振模式由介质与空气支撑。图3（c）中沿光栅表面上的相移为4π，而介质-空气界面相位变化为2π，相比于图3（a），更多的体现出等离子模式特性，这是由于当h2=0.50d减小到h2=0.45d，两个表面等离子模式之间发生抗交叉效应，模式混合增强，从图2（b）和（c）中也可看出。对于图3（b）和（d）模式，束缚在光栅表面，更多的体现出表面等离子特性。

图3 介质覆盖金属光栅结构在简约布里渊区边界处kxd=0时的电场分布

从图3中，可以得出这样一些结论：（1）两种模式的混合主要发生在介质区域；（2）介质材料上方空气中的电场迅速衰减，一个周期的相移是2π，与表面等离子模式不同；（3）对于混合模式，电场主要分布在介质材料和空气中，而表面等离子模式电场主要分布在光栅表面；（4）混合共振模式对介质层厚度敏感性要高于表面等离子模式。

2 光学反射特性

如图1，当一束TM偏振波垂直入射到该系统，只有奇对称共振传导模式被激发。图4给出了不同介质材料厚度h2下FDTD模拟的反射率，吸收谷处为表面传导模式的共振频率。

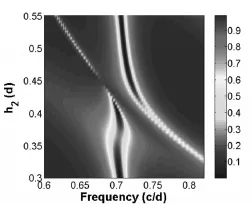
图4 介质覆盖金属光栅d=642nm，w=0.25d，h1=0.04d时随反射率随h2变化关系

从图4中可以看出，在f=0.7(c d)附近的表面等离子模式对介质的厚度不敏感，因为表面等离子模式主要由相位匹配条件［6］决定，并且该模式的能量大多被限制在介质材料中，如图4（a）和（b）所示。这种由介电材料支撑的混合共振模式，对介电材料的厚度十分敏感，增加材料厚度时，该共振模式会出现红移。表面等离子模式吸收峰比混合共振模式要宽。当介电材料厚度h2在0.45d附近时候，由抗交叉效应产生的模式混合会非常明显，如图3（c）（d）所示。当h2=0.50d时，混合共振模式（图3（a））和表面等离子模式（图3（b））的混合就不再明显了。

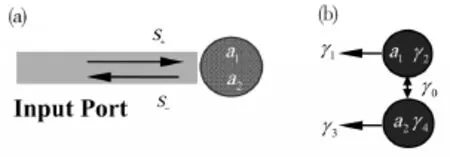
图5 单端口多模共振系统耦合示意图

需要指出的是，当h2=0.45d时，只有反射谱频率处存在吸收峰（表面等离子模式），而频率处，混合共振导模不能通过反射谱中吸收峰显示。

为了分析介质覆盖金属光栅系统中混合模式和表面等离子模式（如图1所示），通过耦合模理论来进行建模并分析两种共振导模之间的相互作用，如图5（a）所示，对于垂直入射情况，由入射波激发的两种模式归一化振幅为，其中表示入射光，因为这两个模式并不是正交的，所以它们之间存在相互耦合，如图5（b）所示。此系统的模式随时间变化关系为

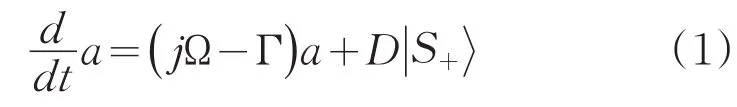
其中，Ω，Γ和D分别代表共振频率，衰减矩阵和耦合矩阵，即

当共振模式被激发，金属光栅的出射光和吸收光可表示为

其中，rd和td为实数，且r2d+t2d=1，jtd表示吸收过程，而不是传统意义上的传输过程。

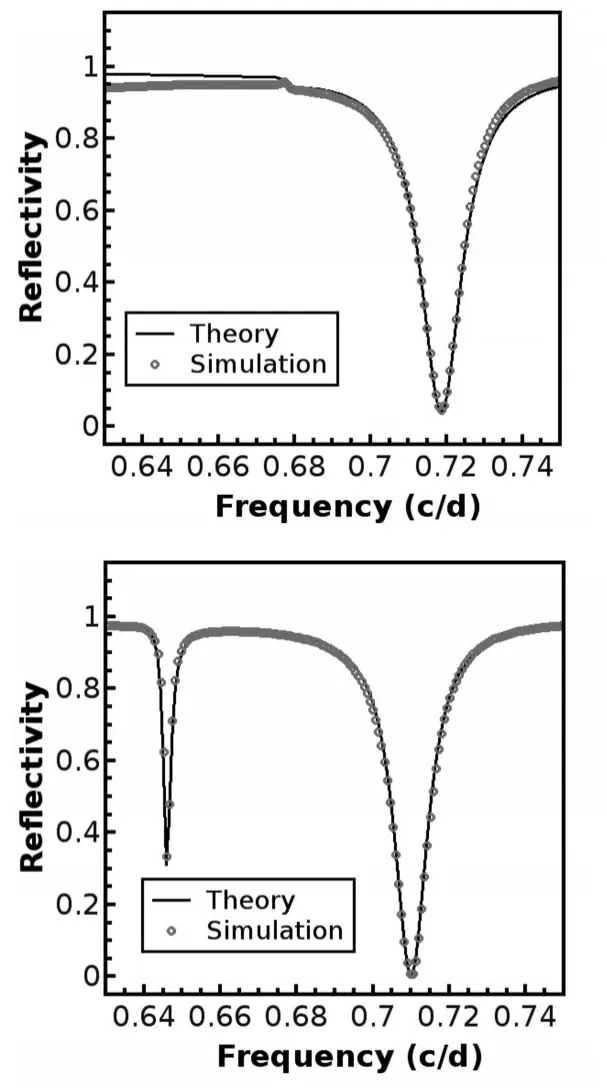
图6 介质覆盖金属光栅结构的反射率曲线

圆点是时域有限差分法模拟结果，实曲线是理论分析方程（7）得到的。（a）h2=0.45d（b）h2=0.50d；两个共振峰的理论参数（单位为

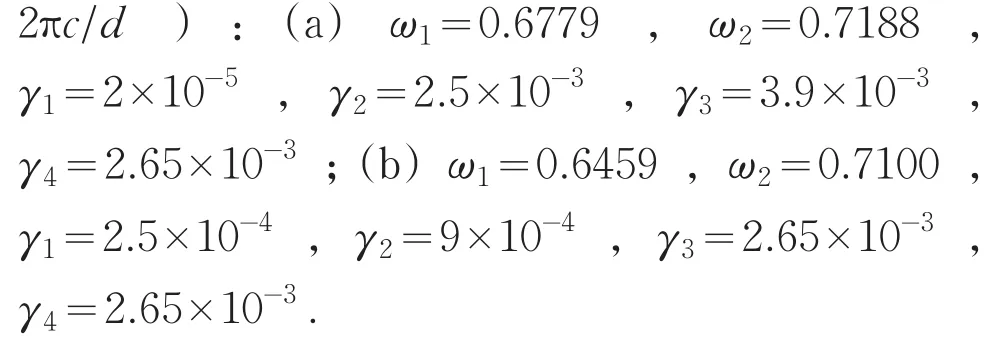
需要注意的是，在衰减矩阵Γ中，γ1（γ3）和γ2（γ4）分别表示由于出射光波和吸收所引起的模式振幅a1（a2）衰减，γ0表示图5（b）中两种模式之间的相互耦合系数，由能量守恒，耦合矩阵元素之间有关系［21，22］

耦合矩阵D和散射矩阵C它们之间存存在相互限制，

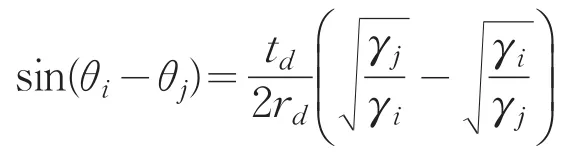
由式（4）得，每个模式由反射和吸收所造成的衰减速率也存在限制

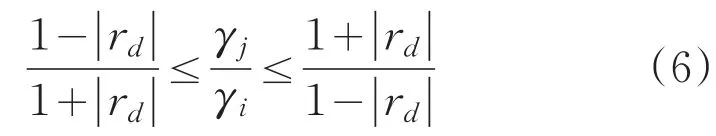
由式（1）和（2）得到系统反射系数的表达式为

以上理论推导适用于任何非正交模式的光学共振耦合系统，为了解释介质覆盖金属光栅系统的反射特性，将FDTD模拟结果与理论分析相对比，其中h2=0.45d和h2=0.50d分别如图6（a）和（b）所示。实线为理论分析结果，离散点为FDTD模拟结果，图6（a）中，在处共振吸收谷消失。由式（7），发现当时，共振吸收谷消失，同时注意到，当γ3=γ4时，共振吸收谷趋近于0，如图6（b）中处所示。FDTD验证了耦合模理论分析结果的正确性。

3 结论

采用时域有限差分法与偶合模理论研究了介质覆盖金属光栅系统中混合表面模式和表面等离子模式的光学特性，通过时域偶合模理论进行建模，并采用时域有限差分法研究了色散特性、抗交叉效应以及反射特性，理论研究与数值模拟结果一致。

［1］Britt Lassiter J，Sobhani H，Fan A F，et al.Fano resonance in plasmonic nanoclusters：geometrical and chemical tunability［J］.Nano Lett.，2010（10）：3184-3189.

［2］Balci S，Kocabas C.Ultra hybrid plasmonics：strong coupling of plexcitons with plasmon polaritons［J］. Opt.Lett.，2015（40）：3424-3427.

［3］Gallinet B，Martin O J F.Influence of electromagnetic interactions on the line shape of plasmonic fano resonances［J］.ACS Nano，2011（5）：8999-9008.

［4］Dregely D，Hentschel M，Giessen H.Excitation and tuning of higher-order fano resonances in plasmonic oligomer clusters［J］.ACS Nano，2011（5）：8202-8211.

［5］Leong H，Guo J.Surface plasmon resonance in superperiodic metal nanoslits［J］.Opt.Lett.，2011（36）：4764-4766.

［6］Mishima Y，Habara H，Tanaka K A.Two plasmonic mode excitation using a double-step rectangle grating［J］.J.Opt.Soc.Am.B，2015（32）：1804-1808.

［7］Tawa K，Hori H，Kintaka K，et al.Optical microscopicobservationoffluorescenceenhancedbygrating-coupled surface plasmon resonance［J］.Opti.Expr.，2008（16）：9781-9790.

［8］Okamoto T，Simonen J，Kawata S.Plasmonic band gaps of structured metallic thin films evaluated for a surface plasmon laser using the coupled-wave approach［J］.Phys.Rev.B，2008（77）：115425.

［9］MandalP，Nandi1A，RamakrishnaS.Propagating surface plasmon resonances in two-dimensional patterned gold-grating templates and surface enhanced Ramanscattering［J］.J.Appl.Phys，2012（112）：044314.

［10］Lu D，Rengnath E，Cui Y，et al.Interaction of two plasmon modes in the organic photovoltaic devices with patterned back-electrode［J］.Appl.Phys.Lett，2013（102）：241114.

［11］Park S，Lee G，Song S，et al.Resonant coupling of surface plasmons to radiation modes by use of dielectric gratings［J］.Appl.Phys.Lett，2003（28）：1870-1872.

［12］Devaux E，Ebbesen T，Weeber J，et al.Launching and decoupling surface plasmons via micro-gratings［J］.Appl.Phys.Lett，2003（83）：4936-4939.

［13］Raether H.Surface plasmons［M］.New York：Springer-Verlag，1988.

［14］QuailM，RakoJ，SimonH.Long-rangesurface wave-plasmon modes in silver and aluminum films［J］.Opt.Lett.，1983（8）：377-379.

［15］Hecht B，Bielefeld H，Novotny L，et al.Local excitations scattering，and interference of surface plasmons［J］.Phys Rev.Lett.，1996（77）：1889-1892.

［16］Chiu R，Lan Y，Chen C.Plasmonic Bloch oscillations in cylindrical metal-dielectric waveguide arrays［J］.Optics Letters，2010（35）：4012-4014.

［17］Oskooi A，Johnson S G.Distinguishing correct from incorrect PML proposals and a corrected unsplit PML for anisotropic，dispersive media［J］.Journal of Computational Physics，2011（230）：2369-2377.

［18］Taflove A，Hagness S C.Computational electrodynamics：thefinite-differencetime-domainmethod［M］.Artech House，Norwood，Mass.，2000.

［19］Farjadpour A，Roundy D，Rodriguez A.Improving accuracy by subpixel smoothing in FDTD［J］.Opt. Lett，2006（31）：2972-2977.

［20］Haus H A.Waves and fields in optoelectronics［M］. Prentice-Hall，Englewood Cliffs，N.J.，1984.

［21］Suh W，Wang Z，Fan S.Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multi-mode cavities［J］.IEEE Journal of Quantum Electronics，2004（40）：1511-1518.

［22］Zhou Jianhong，Meng Ying，Song Hongfei，et al.“Transfer matrix”method for direct and indirect coupling of cascaded cavities in resonator-waveguide systems［J］.Opt.Comm.，2014（329）：88-94.

Hybrid Surface Plasmonic Guided Resonance in a System with Dielectric Covered Metallic Grating

MA Liang，PANG Tianyi，LI Jingyang，SHI Kaiming，YE Zifan，CHEN Guoqiang，ZHOU Jianhong
（School of Optoelectronic Engineering，Changchun University of Science and Technology，Changchun 130022）

The optical properties of resonant guided modes in a system with metallic grating covered by dielectric material are investigated by the finite-difference time-domain method and coupled-mode theory.Two kinds of guided resonant modes，the hybrid surface modes supported by the dielectric material and plasmonic surface modes supported by the metallic grating，are mutually coupling and mixing due to anti-crossing.The optical reflective properties of the system are also modeled and investigated by the coupled-mode theory.Conditions for the absorption reduction are also obtained.All the characteristics of the coupling systems are confirmed numerically by the finite-difference time-domain method.

coupled-mode theory；finite-difference time-domain method；metallic grating；surface plasmonic mode；anti-crossing

O436

A

1672-9870（2017）01-0076-05

2016-10-24

国家自然科学基金资助（11474041）

马良（1991-），男，硕士研究生，E-mail：1534888268@qq.com