基于权重为区间数的区间直觉模糊多属性决策

张亚丰，潘小东

(西南交通大学 数学学院，四川 成都 610031)

基于权重为区间数的区间直觉模糊多属性决策

张亚丰，潘小东

(西南交通大学 数学学院，四川 成都 610031)

针对属性权重为区间数和属性值为区间值直觉模糊集的多属性决策问题，提出了一种新的基于理想解的决策方法。首先，定义了两个区间直觉模糊集的距离、属性权重与属性值之间的运算及正负理想方案；其次计算各个备选方案到理想方案的距离，通过评价指数公式判断方案的优劣；最后，通过一个具体的实例说明该方法的可行性。

区间值直觉模糊集；理想解；多属性决策

在考虑多个属性或指标的情况下，选择最佳备选方案或排序有限备选方案的决策问题称为多属性决策。由于客观事物的复杂性，在实际问题中，我们面临的多数多属性决策问题都是在目标、约束以及一系列行动等没有明确规定的环境下进行的。若决策的目标、约束或权重等要素是通过模糊谓词来描述的，这样的决策问题称为模糊多属性决策。1965年，美国加利福尼亚大学ZadehLA教授[1]提出了模糊集合的概念，在此之后，模糊多属性决策的理论和方法得到了迅速的发展。由于其在人工智能、经济、管理和工程等[2-3]诸多领域的广泛应用，关于模糊多属性决策问题的研究越来越受到研究者的重视。

在经典的多属性决策问题中，人们常常利用TOPSIS(TechniqueforOrderPreferencebySimilaritytoanIdealSolution)方法从备选方案中寻找最优方案，由此建立了一些非常有效的决策方法。自然地，人们也希望能够将TOPSIS方法应用到模糊多属性决策问题中。谭吉玉等[4]提出了基于TOPSIS的区间数相对贴近度法。该方法无需建立可能度矩阵，可根据相对贴近度大小直接排序；该方法研究权重和属性均为区间数的决策问题，却又将区间数权重转化为实数权重，没有实质意义。屈文阁[5]为了减少决策信息的损失，将区间数权重直接参与运算。然而，定义的正负理想方案会随方案的增加而改变，从而导致方案增加时，原有方案排序出现逆序问题。周晓辉等[6]定义了Hamming距离，它表示具有多种因素的两事物的靠近程度，综合考虑了事物的属性差异，比欧氏距离优越。但是对每个方案的属性进行了两次加权运算，使得方案的综合评价值无明显差异。谭春桥[7]定义了区间直觉模糊集之间的欧氏距离，根据TOPSIS方法的原理，对方案进行排序。然而计算每个方案到正(负)理想方案的距离，却取其上下界的平均值，这是不合理的。付亚男等[8]结合TOPSIS方法定义了相对贴近度及总贴近度公式,解决了权重完全未知的区间直觉梯形模糊多属性决策问题，但其没有考虑直觉模糊集中不确定性对决策结果的影响。

本文针对属性权重为区间数和属性值为区间值直觉模糊集的多属性决策问题，综合考虑直觉模糊集的隶属度、非隶属度及犹豫度3方面对决策结果的影响，新定义了区间直觉模糊集的Hamming距离。还定义了正负理想方案，使其不会因为方案的增加而导致原有方案的排序出现逆序问题。

1 预备知识

对于X上每一个直觉模糊集，称πA(x)=1-μA(x)-vA(x)为直觉模糊集A中元素x属于A的犹豫度。例如(μA(x),νA(x))=(0.6,0.3)，在投票模型中可理解为在10人中，有6人赞成、3人反对、1人弃权。由于客观事物的复杂性和不确定性，μA(x)和νA(x)的值往往难以用精确的数值来表示，而用区间数比较合适，因此Atanassov[10]对直觉模糊集进行了拓展，提出了区间直觉模糊集。

对于X上的每一个区间值直觉模糊集，下述函数表示区间直觉模糊集A中元素x属于A的不确定度，即犹豫度：

为了充分利用区间信息，使区间与区间直觉模糊集之间的信息能够更好地融合，根据文献[2]对区间与区间直觉模糊集有如下定义：

a⊗b =[m,n]⊗([μL,μU],[νL,νU],[πL,πU])]

=([mμL,nμU],[mνL,nνU],[mπL,nπU])。

(1)

为了刻画区间直觉模糊集之间的差异程度，下面给出了区间直觉模糊集之间的距离。

定义1.4 设非空经典集合X={x1,…,xn},

A、B是定义在X上的两个区间直觉模糊集，令

(2)

(3)

A、B之间的距离为

(4)

其中：λ为分辨系数，一般取λ=0.5。

上述距离刻画直觉模糊集之间的差异性，当上界距离与下界距离均越小时，A、B之间越接近，故一般取上下界的平均值。在一般的理想解的多属性决策问题中 ，每个方案属性取具体的数值，因此，到理想解的距离是具体的数值。然而，当方案属性取值为区间时，到理想解的距离也形成了一个区间，我们引入变化的λ，可以看到每个方案属性值取区间中的每个值时的不同情况(在对所有方案没有任何偏好的情况下)。

2 基于区间直觉模糊集的多属性决策模型

根据定义1.3和定义1.4，下面建立属性权重为区间数、属性值为区间直觉模糊值的理想解决策模型，具体步骤如下：

2.1 建立区间值直觉模糊决策矩阵

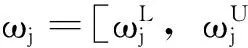
2.2 构造加权规范化决策矩阵

由于属性值由区间直觉模糊值给出，无需进行规范化，根据式(1)得加权规范化矩阵为：

2.3 确定正理想方案和负理想方案

负理想解为：

2.4 确定各备选方案到正负理想方案的距离

备选方案到正理想方案的距离越小，那么到负理想方案的距离就会越大，备选方案就会越优。因此，给出下式：

(5)

(6)

2.5 计算备选方案ai的综合评价指数

(7)

此综合评价指数表示各备选方案ai与正理想方案A+和负理想方案A-的距离进行比较，距离正理想方案越近、离负理想方案越远的备选方案的评价指数值越大。于是，按评价指数Ki从大到小对方案进行排序，Ki越大，对应方案就越优。

由于属性值取值为区间形式，因此到理想解的距离也会形成一个区间。本文引入λ，当λ越大时，决策者越乐观，希望每个方案都取区间中越好的数值，由此可以分析各个方案在不同距离下的优劣。

3 实例分析

考虑空调系统的选择问题，假设有4个空调系统构成的备选方案a1,a2,a3,a4，根据空调系统的质量c1、经济性c2和售后服务c33个指标对其进行评价。方案的属性权重为：

每个备选方案的指标评价值用下列矩阵表示：

由式(1)得加权规范化决策矩阵为：

根据式(2)、式(3)计算各方案到正负理想方案距离的上下界,得到如表1的结果。

表1 各方案到正负理想方案距离的上下界

根据式(4)、式(5)、式(6)计算各方案在不同分辨系数下的评价指数，结果如表2所示。

表2 各方案在不同分辨系数下的评价指数

从表2可以看出，在不同分辨系数λ下，各方案的排序结果均为A4>A2>A3>A1，并没有随分辨系数λ的变化而变化，说明该方法的可行性，故方案A4为最佳方案。

运用文献[11]的决策方法，计算的排序结果为A2>A4>A3>A1。与文献[11]相比，由于权重的不确定性，本文取属性权重为区间数，相对于文献[11]权重为实数更加具有说服力，减少了决策信息的损失，决策结果也更加符合现实生活。定义了Hamming距离，提高了运算效率，同时引入了辨系数λ，可以看到各方案在不同分辨系数下优劣程度(即各方案属性值取区间直觉模糊值中越大值，方案会越来越优)。

4 结 语

针对属性权重为区间数和属性值为区间直觉模糊值的决策问题，定义了权重与属性值之间的运算法则和区间直觉模糊集之间的距离公式，提出了一种新的理想解决策理论模型。该方法提高了运算效率，处理的决策结果更加符合现实生活，最后通过具体的实例说明该方法的有效性。

[1]ZadehLA.Fuzzysets[J].InformationandControl,1965(8):338-356.

[2] 徐泽水.不确定多属性决策方法及其应用[M].北京：清华大学出版社，2004:41-45.

[3] 卫贵武.基于模糊信息的多属性决策理论与方法[M].北京：中国经济出版社，2010:36-38.

[4] 谭吉玉，朱传喜，张小芝，等.一种新的基于TOPSIS的区间数排序法[J].统计与决策，2015(1):94-96.

[5] 屈文阁.一种区间数多属性决策方法在经济评价中的应用[J].甘肃科学学报，2013，25(4):152-155.

[6] 周晓辉，姚俭，吴天魁.基于梯形直觉模糊数的TOPSIS多属性决策方法[J].控制与决策，上海理工大学学报，2014,36(3):281-286.

[7] 谭春桥.基于区间值直觉模糊集的TOPSIS多属性决策[J].模糊系统与数学，2010,24(1):92-97.

[8] 付亚男,毛军军,徐丹青.基于区间直觉梯形模糊数的改进TOPSIS多属性决策方法[J].数学的实践与认识，2014,44(17):134-140.

[9]AtanassovK.Intuitionisticfuzzysets[J].FuzzySetsandSystems，1986，20：87-96.

[10]AtanassovK,GargovG.Interval-valuedintuitionisticfuzzysets[J].FuzzySetsandSystems，1989，31(3)：343-349.

[11] 谭吉玉,朱传喜.基于TOPSIS的区间直觉模糊数排序法[J].控制与决策，2015,30(11):2014-2018.

Interval-valued Intuitionistic Fuzzy Multiple Attribute Decision Making Based on Interval Number Weight

ZHANGYafeng,PANXiaodong

(SouthwestJiaotongUniversity,Chengdu610031,China)

Aimingatmultipleattributedecisionmakingproblemsofinterval-valuedintuitionisticfuzzyset,wheretheattributeweightsareintervalnumbersandtheattributevaluesareintervalvalues,thispaperproposesanewdecisionmethodbasedontheidealsolution.Firstly,thedistanceoftwointervalintuitionisticfuzzysets,theoperationbetweenattributeweightsandattributevaluesandthepositiveandnegativeidealalternativearedefined.Then,thedistanceofeveryalternativetothepositiveidealalternativeandthenegativeidealalternativearecalculated.Thealternativescanbeevaluatedthroughthejudgmentindexformula.Finally,thispaperillustratesthefeasibilityofthismethodwithaconcreteexample.

intervalintuitionisticfuzzysets;theidealsolution;multipleattributedecisionmaking

2016-09-06

张亚丰(1989-)，男，河南济源人，在读硕士研究生，主要从事模糊数学方面的研究.

10.3969/i.issn.1674-5403.2017.01.023

O

A

1674-5403(2017)01-0089-05