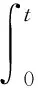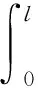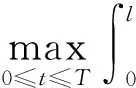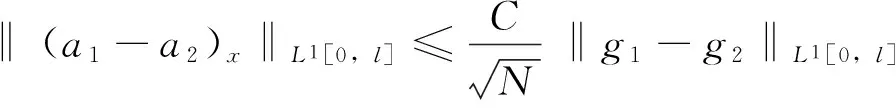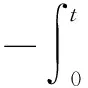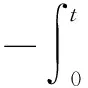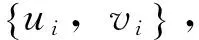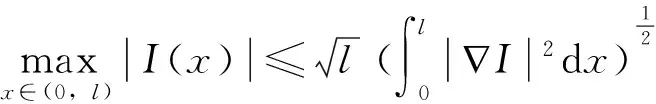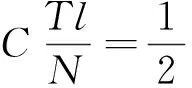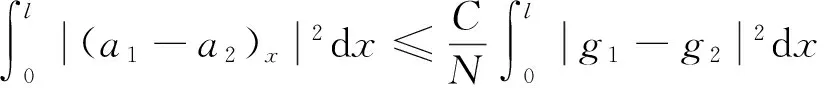关于一类热传导方程的间断扩散系数的稳定方法

曾 剑,刘 云,甄苇苇

(兰州交通大学 数理学院,甘肃 兰州 730070)

关于一类热传导方程的间断扩散系数的稳定方法

曾 剑,刘 云,甄苇苇

(兰州交通大学 数理学院,甘肃 兰州 730070)

考虑了一类利用终端观测值反演热传导方程中间断扩散系数的反问题, 此类问题无论是在理论讨论还是在实际应用中都有极其重要的研究意义。相较于扩散系数连续的文献, 间断的情形鲜有文献涉足,由于控制泛函非凸,一般来说没有唯一性,在假设T比较小的情况下,证明了极小元的唯一性和稳定性。

热传导方程;间断扩散系数;非凸;稳定性;唯一性

通常扩散系数可作为表征扩散的一个参量，它不仅与扩散机构也与扩散介质和外部条件有关。在许多实际问题中,扩散物质可以在多种介质中传播,扩散系数在介质交界面处是不连续的。

本文考虑一类特殊的扩散系数的反问题,这里的扩散系数可能是间断的。具体的数学模型如下:

(1)

其中：f和φ是两个给定的光滑函数且满足如下条件

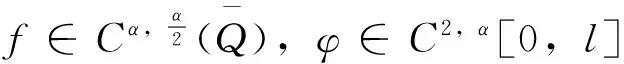
(2)

在a>0的情况下,假设φ(x)一致满足齐次Neumann边界条件。

函数a(x)在x=ε上有第一类间断点,即a(ε+0)=a(ε-0)。在间断线上满足如下的联结条件

(3)

假设给定如下的附加条件：

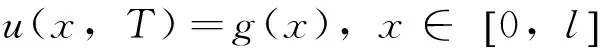
(4)

其中：g(x)是一个已知函数。利用条件(1)/条件(4)来同时确定u和a。

鉴于不适定问题的研究是偏微分方程的一个重要分支[1-2]。许多学者针对类似于条件(1)/条件(3)的问题求解做了大量的研究工作[3-8],该问题的难度在于扩散系数的不连续和问题的不适定。文献[3-4]中作者运用最优控制理论框架反演了方程ut-a(x)uxx+b(x)ux+c(x)u=f(x,t),(x,t)∈Q中的首项系数a(x)。而对于反演方程中源项f=f(x)的情况可参见文献[5]。文献[6]利用观测数据从数值计算的角度对抛物型方程中未知源项的反演问题做了研究。文献[8]研究了一类时间分数阶扩散方程的源项反演问题。

目前,国内外对一般抛物型方程的系数反演问题的研究成果已经很多[3-8],但是对抛物型方程的间断系数识别问题还很少。主要难点在于问题的强不适定性(定解数据的微小变化将导致解的巨大变化),完全非线性性(尽管本文的方程是线性的,但反问题是完全非线性的)以及系数的间断性。由于附加数据偏少,很难得到最优解的唯一性。本文利用Tikhonov正则化方法,在优化理论的基础上将一个强不适定问题转化为一个适定问题,然后证明了极小元的存在性、唯一性和稳定性。

1 最优化问题

由于问题是严重不适定的,故将原系数反演问题转化为如下的一个优化控制问题。

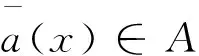
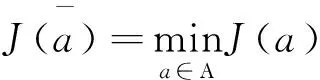
(5)

其中

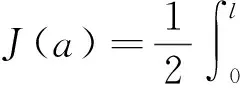
(6)

(7)

u(x,t;a)是对应于任意给定的系数a(x)∈Α,方程(1)的解;N是正则化参数,α、β是两个给定的正数。

首先,对正问题做一些讨论。

(8)

引理1.1[9]当u(x,t)是方程(8)的解且a(x)∈A是一个给定的函数时,对u(x,t)有如下的估计:

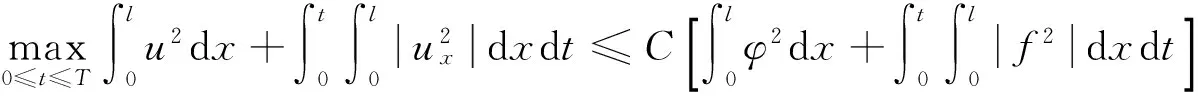
其中C是常数。

另外,要求观测数据g(x)满足

g(x)∈L2(0,l)。

(9)

显然,由条件(9)及引理1.1可知,对任意的a∈A,控制泛函(6)是适定的。

2 存在性

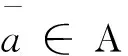
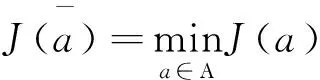
3 必要条件

定理3.1 令a是最优控制问题(5)的极小元,则存在三元函数组(u,v;a)满足下面条件：

(10)

(11)

且

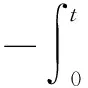
(12)

对任意h∈A都成立。

4 局部唯一性与稳定性

由于最优控制问题P1是非凸的,一般地,无法得到它的唯一解。但是,在本节中证明了当T相对较小时,极小元具有局部唯一性和局部稳定性。

引理4.1[9]对方程(10)有如下估计式:

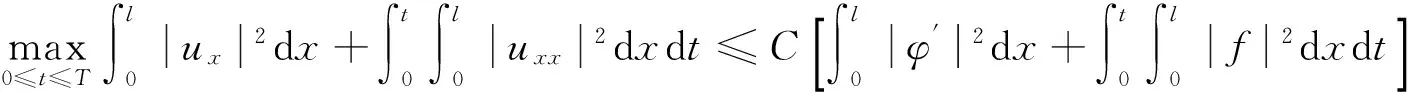
引理4.2[9]对方程(11)有如下估计式:

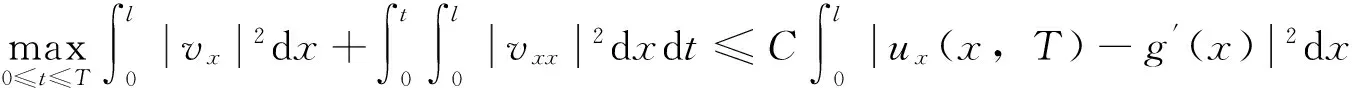
引理4.3[7]对任意有界连续函数k(x)∈C(0,l),有

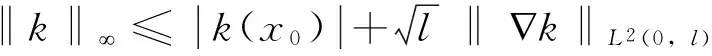
其中x0是(0,l)中的一个固定点。

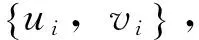
令u1-u2=U,v1-v2=V,a1-a2=I。则U和V满足

(13)

(14)

引理4.4 对方程(13)有如下的估计式成立：

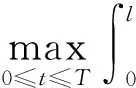
(15)

这里C与T无关。

证明: 由方程(13),当0

(16)

分部积分,得到

(17)

即

(18)

这里用到了联结条件和边界条件。

由Gronwall不等式及式(18),得到

引理4.4证毕。

引理4.5 对方程(14)有如下估计式

(19)

这里C与T无关。

(引理4.5的证明与引理4.4的证明过程类似,此处略。)

证明:在式(12)中,当a=a1时取h=a2,而当a=a2时取h=a1,于是有

(20)

(21)

由式(20)及式(21)可得

(22)

由定理的假设知存在一点x0∈(0,l)使得

I(x0)=a1(x0)-a2(x0)=0。

(23)

由引理4.3及式(23)有

(24)

由式(22)、式(24)及cauchy不等式,并利用估计式(15)和式(19),有

由引理4.1和引理4.2得

(26)

由式(23)～式(26)有

(27)

选择T<<1使得

(28)

联立式(27)和式(28)可得

定理4.1证毕。

[1] 姜礼尚,陈亚浙.数学物理方程讲义[M].3版.北京:高等教育出版社,2006:108-158.

[2] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005:51-55.

[3]JiangLS,ChenQH,WangLJ.Anewwell-posedalgorithmtorecoverimpliedlocalvolatility[J].QuantitativeFinance,2003,3(6):451-457.

[4]JiangLS,TaoYS.Identifyingthevolatilityofunderlyingassetsfromoptionprices[J].InverseProblems,2001,17(1):137-155.

[5]YangL,DengZC,YuJN.Optimizationmethodfortheinverseproblemofreconstructingthesourceterminaparabolicequation[J].MathComputSimul,2009,80(2):314-326.

[6]YangL,DehghanM,YuJN.Inverseprobemoftime-dependentheatsourcesnumericalreconstruction[J].MathComputSimul,2011,81(8):1656-1672.

[7]DengZC,YangL.Aninverseproblemofidentifyingtheradiativecoefficientinadegenerateparabolicequation[J].ChineseAnnalsMath,2014,35B(3):355-382.

[8]YangF,FuCL.Amollificationregularizationmethodfortheinversespatial-dependentheatsourceproblem[J].JComputApplMath,2014,255(2):555-567.

[9]FriedmanA.PartialDifferentialEquationsofParabolicType[M].NewJersey:Prentice-Hall,1964:11-26.

Stable Method for Discontinuous Diffusion Coefficient in Class of Heat Conduction Equations

ZENGJian,LIUYun,ZHENWeiwei

(LanzhouJiaotongUniversity,LanZhou730070,China)

Thispaperstudiesaninverseproblemofidentifyingthediscontinuousdiffusioncoefficientinaclassofheatconductionequationsfromthefinalobservation,whichisofgreatsignificancebothintheoryandpractice.Beingdifferentfromordinarycontinuousdiffusioncoefficientproblems,documentsconcernedthediscontinuouscaseareratherfew.Sincethecontrolfunctionalisnon-convex,theuniquenessoftheoptimalsolutioncannotbeguaranteed.AssumingthatTisrelativelysmall,itisprovedthattheminizerisuniqueandstable.

heatconductionequations;discontinuousdiffusioncoefficient;non-convex;stability;uniqueness

2016-11-01

曾剑(1991-),男,贵州毕节人,在读硕士研究生,主要从事数学物理反问题方面的研究.

国家自然科学基金(11461039)

10.3969/i.issn.1674-5403.2017.01.021

O

A

1674-5403(2017)01-0080-04