基于HHT和神经网络的汽车发动机故障诊断
2017-03-30韩博
韩 博
(1.兰州大学 信息科学与工程学院电路与系统研究所,兰州 730000; 2.69019部队,乌鲁木齐 830017)
● 车辆工程 Vehicle Engineering
基于HHT和神经网络的汽车发动机故障诊断
韩 博1,2
(1.兰州大学 信息科学与工程学院电路与系统研究所,兰州 730000; 2.69019部队,乌鲁木齐 830017)
针对基于汽车发动机振动信号处理的故障诊断问题,首先,利用截断矩阵奇异值分解方法对采集信号进行降噪预处理,以获取较为纯净的振动信号;然后,通过希尔伯特-黄变换(HHT)信号处理理论对采集信号进行分解与时频分析,提取出分量信号能量特征与边际谱区域变化特征两种参数作为汽车发动机故障诊断与识别的依据,并对比分析不同故障状态下的特征融和结果;最后,使用径向基(RBF)神经网络对故障样本特征进行训练,并进行多种实测故障数据的训练与识别。实际故障数据处理结果表明,上述特征参数可有效表征故障信号的时频域变化特点,可以作为汽车发动机故障的诊断依据。
故障诊断;汽车发动机;希尔伯特-黄变换;RBF神经网络
汽车发动机在运行时产生的振动信号包含重要的故障信息特征,可以反映出发动机内在各部件的健康状态。通过采集与处理汽车发动机振动信号来进行故障诊断或预测是一种常用的方法。传统的发动机振动信号分析方法是基于傅里叶变换的频域分析方法。由于发动机振动信号是一种非平稳带噪信号,傅里叶变换仅适用平稳信号的分析与处理;因此,基于傅里叶变换的算法仅能对振动信号作近似处理,限制了故障特征分析的精度与准确性。
希尔伯特-黄变换(hilbert-huang transform, HHT)信号处理理论是由美籍华人Norden E.Huang于1998年创立。该理论通过经验模态分解(empirical mode decomposition,EMD)实现信号的自适应分解处理,可以精确地分析信号在时频域的变化特征,在非平稳信号处理方面取得了良好的应用效果。王醇涛等[1]利用HHT边际谱实现了柴油机故障诊断,但没有考虑边际谱变化的区域性特征,仅利用了谱峰值作为特征参数;宋越等[2]利用HHT对发动机振动信号进行处理,成功实现了发动机气门间隙故障的诊断,但没有考虑振动信号采集中的噪声对HHT算法处理的影响。
本文依据汽车发动机振动信号的加性噪声模型,使用奇异值分解方法实现了振动采集信号的降噪预处理,有效提高了振动信号的信噪比。之后通过HHT处理方法对汽车发动机振动信号进行处理分析,依据故障信号的实际变化特性,提取出了分量信号能量特征与边际谱区域变化特征两种参数,并分析不同故障状态下的特征融和结果。最后使用径向基(radial basis function, RBF)神经网络对故障样本特征进行训练,并进行了多种实测故障数据识别,验证了本文提出算法的有效性。
1 振动信号降噪预处理
汽车发动机工作环境复杂,且由于发动机内部产生的各种激励信号经过传递或耦合都导致发动机表面的振动产生,因此在振动测量与采集过程中将产生大量的噪声信号,降低了故障特征分析与参数提取的准确性。汽车发动机振动采集信号x(k)可表示为
x(k)=s(k)+e(k)
(1)
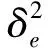
将采集到的汽车发动机振动信号序列X=(x(1),x(2),…,x(N)),利用每n点振动信号组成矩阵数据行,可构成m行n列截断矩阵形式的振动信号矩阵(N≥mn)A:
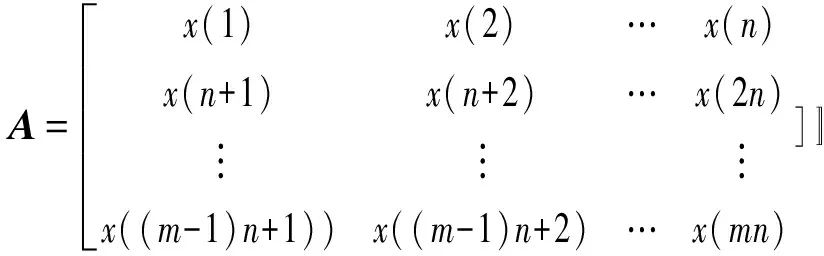
(2)
利用奇异值分解算法(SVD)可得
(3)
式中:U为m×m阶酉矩阵,U=[u1,u2,…,um];S=[diag(σ1,σ2,…,σr):O],σ1≥σ2≥…≥σr≥0为振动信号矩阵A的奇异值序列,其中r=min(m,n),O为全零矩阵;V为n×n阶酉矩阵,V=[v1,v2,…,vn]。
由奇异值分解理论可知,U与V为正交矩阵,即ui与vi各自两两正交。因此通过奇异值分解,原振动信号序列X被分解为r个相互正交的分量信号Xi:
(4)
文献[3]研究表明,截断矩阵奇异值分解具有一定的奇异值能量聚集特性。因此通过比较相邻奇异值之间变化幅度大小,即可准确估计出振动信号子空间维数值。定义Q(i)为振动信号矩阵的相邻奇异值变化量,即
Q(i)=σi/σi+1i=1,2,…,r-1
(5)

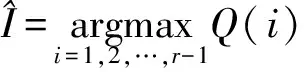
(6)
若得到振动信号子空间维数I的估计值,即可得抑制噪声后的发动机振动信号分量S与噪声分量E分别为
(7)
2 基于HHT的特征参数提取
HHT由一个独特的角度对信号成分的构成进行解释,从基础理论上突破了傅里叶变换处理的限制。其核心算法是利用EMD获取构成信号的本征模态函数(intrinsic mode function, IMF),从而实现对非平稳信号较为精确的时频分析。
2.1 故障信号EMD算法原理
实现发动机振动信号HHT,须先将振动信号进行EMD,以获取一系列瞬时频率有物理意义的单分量子信号即IMF,以令该分量信号保持瞬时频率随时间变化的单值性,从而进行Hilbert变换实现信号瞬时性质分析[4]。其中,IMF必须满足以下两个条件:一是IMF的所有极值点与过零点数量须相同或最多相差一点;二是IMF的上下包络关于时间轴对称。EMD过程简述如下:
(1)计算原信号序列的极值点,利用三次样条插值函数将所有极大值与极小值点进行包络,分别形成x(k)上下包络线;
(2)得到上下包络线的平均值m1,计算得到h1=x(k)-m1;
(3)验证h1是否满足IMF两个条件,若满足,则h1即为第一个IMF;否则将h1作为新的信号序列重复(1)(2)计算步骤,直到抽取的结果满足IMF两个条件为止,最终得到IMF信号c1;
(4)计算抽取IMF后的剩余信号:r1=x(k)-c1,然后以r1作为新的原始信号重复步骤(1)—(3),获取下一个IMF信号c2,重复n次,直到rn满足给定的终止条件(通常使rn为一单调函数)时,循环结束。此时原始信号x(k)可表示为
(8)
由此可知,EMD即是以时间特征尺度逐步将信号的局部模态分离,将复杂的非平稳信号分解为一系列单分量信号的和。而每个IMF信号都反映出不同的信号成分,表示信号的内在模态特征,同时可能显示出频率成分来源,方便对故障原因进行分析。相比于傅里叶变换,EMD无固定基函数,因此具有自适应分解特性[5]。以汽车发动机内环故障振动信号为例进行EMD得到12个IMF信号分量,结果如图1所示。

图1 汽车发动机内环故障振动信号EMD结果
2.2 故障信号的HHT时频分析
通过EMD分解得到一系列IMF信号分量,若对每个IMF分量进行Hilbert变换可得到具有实际意义的瞬时频率和瞬时幅值。将所有IMF分量的Hilbert变换结果进行组合可得到信号的HHT时频谱 ,包含了信号的瞬时频率、时间与能量的变化情况。图2所示为汽车发动机内环故障振动信号的HHT时频谱。由时频谱可以清晰地看出故障信号的频率变化轨迹,以及信号能量在不同频率范围内的变化形态。故障信号的瞬时频率源于故障因素造成的频率发生源,因此由HHT时频谱即可得到准确的瞬时频率变化形态,并可据此分析故障源。

图2 汽车发动机内环故障振动信号HHT时频谱
2.3 故障信号特征提取
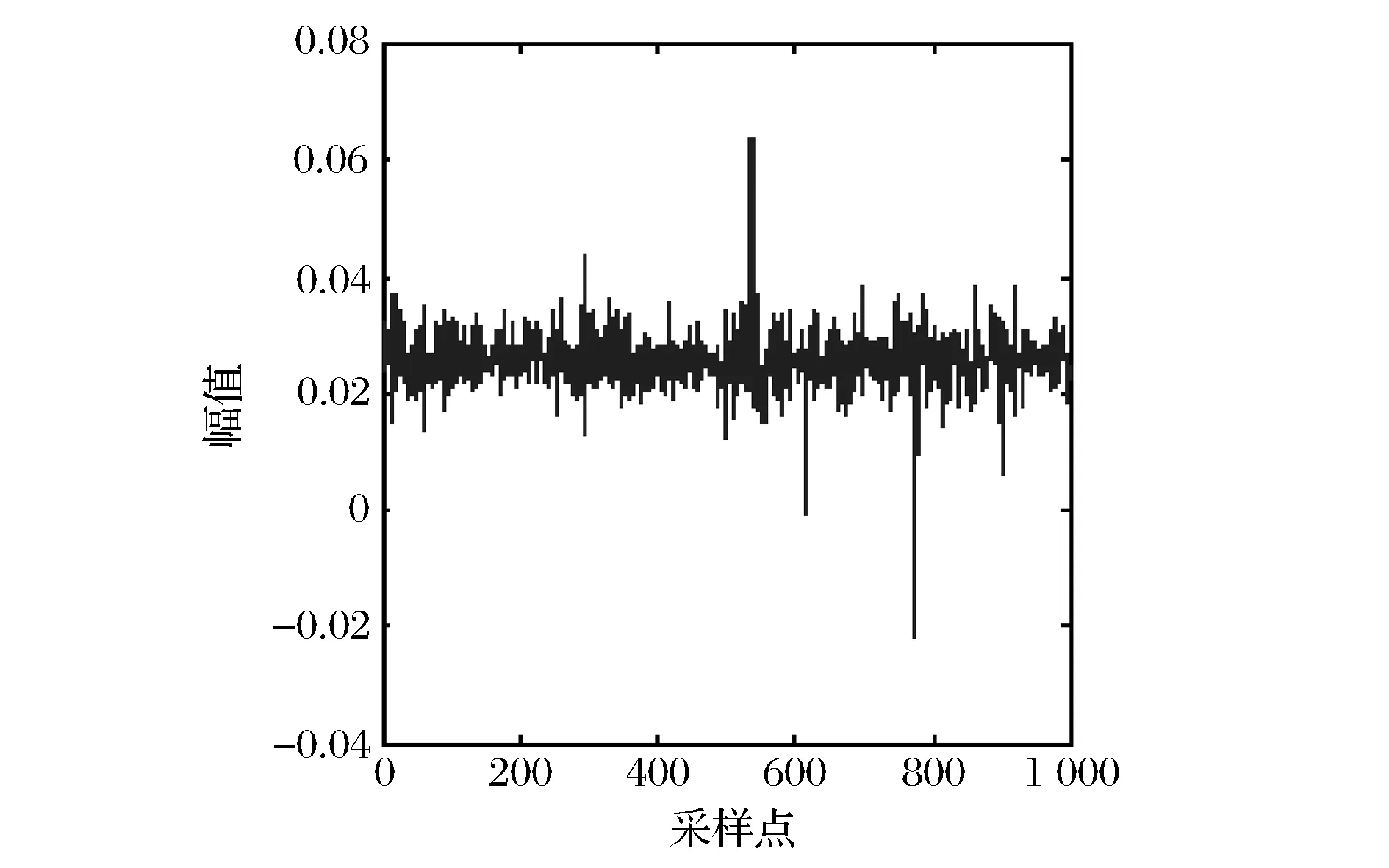
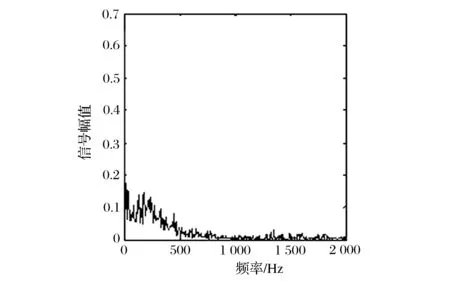
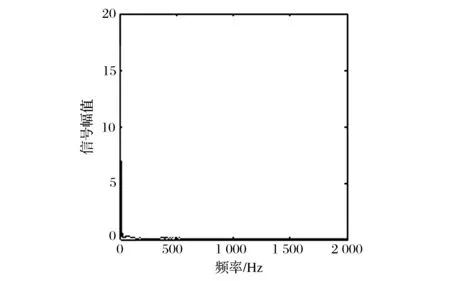
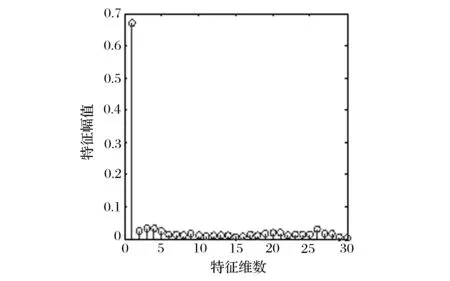
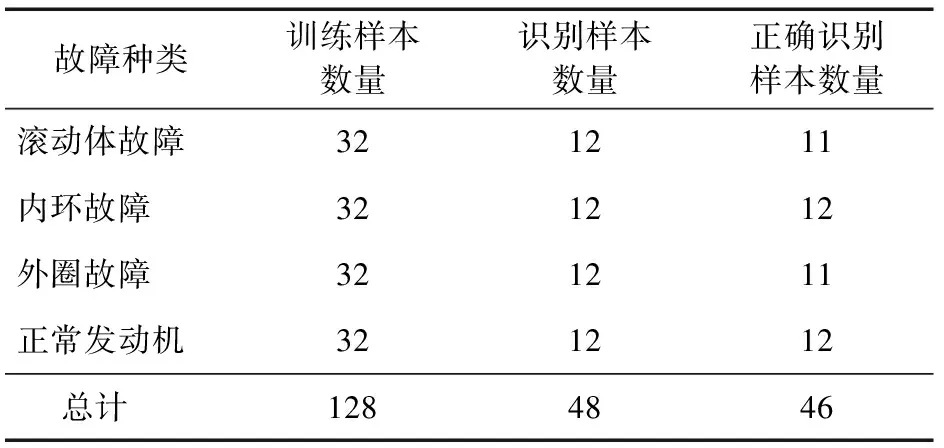
由EMD分解原理可知,IMF分量信号是按从高频到低频的顺序依次排列,且其信号能量亦依次衰减。IMF分量信号表征了故障信号在不同尺度下分解的能量特征,是信号固有的内在模态性质,因此可以作为故障源的特征参数。令Ei表示第i个IMF分量信号ci的归一化能量(以原信号能量作为归一化标准),可得到d维IMF分量信号能量特征参数[E1,E2,…,Ed],d (9) 此外,若对故障信号的HHT时频谱数据在信号时间T内进行积分求和,可得到信号边际谱h(w): (10) 图3所示为汽车内环故障信号的边际谱,表征了故障源生成信号的能量在不同瞬时频率上的累积量大小,可以作为表征故障性质的特征参数。由边际谱图可知,其能量分布的主要频率范围为0~500 Hz,剩余频率处能量较小,无明显变化,可等同为噪声信号处理。 图3 汽车内环故障信号边际谱 为准确提取故障信号的边际谱区域变化特征,首先对能量变化的主要区间即0~500 Hz区域进行频率区间量化。即令每20 Hz为一个完整的能量分析区域,将能量变化区间量化分隔为等频率间距的区域,因此可以获取25个能量分析区域,并按频率由低至高顺序依次排列。然后,对第i个分析区域内的边际谱能量求和得到该区域能量参数hi,并以0~500 Hz区域的边际谱能量总和h0作为标准进行特征尺度归一化,得到该区域的特征参数Hi即 Hi=hi/h0 (11) RBF神经网络能够逼近任意的非线性函数,而且克服了BP神经网络训练速度慢、存在局部极小值的缺点,具有良好的泛化能力,并有很快的学习收敛速度,已成功应用于非线性函数逼近、时间序列分析、数据分类、模式识别、系统建模和故障诊断等领域[6-7]。故本文采用RBF神经网络来验证上述故障信号特征的有效性。 图4所示,RBF网络是一个三层的网络,除了输入输出层之外仅有一个隐含层。输入层节点负责传递信号参量至隐含层;隐层中的转换函数一般是局部响应的高斯函数;而输出层节点通常是简单的线性函数,负责判断结果的输出。其中,RBF神经网络的输入层到隐含层实现输入参量的非线性映射,第i个隐含层节点的高斯响应函数一般取: (12) 式中:ui为第i个隐含层节点的输出;X=[x1,x2,…,xM]为输入层信号参数;σi为第i个隐含层节点的标准化常数。 图4 RBF神经网络结构 在验证所提取的故障特征参数时,首先,将各种故障样本信号经上述算法处理得到一系列故障特征参数,并构成多组各种故障状态下的特征向量作为RBF神经网络的训练输入;然后,利用这些特征向量训练得到RBF神经网络参数;最后,即可对测试样本进行故障特征提取并输入该网络进行故障诊断。 首先,利用上述奇异值分解降噪算法对采集的汽车发动机故障振动信号进行降噪处理,并验证分析处理结果。其中,振动采集信号的采样频率为4 000 Hz,采集时间长度为0.25 s。图5所示为带噪振动信号的降噪后效果。由仿真结果可以看出,原始振动信号在采集过程中受到了一定的噪声污染,若将此原始带噪信号直接进行故障特征提取,势必影响特征参数的提取精度。经过本文降噪算法的处理,去除了大部分的噪声信号,振动信号的时域波形更加清晰,提升了采集信号的信噪比,为进一步准确诊断故障提供了良好条件。 (a)原始信号 (b)降噪信号图5 振动信号降噪效果 利用某型汽车发动机的两种故障样本信号进行特征提取分析。故障样本分别为该型汽车发动机轴承内环故障和外圈故障信号。图6(a)为内环故障信号边际谱,容易看出在0~500 Hz频率范围内,故障频率特征明显存在,生成了较多的频率峰值,包含了较丰富的故障特征信息。图7(a)为外圈故障信号边际谱,其在0~500 Hz频率范围内的频率变化较为平缓,且无明显频率峰值,故障能量积累不明显,与内环故障信号边际谱有着明显的区别性特征。图6(b)与图7(b)分别为内环故障信号与外圈故障信号特征参数提取结果,其中1至25维特征参数即为边际谱区域变化特征,26至30维特征为IMF分量信号能量特征参数。对比可以看出,两种特征参数形成的向量在幅值上有着较大的区别,即两种故障信号在频率域的特征有着本质区别,且IMF分量信号能量亦不相同。因此,本文所提取的边际谱区域变化特征与IMF分量信号能量特征两种参数可以有效区分该两种故障信号。 (a)边际谱 (b)特征参数图6 内环故障信号边际谱与特征参数 (a)边际谱 (b)特征参数图7 外圈故障信号边际谱与特征参数 为验证上述特征提取算法对于汽车发动机故障诊断的有效性,利用RBF神经网络训练故障样本特征数据,并对故障信号进行识别率计算。样本数据集包含4种工况下的汽车发动机振动信号,即内环故障信号、外圈故障信号、滚动体故障信号及正常发动机信号,且每种故障的样本数据量为44组。实验过程中,利用每种故障样本的前32组数据共计128组作为RBF神经网络的训练样本,每种故障样本的剩余12组数据共计48组作为识别样本进行有效性验证。其中,RBF神经网络的输入为30维的特征参数,隐含层为1层,输出为单输出,分别用1、2、3、4代表滚动体故障、内环故障、外圈故障、正常4种判别结果。在训练过程中设定目标误差为0.001。 图8所示为RBF神经网络在训练故障样本特征数据时的误差变化曲线,经过128次迭代训练,该网络成功收敛到设定的目标误差,完成了训练过程。表1为RBF神经网络故障诊断测试结果。由表1可知,识别样本数量为48,正确识别的样本个数为46,故系统正确识别率为95.83%,亦验证了上述算法所提取特征参数的有效性。 图8 RBF神经网络训练误差变化曲线 表1 RBF神经网络故障诊断测试结果 为解决基于汽车发动机振动信号处理的故障诊断问题,首先,构造了所采集振动信号的截断矩阵,利用奇异值分解实现了振动信号的降噪预处理,实际数据处理结果表明该方法可以有效降低采集中所受到的噪声影响;然后,利用HHT方法提取了汽车发动机振动信号的IMF分量信号能量特征与边际谱区域变化特征两种参数作为RBF神经网络的输入,并利用故障样本对该网络实现训练与识别。实验结果表明,上述特征参数可以有效表征故障信号的时频域变化特点,可以作为汽车发动机故障的诊断依据。 [1] 王醇涛,陆金铭.运用HHT边际谱的柴油机故障诊断[J].振动、测试与诊断,2010(8):465-468. [2] 宋越,孙涛,贾然,等.基于Hilbert-Huang变换的发动机气门间隙故障诊断研究[J].组合机床与自动化加工技术,2016(1):74-77. [3] 赵学智,叶邦彦,陈统坚.矩阵构造对奇异值分解信号处理结果的影响[J].华南理工大学学报(自然科学版),2008,36(9):86-91. [4] SHILPA R, PRABHU S S, PUTTASWAMY P S. Power quality disturbances monitoring using Hilbert-Huang transform and SVM classifier[C]// International Conference on Emerging Research in Electronics, Computer Science and Technology, IEEE, 2015. [5] HAMDAD N, HAMMOUCHE K. Hilbert Huang Transform and pattern recognition to detect defects in induction motor[C]// International Conference on Electrical Engineering,IEEE, 2015. [6] KONDAIAH V V, RAO J S, RAO V V S. Estimation of loss factor and system parameters of active magnetic thrust bearing using RBF neural networks and differential evolution[C]// IEEE Workshop on Computational Intelligence: Theories, Applications and Future Directions. IEEE, 2015. [7] VERMA R N, JAIN K, RIZVI M A. Efficient face recognition method using RBF kernel and genetic algorithm[C]// International Conference on Computer, Communication and Control,IEEE, 2015. (编辑:张峰) Automobile Engine Fault Diagnosis Based on HHT and Neural Network HAN Bo1,2 (1.Information Science and Engineering Institute of Circuits and Systems, Lanzhou University, Lanzhou 730000, China; 2.Unit 69019, Urumqi 830017, China) To solve the fault diagnosis problem of automobile engine based on vibration signal processing, the paper firstly pretreats noise reduction of collected signal with truncated singular value decomposition method to obtain purer vibration signal. Then, it conducts decomposition and time frequency analysis on collected signal with signal processing theory of HHT (Hilbert-Huang transform) and extracts component signals and marginal spectrum region characteristics as the basis of fault diagnosis and identification of automobile engine, and makes comparative analysis on feature fusion result in different fault conditions. Finally, it trains fault samples with RBF (radial basis function) neural network and carries out training and recognition of many kinds of fault data. The actual fault data processing result shows that the characteristic parameters can effectively represents the time-frequency domain variation characteristics of fault signal, which can be used as the basis for the fault diagnosis of automobile engine. fault diagnosis; automobile engine; Hilbert-Huang transform; RBF neural network 2016-11-10; 2016-12-20. 韩 博(1978—),男,硕士,工程师. 10.16807/j.cnki.12-1372/e.2017.03.012 U464 A 1674-2192(2017)03- 0047- 06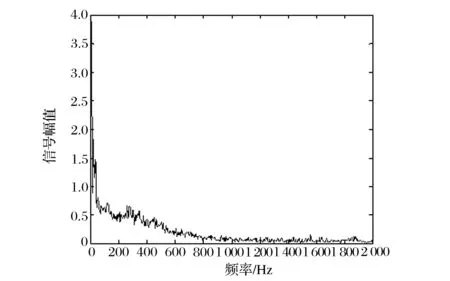
3 基于RBF神经网络的故障诊断

4 仿真分析



5 结 语
