一种大数据背景下的图像特征提取算法
2017-03-30常俊生刘慧青张永杰
常俊生+刘慧青+张永杰

【摘 要】提出一种基于中轴变换的图像骨架特征提取算法,结合Hausdoff距离方法与二次误差度量方案,对图像数据进行简化,最终获得简洁鲁棒的骨架特征。使用自定义的数据集进行验证,实验证明,使用中轴变换的图像骨架提取方法对边界噪声具有良好的抵抗性,在不明显影响提取骨架速度的同时,能够保证图像骨架的精度。
【关键词】大数据 图像处理 中轴变换 图像骨架特征
An Image Feature Extraction Algorithm Based on Big Data
[Abstract] An image feature extraction algorithm of image contour based on medial axis transform was proposed in this paper. Combined with Hausdoff distance method and quadric error metric, the image data can be simplified to get the concise robust contour feature. Experiments demonstrate by the custom data set that, on one hand, the proposed method has the good resistance to the boundary noise; on the other hand, it guarantees the accuracy of image contour without apparently impact on the contour extraction speed.
[Key words]big data image processing medial axis transform image contour feature
1 引言
大数据的飞速发展对海量数据的高效处理提出了很高的要求。图像数据是大数据的重要组成部分,因为图像通常为高维数据,并且含有丰富的信息,因此对海量图像数据的存储、传输、处理等来说都是重要课题。因此,对海量图像进行处理,通常通过聚类分析进行特征学习得到目标图像。
在图像处理领域内,骨架便是一种良好的图像特征。目前对于骨架尚无统一的定义,通常认为骨架是与目标图像的拓扑结构相一致的细曲线。它能够反映图像数据的拓扑结构,除此以外,图像数据骨架特征在图像匹配、图像检索、数据压缩、形状变换等应用中也发挥着重要作用。
本文提出一种基于中轴变换的图像数据骨架特征提取算法,联合Hausdoff距离方法与二次误差度量方法,对初始计算的中轴变换进行进一步处理,最终得到简洁鲁棒的骨架特征。
2 相关工作
大數据技术的发展给传统图像领域带来了巨大的技术变革。随着互联网的发展,图片数据指数式增长,在海量的图片数据中获取目标信息图片,这是一项艰巨的任务[1]。分布式处理、云计算、机器学习等领域技术的发展给海量数据的处理带来了新的机遇与挑战。数据量的增加给图像检索等应用增加了难度[2-3]。因此,需要一种简洁、便于存储传输、检索的表达方式表示图像数据。其中,骨架便是一种能够反映图像骨架拓扑信息的良好的表达方式。
在图像处理领域内,目前骨架还没有明确统一的定义,常用中轴对骨架进行精确定义,因此本文对于骨架与中轴不加区分。骨架是对象检测的一个重要信息,它描述了对象各个部分之间的联系,即它与对象的拓扑是一致的[3-5]。从预分割的图像中提取骨架是一个热门的课题,提取的骨架特征能够运用在基于形状的对象匹配和识别中[6]。
本文提出一种使用中轴变换的图像骨架特征提取方法。在预分割的图片上,提取出目标对象轮廓,再计算轮廓的中轴变换。得到中轴后,先通过单边Hausdoff距离方法去除毛刺中轴,再通过改进的二次误差边折叠方法对其进行简化,最终得到简洁鲁棒的骨架。
3 使用中轴变换的图像特征提取算法
3.1 中轴的基本定义
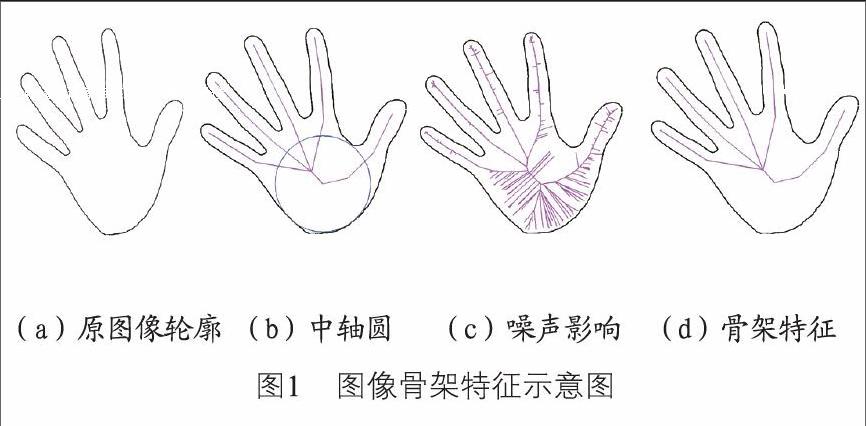
Blum在1967年提出中轴的概念,中轴描述为模型内最大内切圆圆心与半径所组成的集合。如图1所示,(a)图为目标图像轮廓,(b)图为中轴的定义,其中蓝色的圆即为最大的内切圆,(c)图中粉色的线即为通过计算轮廓的Voronoi图得到的中轴,(d)图中粉色的线即为骨架。由图1(c)可以看出,计算轮廓边界得到的中轴含有很多噪声,称之为毛刺。这些毛刺,不利于骨架的应用,因此,需要对这些毛刺进行简化处理。
3.2 中轴简化规则
Sun等人[7]使用单边Hausdoff距离对中轴进行简化,单边Hausdoff距离是指所有中轴点到所有轮廓点欧式距离减去半径之差的最小绝对值的最大值。该距离能够反映中轴简化前后模型的改变程度。该方法能够得到简洁光滑的骨架,不过该方法在极端简化情况下,比较耗费时间。
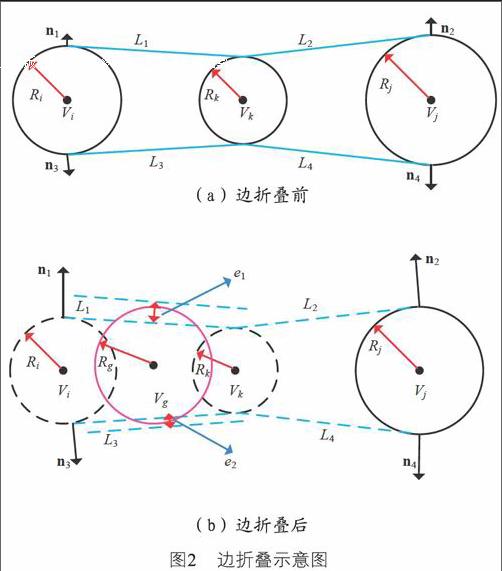
Thiery[8]改进二次误差度量[9],并将其运用于三维中轴球的简化。Li[10]等人使用球二次误差度量,对中轴网格进行简化。二次误差度量方法在中轴简化过程中,在极端简化情况下,不能很好地保证中轴的稳定性。所以本文首先使用单边Hausdoff距离方法对初始中轴进行简化,因为单边Hausdoff距离方法在极端简化情况下不能保证细节特征并且耗时严重。考虑到图像数据的特性,再使用二次误差度量的方法进行简化。实验证明,该方法能够较高效地提取出简洁鲁棒的图像骨架特征。边折叠示意图如图2所示:
3.3 改进的二次误差度量算法
二次误差度量方法常使用在网格简化过程中,本节将介绍改进二次误差度量算法,并将其用在中轴简化过程中。如图2所示,每个圆都为中轴圆,(a)图为简化前的中轴图,(b)图为简化后的中轴图,图中每个中轴圆均由v(x,y,r)组成,其中(x,y)为中轴圆圆心坐标,r为中轴半径,则线段vivk为一条中轴边eij,其中L1、L2、L3、L4分别为对应中轴圆的外公切线。图2(a)中,n1、n2分别为vivj的外公切线的向外单位法向量。图2(b)中蓝色的中轴圆vg为中轴边eij经过边折叠后得到,以此达到简化的目的。简化过程中的代价函数定义为E(vi,vj)=e12+e22。vivj简化后得到vg。为了统一计算,单位法向量n,再加一个分量1,即(x,y,1)。
因此,邊折叠代价公式如下:
其中vx即为边折叠后新中轴圆的位置。由Garland[9],
对式(1)进行简化得:
其中,
A=n1.n1T+n2.n2T,
,
。
通过二次误差最小化,则得到:
3.4 边折叠算法
根据误差函数,则每条中轴边都含有一个折叠代价,对所有边折叠代价进行排序,选择最小的折叠代价的边进行折叠简化,这样不停迭代,直到达到指定的简化程度。
3.5 图像骨架特征提取算法
本文提出的图像骨架特征提取算法,在预分割的图像上首先获取图像轮廓,再计算轮廓的中轴变换,得到初始的中轴。由于初始的中轴含有大量的噪声信息,如图1(c),因此,需要对得到的中轴进行进一步处理。本文首先通过单边Hausdoff距离方法,对初始中轴进行简化,该过程简化是通过直接去除毛刺,当去除毛刺后,该中轴的Hausdoff距离保持在给定阈值以内。再使用改进的二次误差度量进行简化,最终得到简洁的骨架特征。图像骨架特征提取算法如下所示:
(1)输入所有中轴边以及中轴点集合,给定单边Hausdoff距离阈值ε,给定二次误差度量的剩余中轴点个数N。
(2)计算每条中轴边去除的Hausdoff距离,选取Hausdoff距离最小的边进行去除,判断去除后单边Hausdoff距离是否大于ε。是,跳转到(3);否则,跳转到(2)。
(3)计算每条中轴边的二次误差代价,对所有中轴边进行排序,选取最小的中轴边进行边折叠,将该中轴边的两个端点中轴圆从中轴圆集合中去除,将新得到的中轴圆加入该集合,更新所有与之相关联的中轴点的三元组系数。
(4)判断剩余中轴点集合中中轴点个数是否小于N。是,结束;否则,跳转到(3)。
4 实验设计与结果分析
4.1 实验设计
本文实验是在Windows7 Intel i7 8 GB内存上使用VS2013 C++完成的。实验中,使用OpenCV对图像进行轮廓提取。得到目标图像轮廓后,使用CGAL中Delaunay三角化函数计算初始中轴。最后,通过单边Hausdoff距离方法对得到的中轴进行简化。简化到给定阈值的时候,再使用二次误差度量法进行简化,最终得到简洁鲁棒的骨架。由于计算单边Hausdoff距离的时间复杂度是O(n2),故本实验时间复杂度即为O(n2)。
本文在自定义图片数据集上进行实验,对得到的图片进行归一化处理,所有图片像素均在200×200~
300×300之间,并且得到的轮廓点数在800~1200。ε取0.05~0.08时,实验结果较好,N取15~25时,最终得到的骨架准确性较高。不作特殊说明,本文ε取0.05,N取20。
4.2 实验结果
图3给出了本文算法与基于单边Hausdoff距离方法的实验比较结果。表1给出了算法执行的相关参数以及数据。从表1可看出,单边Hausdoff距离方法简化中轴比较耗费时间。另外,在极端简化的情况下,本文算法能够在不耗费太多时间的同时,提取得到简洁鲁棒的骨架特征。
另外,在简化过程中,首先使用单边Hausdoff距离再使用改进的二次误差度量方法。这两者之间切换时间,实验证明,剩余中轴点数在初始中轴点数的10%时进行切换,此时ε在0.05~0.08之间取值。
5 结束语
移动媒体与互联网的发展促进了图像大数据的指数式增长。为了能够高效地处理、检索、存储这些海量数据,需要对它们进行进一步处理。对原始图片数据进行特征提取,这样便于处理检索存储。本文提出的基于中轴变换的图像特征提取算法能够简化图像,得到简洁鲁棒的骨架特征,为后续的处理提供了便利。在保持精度的同时,也能保持图像特征的鲁棒性。
参考文献:
[1] 赵锐. 基于大数据背景下的图形处理技术变革探索[J]. 电子测试, 2014(20): 143-144.
[2] 汪淼,张方略,胡事民. 数据驱动的图像智能分析和处理综述[J]. 计算机辅助设计与图形学学报, 2015,27(11): 2015-2024.
[3] 刘智慧,张泉灵. 大数据技术研究综述[J]. 浙江大学学报:工学版, 2014,48(6): 957-972.
[4] 张晶,冯林,王乐,等. MapReduce框架下的实时大数据图像分类[J]. 计算机辅助设计与图形学学报, 2014,26(8): 1263-1271.
[5] 刘利钊,洪江水,刘莉莉,等. 面向大数据图像处理的尺度空间挖掘算法及应用[J]. 上海交通大学学报, 2015,49(11): 1731-1735.
[6] Demirci M F, Shokoufandeh A, Keselman Y, et al. Object recognition as many-to-many feature matching[J]. International Journal of Computer Vision, 2006(2): 203-222.
[7] Sun F, Choi Y K, Yu Y, et al. Medial meshes for volume approximation[J]. Computer Science, 2013.
[8] Thiery J M, Guy ?, Boubekeur T. Sphere-Meshes: shape approximation using spherical quadric error metrics[J]. ACM Transactions on Graphics (TOG), 2013(6): 178.
[9] Garland M, Heckbert P S. Surface simplification using quadric error metrics[A]. Proceedings of the 24th annual conference on computer graphics and interactive techniques[C]. 1997: 209-216.
[10] Li P, Wang B, Sun F, et al. Q-MAT: Computing Medial Axis Transform By Quadratic Error Minimization[J]. ACM Transactions on Graphics (TOG), 2015(1): 8.
