全通滤波器调整相位的原理
2017-03-30高维忠
高维忠
【Abstract】In this paper, the author introduced the related concepts and basic principle of the all pass filter which can adjust the audio signal phase.
【Key Words】all pass filter; phase; phase difference; amplitude; phase frequency characteristic; group delay
近年来,利用全通滤波器来改善音色的文章屡见不鲜,如利用全通滤波器调整相位以及用全通滤波器来补偿两个声波间相位差等。鉴于此,笔者就全通滤波器的原理谈一些个人的认识,以供参考。
1 相位和相位差
声频行业的许多技术人员都希望通过在扩声系统中加入全通滤波器来调整相位关系,从而弥补由于相位问题而引起的声音缺陷。然而,前提是必须了解“相位”和“相位差”这两个基本概念。
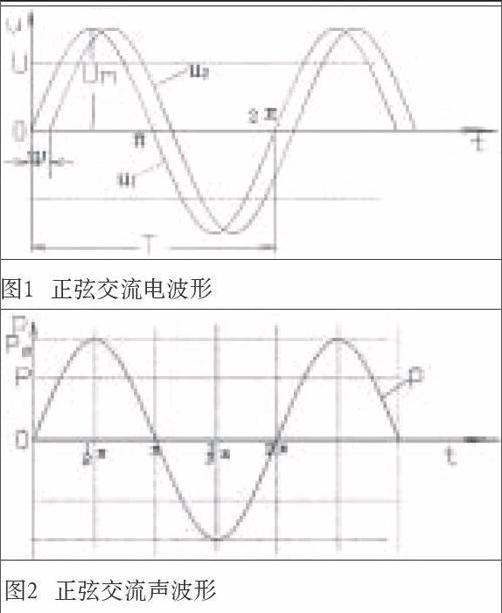
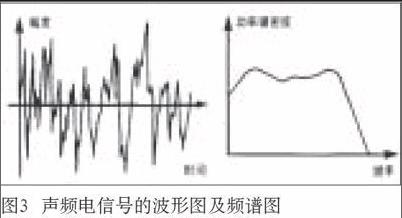
声频信号具有频率、幅度、声速、相位、声程等相关特性,其可听声波的频率范围(即“声频范围”)是20 Hz到20 kHz。但是,绝大多数声音不是单一频率的正弦波信号,而是由许多频率的正弦波信号组合而成的,其中最主要的就是声音的基音(基波),还有很多个谐音(谐波),这些谐音的频率是基音频率的不同整数倍,例如2倍、3倍、4倍……n倍,通常可以称为二次谐波、三次谐波、四次谐波等等,最后组成“复合”的声音幅度时间曲线,也就是波形图。如图1所示是正弦波交流电的波形,横轴是时间轴(t),纵轴是电压轴(U),其中电压瞬时值用小写的u表示,Um为最大值,也称峰值,图示u1和u2两个正弦波,ψ是u1和u2两个正弦波之间的相位差,T是周期,一个周期T中包含2π弧度的角度,或者说是360°角度。实际上,声波正弦波的波形也是这样的,只不过将纵轴的幅度用声压来代替电压而已,正弦波声波的波形图见图2,图中横轴是时间轴(t),纵轴是声压轴(p)。在电声设备中传输和处理的声频信号是电信号,最后经过扬声器的换能后辐射出来就是声信号了。
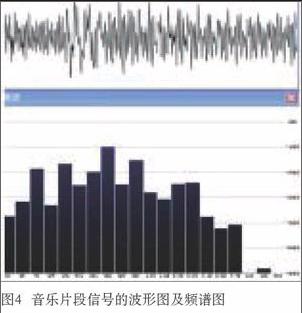
那么就声波的波长λ来说,可以从20 Hz时的波长17 m逐步减小到20 kHz时的波长1.7 cm。不同周期的声波对应不同的波长。而人们平时听到的声音中包含了许多频率成分,这些频率成分是指正弦波或者叫纯音,也就是前面说的可闻声频率范围内的正弦波频率。如图3所示,是声音信号中某个片段的波形图和频谱图,声波信号中包含较宽频带的正弦波。图4是音乐片段信号的波形图和频谱图,这里的频谱图是以1/3倍频程带宽来显示的。从图3和图4可以看出,该信号实际上是由很多不同强度和不同相位差的频率的正弦波组合而成的。
对于单个声源,存在相位问题。但声波从声源辐射出来后,总要在媒质中向远处传播的,离开声源的距离不同,声波的相位移就不同。因为声波在空气中是以约340 m/s的速度传输的(这里不研究空气温度变化等因素对声速造成的变化),其实在不同距离处只是在不同时间听到该声音,各频率(基波和各次谐波)之间的相位关系没有改变,理论上并不影响音色。
2 相位失真
一般来说,大家认为信号的相位失真在听感上是基本听不出来的,或者说基本不影响听感的,所以,一直没有将相位失真作为对扩声设备的技术指标之一来进行考量。实际上,声频电信号在音响设备中传输会带来一定的相位失真,尤其是设备的频率带宽不足的情况下,电路本身对不同频率(基波和各次谐波)的信号会产生不同附加相移,从而引起信号的相位失真。如果设备中对声频信号处理中用上了(高通、低通、带通、带阻)滤波器或频率均衡器(其实就是利用带通滤波器来达到目的的)来调整信号的幅频特性,那么产生的附加相移就会更严重,尤其是在截止频率附近,其相位失真更严重。在空间传输过程中,不同频率的声波移动相同的距离,产生的相位移是不同的,相移与频率成正比,例如传输距离为3.4 m,对于50 Hz的声波来说是移动了半个波长(1π弧度,或者说180°),对于100 Hz的声波来说是移动了1个波长(2π弧度,或者说360°),而对200 Hz的声波来说是移动了2个波长(4π弧度,或者说720°)。只有这样才能使声音信号经过传输后的波形不发生变化,即保持原来的音色。
3 相位补偿
相位补偿包括两个方面:
(1)补偿的是哪两个声音源傳过来的声波之间的相位差
一般来说,两只扬声器产生的声音之间的相位差与听音位置到这两只扬声器的距离有关。如果听音位置到两只扬声器的距离完全相等,则理论上应该同时听到两只扬声器所发出的同一声音。从相位角度考虑,则是同相位的声音。如果听音位置与两只扬声器的距离不等,那么在听音位置就会先听到距离近的扬声器所产生的声音,后听到距离远的扬声器所产生的声音,这种现象是普遍存在的。两只扬声器的声波在听音位置由于存在时间差而先后到达,出现各个频率上不一致的相移(这是必然的,因为频率不同,波长就不同,相位差也不同),引起声波的干涉现象,造成梳状滤波器效应而改变音色。不同听音位置上两个声音中由于声波传输距离的不同,各频率产生了很多不同声波的相位差,所以,要绝对地、完全地补偿这种相位差是不可能的。
同一全频带扬声器中高频扬声器单元和低频扬声器单元由于安装位置造成振膜不在同一平面上,由前后位置的不同而引起的相位差问题,也许值得考虑,但是既然一只单元产生高频声波,另一只单元产生低频声波,那么牵涉到相位差问题的只是在分频点附近。随着频率偏离分频点,扬声器的两只高低音单元所产生的声压大小不同,相互干涉的影响程度减小,偏离分频点越远,两个单元产生的声压相差就越大,那么干涉造成的影响就越小。
另外,低音扬声器单元的振动系统质量比较大,惯性也比较大,或者说瞬态特性比较差,也会引起分频点附近高音单元和低音单元产生的声波出现相位差问题。当然,如果弥补到高音单元和低音单元的声波同时到达扬声器表面位置,情况会更好,所以不妨引入延迟来补偿,这里补偿的是时间差,而不是相位差(因为频率不同相位差也是不同的)。
(2)补偿哪个频率出现的相位差
全通滤波器并不能对某个频率的相移单独进行改变,例如仅仅对某个频率的相移增大多少度或减少多少度是无法实现的。全通滤波器产生“群延迟”,可以作为延迟器来使用,会产生所谓的“线性相移”(实际上全通滤波器的相位移并不能完全呈现线性变化的,见本文后面说明),即随着频率的升高,相位移也线性地增大。
4 全通滤波器
全通滤波器(APF -All Pass Filter),延遲最大平坦的滤波器,也叫贝塞尔(Bessel)滤波器,也叫汤姆逊(Thomson)滤波器。全通滤波器又称线性相移滤波器、相位均衡器。只有衰减随频率变化的幅度特性(幅频特性)还不能完全说明滤波器的传输特性。在使用脉冲信号的各种通信领域,滤波器设计者必须考虑很多因素,例如延迟、上升时间、超量、衰减率、瞬态振荡等等。理想的情况是平坦延迟,意味着通过滤波器的各种频率均延迟一样的时间,因而不发生散射影响,使输出脉冲保持输入的原形。全通滤波器的相位响应(相频特性)基本呈现线性状态,也称相位均衡器,具有一定的“群延迟”, (根据定义,相移的导数叫群延迟,)通常可以作为延迟器用。全通滤波器具有平坦的幅频响应,也就是说全通滤波器并不衰减任何频率的信号。
全通滤波器虽然并不改变输入信号的幅频特性,但它会改变输入信号的相位。利用这个特性,全通滤波器可以用做延时器、延迟均衡等。但是延迟时间一般不长,并且还随着选定的极点角频率ωx升高,延迟时间也相应地变短,即便采用多级二阶全通滤波器级联起来,也不能构成很长时间的延迟,所以,对于后排补声扬声器与主扬声器之间的声程差补偿的延迟,一般采用专门的延时器来完成。目前,数字延时器的延时技术是将模拟音频信号转换成数字信号,然后存放到存储器中,只要设定了需要延时多长时间,经过这个需要的延迟时间再次从存储器中将信号调出来即可,所以,延时过程中基本不产生失真,并且设置的延时时间可以很长。
4.1 全通滤波器传输函数
如果将二阶传递函数典型式的零点移到s平面右半部与极点依jΩ轴对称存在时(如图5所示),则传递函数表示式为
从(公式3)可见,全通滤波器在所有频率上的振幅特性均为1,即在所有频率上的输出幅度均等于输入幅度。
由(公式4)可知:ω=0时,φ=0;ω=ωx时,φ=-180;ω=∞时,φ=-360。
同时从(公式4)可知相频特性和Qx有关,Qx越小,则曲线在ω位于0附近的斜率越大(指绝对值,下同),而在ωx附近的斜率越小。反之,Qx越大,则曲线在ω位于0附近的斜率越小,而在ωx附近的斜率越大。相频特性见图6。
4.2 群延迟
4.3 全通滤波器的特性
从(公式4)看出全通滤波器的传递函数的相频特性是非线性的。从(公式6)更进一步看到ω变化时也在变化,不为常数。这说明相频特性的斜率在随ω变化。这显然是所不希望的。但可以找出在一定的频率范围内使其相频特性近似于一根直线的最佳Qx值。其相频特性曲线和直线间的误差可被控制在一定的允许范围内。接近所谓相频特性是线性的,也就是群延迟为接近一常数。结合前面的分析,令两个特定点上的斜率相等,以求出合适的Qx时相频特性在ω=0及ω=ωx这两点的斜率相等。然而,这两点上的斜率相等并不代表在这两点之间的任意点上的斜率也相等,具体数据见表1。
而真正理想的全通滤波器特性应如图8所示。但是实际上做不到,存在一定的误差。
为了更直观地看出相频特性曲线的形状,需计算不同Qx值时的相频特性,以便寻找最佳的Qx值。表1是在Qx=0.707时的值,从中看出ω/ωx在0.1到0.6区间斜率逐渐增长,ω/ωx从0.7以后逐渐减小,直至ω/ωx为1时才稍小于ω/ωx为0.1时的斜率。按照这种规律,频率越高则相移比线性值滞后得越多(因为差值在逐步积累)。前面已经说明过Qx值与相频特性的关系,Qx值越小,则频率低端的相频曲线斜率增大(绝对值,全文都如此),高端则减小。根据分析和计算得到Qx=0.645时,ω/ωx从0.1到1.15区间相频特性的线性度较好,各频率时的相移与真正直线时的误差小于±7°,这个相位误差造成的声波干涉引起的梳状滤波器效应的影响应该是非常小了,具体数值见表2。有了上述结论,便可以设计具体的相移器了。
5 结论
从上面分析可知,在音频系统中使用全通滤波器,主要是利用其群延迟特性构成一定时间的延时器,使两个不同声源产生的声波能够同时到达某一位置(例如全频带扬声器中高低音单元产生的声波同时达到扬声器前表面),尽量减小由于两个声波先后到达某个位置而引起声波的干涉,造成梳状滤波器效应而影响音色。但是,绝不能通过全通滤波器来改变信号在某个频率上两个声源的声波存在的相位差。
进一步探讨,如何知道某两个声波在哪个频率上有多少角度的相位差的,既然不知道这些数据,又如何谈利用全通滤波器来改变相位以达到将两个声波的相位差消除的问题呢?还有就是前面的分析已经证明全通滤波器并不是真正的线性相位移,只能说是接近于线性相位移,所以,使用全通滤波器后,由于新增了附加的非线性相位移,反而将原节目信号构成的各频率之间的原始相位关系搞乱了,反而变得不符合原始信号的原状。事实上,常用改变幅频特性的高通滤波器、低通滤波器、带通滤波器、带阻滤波器(陷波滤波器)及频率均衡器,其实际传输特性中的幅频特性在通带内也只是理论上大致平坦,实际上是有波动的,例如切比雪夫滤波器就明确地规定了通带内有0.5 dB和1 dB波动的零极点位置的数据;并且,规定幅频特性-3 dB频率点作为滤波器截止频率点;证明在通带内的增益不是完全平坦的。所以,无论使用滤波器来调节幅频特性,还是使用相位均衡器来作为延迟器,都会带来幅度或者相位的非线性变化。
