地震作用下复阻尼调频质量阻尼器减震结构优化设计

田 欢

(中国中元国际工程有限公司，北京 100089)

地震作用下复阻尼调频质量阻尼器减震结构优化设计

田 欢

(中国中元国际工程有限公司，北京 100089)

分析了简谐激励和平稳随机激励条件下，复阻尼调频质量阻尼器(TMD)和主结构的二自由度减震结构体系的稳态地震响应，建立了动力学平衡方程，推导了复阻尼TMD的阻尼和频率最优参数的理论公式，并分析了该二自由度减震结构体系在多条地震波作用下的减震效果，对比了复阻尼TMD和粘滞阻尼TMD减震效果的差异，结果表明：复阻尼TMD的减震效果接近于粘滞阻尼TMD的结果，在应用TMD减震技术时，复阻尼TMD也是一种选择。

复阻尼，TMD，简谐激励，白噪声激励，地震波激励

0 引言

近些年来，在调频质量阻尼器的研究中主结构和TMD子结构采用的都是粘滞阻尼。粘滞阻尼TMD减振结构的优化设计理论已经发展的很成熟，在机械振动和土木工程的振动控制中都有了成功的应用[1-5]。

相对于粘滞阻尼而言，复阻尼在TMD减振结构中的研究比较晚。文献[6]对复阻尼TMD减振结构的最优参数进行了研究，结果表明复阻尼TMD的减振效果与粘滞阻尼TMD的减振效果接近，但作者没有给出设计公式。

丁文镜[7]对文献[6]的研究成果做了部分介绍，之后对复阻尼在TMD中应用的研究文献就很少了。

本文将基于地震激励下主结构无阻尼的二自由度力学模型，对简谐激励和白噪声随机过程激励下复阻尼TMD减震结构的地震响应进行分析，推导最优参数的理论公式。对采用最优参数TMD的上述二自由度结构在22条地震波作用下的动力响应进行分析，研究复阻尼TMD和粘滞阻尼TMD减震效果的差异性。

1 简谐激励下复阻尼TMD最优参数的理论解

如图1所示的地震作用下主结构无阻尼的二自由度结构力学模型，其对应的运动方程如式(1)所示。

(1)

其中,m0，k0，m1，k1分别为TMD减震结构中主、子结构的质量和刚度；fd为子结构的阻尼力，当采用复阻尼时，阻尼力按式(2)计算[8]。

(2)

(3)

(4)

定义A0=R0/ys，A1=R1/ys，代入式(4)中,消除ys后解得：

(5)

式(5)的模为：

(6)

其中,β0,β1分别为主、子结构的位移响应的动力放大系数。

B1=(g4μ+(f2-g2)(-1+g2(1+μ)))。

B2=f2(-1+g2(1+μ))。

B3=g2-f2(1+μ)。

B4=f2(1+μ)。

文献[9]给出了主结构无阻尼的TMD减振结构中放大系数随输入频率比的变化曲线，当子结构取不同的阻尼时，这些曲线有公共点。文献[10]推导了简谐激励下主结构无阻尼的TMD减振体系的最优频率比和最优阻尼比，最优频率比由两个公共点对应的位移动力放大系数相等的条件获得，最优阻尼比由曲线的峰值点与公共点重合得到。本文将采用此方法推导复阻尼TMD减振结构的最优参数。对式(6)中β0分别取η趋于0，η趋于无穷得到：

(7)

当μ，f为某定值时，式(7)表示β0随g变化的两条曲线，令两式相等化简得到：

2(1+μ)g4-(2+μ+2f2(1+μ)2)g2+2f2(1+μ)=0

(8)

式(8)中有两个正数解，记为ga,gb。将ga,gb分别代入式(7)的第二式，令二者相等可求得频率比与质量比的关系式，此时的频率比为最优频率比，即：

(9)

将fopt回代可得：

(10)

(11)

将fopt代入式(6)中第一式，当a,b两点的位移放大系数为局部极大值时，求解阻尼比。经复杂地推导后得到a,b两点对应的阻尼参数：

(12)

当质量比μ较小时，按有关文献的方法定义最优阻尼参数，即：

(13)

将上面的结果总结到表1，表1中同时给出粘滞阻尼对应的结果。从表1中可以看出：

复阻尼和粘滞阻尼对应的最优频率比、公共点处频率比、公共点处动力放大系数均相同，最优阻尼参数不同。

表1 简谐激励下TMD减震结构稳态响应优化参数

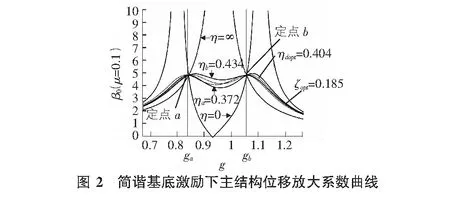
图2给出的是质量比为0.1、频率比取复阻尼对应的最优频率比，阻尼参数分别取0,ηa,ηopt,ηb，∞时β0随g的变化曲线，作为对比，图2中还给出了粘滞阻尼取最优参数(fopt,ζopt)时对应的结果，从图2中可以看出：

1)不同阻尼参数对应的主结构位移反应动力放大系数曲线经过两个公共点。

2)TMD减振结构采用最优参数设计时，在小于ga的区域，复阻尼TMD的位移放大系数小于粘滞阻尼TMD对应的结果，复阻尼TMD的减振效果要优于粘滞阻尼TMD；在大于gb的区域，复阻尼TMD的位移放大系数大于粘滞阻尼TMD对应的结果，粘滞阻尼TMD的减振效果要优于复阻尼TMD，但二者相差不大。

3)TMD采用最优参数设计时，复阻尼TMD对应的位移反应放大系数曲线中的最大值大于粘滞阻尼TMD的结果，但二者相差很小。

2 平稳白噪声激励下复阻尼TMD的最优参数及减震效果

对图1给出的二自由度力学分析模型进行平稳白噪声地震激励，主结构位移传递函数为：

(14)

其中，g=w/w0,主结构位移响应的功率谱为：

(15)

对式(15)在频率域内积分可得它的方差：

(16)

将上面求出的复阻尼TMD的A0(g)代入式(16)，用留数定理得到式(16)的理论解，但结果很复杂。用数值方法求出使方差最小时对应的频率比和阻尼比随质量比的变化曲线，此时的频率比和阻尼比为最优解。用数值拟合方法求出TMD减振体系最优参数的经验公式，如表2所示，作为对比，表2中同时给出粘滞阻尼TMD最优参数的理论公式[7]。

表2 平稳白噪声地震激励下稳态响应优化参数

定义下面参数表示TMD的减振效果：TMD减振结构在平稳白噪声激励下主结构位移方差与单自由度结构在平稳白噪声激励下结构位移方差之比，即：

(17)

图3给出了ζ0=0.05时TMD减震效果随质量比的变化曲线，图4给出了TMD的最优参数随质量比的变化曲线，从图中可以看出：

1)粘滞阻尼的减振效果稍好于复阻尼，但二者相差很小，复阻尼有很好的应用前景。

2)当TMD减振结构的质量比大于0.05时，减振效果大于0。

3)平稳白噪声激励下，复阻尼和粘滞阻尼对应的最优频率比不同，但二者相差不多。

3 地面运动加速度时程激励下复阻尼TMD减震效果

下面考察最优参数配置条件下TMD减震结构的地震响应及减震效果，分析模型为如图1所示的二自由度结构，结构参数取值如下：w0=2π，m0=1，μ=0.1。采用复阻尼时，按简谐激励和按白噪声过程激励给出公式计算的最优频率比分别为0.89和0.94，最优阻尼参数分别为0.4和0.32；采用粘滞阻尼时，按简谐激励和按白噪声过程激励给出公式计算的最优频率比都为0.89，最优阻尼参数分别为0.19和0.15。地面运动加速度时程选取22条地震波，即ATC-63建议采用的远场(距离震中大于10km)地震动记录，峰值都调至1m/s2。

为了便于讨论，计算了相同阻尼比下，w0=2π，m0=1，ζ0=0.05的单 自由度结构在相同地震波作用下的时程响应。根据式(17)思路定义如下减震效果：

(18)

即用TMD减震体系主结构位移幅值相对于5%阻尼比单自由度结构位移峰值的减小百分比。

图5a)给出的是22条地震波作用下主子结构位移响应峰值，其中子结构最优参数按简谐激励条件确定，包括复阻尼和粘滞阻尼。

从图中可以看出：

1)两种阻尼对应的主结构位移响应峰值近似一致。

2)子结构峰值少数地震波作用下稍有差异，复阻尼对应结果稍小于后者。

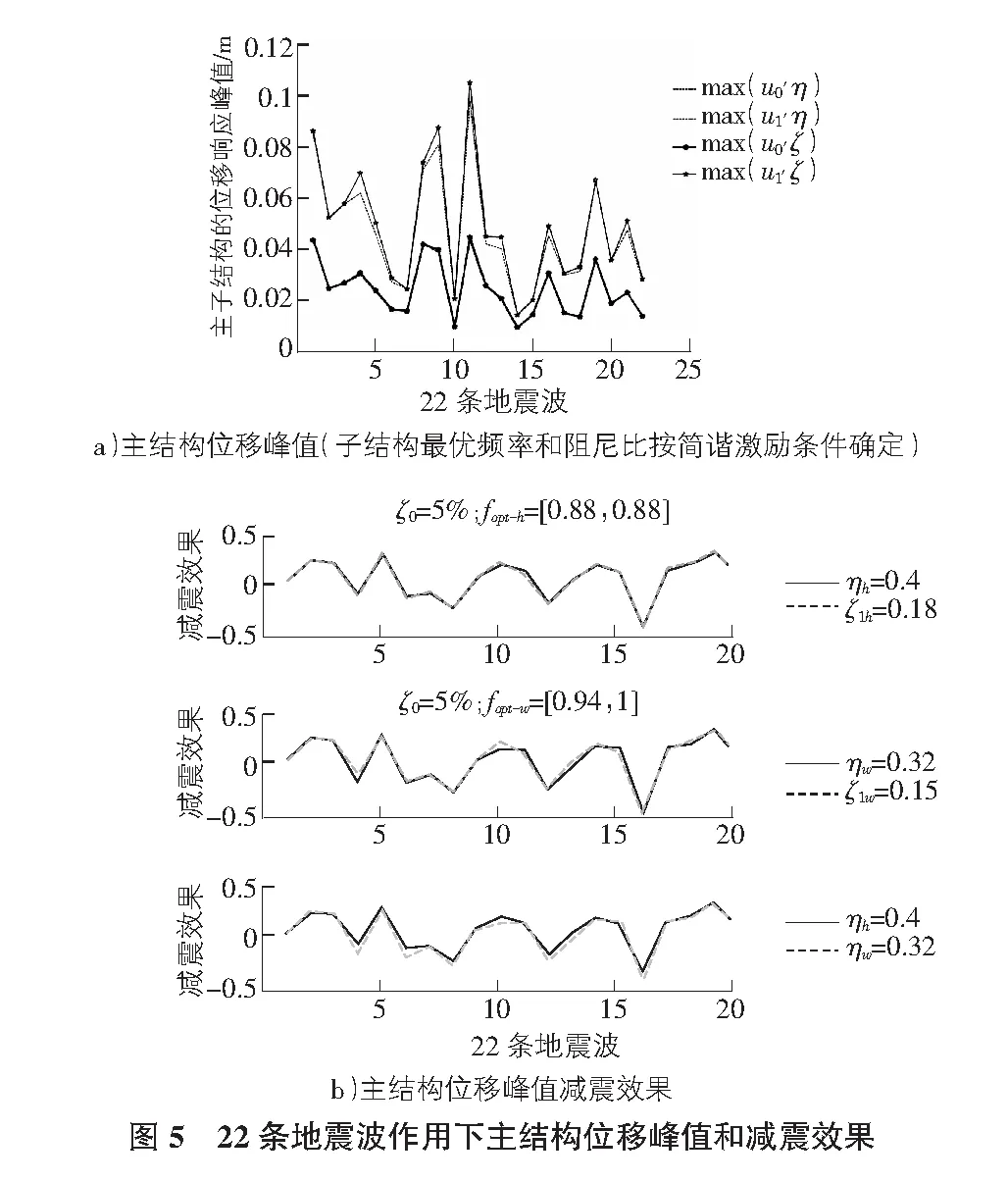
图5b)给出的是22条地震波作用下主结构位移峰值减震效果，确定子结构最优参数时考虑了简谐激励条件和平稳白噪声激励条件，每种时程工况还包括复阻尼TMD和粘滞阻尼TMD两种情况。图5b)中上子图为按简谐激励条件确定子结构最优参数对应的结果，中子图为按白噪声激励条件确定最优参数对应的结果，下子图为按这两种方法确定的最优复阻尼参数对应结构在22条波作用下的减震效果对比曲线。

从图中可以看出：

1)用两种方法确定的两种阻尼最优参数对应的主结构位移减震效果近似一致。

2)基于简谐激励条件和白噪声激励条件确定的优化参数对应的结果稍有差异，但比较小。

4 结论与讨论

对复阻尼在TMD减震体系中的应用进行了研究，推导了简谐激励地震作用下复阻尼TMD的最优参数理论公式，用数值拟合方法给出了平稳白噪声地震激励下的优化参数公式，并对22条地震 波作用下复阻尼TMD减震体系的减震效果进行了分析。得出如下结论：

1)简谐激励下，复阻尼TMD减震结构的最优频率比和粘滞阻尼TMD的结果相同，在公共点处的最大阻尼力和子结构位移也相同。

2)平稳白噪声作用下，复阻尼TMD的减震效果略小于粘滞阻尼，当质量比为0.1时，二者相差0.95%，当质量比为0.5时二者相差2.7%，相差很小。

3)在地震波作用下，两种阻尼对应的TMD减震效果接近，基于简谐激励和白噪声激励给出的最优参数对应的地震波减震效果之间的差异较小。

[1] 王肇民.电视塔结构TMD风振控制研究与设计[J].建筑结构学报,1994(5):2-13.

[2] 翁大根,黄斐骏,周志光,等.某超高层建筑电涡流TMD的减震分析[J].地震工程与工程振动,2014,34(sup):815-821.

[3] 李春祥,刘艳霞.高层建筑TMD风振控制优化设计[J].计算力学学报,2001(1):71-75.

[4] 背户一登.结构振动控制[M].北京:机械工业出版社,2011.

[5] 背户一登.动力吸振器及其应用[M].北京:机械工业出版社,2013.

[6] J. C. SNOWDON.Steady-state Behavior of the dynamic absorber[J].Journal of the Acoustical Society of America,1959,31(8):1096-1103.

[7] 丁文镜.减震理论[M].北京:清华大学出版社,1988.

[8] Joseph Penzien RAYW. CLOUGH.DYNAMICS OF STRUCTURES[M].New York:McGraw-Hill,1993.

[9] Hahnkamm E..Die d mpfung von fundamentschwinggungen bei veränderlicher erregerfrequenz[J].Ingenieur-Archiv,1932(4):192-201.

[10] Den Hartong J.P..Mechanical vibrations[M].New York:McGraw Hill,1956.

Optimum design for structure including TMD with complex damping subjected to earthquake

Tian Huan

(ChinaIPPRInternationalEngineeringCompanyLimited，Beijing100089,China)

The steady state responses of the two degree of freedom damping structure system including the TMD with complex damping and the main structure subjected to harmonic excitation and stationary random excitation are analyzed. The dynamic equations are established. The analytic solution for the optimum damping and frequency is obtained. The damping effect of the two degree of freedom damping structure system subjected to multiple seismic waves is analyzed. The difference of the damping effect between TMD with complex damping and TMD with viscous damping is compared. The influencing factor and the law of TMD’s damping effect are studied under different seismic wave excitations. The results showed that the vibration reduction effect of the system with complex damping is very close to the effect of the system with viscous damping. When the TMD is applied in vibration control, complex damping is an advisable option.

complex damping, TMD, harmonic excitation, white noise excitation, seismic wave excitation

1009-6825(2017)05-0042-04

2016-12-05

田 欢(1990- )，男，硕士，工程师

TU352

A