多个弹性夹杂附近半圆形凸起地形对弹性波的散射★
2017-03-29吕晓棠
吕 晓 棠
(合肥学院,安徽 合肥 230022)
·结构·抗震·
多个弹性夹杂附近半圆形凸起地形对弹性波的散射★
吕 晓 棠
(合肥学院,安徽 合肥 230022)
利用复变函数法,给出了稳态SH波作用下浅埋多个弹性夹杂附近半圆形凸起地形地表位移的求解方程,在求解区域内分别构造满足各自边界条件的波函数,通过满足弹性夹杂的边界条件得到问题的定解方程组,基于求解方程组,可以得到凸起地形表面的位移场和浅埋夹杂的应力场变化情况。
多个弹性夹杂,散射,弹性波,地震动
0 引言
一直以来,对于地震时地面运动受复杂场地条件影响的情况研究,始终是弹性波动理论研究范畴内的重要课题之一[1-3],同时,研究的成果对于抗震实践也有重要的指导意义。刘殿魁等对SH波作用下,半圆形凸起附近存在近地表圆形孔洞时凸起地表位移的变化情况展开了讨论[4]。2010年,梁建文等给出了半空间中的半圆形凸起地形对SH波散射问题的解[5]。吕晓棠对SH波作用下半圆形凸起附近的弹性夹杂的动应力情况进行了讨论[6]。本文通过分区的方法,讨论了SH波入射的情况下,当半圆形凸起附近存在弹性夹杂时的地震动问题时,所得到的结果对地面及地下结构的工程抗震具有参考意义。
1 问题的求解模型
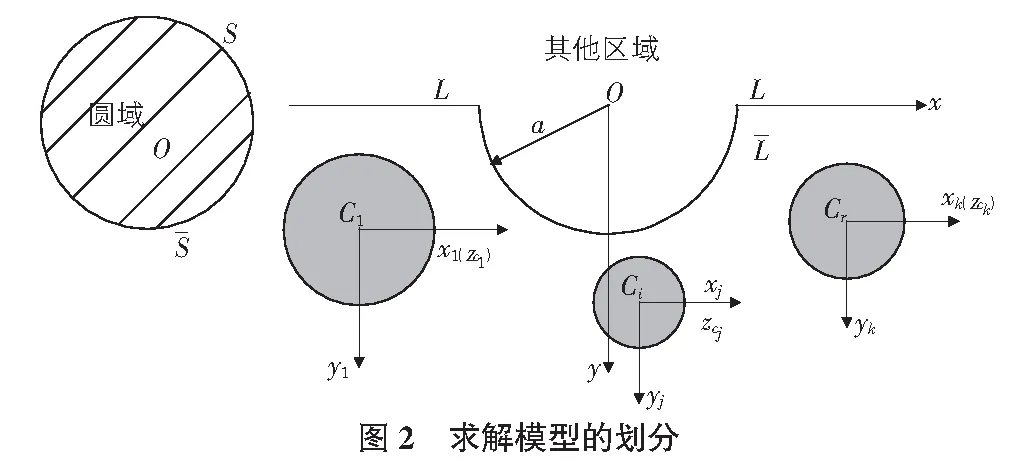
如图1所示为浅埋多个弹性夹杂附近的半圆形凸起地形的简化模型。其中,S和L分别为凸起和水平地表边界,地下有k个弹性夹杂Cj(j=1,2,…,k)。

2 问题的分析
将求解模型进行划分,分为圆形区域、其他区域和弹性夹杂区域三部分,如图2所示。
2.1 圆域中的波函数

(1)
相应的应力表达式为:

(2)
2.2 其他区域中的波函数
其他区域内的散射波W(s)要能够满足半空间表面L上应力自由这一条件。

(3)

(4)
(5)
相应的应力可分别表示为:
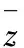
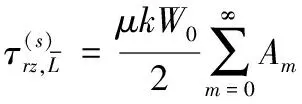
(6)
(7)
2.3 弹性夹杂Cj内的波函数
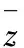

(8)
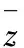
相应的应力可表示为:

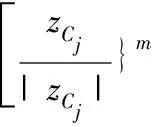
(9)
这里只写出τrz,依据极坐标下位移和应力的关系式,同理可得τθz。
3 问题的解答
3.1 入射波和反射波
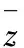

(10)

(11)
相应的应力可表示为:
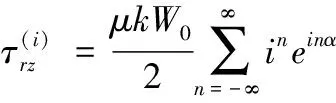

(12)
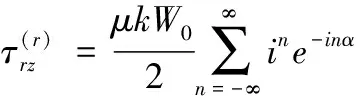

(13)
3.2 边界条件及定解方程组
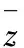
(14)
式(14)即为决定未知系数Am,Bm,Cm,Dm的无穷代数方程组。
4 结论
弹性半空间中的总波场可以写为:
(15)
方程组(14)可以通过截断有限项的方法求解。求解后,可以得到水平面上任意一个观察点上的地震动变化规律与弹性波的入射角、入射频率,夹杂的密度、间距,半径大小等变量之间的关系。对于本文所讨论的情况,在获得观察位置处的位移情况后,可以继续求解出相同位置点的加速度,为相关的抗震工程理论方面的研究提供有参考价值的数值资料。
[1] TRIFUNAC.M.D.Scattering of Plane SH-waves by a Semi-Cylindrical Canyon[J].Earthquake Engineering and Structural Dynamics,1973(1):267-281.
[2] Liu Diankui,Han Feng.Scattering of Plane SH-waves by a Cylindrical Canyon of Arbitrary Shape[J].Int.J.Soil.Dynamic and Earthquake Engineering,1991,10(5):249-255.
[3] Yuan Xiaoming,Men Fulu.Scattering of Plane SH-waves by a Semi-cylindrical Hill[J].Earthq.Eng.and Struct.Dynamics,1992(21):1091-1098.
[4] 刘殿魁,王国庆.浅埋圆形孔洞附近的半圆形凸起对SH波的散射[J].力学学报,2006,38(2):109-128.
[5] Liang Jianwen,Luo H,Lee VW.Diffraction of plane SH waves by a semi-circular cavity in half-space[J].Earthquake Science,2010,23(1):5-12.
[6] Lv Xiaotang.Dynamic analysis of an elastic cylindrical inclusion below a semi-cylindrical hill impacted by SH-wave,International journal of earthsciences and engineering,2014,7(4):1362-1369.
Scattering of elastic wave by a semi-cylindrical hill above multiple elastic inclusions★
Lv Xiaotang
(HefeiUniversity,Hefei230022,China)
The solving equation was given by the complex variable function, which can be used to study the surface motion of a semi-cylindrical hill above multiple elastic inclusions under incident SH-waves. The different wave functions were constructed to satisfy the respective boundary conditions. And the infinite algebraic equations were established according to the boundary conditions of every elastic inclusion. The numerical results of the algebraic equations can be used to describe the variation of displacement field and stress field.
multiple elastic inclusions, scattering, elastic wave, ground motion
1009-6825(2017)05-0027-02
2016-12-07★:安徽省高校自然科学研究重点项目(KJ2016A599)
吕晓棠(1975- ),女,副教授
TU311
A
