几种模型在南方地区总辐射量估算中的精度分析*

吴立峰，王 娟，张富仓，范军亮，燕 辉，鲁向晖



几种模型在南方地区总辐射量估算中的精度分析*

吴立峰1，王 娟2，张富仓3**，范军亮3，燕 辉4，鲁向晖1

（1.南昌工程学院鄱阳湖流域水工程安全与资源高效利用国家地方联合工程实验室,南昌 330099；2.扬州大学水利与能源动力工程学院，扬州 225009；3.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100；4.江西农业大学江西省鄱阳湖流域农业资源与生态重点实验室，南昌 330045）

以南方地区15个辐射站1981-2014年逐日常规气象资料和大气顶层辐射（Ra）为输入参数，以辐射站观测的逐日地表总辐射量（Rs）为对照，分别利用1981-2009年气象资料以及5种经验模型（Ångström-Presscott模型、Bahel模型、Bristow-Campbell模型、Chen模型和Hargreaves模型）和12种不同参数组合形式的广义回归神经网络（GRNN）建立Rs估算模型，并对以上模型模拟效果进行对比分析，利用2010-2014年数据对各模型模拟精度进行验证，最后采用相邻站点资料建立模型，使用本站数据评价模型的适用性。结果表明：经验模型中Chen模型精度最高，其次是Bahel模型，Bristow-Campbell模型与Hargreaves模型相比在大部分站点精度相差不大。当缺乏本地资料时，Bahel模型精度最高的站点有9个，而Chen模型最适宜的站点为7个；15个站中有13个站点B-C模型比Hargreaves模型精度更高，但在武汉站和赣州站，Hargreaves模型精度更高，其RMSE降低约14%。输入参数为日照百分比时GRNN模型的平均RMSE最低，优于Bahel和Chen模型，但其各站平均RMSE相差不足2%。当仅有本站气象资料时，GRNN模型与Bristow-Campbell模型和Hargreaves模型相比，其RMSE下降约14%，但使用邻近站点数据建模时，由于光滑因子在各站差异较大，GRNN模型与Bristow-Campbell模型和Hargreaves模型精度相差不大。因此，考虑到GRNN模型建模较复杂，故认为Bahel模型和Chen模型为南方地区更适宜的Rs估算模型。

地表总辐射；广义回归神经网络(GRNN)；Bahel模型；Chen模型；日照时数

地表总辐射（Rs）是潜在蒸散量估算[1-2]，作物产量预报[3]，太阳能开发利用[4]，气候变化研究[5]等领域重要的基础数据，获得精确的Rs对于以上领域都有重要的科学意义。Rs观测设备昂贵且需大量维护和校正[6-7]，中国仅设置了100余个太阳辐射量观测台，其中具备较完整的长时间序列资料且仍在运行的观测台不足60个，尽管经过非常严格的质量控制，有观测条件的Rs数据在时间序列上也并不完整，数据缺失现象仍普遍存在，现有的实测数据已经难以满足科研与实际应用的需要[7]。

通过常规气象资料估算Rs的方法是解决辐射数据不完整的主要方法，如基于卫星图片的分析方法[8]、人工神经网络方法[9]、基于经验系数[10-11]的模型法等，其中Ångström-Presscott模型（A-P模型）由于其结构简单且精度较高在中国得到了广泛的研究，是目前主要采用的方法[12]。Liu等[11]评估了不同时间尺度下A-P模型的精度，发现日尺度和月尺度的模型精度是等效的；有学者还建立了A-P模型与空间信息的关系[12-13]。与A-P模型结构相似，Bahel也仅需日照资料，但其精度要高于A-P模型[14]。尽管基于日照时数的辐射模型精度很高，但日照时数数据并不像气温数据那样容易获取。基于此，Bristow等[15]建立了以日最高最低气温差为输入变量的总辐射估算模型；Hargreaves等[16]在估算参考作物蒸散量时，建立了基于日气温差估算Rs的方法。Chen等[17]比较了A-P、Bahel、Bristow-Campbell、Allen和Hargreaves 共5种经验辐射模型在中国的适用性，还提出了精度更高的基于日照时数和气温资料的Chen模型。刘可群等[18]设计了利用日照百分比率、降水量与大气可降水量和温度日较差等因子推求太阳总辐射的模型，其精度高于传统经验模型。但也有不少研究发现改进的经验辐射模型并不总是能够提高模型的精度[19-21]。

此外，由于不同地区数据资料完整程度不同，经验模型难以满足各地不同的需求，人工智能方法由于输入参数组合灵活，是Rs估算方面较有前景的方法，相比传统经验模型参数组合形式更为灵活。Olatomiwa等[22]使用气温和日照时数等信息建立了自适应模糊推理系统（ANFIS）来估算尼日利亚的Rs。Cao等[23]使用神经网络与小波分析耦合来预测Rs的时间序列。Rehman等[24]基于径向基神经网络使 用日期、气温和相对湿度数据建立了沙特阿拉伯的总辐射和漫射预报模型，并给出了最适宜的模型参数。Lбpez等[25]使用风速、相对湿度、气温和土壤温度建立了小时尺度的智利Rs估算模型。Celik等[26]使用广义回归神经网络（GRNN）预测土耳其伊斯肯德仑地区坡地的Rs，输入参数包括地表总辐射、赤纬和时角，其R2达到0.987，MAPE为14.9Wh·m-2。Wang 等[27]评估了多层感知器神经网络（MLP）、GRNN、径向基函数神经网络（RBNN）在中国12站点的适用性，发现MLP和 RBNN的RMSE（1.94～3.27和1.96～3.25MJ·m-2·d-1）稍低于GRNN（2～3.29MJ·m-2·d-1），但GRNN也具有训练速度快，不需要设置神经元个数的优势。

尽管已有报道显示，GRNN模型在预测精度方面高于传统经验模型，但适宜的参数取值方面各地差异很大，选取一种数据要求低，结构简单且精度较高的适宜南方地区的Rs估算模型对实际应用有重要意义。因此，本文拟以日照时数、气温、相对湿度和降雨量的12种不同组合方式为输入变量，建立基于GRNN的中国南方地区模拟模型，并进行模型参数优化，将模拟结果与基于日照时数和基于温度的5种经验辐射模型进行比较，最后以相邻站点气象资料建模互相验证模型的可靠性，探寻中国南方地区不同气象要素条件下适宜的Rs预报模型，以期 为Rs的精确估算提供参考。

1 资料与方法

1.1 试验区概况

选取南方地区15个具有长系列观测资料的辐射站作为研究对象，站点分别位于湖北、安徽、江苏、河南、贵州、广西、广东、江西、浙江、福建和海南11个省级行政区（20.02-32.00°N，106.43- 120.1.00°E），海拔4.2-1074.3m。

1.2 数据来源

日气象资料包括日总辐射量（Rs）、日照时数（n）、20：00-20：00降水量（P）、最高气温（Tmax）、最低气温（Tmin）和相对湿度（RH），数据来源于中国气象科学数据共享服务网地面观测数据中的日值数据集，辐射数据来自中国气象辐射基本要素日值数据集2.0版。各站基本情况见表1。气象数据分为两部分，其中1981-2009年数据用于经验模型的参数率定（GRNN训练），2010-2014年数据用于模型验证。数据均经过严格的质量控制，剔除质量控制码不为0（非完全正确的数据），此外，还对气象资料进行了如下处理：（1）当每日气象资料有一项及以上数据缺失，则删除该日全部数据；（2）当地表总辐射（Rs）>地外总辐射（Ra）或实际日照时数（n）>该日理论最大日照时数（N）时，则删除该日全部数据[10]。

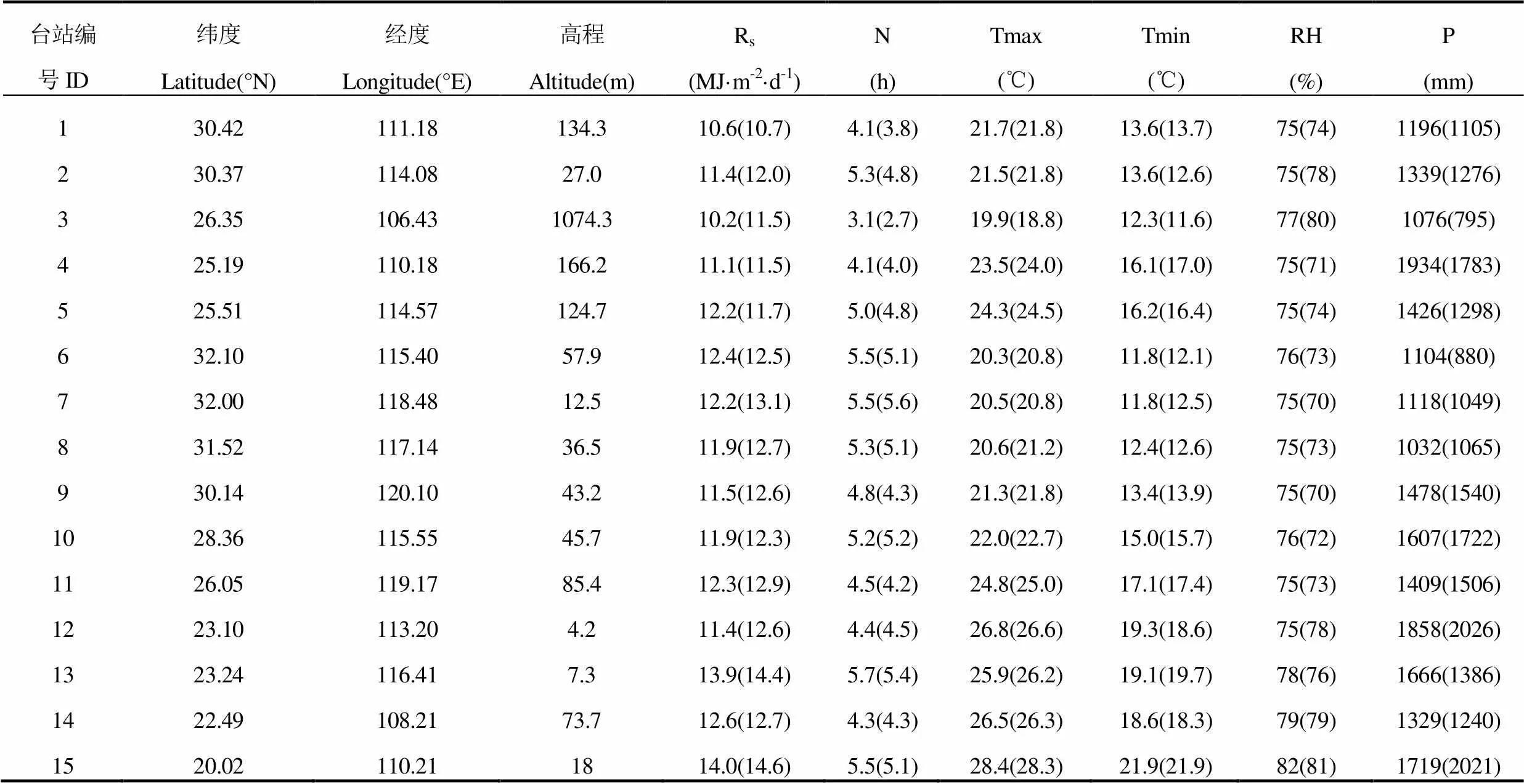
表1 15个辐射站的基本数据（1981-2009年，2010-2014年）

注：Rs为地表总辐射，n为日照时数，Tmax为日平均最高气温，Tmin为日平均最低气温，RH为日平均空气相对湿度，P为年降水量平均值。括号外为1981-2009年数据，括号内为2010-2014年数据。编号1-15分别代表宜昌、武汉、桂林、赣州、固始、南京、合肥、杭州、南昌、福州、广州、汕头、南宁和海口站。下同。

Note：Rs is global solar radiation, n is the average value of daily solar hour duration, Tmax and Tmin are the average of daily maximum and minimum air temperature, RH is the average value of daily relative humility, P is the average annual precipitation. Data period outside brackets is 1981-2009, data period in brackets is 2014-2014.ID 1-15 mean Yichang, Wuhan, Guilin, Ganzhou, Gushi, Nanjing, Hefei, Hangzhou, Nanchang, Fuzhou, Guangzhou, Shantou and Haikou stations, respectively. The same as below.

1.3 研究方法

1.3.1 经验模型

Ångström-Presscott模型[9]、Bahel模型（Bahel）[14]、Bristow-Campbell模型（B-C）[15]、Chen模型[17]和Hargreaves模型（Harg）[16]5个模型是分别利用日照时数或气温日较差的实际观测资料，在某个特定区域获得相应的经验系数后形成的Rs估算模型，是中国较常用的Rs估算模型。本文利用基于南方地区15个站1981-2009年逐日辐射实测资料，采用最小二乘法拟合得到各模型的经验系数，并通过回代和对2010-2014年进行模拟计算，与实测值进行比较验证，分析各模型在当地的适用性。

Ångstrom-Prescott（A-P）计算式为

Bahel模型计算式为

Bristow-Campbell模型计算式为

Chen模型计算式为

Hargreaves模型（Harg）

式中，n为日照时数（h），N为最大可能日照时数（h），ΔT为气温日较差（℃），Ra为大气层顶部所接收的太阳辐射量（MJ·m-2·d-1)，其计算参考文献[8]。各式中a、b、c、d为拟合后的经验系数。

1.3.2 广义回归神经网络模型（GRNN）

Specht[28]首先提出广义回归神经网络模型（GRNN），该模型是径向基神经网络的一种形式。与传统BP神经网络不同，GRNN在逼近能力和学习速度方面比径向基神经网络具有更强的优势[29]。GRNN由4层构成，分别是输入层、模式层、求和层和输出层。输入层节点个数等于评价指标个数，实现输入向量的转置；模式层节点个数一般等于或稍少于训练样本个数，实现高斯径向基函数变换；求和层一般有两个节点，实现模式层函数值与权重的点积；输出层一般只有1个节点，可表示为[29]

表2 GRNN模型输入变量的多种组合

注：N为最大可能日照时数（h）。

Note: N is the maximum solar hour duration (h).

1.4 模型评价与数据处理

经验辐射模型采用最小二乘法拟合，使用MATLAB 2014a的lsqcurvefit函数实现，使用newgrnn函数实现GRNN算法，拉丁超立方抽样使用R语言[31]中lhs包的randomLHS函数实现。

对实测值与模拟值进行对比分析，验证模型使用两个评价指标：均方根误差（RMSE）[8]表示模拟值与实测值的误差，决定系数（R2）[8]表示模拟值与实测值的一致性。

2 结果与分析

2.1 经验模型及模拟结果

利用15个站点1981-2009年逐日实测资料拟合得到各模型的经验系数见表3。由表可见，A-P模型参数b的变化范围为0.52～0.61，CV为0.04，其各站变异较小，参数a表示在云层全部遮盖时到达地面日总最小辐射量占大气层顶部所接收的太阳辐射量Ra的比例，其值在0.12～0.17，CV为0.11，a+b表示完全晴空时到达地面日最大总辐射量占Ra的比例，其值在0.66～0.75，CV仅0.03。Bahel模型参数a与A-P模型的物理意义相同，值低于A-P模型参数a约0.02，参数b在1.05～1.41，CV也较小，为0.07，由于模型中n·N-1为介于0～1的数，对Bahel模型影响最大，参数c和d为调节项，可修正一次项估值过高或过低引起的偏差，CV在0.13和0.15，变异性较强。Bristow-Campbell模型参数a也可以表示完全晴空时到达地面日最大总辐射量占Ra的比例，其值在0.52～0.60，CV为0.04，变异性较小，该值明显低于A-P模型对应值（参数b）。Chen模型参数无明确物理意义，a在0.42～0.50，CV为0.06，变异性也较小；参数b和c可以看作是修正系数，CV大于 0.25，在各站变异性较强。Harg模型参数a在0.24～0.28，CV为0.08，该模型为FAO56在日照资料缺乏时的替代方法，并推荐内陆地区参数取值0.16，沿海地区0.19[32]，研究区域明显高于该推荐值。

对2010-2014年数据进行模拟计算并与实测值比较，结果见表4。由表可见，总体上看，15个站点中，A-P模型模拟值与实测值一致性（R2）均较高，在0.753（固始）～0.937（南京），RMSE相对较低，在2.01～4.45MJ·m-2·d-1，R2在0.8以下的仅杭州和固始2站，RMSE值也相对较高；Bahel模型模拟值与实测值数据系列间的R2均较高，在0.766～0.949，RMSE相对较低，在1.86～4.31MJ·m-2·d-1，R2在0.8 以下的仅固始站，RMSE值略低于A-P模型结果；Chen模型模拟值与实测值一致性（R2）均较高，在0.764～0.945，RMSE相对较低，在1.82～4.18MJ·m-2·d-1，R2在0.8以下的仅固始站，RMSE值与Bahel模型结果相差不大；B-C模型和Harg模型R2均较低，分别在0.560～0.736和0.533～0.746，RMSE也较高，分别在3.56～5.57MJ·m-2·d-1和3.62～5.20MJ·m-2·d-1。说明A-P模型、Bahel模型和Chen模型在本文所选南方地区各站点模拟R2的普适性均较强，B-C模型和Harg模型在各站点模拟效果不佳。进一步以各站R2最高或次高、RMSE值最低或次低为条件，依次选择各站模拟效果最优的经验模型（表4中以*标注），结果显示，武汉、桂林、固始、南京、海口站以Bahel模型的模拟效果最好，其它站点均以Chen模型的模拟效果最好，占总站数的66.7%；此外，15个站Chen模型的RMSE平均比A-P模型和Bahel模型低7.6%和1.6%，可见，Chen模型是整体上适应性最好的方法。

2.2 GRNN模型及其模拟结果

GRNN模型中，光滑因子能够决定隐含层基函数的形状，取值范围通常在0～2。为了获取每个站点在每种输入组合中的最佳光滑因子值，首先建立光滑因子与RMSE的关系曲线：在0～2区间内以0.02为间距进行100次抽样，然后利用1980-2009年数据得到所有站点每种输入组合中光滑因子取值与RMSE的关系曲线。结果显示所有站点两者关系曲线均具有相同的特点，因此限于篇幅，图1仅给出宜昌站的结果。由图1可以看出，在0～2区间内，GRNN1、GRNN2、GRNN5、GRNN6、GRNN7、GRNN8模型表现为RMSE随光滑因子取值增大先降低后升高的态势，且RMSE最小时的光滑因子均较小（＜0.25），这些模型的共同点为输入参数中均包含n/N。当模型输入资料组合中包含温度项时如GRNN3、GRNN4、GRNN9、GRNN10、GRNN11和GRNN12，曲线变化更平缓，其中GRNN3模型的RMSE对σ值不敏感，其它曲线在RMSE达到最低时，σ值相比输入参数中均包含n/N的模型也更大。产生这种现象的原因可能是由于n/N的值在0～1，且在南方阴雨天0值较多，因此，不同气象日数值变化非常剧烈，而温度日较差波动相对更平缓，所以造成了前者的σ值更小，当更小的σ值作为分母时，可以获得更广泛的模拟结果输出范围。从以上分析可以看出，仅有气温日较差作为输入变量时，光滑因子取值选取默认值，但精度较低；当输入变量含有其它气象因子时，光滑因子取值有必要进行优化。

表3 各站点经验模型中系数的模拟结果（1981-2009年）

注：A-P为Ångstrom-Prescott模型，Bahel为Bahel模型，B-C为Bristow-Campbell模型，Chen为Chen模型，Harg为Hargreaves模型。Max为最大值，Min为最小值，CV为变异系数。下同。

Note: A-P is Ångstrom-Prescott model. Bahel is Bahel model. B-C is Bristow-Campbell model. Chen is Chen model. Harg is Hargreaves model. Max is maximum value. Min is minimum value. CV is coefficient of variance. The same as below.

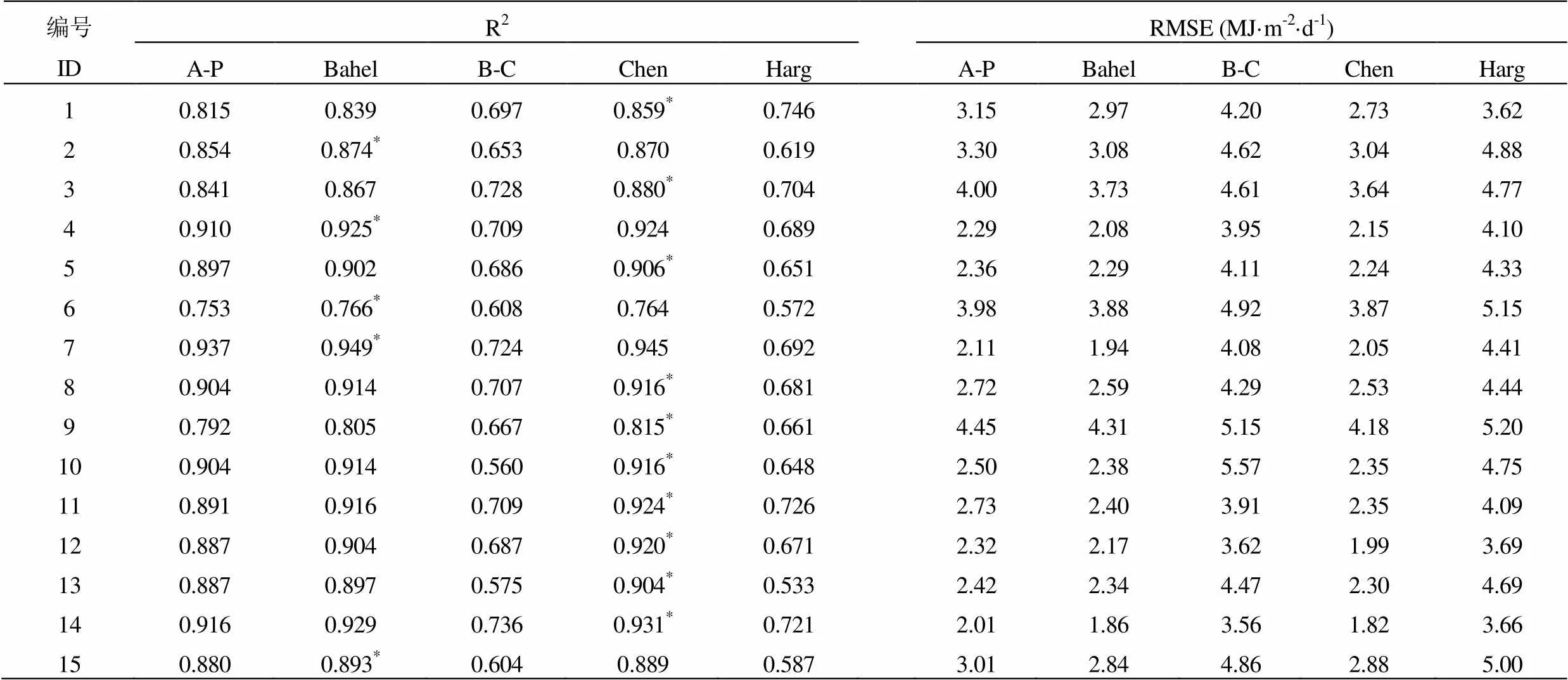
表4 各站点经验模型模拟值与实测值间的决定系数（R2）和均方根误差(RMSE)（2010-2014年）

注：*表示以各站R2最高或次高、RMSE值最低或次低为条件，选择各站模拟效果最优的结果。下同。

Note:*means the optimal result at each station selected by the rules of highest or second-highest R2and lowest or second-lowest RMSE. The same as below.

使用拉丁超立方在0～2范围内对σ值进行300次拉丁超立方抽样，然后分别进行GRNN训练和预报，选取预报值与实测值RMSE最低的模型作为各站的GRNN预报模型，并与σ值为默认值1时相对应的GRNN进行比较。各站默认值和优化后取值GRNN的R2和RMSE各站平均值如图2所示，从图可以看出，优化σ值与默认值相比对GRNN3、GRNN4、GRNN9-12的R2和RMSE各站平均值影响很小。而GRNN1、GRNN2、GRNN5-8在优化σ后，RMSE下降24%～56%，其中GRNN1的验证精度提升幅度最大。进一步说明，GRNN的光滑因子σ本地化是十分必要的。

利用2010-2014年资料代入GRNN各模型进行验证，σ值以及预报值与模拟值的R2、RMSE计算结果如表5所示。从表中可以看出，输入参数中均包含n/N，且RMSE最小时模型的σ值都较小，且各站差异很小；如GRNN1和GRNN2模型可以考虑整个区域所有站点使用相同的σ值（如0.005），替代站点与本站点σ值的空间差异可能对模型精度影响较小。而输入参数包含温度资料时，σ值变化幅度较大，其中变化幅度最大的为GRNN3模型（σ值在0.100～1.111），当采用其它站点数据建模时，可能会对模型的预测精度造成一定影响。

当输入参数只有一种时，15个站点中，GRNN1和GRNN2模型模拟值与实测值的一致性（R2）相近，均在0.767（固始）～0.951（南京），RMSE相对较低，在1.81～4.30MJ·m-2·d-1，R2在0.8以下的仅固始站，RMSE较高；GRNN3模型模拟值与实测值一致性（R2）较低，在0.578～0.771，RMSE也较高，GRNN4模型模拟值与实测值一致性（R2）也较差，在0.635～0.796，稍好于GRNN3模型。

由以上可知，当输入参数仅一种时，各模型精度表现为GRNN1=GRNN2＞GRNN4＞GRNN3，说明初等函数形式对GRNN模型的影响较小，而输入参数为最高和最低气温2个变量时模型精度要好于仅输入气温日较差一个参数。

表5 GRNN验证期实测值与模拟值的R2和RMSE（2010-2014年）

当输入变量含2种不同类型气象资料时，在5种模型（GRNN5、GRNN6、GRNN7、GRNN11和GRNN12）中，GRNN11和GRNN12模型模拟值与实测值一致性（R2）均较低，分别在0.648（固始）～0.835（福州）和0.663（固始）～0.817（福州），RMSE较高，在3.01～4.77MJ·m-2·d-1和3.10～4.59MJ·m-2·d-1；GRNN5模型模拟值与实测值一致性（R2）较低，在0.724（固始）～0.891（福州），RMSE也较高，在2.32～4.24MJ·m-2·d-1；GRNN6模型模拟值与实测值的一致性（R2）最好，在0.767（固始）～0.947（南京），RMSE最低，在1.78～3.84MJ·m-2·d-1；GRNN7模型模拟值与实测值的一致性（R2）较好，在0.757（固始）～0.937（南京），RMSE较低，在2.12～4.33MJ·m-2·d-1。

当输入变量含3种不同类型气象资料时，GRNN8和GRNN10模型精度均较差，R2分别0.714（固始）～0.880（南京）和0.658（固始）和0.814（福州），RMSE也较高，分别在2.67～4.37MJ·m-2·d-1和3.06～4.70MJ·m-2·d-1，其中GRNN8与GRNN6和GRNN7相比增加了气象资料，但精度却明显低于后两者。可见，增加气象资料并不能明显提高甚至还可能降低GRNN模型的精度。

当输入变量含4种不同类型气象资料时，GRNN9模型的精度也较差，R2分别在0.666（固始）～0.821（福州），RMSE也较高，在3.00～4.64MJ·m-2·d-1。进一步说明GRNN模型增加气象资料的类型会降低模型精度。

进一步以各站R2最高或次高、RMSE值最低或次低为条件，依次选择各站模拟效果最优的经验模型（表中以*标注），结果显示，宜昌、贵阳、合肥、杭州、南宁和海口站GRNN6模型的模拟效果最好，其它站点均以GRNN1模型的模拟效果最好，占总站数的66.7%。此外，15个站GRNN1模型的RMSE平均也最低，是模拟精度最高的GRNN模型。

2.3 几种模型对同一站点模拟结果的综合比较

为了进一步比较经验模型和GRNN模型的精度，分别选取经验模型和GRNN模型中相同输入变量下的各辐射模型进行比较，结果如图3所示。从图3a可以看出，当输入变量仅有日照时数资料时，与Bahel模型相比，GRNN2在各站RMSE平均下降仅0.3%，精度提高很小。与Chen模型相比，GRNN5各站的RMSE均更高，平均提高12.0%（图3b）；当输入变量仅有气温资料时，GRNN4的RMSE在各站较小，与B-C模型和Harg模型相比RMSE分别平均下降10.7%和12.2%（图3c）。从以上可以看出，当输入资料包含日照资料时，经验模型是该地区更适宜的总辐射预测模型，而当仅有气温资料时，GRNN模型可以提高当地的总辐射预测精度。

2.4 几种模型对相邻站点模拟结果的比较

由于Rs数据难以获取，通常需要周边的Rs资料来预报本地的Rs值。因此，跨站模拟精度更高的模型更具有应用价值。本研究在本地资料建模基础上，对邻近站点Rs进行预报，并比较各模型的预报精度，结果见表6和表7。可以看出，当无本地Rs观测条件时，使用相近站点的经验模型参数后，A-P模型、Bahel模型和Chen模型验证结果的RMSE与原站点气象数据建立辐射模型的RMSE（表4）相差很小。而B-C模型和Harg模型RMSE提高幅度较大，分别平均提高12.0%和9.2%，尽管B-C模型的各站RMSE均值高于Harg模型，这主要是由于B-C模型在个别站点（如站1和站10）误差远大于Harg模型，提高了RMSE的平均值。虽如前文（2.1）所述，Chen模型稍好于Bahel模型，但在缺乏本地资料时，Bahel模型稍好于Chen模型，在9个站点的RMSE均最低，Chen模型仅7个。可见A-P模型、Bahel模型和Chen模型在南方地区泛化能力较强，特别是Bahel模型，尽管本地化参数较多，但预报精度在邻近站点也有稳定的表现。

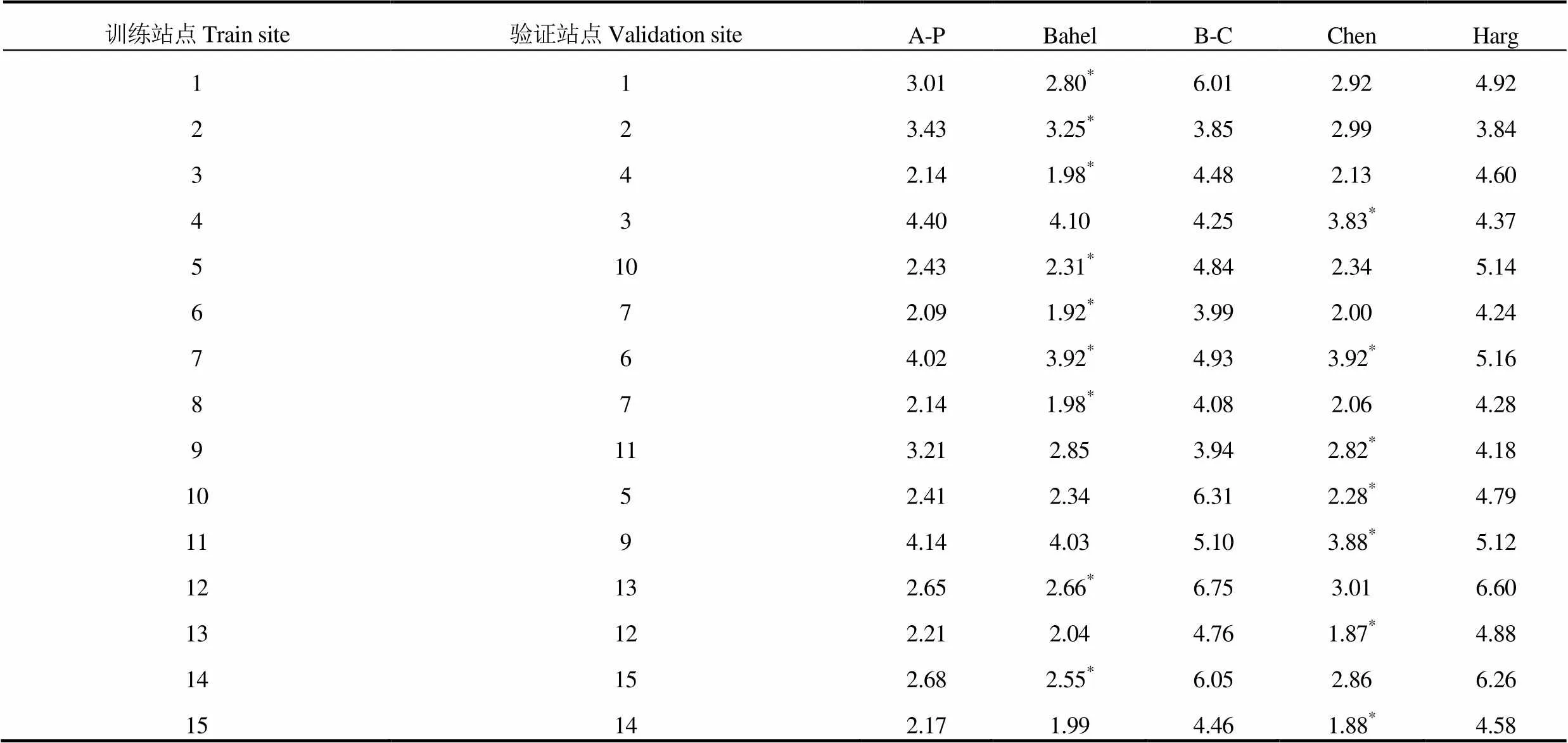
表6 训练数据和验证数据来自不同站点时经验辐射模型模拟结果的RMSE（2010-2014年）

表7 训练数据和验证数据来自不同站点时GRNN模型模拟结果的RMSE（2010-2014年）

从表6可以看出，GRNN模型的泛化能力随输入参数组合形式不同表现出很大差异。当本地无Rs观测条件时，使用相近站点的资料建立GRNN模型后，GRNN1、GRNN2、GRNN6和GRNN7模型RMSE变化很小，而其它GRNN模型的RMSE提高幅度较大，均在11%以上。这可能是由于GRNN1、GRNN2、GRNN6和GRNN7模型光滑因子在各站差异很小，可以直接替换到其它站点而精度变化很小，而其它GRNN模型的光滑因子在各站差异很大，导致泛化能力较差。对比Bahel、Chen和GRNN1模型可以看出（表6和表7），GRNN2模型在各站RMSE均更低，但下降幅度与Bahel和Chen模型相比很小，最大仅为2%左右。

3结论与讨论

（1）在南方15个辐射站中，当使用本站资料率定和验证模型时，Chen模型精度最高，R2在0.764～0.945，RMSE在1.82～4.18MJ·m-2·d-1，Bahel模型总体上精度略低于Chen模型，各站平均RMSE比Bahel模型低1.6%，A-P模型精度排第三位，这与Chen等[17]的研究结论相似。B-C模型与Harg模型精度均较差，在南昌站和宜昌站Harg模型精度更高，而其它站B-C模型稍好于Harg模型，造成这种现象的原因可能是B-C模型与Harg模型相比多一个参数，而且前者的参数b为指数参数且取值大于1，可以用来增大气温日较差对整体值的影响；而Harg模型的温度日较差使用了0.5次方形式，降低了气温日较差对总辐射量的影响。

（2）当缺乏本地资料时，需要使用邻近站点建立经验辐射模型，Bahel模型精度稍好于Chen模型，且RMSE最低的站点有9个，多于Chen模型（7个）。15个站中有13个站点B-C模型比Harg模型精度更高，但在武汉站和赣州站，Harg模型精度更高，RMSE下降约14%。需要指出的是，本研究中的同组站点是在研究区内15个站点中选取，带有一定的主观性，可能有精度更高的替代站点，精度也有进一步提高的空间，这方面还有待进一步研究。

（3）15个站GRNN1模型的平均RMSE值也最低，是模拟精度最高的GRNN模型。增加气象资料并不能明显提高GRNN模型精度，甚至会降低模型精度，不同站点光滑因子差异较大是造成GRNN模型在相邻站点精度下降明显的主要原因。Wang等[27]比较了改进B-C模型和GRNN在全国12个站点的精度，发现GRNN比改进B-C模型精度更高。但本研究中，与Bahel模型相比，尽管GRNN1模型在各站RMSE均更低，但RMSE下降幅度很小，最大仅为2%左右。所以，考虑到GRNN模型建模较复杂，精度也无明显的提升，建议在南方地区使用Bahel模型和Chen模型进行辐射量估算。

[1]冯禹,崔宁博,龚道枝.机器学习算法和Hargreaves模型在四川盆地ET0计算中的比较[J].中国农业气象, 2016, 37(4): 415-421.

Feng Y, Cui N B, Gong D Z.Comparison of machine learning algorithms and Hargreaves model for reference evapotranspiration eestimation in Sichuan basin[J].Chinese Journal of Agrometeorology, 2016, 37(4):415-421.(in Chinese)

[2]Allen R G,Pruitt W O,Wright J L,et al.A recommendation on standardized surface resistance for hourly calculation of reference ET0by the FAO56 Penman-Monteith method[J]. Agricultural Water Management,2006, 81(1-2): 1-22.

[3]Porter J R.AFRCWHEAT2:a model of the growth and development of wheat incorporating responses to water and nitrogen[J].Europe Journal Agronomy, 1993(2):69-82.

[4]Li H S,Ma W B,Lian Y W,et al.Estimating daily global solar radiation by day of year in China[J]. Applied Energy, 2010, 87(10):3011-3017.

[5]Susan S,James L,Philip A,et al.Solar radiation management could be a game changer[J].Nature Climate Change, 2014, 4(10):842-842.

[6]Hakuba M Z,Folini D,Schaepman-Strub G,et al.Solar absorption over Europe from collocated surface and satellite observations[J].Journal of Geophysical Research Atmospheres, 2014,119(119):3420-3437.

[7]Şahin M,Kaya Y,Uyar M.Comparison of ANN and MLR models for estimating solar radiation in Turkey using NOAA/AVHRR data[J].Advances in Space Research, 2013, 51(5):891-904.

[8]Liu X,Mei X,Li Y,et al.Evaluation of temperature- based global solar radiation models in China[J]. Agricultural & Forest Meteorology, 2009, 149(9): 1433-1446.

[9]Liu X,Mei X,Li Y,et al.Calibration of the Ångström–Prescott coefficients (a, b) under different time scales and their impacts in estimating global solar radiation in the Yellow River basin[J]. Agricultural & Forest Meteorology, 2009,149(3-4): 697-710.

[10]Yao W,Li Z,Wang Y,et al.Evaluation of global solar radiation models for Shanghai, China[J].Energy Conversion & Management,2014,84:597-612.

[11]Liu X,Mei X,Li Y,et al.Choice of the Ångström– Prescott coefficients:are time-dependent ones better than fixed ones in modeling global solar irradiance [J].Energy Conversion & Management, 2010,51(12): 2565-2574.

[12]Liu X,Li Y,Zhong X,et al.Towards increasing availability of the Angstrom-Prescott radiation parameters across China:spatial trend and modeling[J].Energy Conversion & Management,2014,87:975-989.

[13]李曼曼,梅旭荣,钟秀丽,等.云南省Ångström- prescott 辐射模型的参数化研究[J].农业工程学报, 2012,28(6):1100-105.

Li M M,Mei X R,Zhong X L,et al.Parameterization of Ångström-prescott radiation model in Yunnan province[J]. Transactions of the CSAE,2012, 28(6): 100- 105.(in Chinese)

[14]毛洋洋,赵艳霞,张祎,等.五个常见日太阳总辐射模型在华北地区的有效性验证及分析[J].中国农业气象,2016,37(5):520-530.

Mao Y Y,Zhao Y X,Zhang W,et al.Validation and analysis of five general daily solar radiation estimation models used in northern China[J].Chinese Journal of Agrometeor- ology,2016,37(5):520-530.(in Chinese)

[15]Bristow K L,Campbell G S.On the relationship between incoming solar radiation and daily maximum and minimum temperature [J]. Agricultural & Forest Meteorology, 1984, 31(2): 159-166.

[16]Hargreaves G H.The 1980-1981 food and climate review[M].The Food and Climate Forum,Aspen Institute for Humanistic Studies,Boulder,Colo,1981:29-32.

[17]Chen R S,Yang J P,Zhao W Z.Validation of five global radiation models with measured daily data in China[J]. Energy Conversion and Management, 2004, 45: 1759-1769.

[18]刘可群, 陈正洪,梁益同,等.日太阳总辐射推算模型[J].中国农业气象, 2008,29(1):16-19.

Liu K Q,Chen Z H,Liang Y T,et al.Calculation model for daily global solar radiation[J].Chinese Journal of Agrome- teorology,2008,29(1):16-19.(in Chinese)

[19]Ball R A,Purcell L C,Carey S K.Evaluation of solar radiation prediction models in North America [J]. Agronomy Journal,2004,96:391-397.

[20]Chen J L,Li G S.Estimation of monthly average daily solar radiation from measured meteorological data in Yangtze River Basin in China[J]. International Journal of Climatology, 2013,33(2): 487-498.

[21]Wu G,Liu Y,Wang T.Methods and strategy for modeling daily global solar radiation with measured meteorological data :a case study in Nanchang station,China[J].Energy Conversion & Management,2007,48(9):2447-2452.

[22]Olatomiwa L,Mekhilef S,Shamshirband S,et al.Adaptive neuro-fuzzy approach for solar radiation prediction in Nigeria[J].Renewable & Sustainable Energy Reviews,2015,51:1784-1791.

[23]Cao S,Cao J.Forecast of solar irradiance using recurrent neural networks combined with wavelet analysis[J]. Applied Thermal Engineering, 2005,25(2-3): 161-172.

[24]Rehman S.Solar radiation over Saudi Arabia and comparisons with empirical models[J]. Energy, 1998, 23 (12):1077-1082.

[25]López G,Batlles F J,Tovar-Pescador J.Selection of input parameters to model direct solar irradiance by using artificial neural networks[J]. Energy,2005, 30(9):1675-1684.

[26]Celik A N,Muneer T.Neural network based method for conversion of solar radiation data[J].Energy Conversion & Management,2013,67(1):117-124.

[27]Wang L,Kisi O,Zounematkermani M,et al.Solar radiation prediction using different techniques: model evaluation and comparison[J].Renewable & Sustainable Energy Reviews, 2016,61:384-397.

[28]Specht D F.The general regression neural network:rediscovered[J]. Neural Networks,1993,6(7): 1033-1034.

[29]杨彬,贺正洪.一种GRNN神经网络的高超声速飞行器轨迹预测方法[J].计算机应用与软件, 2015, 32(7): 239-243.

Yang B, He Z H.Hypersonic vehicle track prediction based on GRNN[J].Computer Applications and Software,2015, 32(7): 239-243.(in Chinese)

[30]Helton J C,Davis F J.Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems

[J] Reliability Engineering System Safety, 2002,81 (1): 23-69.

[31]Core Team R.R:a language and environment for statistical computing[Z].R Foundation for Statistical Computing, Vienna, Austria, URL. https://www.R-project.org/,2015.

[32]Allan R G,Pereira L S,Raes D,et al.Crop evapotranspiration: guidelines for computing crop water requirements [J].Rome: FAO,1998:56.

Accuracy Analysis of Several Global Solar Radiation Models Based on Empirical and GRNN Methods in South China

WU Li-feng1, WANG Juan2, ZHANG Fu-cang3, FAN Jun-liang3, YAN Hui4, LU Xiang-hui1

(1.State-province United Engineering Laboratory on Water Engineering Safety and Resources Efficient Utilization of Poyang Lake basin, Nanchang Institute of Technology，Nanchang 330099, China; 2. School of Hydraulic, Energy and Power Engineering, Yangzhou University, Yangzhou 225009;3.Key Laboratory of Agricultural Soil and Water Engineering in Arid and Semiarid Area Ministry of Education, Northwest A&F University, Yangling 712100; 4. Key Laboratory of Poyang Lake Basin Agricultural Resources and Ecology of Jiangxi Province, Jiangxi Agricultural University, Nanchang 330045)

Validation of global radiation models with measured daily data based on the meteorological data (including the extraterrestrial radiation) from 15 radiation stations in South China during 1981-2009.The daily global solar radiation was estimated using five empirical models (i.e., Angstrom-Presscott model, Bahel model, Bristow-Campbell model, Chen model and Hargreaves model) and 12 generalized regression neural network models (GRNN) with different input variable combinations. The performance of these global radiation models were evaluated using observed daily global solar radiation data during 2010-2014 at the 15 radiation stations. Finally, the global radiation models were developed by meteorological data from the adjacent stations, and then evaluated the applicability of these models using the observed data from the studied station. The results showed that the Chen model had the highest accuracy among the empirical models, followed by the Bahel model. The Bristow-Campbell model performed similarly to the Hargreaves model for most radiation stations. The Bahel model had the highest accuracy at 9 of 15 radiation stations when developing models by using the meteorological data from the adjacent stations, while the Chen model was most suitable for 7 stations. The Bristow-Campbell model and Hargreaves model had higher accuracy at 13 of 15 stations. But the Hargreaves model performed better at the Wuhan station and Ganzhou station, where the RMSE was decreased by about 14%. The GRNN model had the lowest average RMSE with input variable of sunshine percentage, which was better than the Bahel model and Chen model, but the difference in average RMSE at each station was less than 2%. When using the local meteorological data, the RMSE of the GRNN model was decreased by about 14% compared to that of the Bristow-Campbell model and the Hargreaves model. When using the data from the adjacent stations, the GRNN model performed similarly to the Bristow-Campbell model and the Hargreaves model due to the large differences in the smoothing factor at each station. Therefore, the Bahel model and the Chen model were considered to be more suitable for the estimation of global solar radiation in these areas considering the complexity of GRNN model development.

Global solar radiation; Generalized regression neural network (GRNN); Bahel model; Chen model; Solar duration hours

10.3969/j.issn.1000-6362.2017.03.003

2016-06-29

通讯作者：。E-mail：zhangfc@nwsuaf.edu.cn

江西省教育厅资助项目（GJJ151123）；国家高技术研究发展计划（863计划）（2011AA100504）；国家自然科学基金(51409131)；江西省科技支撑计划(20151BBF60013)

吴立峰（1985-），博士，讲师，主要从事节水灌溉理论与技术研究。E-mail：china.sw@163.com

吴立峰,王娟,张富仓,等.几种模型在南方地区总辐射量估算中的精度分析[J].中国农业气象,2017,38(3):150-162