基于改进SIFT算法的图像配准

杜以荣

（大连大学 信息工程学院，辽宁 大连 116622）

基于改进SIFT算法的图像配准

杜以荣

（大连大学 信息工程学院，辽宁 大连 116622）

对于SIFT算法即尺度不变特征变换配准方法在进行图像配准匹配率低的问题，提出了一种再SIFT算法基础上的改进的配准方法。本文主要对图像进行梯度锐化处理，使其边缘得到突出，再利用SIFT算法进行关键点提取，并对锐化后的图像进行匹配。从而完成图像配准。实验结果显示此方法比传统SIFT方法配准结果好，并且匹配率比传统SIFT算法高。

图像配准；SIFT；梯度锐化；关键点提取；匹配率

图像配准是将传感器不同、视角不同、时间不同等条件下2幅或者多幅的图像进行变换。如平移、旋转、缩放及放射等变换。图像配准技术，主要是为了实现图像的变化检测，图像的校正，图像的融合，等最为关键的步骤[1]。

传统主要图像配准方法包括基于灰度的图像配准方法[2]、基于特征的图像配准方法[3]和基于变换域的配准方法[4]。基于灰度的配准方法容易实现并且算法比较简单。但基于灰度的配准方法对于视角的变化尺度的变化较敏感抵抗非线性干扰的能力较差。基于特征图像配准方法:Harris、CCH、SIFT等算法，对于图像的非线性变形情况这些算法都能够较好的适应，其中最具有代表性的是David Lowe提出的SIFT算法。该算法不仅具有尺度不变性，旋转不变性，仿射不变性，视角不变性。而且对于目标的噪声遮挡运动等的影响也能保持较好的配准效果[5]。因此在图像配准中SIFT算法逐渐被采纳且被改进，发展出很多改进的算法：例如针对于图像具有的噪声特性的SURF[6]算法，研究者提出SIFT-OCT[7]，BFSIFT[8]等算法。在性能上进一步得到了改进。

在图像的不变特征提取方面SIFT算法有着很大的优势：SIFT算法在图像亮度变化方面，图像平移，图像旋转，图像缩放方面，也具有很好的稳定性。具有良好的不变性，针对噪声干扰和仿射变换，SIFT算法有很好的独特性，很小的物体都能产生很多的SIFT特征点，可以得到精确和快速匹配在大量的特征数据库中，但是SIFT图像配准算法并不是完美的。实验中发现，当要匹配的图像比较模糊时，利用SIFT算法提取的关键点较少，导致匹配时正确匹配率不高[9]。针对这种情况，文中提出基于SIFT的针对模糊图像匹配增强算法，首先利用增强算子对图像进行锐化处理，文中主要对图像进行梯度锐化处理，使其边缘得到突出，再利用算法进行关键点提取，并对锐化后的图像进行匹配。这样的操作使获得的关键点数量比直接利用SIFT算法有大幅度提高。

1 SIFT算法

SIFT（scale invariant feature transform，即尺度不变特征变换）算法是David G．Lowe于1999年提出，并且于2004年对SIFT特征匹配算法，进行了完善和总结。总共包括以下几个步骤：

1.1 尺度空间的形成

高斯卷积核是实现尺度变换的惟一线性核由Koendetink等人证明，所以二维图像的尺度空间可由下式表示：

式中：尺度空间由L表示，空间坐标是由（x，y）表示，尺度因子由σ表示。σ的值越小，图像则越清晰，σ越大，图像则越模糊。为了在尺度空间中，使被检测到的关键点稳定性提高，因此采用高斯差分尺度空间（DOG）。高斯差分尺度空间被定义为两个相邻尺度的高斯核差分[10]。由下列公式（2）表示：

1.2 空间极值点的检测

在高斯差分尺度空间中，为了确保都能检测到极值点在二维图像空间及尺度空间中，除最顶层和最底层的像素点之外，每一个像素点都要和同层 8个相邻点上及下两层各9个进行比较，并且来精确地确定特征点的位置和尺度通过拟和三维二次函数，精确确定特征点的尺度和位置的同时去除不稳定的边缘特征点和低对比度的特征点，来提高抗噪声的能力、增强图像配准的稳定性。

1.3 特征点方向分配

通过统计特征点的邻域像素的梯度方向的直方图来确定每个特征点的方向参数，从而保证算子具有旋转不变性。

1.4 特征点描述器的生成

在sift算法中取16*16的邻域在特征点周围，并把取得的领域化为4*4小的区域，每个小区域统计8个方向梯度，从而得到了4*4*8=128维的向量，这个向量作为此点的sift描述子。从而增强此算子的抗噪声能力。

1.5 特征匹配

对于SIFT特征向量进行匹配是根据相似性度量来进行的。常用的特征匹配方法主要有：欧式距离、马氏距离等。用欧氏距离对SIFT的特征向量进行匹配，获得SIFT的特征向量以后，首先采用k-d树[11]进行搜索，以此来查找每个特征点的近似的最近邻特征点。如果最近的距离除以次近的距离小于于某个设定的阈值在这两个特征点中，则一对特征点即为匹配点。比例阈值越小SIFT匹配点数目会减少但会更加稳定。

2 基于锐化的匹配算法

通过SIFT算法的原理和实验可以发现，SIFT算法检测到的许多关键点都是边缘点，然而由于在构造高斯金字塔的时候会将图像经过多次高斯平滑[12-13]，使得边缘点变得很平滑，如果所获取的图像本来就质量不高，直接利用SIFT算法提取关键点进行匹配，将会大大降低匹配精度[14-15]。为了提高匹配率，本文提出先对图像进行锐化处理以提高SIFT提取的关键点数，再进行匹配。

2.1 图像锐化

图像锐化的主要目的有两个：1）使模糊图像变得更清晰，使图像的边缘增强，使图像颜色变得突出，使图像质量改善从而产生更加适合于人眼识别和观察的图像2）对图像进行锐化处理之后，使目标物体边缘变得清晰，有利于图像分割，目标边缘识别，提取区域形状，识别目标区域，为图像分析与理解奠定基础。

文中对图像主要采用梯度锐化方法进行锐化。

因为锐化处理使噪声增强 （比信号还要强的增强），因此对锐化处理的图像要求有比较高的信噪比；要不然锐化之后的图像信噪比比没有锐化之前的图像信噪比还要低。

2.2 梯度锐化

基本理论：加权平均法、邻域平均法都可以使图像平滑。相反可以利用其对应的微分算法使图像锐化。微分算法主要是用来求信号的变化率，有使高频分量增强的作用，因此使图像边缘变得清晰。图像受到平均或积分运算造成了图像模糊，对图像进行逆运算如微分运算从而把图像中任何方向伸展的边缘模糊的轮廓变得清晰，从而图像变得清晰。一阶微分是通过梯度算实现图像处理的。用函数f（x，y）表示一幅图像，定义f（x，y）在点（x，y）处的梯度是一个矢量，这个梯度矢量表示为：

函数f（x，y）最大变化率方向即为图像梯度的方向，可以由以下公式G0[f（x，y）]算出梯度的幅度：

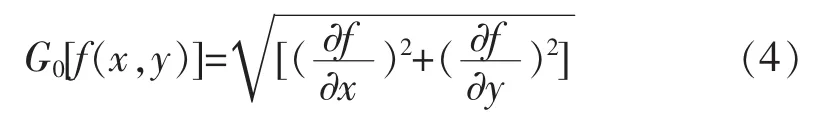
为了提高运算速度、便于编程，在计算精度允许的情况下，可采用绝对差算法表示，梯度数值可以近似表示

该算法又被称作水平垂直差分法。交叉的进行查分计算为另一种梯度算法，该算法被称为罗伯特梯度法，由以下公式表示：

同样可采用绝对差算法表示，罗伯特梯度法数值可以近似表示为：

用上述两种梯度近似算法来计算像素的梯度时，当在图像的最后一行，最后一列无法来计算像素的梯度时，一般用前一行或者前一列的值近似代替像素的梯度。

为了更好地增强图像边缘在不破坏图像背景的前提下，也可以改进以上所述用梯度值来代替灰度值的方法，可以通过引入一个阈值来判断可不可以对某一个像素点进行锐化处理。公式如下表示：

对图像来说，背景与背景之间、物体与物体之间的梯度的变化很小。集中在图像的边缘上的地方一般为灰度变化较大的地方，即背景、物体交接的地方。设定一个阈值的时候。当G0[f（i，j）]大于设定的阈值，就认为该像素点在图像的边缘。为了使边缘变亮，对结果加上常数C。当G0[f（i，j）]小于或者等于设定的阈值就认为这个像素点是同类像素，即同为同为背景或者同为物体。可以根据具体的图像特点来选取常数C。这样在增亮图像的边界的同时又保留了原来的图像背景状态，该方法对图像有更好的适用性和增强效果比传统的梯度锐化

3 本文算法

由SIFT算法的原理以及实验可以得出：边缘点都是由SIFT算法检测到的许多的关键点，因为在构造金字塔的时候会将图像经过多次高斯平滑，从而使得边缘点变得很平滑，如果所获取的图像本来就质量不高，直接利用SIFT算法提取关键点进行匹配，将会大大降低匹配精度。为了提高匹配率，文中提出先对图像进行梯度锐化处理以使SIFT提取的关键点数增多，再利用k-d树法进行匹配。

步骤如下:

将待配准的2幅图像读入，将读入的图像进行梯度锐化从而得到锐化后的图像。虽然罗伯特梯度锐化算法是近似定义计算，但罗伯特梯度锐化运算效果比较好并且简单，所以在图像处理时本文采用罗伯特梯度锐化方式，图像可以用梯度值G0[f（x，y）]来表示，可以表示为g0（x，y）=G0[f（i，j）]，由以上公式得出，当在图像变化缓慢的地方时，梯度值会很小，对应的图像则较暗，当在图像线条轮廓等变化较快的地方时，梯度值会很大。所以图像可变得清晰在经过梯度运算以后，从而图像中的对象会从原图中显出来，以达到加强景物的边缘与轮廓的目的，由此来实现图像的锐化。

设定了一个阈值Δ，当G0[f（x，y）]小于设定的阈值时，图像保持原来的灰度值不变；如果大于或等于该阈值Δ，则赋值G0[f（x，y）]为式（10）。

当在图像变化缓慢的地方时，梯度值会很小，对应的图像则较暗，当在图像线条轮廓等变化较快的地方时，梯度值会很大。所以图像可变得清晰在经过梯度运算以后，从而对边缘检测有利。对梯度锐化后的图像进行特征提取时可以利用传统的SIFT算法，并利用k-d树法对图像进行特征匹配。在特征提取的时候本文设高斯金字塔是4阶，每阶3层，利用SIFT算法对梯度锐化后的图像进行特征提取，得到2幅待匹配图像的特征集，在生成 128维的 SIFT特征描述算子后，对2个特征点进行匹配时利用欧式距离作为相似度准则 ，定义特征点对p与q的特征描述算子可以分别被表示为Desp和Desq，特征点描述子的欧氏距离被定义为下式：

查找每个特征点的两个近似最近邻特征点时，首先采用k-d树进行搜索。然后找到与特征点p的欧氏距离次近和最近的两个相邻特征点q″与q′。再计算（p，q′）和（p，q″）两组特征描述算子之间的λ即欧氏距离比，如果 λ比给定的阈值R小，则匹配成功，匹配点对 （p，q′）被接受 。文中通过大量的实验，设定的阈值为R=0.8时，得到的匹配点数最多，误匹配点数最少，匹配效果较好。采用 k-d树的数据结构来完成搜索来完成关键点的匹配，从而进行图像匹配。

通过计算两种方法的匹配时间、误匹配率、匹配率来进行比较。

4 实验结果与分析

为了验证该算法的优越性，进行了以下实验。PC（i550-2.6GHz CPU，1024MBRAM，Windows XP OS，MATLAB 6.5）的环境下进行实验。实验图像采自http：//www.nipic.com。图像特征：1图大小为26.1 kB，尺寸256*256像素 2图大小29.4 kB，尺寸256*256像素

方式1:直接利用SIFT算法提取特征对进行匹配，匹配效果图，如图1所示。

方式2:先对图像进行高斯滤波处理，再利用梯度锐化对模糊图像进行锐化处理，再利用SIFT算子对锐化后的图像提取特征并进行匹配；匹配效果图，如图2所示。

图1 传统SIFT算法图像匹配结果

图2 改进的SIFT算法图像匹配结果

通过计算两种方法的匹配点数、正确匹配点数、匹配率以及匹配时间来比较：

表1 两种算法的参数对比

由图1可以看出，在图1中匹配点数不多，所以匹配率也不高，由于对图像进行了梯度锐化，所以图2中匹配点数增多，很明显匹配率也增高。由表1可以看出改进后的SIFT算法的匹配点数、正确匹配点数以及匹配正确率都高于传统的SIFT算法。由实验结果可以得出本文的算法要好于传统的基于SIFT特征的图像匹配算法效果。

5 结束语

由于SIFT算法中要计算主方向，而主方向的计算是造成误差的一个主要原因但是本文在传统的SIFT算法的基础上，通过锐化处理和利用双向匹配算法进行特征匹配，从而减小了匹配误差，在没有改变SIFT算法本质的同时保证了匹配精度。实验结果表明本文提出的方法在提高匹配效果的同时，可以增强SIFT算子进行匹配的模糊不变性。由于本文提出的方法增加了对图像的锐化处理，进行匹配的操作，因此算法复杂度会增加，但是增加的时间复杂度相对原始算法本身的复杂度较小，所以在一定范围内可以利用本文所提出的算法进行匹配，以达到提高匹配率的目的。

文中提出的方法的运行效率比SIFT算法的运行效率低，怎样在保持高配准精度的前提下，来让运行效率提高是进行下一步的研究方向。怎样减少算法的复杂度，增加计算效率，本文匹配率增高了，但仍存在错配点，如何降低误配率。是我接下来研究的主要方向。

[1]杨晓敏，吴炜，卿粼波，等.图像特征点提取及匹配技术[J].光学精密工程，2009，17（9）:2276-2281.

[2]Mortani M，Sationh F.Image template matching based on ratio of main and central pixel in local area[J].Proceedings of the SPIE-The International Society for Optical Engineering，2007，67（94）:1-6.

[3]Barara Zitova，Jan Flusser Image registration methods: a suvery[J].Image and Vis-ion Computing，2003，21（11）:977-100.

[4]王宏力，贾万波.图像匹配算法研究综述[J].计算机技术与应用，2008（6）:17-19.

[5]LOWE D G.Distinctive image features from scaleinvariant keypoints[J].Int.J.Comput.Vis，2004，60（2）:91-110.

[6]阳及斌，胡访宇，朱高.基于改进SURF算法的遥感图像配准[J].电子测量技术，2012，35（3）:69-72.

[7]Schwind P，Suri S，Reinartz P.et al.Applicability of the SIFT operator for geometrical SAR image registration [J].Int.J.Remote Sens，2010，31（8）: 1959-1980.

[8]Wang S，You H，Fu K.BFSIFT:A novel method to find feature matches for SAR image registration [J].IEEE Geosci.Remote Sens.Lett，2006，3（3）: 354-358.

[9]曹娟，李兴玮，林伟廷，等，SIFT特征匹配算法改进研究[J].系统仿真学报，2010，22（11）:2760-2763.

[10]Lindeberg T.Scale-space theory:a basic tool for analyzing structures at different scales[J].Journal of Applied Statistics，1994，21（2）:225-270.

[11]Bentley J L.Multidimensional binary search trees used for associative searching[J].Communications of the ACM，1975，18（9）:509-517.

[12]Bastanlar Y，Temizel A，Yardmc Y.Improved SIFT matching for image pairs with scale difference[J].Electronics Letters 2010，46（5）:346-348.

[13]Schwind P，Suri S，Reinartz P.et al.Applicability of the SIFT operator for geometrical SAR image registration[J].Int.J.Remote Sens，2010，31（8）: 1959-1980.

[14]王晓华，傅卫平，梁元月.提高SIFT特征匹配效率的方法研究[J].机械科学与技术，2009（9）:1252-1255.

[15]何斌，马天予.数字图像处理[M].北京:人民邮电出版社，2002.

Based on the improved SIFT algorithm of image registration

DU Yi-rong
（College of Information Engineering，Dalian University，Dalian 116622，China）

Aiming at the problem of Scale Invariant Feature Transform（SIFT）achieving low matching rate when registrating images，an image registration method based on improved SIFT is proposed.This paper mainly discusses the image gradient sharpening processing，to highlight the edge，reuse SIFT algorithm to extract key point；and match sharpened images.to complete the image registration.The experimental results show that the method of matching result is superior to SIFT method，and the matching rate is higher than the traditional SIFT algorithm.

image registration；SIFT；gradient sharpening；key point extraction；matching ratio

TN911.73

：A

：1674－6236（2017）06-0185-05

2016-03-23稿件编号：201603318

杜以荣（1990—），女，山东临沂人，硕士研究生。研究方向：图像配准。